DOCSLIB.ORG

Fx-991EX Learning Mathematics with Classwiz.Pdf

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Fx-991EX Learning Mathematics with Classwiz.Pdf PREFACE Over 40 years, the scientific calculator has evolved from being a computational device for scientists and engineers to becoming an important educational tool. What began as an instrument to answer numerical questions has evolved to become an affordable, powerful and flexible environment for students and their teachers to explore a wide range of mathematical ideas and relationships. The significant calculator developments of recent years, together with advice from experienced teachers, have culminated in the advanced scientific calculators, the CASIO fx-991 EX and the CASIO fx-570 EX, with substantial mathematical capabilities, including a spreadsheet, and extensive use of natural displays of mathematical notation. This publication comprises a series of modules to help make best use of the opportunities for mathematics education afforded by these developments. The focus of the modules is on the use of the ClassWiz in the development of students’ understanding of mathematical concepts and relationships, as an integral part of the development of mathematical meaning for the students. While meeting the computational needs of students throughout secondary school, and beyond, the ClassWiz can also be used to advantage by students to support their initial learning of the mathematical ideas involved; the calculator is not only a device to be used to undertake or to check computations, after the mathematics has been understood. The mathematics involved in the modules spans a wide range from the early years of secondary school to the early undergraduate years, from early ideas of number and algebra through to the study of calculus, probability and statistics, as well as advanced topics such as vectors, matrices and complex numbers. I expect that readers will decide which modules suit their purposes. Although mathematics curricula vary across different countries, I am confident that the mathematical ideas included in the modules will be of interest to mathematics teachers and their students across international boundaries. The text of each modules is intended to be read by both teachers and students, to understand how the ClassWiz is related to various aspects of mathematics, and also to help them to use it efficiently. Each module contains a set of Exercises, focusing on calculator skills relevant to the mathematics associated with the module. In addition, a set of exploratory Activities is provided for each module after the first, to illustrate some of the ways in which the calculator can be used to explore mathematical ideas through the use of the calculator; these are not intended to be exhaustive, and I expect that teachers will develop further activities of these kinds to suit their students. The Notes for Teachers in each module provide answers to exercises, as well as some advice about the classroom use of the activities (including answers where appropriate). Permission is given for the reproduction of any of the materials for educational purposes. The material in many of these modules draws significantly on materials developed earlier by Marian Kemp and myself, refining and extending those materials to take advantage of the many innovative features included in the ClassWiz. I am grateful to CASIO for supporting the development of these materials, and appreciate in particular the assistance of Mr Yoshino throughout the developmental process, as well as the careful proof-reading of Mr Rabieh Al Halabi. I hope that users of these materials enjoy working with the calculator as much as I have enjoyed developing the materials and I wish both teachers and their students a productive engagement with mathematics through the use of the ClassWiz. Barry Kissane Murdoch University, Western Australia Table of Contents Module 1: Introduction to ClassWiz ········································································ 1 Entering and editing commands ········································································ 1 Mathematical commands ················································································ 2 Recalling commands ····················································································· 4 Scientific and engineering notation ···································································· 5 Calculator modes ························································································· 7 OPTN commands ························································································· 8 SET UP ···································································································· 8 Memories ································································································ 12 Initializing the calculator ·············································································· 13 Exercises and Notes for teachers ····································································· 14 Module 2: Representing numbers ········································································· 16 Representing decimals ················································································· 16 Representing fractions ················································································· 17 Representing percentages ·············································································· 18 Recurring decimals ····················································································· 18 Powers ···································································································· 20 Factors ···································································································· 22 Scientific notation ······················································································ 23 Roots ····································································································· 24 Reciprocals ······························································································ 25 Rational and irrational numbers ······································································ 26 Exercises, Activities and Notes for teachers ························································ 28 Module 3: Functions ························································································· 31 Evaluating expressions and functions ································································ 31 Comparing expressions ················································································ 32 Using tables of values ·················································································· 32 Linear and quadratic functions ········································································ 34 Cubic functions ························································································· 36 Reciprocal functions ···················································································· 37 Maximum and minimum values ······································································ 39 Intersection of two graphs ············································································· 40 Exercises, Activities and Notes for teachers ························································ 42 i Module 4: Equations and inequalities ···································································· 45 Equations, inequalities and a table ··································································· 45 Using two tables ························································································ 47 Automatic equation solving ··········································································· 48 Automatic inequality solving ·········································································· 49 Solving quadratic equations and inequalities ······················································· 50 Systems of linear equations ··········································································· 51 Using the Solver ························································································ 52 Ratio and proportion ··················································································· 55 Exercises, Activities and Notes for teachers ························································ 57 Module 5: Trigonometry ···················································································· 60 Trigonometry and right triangles ····································································· 60 Tables of values ························································································· 62 Exact values ····························································································· 63 Radian measure ························································································· 64 Gradian measure ························································································ 65 Solving triangles with the Sine Rule ································································· 66 Solving triangles with the Cosine Rule ······························································ 67 The Pythagorean Identity ·············································································· 68 Coordinate systems ····················································································· 69 Trigonometric equations ··············································································· 70 Exercises,
Load more

Recommended publications
  • Implementation and Design of Calculator
    Implementation and Design of Calculator Submitted To: Sir. Muhammad Abdullah Submitted By: Muhammad Huzaifa Bashir 2013-EE-125 Department of Electrical Engineering University of Engineering and Technology, Lahore Contents Abstract ........................................................................................................................................... 2 Introduction ..................................................................................................................................... 3 Input Unit: ................................................................................................................................... 3 Processing Unit: .......................................................................................................................... 3 Output Unit: ................................................................................................................................ 3 Interfacing and Implementation ...................................................................................................... 4 LCD: ........................................................................................................................................... 4 Hardware Interfacing: ............................................................................................................. 4 Problem and Solution of hardware interfacing: ...................................................................... 4 Software Interfacing: .............................................................................................................
    [Show full text]
  • Computing Systems
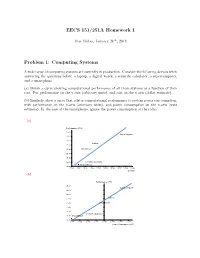
    EECS 151/251A Homework 1 Due Friday, January 26th, 2018 Problem 1: Computing Systems A wide range of computing systems are currently in production. Consider the following devices when answering the questions below: a laptop, a digital watch, a scientific calculator, a supercomputer, and a smartphone. (a) Sketch a curve showing computational performance of all these systems as a function of their cost. Put performance on the y-axis (arbitrary units), and cost on the x-axis (dollar estimate). (b) Similarly, show a curve that relates computational performance to system power con- sumption, with performance on the y-axis (arbitrary units), and power consumption on the x-axis (watt estimate). In the case of the smartphone, ignore the power consumption of the radio. (a) Performance (IPS)! 1.E+16! Supercomputer! 1.E+14! 1.E+12! Laptop! 1.E+10! 1.E+08! Smartphone! 1.E+06! 1.E+04! 1.E+02! Scientific Calculator! Digital Watch! 1.E+00! 1.E+00! 1.E+01! 1.E+02! 1.E+03! 1.E+04! 1.E+05! 1.E+06! 1.E+07! 1.E+08! 1.E+09! Cost ($)! (b) Performance (IPS)! 1.E+16! Supercomputer! 1.E+14! 1.E+12! Laptop! 1.E+10! 1.E+08! Smartphone! 1.E+06! 1.E+04! Scientific Calculator! 1.E+02! Digital Watch! 1.E+00! 1.E-08! 1.E-06! 1.E-04! 1.E-02! 1.E+00! 1.E+02! 1.E+04! 1.E+06! Power Consumption (W)! EECS 151/251A Homework 1 2 Problem 2: Logic Consider the circuit below.
    [Show full text]
  • Samsung Galaxy J3 V J327V User Manual
    User guide. User guide. User usuario. Guía del Guía GH68-47432D Printed in USA Galaxy J7_COLL-78600-UG-PO-CVR-6x4-V3-F-R2R.indd All Pages 2/2/17 11:00 AM SMARTPHONE User Manual Please read this manual before operating your device and keep it for future reference. Table of Contents Special Features . 1 Navigation . 28 Side Speaker . 2 Entering Text . 30 Getting Started . 3 Multi Window . 33 Set Up Your Device . 4. Emergency Mode . 35 Assemble Your Device . .5 Apps . 37 Start Using Your Device . 10 Using Apps . 38 Set Up Your Device . 11 Applications Settings . 41 Learn About Your Device . .15 Calculator . 45 Front View . 16 Calendar . 46 Back View . .18 Camera and Video . 49 Home Screen . .19 Clock . 54 VZW_J727V_EN_UM_TN_QB1_031717_FINAL Contacts . 57 Connections . 104 Email . 64 Wi‑Fi . 105 Gallery . .67 Bluetooth . 108 Google Apps . 71 Data Usage . 111 Message+ . .74 Airplane Mode . 113 Messages . .77 Mobile Hotspot . .114 My Files . 82 Tethering . 117 Phone . 84 Mobile Networks . 117 S Health . 94 Location . 118 Samsung Gear . 96 Advanced Calling . .119 Samsung Notes . 97 Nearby Device Scanning . .121 Verizon Apps . 99 Phone Visibility . .121 Settings . 101 Printing . .121 How to Use Settings . 102 Virtual Private Networks (VPN) . .121 Change Carrier . 123 Table of Contents iii Data Plan . 123 Smart Alert . 133 Sounds and Vibration . 124 Display . 134 Sound Mode . 125 Screen Brightness . 135 Easy Mute . 125 Screen Zoom and Font . 135 Vibrations . 125 Home Screen . 136 Volume . 126. Easy Mode . 136 Ringtone . .127 Icon Frames . .137 Notification Sounds . 128 Status Bar . .137 Do Not Disturb . 128 Screen Timeout .
    [Show full text]
  • Calculating Solutions Powered by HP Learn More
    Issue 29, October 2012 Calculating solutions powered by HP These donations will go towards the advancement of education solutions for students worldwide. Learn more Gary Tenzer, a real estate investment banker from Los Angeles, has used HP calculators throughout his career in and outside of the office. Customer corner Richard J. Nelson Learn about what was discussed at the 39th Hewlett-Packard Handheld Conference (HHC) dedicated to HP calculators, held in Nashville, TN on September 22-23, 2012. Read more Palmer Hanson By using previously published data on calculating the digits of Pi, Palmer describes how this data is fit using a power function fit, linear fit and a weighted data power function fit. Check it out Richard J. Nelson Explore nine examples of measuring the current drawn by a calculator--a difficult measurement because of the requirement of inserting a meter into the power supply circuit. Learn more Namir Shammas Learn about the HP models that provide solver support and the scan range method of a multi-root solver. Read more Learn more about current articles and feedback from the latest Solve newsletter including a new One Minute Marvels and HP user community news. Read more Richard J. Nelson What do solutions of third degree equations, electrical impedance, electro-magnetic fields, light beams, and the imaginary unit have in common? Find out in this month's math review series. Explore now Welcome to the twenty-ninth edition of the HP Solve Download the PDF newsletter. Learn calculation concepts, get advice to help you version of articles succeed in the office or the classroom, and be the first to find out about new HP calculating solutions and special offers.
    [Show full text]
  • Numeration 2016
    Numeration 2016 Prague, Czech Republic, May 23–27 2016 Department of Mathematics FNSPE Czech Technical University in Prague Numeration 2016 Prague, Czech Republic, May 23–27 2016 Department of Mathematics FNSPE Czech Technical University in Prague Print: Česká technika — nakladatelství ČVUT Editor: Petr Ambrož [email protected] Katedra matematiky Fakulta jaderná a fyzikálně inženýrská České vysoké učení technické v Praze Trojanova 13 120 00 Praha 2 List of Participants Rafael Alcaraz Barrera [email protected] IME, University of São Paulo Karam Aloui [email protected] Institut Elie Cartan de Nancy / Faculté des Sciences de Sfax Petr Ambrož petr.ambroz@fjfi.cvut.cz FNSPE, Czech Technical University in Prague Hamdi Ammar [email protected] Sfax University Myriam Amri [email protected] Sfax University Hamdi Aouinti [email protected] Université de Tunis Simon Baker [email protected] University of Reading Christoph Bandt [email protected] University of Greifswald Attila Bérczes [email protected] University of Debrecen Anne Bertrand-Mathis [email protected] University of Poitiers Dávid Bóka [email protected] Eötvös Loránd University Horst Brunotte [email protected] Marta Brzicová [email protected] FNSPE, Czech Technical University in Prague Péter Burcsi [email protected] Eötvös Loránd University Francesco Dolce [email protected] Université Paris-Est Art¯urasDubickas [email protected] Vilnius University Lubomira Dvořáková [email protected] FNSPE, Czech
    [Show full text]
  • Residue Arithmetic in Digital Computers
    r* 6 l't ¡r "RESIDUT ARITHMETIC IN DIGITAL COIIPUTERS" RAMESH CHANDRA DEBNATH/ M.SC. BEING A THESIS SUBMITTED FOR THE DEGREE OF DOCTOR OF PHILOSOPHY IN THE DEPARTMENT OF ELECTRICAL ENGINEERING THE UNIVERSITY OF ADELAIDE IVIARCl-i I979 SUIq¡4ARY The number systems used have great impact on the speed of a computer, At present at least 4 number systems (binary, negabinary, ternary and residue) are in use either for general purposes or for special purposes. The calîry plîopagation delay which j-s inherent to all weighted systems (binary, negabi-nary and ternary) is a limiting factor on the speed of computations. tlnlike the weighted system, the residue system is carry free which is the m¿rln attractj-ve feature of this system and therefore its potentiality in a general purpose computer, in the light of present day tech- nology, has been investigated. As the background of the investigation the binary and negabinary arithmetic have been thoroughly studied. A ne',r method for fractional negabinary division, and a correction on negabinary multiplì-cation have been proposed. It has been observed that the binary arithmetic operations are fas- ter thair thcse ir. negabinary syslem. The residue system has got. problems too. The sign detectj-on, operations j-nvolving sign detection (comparison, overflow detection, division) and the resj-due-to--decimal- con- version are difficult. Moreover, the residue systemT being an i.nteger: systetn, makes floati-ng poinc arithmetic operatlcns very difficult. The def:ails of the existing algorithms,/ methods to solve those problems have been thoroughly inves- tigated and drawbacks of those algoritlrms/methods have been di scussed.
    [Show full text]
  • Calculator Policy
    CALCULATOR POLICY 1. Examination Candidates may take a non-programmable calculator into any component of the examination for their personal use. 2. Instruction booklets or cards (eg reference cards) on the operation of calculators are NOT permitted in the examination room. Candidates are expected to familiarise themselves with the calculator’s operation beforehand. 3. Calculators must have been switched off for entry into the examination room. 4. Calculators will be checked for compliance with this policy by the examination invigilator or observer. 5. Features of approved calculators: 5.1. In addition to the features of a basic (four operation) calculator, a scientific calculator typically includes the following: 5.1.1. fraction keys (for fraction arithmetic) 5.1.2. a percentage key 5.1.3. a π key 5.1.4. memory access keys 5.1.5. an EXP key and a sign change (+/-) key 5.1.6. square (x²) and square root (√) keys 5.1.7. logarithm and exponential keys (base 10 and base e) 5.1.8. a power key (ax, xy or similar) 5.1.9. trigonometrical function keys with an INVERSE key for the inverse functions 5.1.10. a capacity to work in both degree and radian mode 5.1.11. a reciprocal key (1/x) 5.1.12. permutation and/or combination keys ( nPr , nCr ) 5.1.13. cube and/or cube root keys 5.1.14. parentheses keys 5.1.15. statistical operations such as mean and standard deviation 5.1.16. metric or currency conversion 6. Features of calculators that are NOT permitted include: 6.1.
    [Show full text]
  • **4************ from the Original Document
    DoCUMENT/ RESUME ED 220 67)9 CE 033 642 TITLE Military Curriculum Materials for Vocational and (14Technical Educaticin. Fundamentals of Digital Logic, 7-1. INSTITUTION Marine Corps, Washington, D.C.; Ohio State Univ., Columbus. National Center for Research in Vocational Education, SPONS AGENCY Office of Education (DHEW), Washington, D.C4. PUB DATE (76) NOTE 146p. EDR's PRICE MF01/P606 PlusPostase. DESCRIPTORS Arithmetic; *Digital'IComputers; *Electric Circuits; *Electronic Technicians; !Equipment Maintenance; Individualized Instruction; Instructional Materials; *Mathematical Lpgic; Mathematics; Military Personnel; Military TrainVng; Postsecondary Educationp Secondary Education; *Technical Education IDENTIFIERS Binary Arithmetic; Boolean Algebra; *Computer Logic; Military Curriculum Project ABSTRACT 'Tarqeted for grades0'through adult, these military-developed curriculum mater als consist ofa student lesson book with text readings and review pierVes designed to prepare electronic.per,sonnel for further trainin in digital'techniques. Covered,in the five lessons are binary arithmeti8 (number systems, decimal systemi, the mathematical form of notation, number system conversion, matheinatical operat4ons, specially coded systems); Boolean.a,lgebra (basic 'functions, signal levels, application of L Boolean algebra, Boolean equations, drawing logic diagrams, theorems and truth tables, simplifying Boolean equations); logic gates (diode logic circuits, transistor logic ,ci.rcuits, NOT circuits, EXCLUSIVE OR circu0s, operational analysis); logic
    [Show full text]
  • The Demise of the Slide Rule (And the Advent of Its Successors)
    OEVP/27-12-2002 The Demise of the Slide Rule (and the advent of its successors) Every text on slide rules describes in a last paragraph, sadly, that the demise of the slide rule was caused by the advent of the electronic pocket calculator. But what happened exactly at this turning point in the history of calculating instruments, and does the slide rule "aficionado" have a real cause for sadness over these events? For an adequate treatment of such questions, it is useful to consider in more detail some aspects like the actual usage of the slide rule, the performance of calculating instruments and the evolution of electronic calculators. Usage of Slide Rules During the first half of the 20th century, both slide rules and mechanical calculators were commercially available, mass-produced and at a reasonable price. The slide rule was very portable ("palmtop" in current speak, but without the batteries), could do transcendental functions like sine and logarithms (besides the basic multiplication and division), but required a certain understanding by the user. Ordinary people did not know how to use it straight away. The owner therefore derived from his knowledge a certain status, to be shown with a quick "what-if" calculation, out of his shirt pocket. The mechanical calculator, on the other hand, was large and heavy ("desktop" format), and had addition and subtraction as basic functions. Also multiplication and division were possible, in most cases as repeated addition or subtraction, although there were models (like the Millionaire) that could execute multiplications directly. For mechanical calculators there was no real equivalent of the profession-specific slide rule (e.g.
    [Show full text]
  • Appendix: the Cost of Computing: Big-O and Recursion
    Appendix: The Cost of Computing: Big-O and Recursion Big-O otation In the previous section we have seen a chart comparing execution times for various sorting algorithms. The chart, however, did not show any absolute numbers to tell us the actual time it took, say, to sort an array of 10,000 double numbers using the insertion sort algorithm. That is because the actual time depends, among other things, on the processor of the machine the program is running on, not only on the algorithm used. For example, the worst possible sorting algorithm executing on a Pentium II 450 MHz chip may finish a lot quicker in some situations than the best possible sorting algorithm running on an old Intel 386 chip. Even when two algorithms execute on the same machine, other processes that are running on the system can considerably skew the results one way or another. Therefore, execution time is not really an adequate measurement of the "goodness" of an algorithm. We need a more mathematical way to determine how good an algorithm is, and which of two algorithms is better. In this section, we will introduce the "big-O" notation, which does provide just that: a mathematical description that allows you to rate an algorithm. The Math behind Big-O There is a little background mathematics required to work with this concept, but it is not much, and you should quickly understand the major concepts involved. The most important concept you may need to review is that of the limit of a function. Definition: Limit of a Function We say that a function f converges to a limit L as x approaches a number c if f(x) gets closer and closer to L if x gets closer and closer to c, and we use the notation lim f (x) = L x→c Similarly, a function f converges to a limit L as x approaches positive (negative) infinity if f(x) gets closer and closer to L as x is positive (negative) and gets bigger (smaller) and bigger (smaller).
    [Show full text]
  • Scale Drawings, Similar Figures, Right Triangle Trigonometry
    SCALE DRAWINGS, SIMILAR FIGURES, RIGHT TRIANGLE TRIGONOMETRY In this unit, you will review ratio and proportion and solve problems related to scale drawings and similar figures. You will then investigate right triangle trigonometry. You will examine how trigonometry is derived from the angles and sides of right triangles and then apply “trig” functions to solve problems. Proportions Applications of Proportions Scale Drawings and Map Distances Similar Polygons Trigonometric Ratios Table of Trigonometric Ratios Map of Ohio Proportions A ratio is a comparison of two quantities and is often written as a fraction. For example, Emily is on the basketball team and during her first game she made 14 out of 20 shots. You can make a ratio out of shots made and shots attempted. shots made 14 7 == shots attempted 20 10 A proportion is any statement that two ratios are equal. For example, if Rachel is on the same basketball team as Emily, and she made 21 out of 30 baskets, Rachel’s ratio can be written as: shots made 21 7 == shots attempted 30 10 14 21 It can now be said that Emily’s ratio and Rachel’s ratio are equal. To prove this 20 30 we will use the “cross products property”. For all real numbers a, b, c, and d, where b ≠ 0 and d ≠ 0 . ac = if ad= bc bd Let’s take a look at Emily and Rachel’s ratios and use the cross product property to make sure they are equal. 14 21 = 20 30 14×=× 30 20 21 420= 420 true Use cross products to determine if the two ratios are proportional.
    [Show full text]
  • On Expansions in Non-Integer Base
    SAPIENZA UNIVERSITA` DI ROMA DOTTORATO DI RICERCA IN “MODELLI E METODI MATEMATICI PER LA TECNOLOGIA E LA SOCIETA` ” XXII CICLO AND UNIVERSITE´ PARIS 7-PARIS DIDEROT DOCTORAT D’INFORMATIQUE On expansions in non-integer base Anna Chiara Lai Dipartimento di Metodi e Modelli Matematici per le Scienze applicate Via Antonio Scarpa, 16 - 00161 Roma. and Laboratoire d’Informatique Algorithmique: Fondements et Applications CNRS UMR 7089, Universit´eParis Diderot - Paris 7, Case 7014 75205 Paris Cedex 13 A. A. 2008-2009 Contents Introduction 3 Chapter 1. Background results on expansions in non-integer base 6 1. Our toolbox 6 2. Positional number systems 10 3. Positional numeration systems with positive integer base 11 4. Expansions in non-integer bases 12 Chapter 2. Expansions in complex base 17 1. Introduction 17 2. Geometrical background 18 3. Characterization of the convex hull of representable numbers 24 4. Representability in complex base 35 5. Overview of original contributions, conclusions and further developments 37 Chapter 3. Expansions in negative base 40 1. Introduction 40 2. Preliminaries on expansions in non-integer negative base 41 3. Symbolic dynamical systems and the alternate order 44 4. A characterization of sofic ( q)-shifts and ( q)-shifts of finite type 46 − − 5. Entropy of the ( q)-shift 47 − 6. The Pisot case 49 7. A conversion algorithm from positive to negative base 52 8. Overview of original contributions, conclusions and further developments 56 Chapter4. GeneralizedGoldenMeanforternaryalphabets 58 1. Introduction 58 2. Expansions in non-integer base with alphabet with deleted digits 58 3. Critical bases 60 4. Normal ternary alphabets 62 5.
    [Show full text]