The Demise of the Slide Rule (And the Advent of Its Successors)
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Implementation and Design of Calculator
Implementation and Design of Calculator Submitted To: Sir. Muhammad Abdullah Submitted By: Muhammad Huzaifa Bashir 2013-EE-125 Department of Electrical Engineering University of Engineering and Technology, Lahore Contents Abstract ........................................................................................................................................... 2 Introduction ..................................................................................................................................... 3 Input Unit: ................................................................................................................................... 3 Processing Unit: .......................................................................................................................... 3 Output Unit: ................................................................................................................................ 3 Interfacing and Implementation ...................................................................................................... 4 LCD: ........................................................................................................................................... 4 Hardware Interfacing: ............................................................................................................. 4 Problem and Solution of hardware interfacing: ...................................................................... 4 Software Interfacing: ............................................................................................................. -
Computing Systems
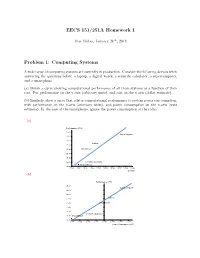
EECS 151/251A Homework 1 Due Friday, January 26th, 2018 Problem 1: Computing Systems A wide range of computing systems are currently in production. Consider the following devices when answering the questions below: a laptop, a digital watch, a scientific calculator, a supercomputer, and a smartphone. (a) Sketch a curve showing computational performance of all these systems as a function of their cost. Put performance on the y-axis (arbitrary units), and cost on the x-axis (dollar estimate). (b) Similarly, show a curve that relates computational performance to system power con- sumption, with performance on the y-axis (arbitrary units), and power consumption on the x-axis (watt estimate). In the case of the smartphone, ignore the power consumption of the radio. (a) Performance (IPS)! 1.E+16! Supercomputer! 1.E+14! 1.E+12! Laptop! 1.E+10! 1.E+08! Smartphone! 1.E+06! 1.E+04! 1.E+02! Scientific Calculator! Digital Watch! 1.E+00! 1.E+00! 1.E+01! 1.E+02! 1.E+03! 1.E+04! 1.E+05! 1.E+06! 1.E+07! 1.E+08! 1.E+09! Cost ($)! (b) Performance (IPS)! 1.E+16! Supercomputer! 1.E+14! 1.E+12! Laptop! 1.E+10! 1.E+08! Smartphone! 1.E+06! 1.E+04! Scientific Calculator! 1.E+02! Digital Watch! 1.E+00! 1.E-08! 1.E-06! 1.E-04! 1.E-02! 1.E+00! 1.E+02! 1.E+04! 1.E+06! Power Consumption (W)! EECS 151/251A Homework 1 2 Problem 2: Logic Consider the circuit below. -

Samsung Galaxy J3 V J327V User Manual
User guide. User guide. User usuario. Guía del Guía GH68-47432D Printed in USA Galaxy J7_COLL-78600-UG-PO-CVR-6x4-V3-F-R2R.indd All Pages 2/2/17 11:00 AM SMARTPHONE User Manual Please read this manual before operating your device and keep it for future reference. Table of Contents Special Features . 1 Navigation . 28 Side Speaker . 2 Entering Text . 30 Getting Started . 3 Multi Window . 33 Set Up Your Device . 4. Emergency Mode . 35 Assemble Your Device . .5 Apps . 37 Start Using Your Device . 10 Using Apps . 38 Set Up Your Device . 11 Applications Settings . 41 Learn About Your Device . .15 Calculator . 45 Front View . 16 Calendar . 46 Back View . .18 Camera and Video . 49 Home Screen . .19 Clock . 54 VZW_J727V_EN_UM_TN_QB1_031717_FINAL Contacts . 57 Connections . 104 Email . 64 Wi‑Fi . 105 Gallery . .67 Bluetooth . 108 Google Apps . 71 Data Usage . 111 Message+ . .74 Airplane Mode . 113 Messages . .77 Mobile Hotspot . .114 My Files . 82 Tethering . 117 Phone . 84 Mobile Networks . 117 S Health . 94 Location . 118 Samsung Gear . 96 Advanced Calling . .119 Samsung Notes . 97 Nearby Device Scanning . .121 Verizon Apps . 99 Phone Visibility . .121 Settings . 101 Printing . .121 How to Use Settings . 102 Virtual Private Networks (VPN) . .121 Change Carrier . 123 Table of Contents iii Data Plan . 123 Smart Alert . 133 Sounds and Vibration . 124 Display . 134 Sound Mode . 125 Screen Brightness . 135 Easy Mute . 125 Screen Zoom and Font . 135 Vibrations . 125 Home Screen . 136 Volume . 126. Easy Mode . 136 Ringtone . .127 Icon Frames . .137 Notification Sounds . 128 Status Bar . .137 Do Not Disturb . 128 Screen Timeout . -
Calculating Solutions Powered by HP Learn More
Issue 29, October 2012 Calculating solutions powered by HP These donations will go towards the advancement of education solutions for students worldwide. Learn more Gary Tenzer, a real estate investment banker from Los Angeles, has used HP calculators throughout his career in and outside of the office. Customer corner Richard J. Nelson Learn about what was discussed at the 39th Hewlett-Packard Handheld Conference (HHC) dedicated to HP calculators, held in Nashville, TN on September 22-23, 2012. Read more Palmer Hanson By using previously published data on calculating the digits of Pi, Palmer describes how this data is fit using a power function fit, linear fit and a weighted data power function fit. Check it out Richard J. Nelson Explore nine examples of measuring the current drawn by a calculator--a difficult measurement because of the requirement of inserting a meter into the power supply circuit. Learn more Namir Shammas Learn about the HP models that provide solver support and the scan range method of a multi-root solver. Read more Learn more about current articles and feedback from the latest Solve newsletter including a new One Minute Marvels and HP user community news. Read more Richard J. Nelson What do solutions of third degree equations, electrical impedance, electro-magnetic fields, light beams, and the imaginary unit have in common? Find out in this month's math review series. Explore now Welcome to the twenty-ninth edition of the HP Solve Download the PDF newsletter. Learn calculation concepts, get advice to help you version of articles succeed in the office or the classroom, and be the first to find out about new HP calculating solutions and special offers. -

Slide Rules: How Quickly We Forget Charles Molían If You Have Not Thrown out Your Old Slide Rule, Treasure It, Especially If It Is One of the More Sophisticated Types
HISTORY OF PHYSICS91 Instrumental Background Slide Rules: How Quickly We Forget Charles Molían If you have not thrown out your old slide rule, treasure it, especially if it is one of the more sophisticated types. It is a relic of a recent age In 1614 John Napier published details of invention of the electronic calculator. Fig 1 top A straight slide rule from A.W. Faber of Bavaria his logarithms which reduced multiplica The bigger the slide rule, the more cl 905. (The illustration is from a 1911 catalogue). In this engraving the number 1 on the bottom scale of the slide tion and division to simple addition and accurate the calculations. But there are is placed above 1.26 on the lower scale on the main body subtraction. To make logarithms easier he limits to practicable lengths so various of the rule. The number 2 on the slide corresponds to devised rectangular rods inscribed with ingenious people devised ways of increas 2.52 on the lower scale, the number 4 to 5.04, and any numbers which became known as ing the scale while maintaining the device other number gives a multiple of 1.26. The line on the ‘Napier’s Bones’. By 1620, Edmund Gunter at a workable size. Several of these slide transparent cursor is at 4.1, giving the result of the had devised his ‘Gunter scale’, or Tine of rules became fairly popular, and included multiplication 1.26 x 4.1 as 5.15 (it should be 5.17 but the engraving is a little out).The longer the slide rule and numbers’, a plot of logarithms on a line. -

The Concise Stadia Computer, Or the Text Printed on the Instrument Itself, Or Any Other Documentation Prepared by Concise for This Instrument
Copyright. © 2005 by Steven C. Beadle (scbead 1e @ earth1ink.net). Permission is hereby granted to the members of the International Slide Rule Group (ISRG; http://groups.yahoo.com/group/sliderule) and the Slide Rule Trading Group (SRTG; http://groups.yahoo.com/group/sliderule-trade) to make unlimited copies of this doc- ument, in either electronic or printed format, for their personal use. Commercial redistribution, without the written permission of the copyright holder, is prohibited. THE CONCISE Disclaimer. This document is an independently written guide for the Concise STADIA Stadia Computer, a product of the Concise Co. Ltd., located at 2-16-23, Hirai, Edogawa-ku, Tokyo, Japan (“Concise”). This guide was prepared without the authori- zation, consent, or cooperation of Concise. The copyright holder, and not Concise or COMPUTER the ISRG, is responsible for any errors or omissions. This document was developed without translation of the Japanese language manual Herman van Herwijnen for the Concise Stadia Computer, or the text printed on the instrument itself, or any other documentation prepared by Concise for this instrument. Thus, there is no Memorial Edition assurance that the guidance presented in this document accurately reflects the uses of this instrument as intended by the manufacturer, or that it offers an accurate inter- pretation of the scales, labels, tables, and other features of this instrument. The interpretations presented in this document are distributed in the hope that they may be useful to English-speaking users of the Concise Stadia Computer. However, the copyright holder and the ISRG provide the document “as is” without warranty of any kind, either expressed or implied, including, but not limited to, the implied warranties of merchantability and fitness for a particular purpose. -

Calculator Policy
CALCULATOR POLICY 1. Examination Candidates may take a non-programmable calculator into any component of the examination for their personal use. 2. Instruction booklets or cards (eg reference cards) on the operation of calculators are NOT permitted in the examination room. Candidates are expected to familiarise themselves with the calculator’s operation beforehand. 3. Calculators must have been switched off for entry into the examination room. 4. Calculators will be checked for compliance with this policy by the examination invigilator or observer. 5. Features of approved calculators: 5.1. In addition to the features of a basic (four operation) calculator, a scientific calculator typically includes the following: 5.1.1. fraction keys (for fraction arithmetic) 5.1.2. a percentage key 5.1.3. a π key 5.1.4. memory access keys 5.1.5. an EXP key and a sign change (+/-) key 5.1.6. square (x²) and square root (√) keys 5.1.7. logarithm and exponential keys (base 10 and base e) 5.1.8. a power key (ax, xy or similar) 5.1.9. trigonometrical function keys with an INVERSE key for the inverse functions 5.1.10. a capacity to work in both degree and radian mode 5.1.11. a reciprocal key (1/x) 5.1.12. permutation and/or combination keys ( nPr , nCr ) 5.1.13. cube and/or cube root keys 5.1.14. parentheses keys 5.1.15. statistical operations such as mean and standard deviation 5.1.16. metric or currency conversion 6. Features of calculators that are NOT permitted include: 6.1. -

Scale Drawings, Similar Figures, Right Triangle Trigonometry
SCALE DRAWINGS, SIMILAR FIGURES, RIGHT TRIANGLE TRIGONOMETRY In this unit, you will review ratio and proportion and solve problems related to scale drawings and similar figures. You will then investigate right triangle trigonometry. You will examine how trigonometry is derived from the angles and sides of right triangles and then apply “trig” functions to solve problems. Proportions Applications of Proportions Scale Drawings and Map Distances Similar Polygons Trigonometric Ratios Table of Trigonometric Ratios Map of Ohio Proportions A ratio is a comparison of two quantities and is often written as a fraction. For example, Emily is on the basketball team and during her first game she made 14 out of 20 shots. You can make a ratio out of shots made and shots attempted. shots made 14 7 == shots attempted 20 10 A proportion is any statement that two ratios are equal. For example, if Rachel is on the same basketball team as Emily, and she made 21 out of 30 baskets, Rachel’s ratio can be written as: shots made 21 7 == shots attempted 30 10 14 21 It can now be said that Emily’s ratio and Rachel’s ratio are equal. To prove this 20 30 we will use the “cross products property”. For all real numbers a, b, c, and d, where b ≠ 0 and d ≠ 0 . ac = if ad= bc bd Let’s take a look at Emily and Rachel’s ratios and use the cross product property to make sure they are equal. 14 21 = 20 30 14×=× 30 20 21 420= 420 true Use cross products to determine if the two ratios are proportional. -

Fourier Analyzer and Two Fast-Transform Periph- Erals Adapt to a Wide Range of Applications
JUNE 1972 TT-PACKARD JOURNAL The ‘Powerful Pocketful’: an Electronic Calculator Challenges the Slide Rule This nine-ounce, battery-po wered scientific calcu- lator, small enough to fit in a shirt pocket, has log a rithmic, trigon ome tric, and exponen tia I functions and computes answers to IO significant digits. By Thomas M. Whitney, France Rod& and Chung C. Tung HEN AN ENGINEER OR SCIENTIST transcendental functions (that is, trigonometric, log- W NEEDS A QUICK ANSWER to a problem arithmic, exponential) or even square root. Second, that requires multiplication, division, or transcen- the HP-35 has a full two-hundred-decade range, al- dental functions, he usually reaches for his ever- lowing numbers from 10-” to 9.999999999 X lo+’’ present slide rule. Before long, to be represented in scientific however, that faithful ‘slip stick’ notation. Third, the HP-35 has may find itself retired. There’s five registers for storing con- now an electronic pocket cal- stants and results instead of just culator that produces those an- one or two, and four of these swers more easily, more quickly, registers are arranged to form and much more accurately. an operational stack, a feature Despite its small size, the new found in some computers but HP-35 is a powerful scientific rarely in calculators (see box, calculator. The initial goals set page 5). On page 7 are a few for its design were to build a examples of the complex prob- shirt-pocket-sized scientific cal- lems that can be solved with the culator with four-hour operation HP-35, from rechargeable batteries at a cost any laboratory and many Data Entry individuals could easily justify. -

Scientific Calculator Apps As Alternative Tool in Solving
INTERNATIONAL JOURNAL OF RESEARCH IN TECHNOLOGY AND MANAGEMENT (IJRTM) ISSN 2454-6240 www.ijrtm.com SCIENTIFIC CALCULATOR APPS AS ALTERNATIVE TOOL IN SOLVING TRIGONOMETRY PROBLEMS Maria Isabel Lucas, EdD, Pamantasan ng Lungsod ng Maynila, Manila, Philippines [email protected] ABSTRACT Mark Prensky (2001), the originator of the term digital The present 21st century students belong to the post- natives (Generation Y and Z) and digital immigrants, the millennial generation or Gen Z. They are considered predecessors of the millennials, cited that mathematics have to digital natives who have high penchant on ICT gadgets be reengineered to match the characteristics of the 21st century learners: particularly on smartphones which have already formed In math, for example, the debate must no longer be about part of their daily necessities. The teachers who are digital whether to use calculators and computers – they are a part of immigrants may capitalize this by integrating technology the Digital Natives‟ world – but rather how to use them to as a tool for teaching and learning to cater their learning instill the things that are useful to have internalized, from key needs and interests. Free applications are available both skills and concepts to the multiplication tables. We should be for android and iOS operating systems such as scientific focusing on “future math” – approximation, statistics, binary calculator apps. This study verifies whether the use of the thinking. (p.5) mobile application in computing Trigonometry problems is Practically, not all students in the local university where a good alternative to the commonly used handheld this study was conducted can afford to buy the commercial calculators using a quasi-experiment among 50 students of handheld calculator due to its relatively high cost. -

EL-531W Scientific Calculator Operation Guide
SSCCIIEENNTTIIFFIICC CCAALLCCUULLAATTOORR OOPPEERRAATTIIOONN GGUUIIDDEE <W Series> CO NTENTS HOW TO OPERATE Read Before Using Key layout/Reset switch 2 Display pattern 3 Display format 3 Exponent display 4 Angular unit 5 Function and Key Operation O N/O FF, entry correction keys 6 Data entry keys 7 Random key 8 Modify key 9 Basic arithmetic keys, parentheses 10 Percent 11 Inverse, square, cube, xth power of y, square root, cube root, xth root of y 12 10 to the power of x, common logarithm 13 e to the power of x, natural logarithm 14 Factorials 15 Permutations, combinations 16 Time calculation 17 Fractional calculations 18 Memory calculations ~ 19 Last answer memory 20 Trigonometric functions 21 Arc trigonometric functions 22 Hyperbolic functions 23 Coordinate conversion 24 Binary, pental, octal, decimal, and hexadecimal operations (N-base) 25 STATISTICS FUNCTION Data input and correction 26 “ANS” keys for 1-variable statistics 27 “ANS” keys for 2-variable statistics 31 1 H ow to O pe ra te ≈Read B efore Using≈ This operation guide has been written based on the EL-531W , EL-509W , and EL-531W H models. Some functions described here are not featured on other models. In addition, key operations and symbols on the display may differ according to the model. 1 . K E Y L AY O U T 2nd function key Pressing this key will enable the functions written in orange above the calculator buttons. ON/C, OFF key D irect function 2nd function <Power on> <Power off> W ritten in orange above the O N/C key Mode key This calculator can operate in three different modes as follows. -

PDF Full Text
Digital Signal Processing: A Computer Science Perspective Jonathan Y. Stein Copyright 2000 John Wiley & Sons, Inc. Print ISBN 0-471-29546-9 Online ISBN 0-471-20059-X 16 Function Evaluation Algorithms Commercially available DSP processors are designed to efficiently implement FIR, IIR, and FFT computations, but most neglect to provide facilities for other desirable functions, such as square roots and trigonometric functions. The software libraries that come with such chips do include such functions, but one often finds these general-purpose functions to be unsuitable for the application at hand. Thus the DSP programmer is compelled to enter the field of numerical approximation of elementary functions. This field boasts a vast literature, but only relatively little of it is directly applicable to DSP applications. As a simple but important example, consider a complex mixer of the type used to shift a signal in frequency (see Section 8.5). For every sample time t, we must generate both sin@,) and cos(wt,), which is difficult using the rather limited instruction set of a DSP processor. Lack of accuracy in the calculations will cause phase instabilities in the mixed signal, while loss of precision will cause its frequency to drift. Accurate values can be quickly retrieved from lookup tables, but such tables require large amounts of memory and the values can only be stored for specific arguments. General purpose approximations tend to be inefficient to implement on DSPs and may introduce intolerable inaccuracy. In this chapter we will specifically discuss sine and cosine generation, as well as rectangular to polar conversion (needed for demodulation), and the computation of arctangent, square roots, Puthagorean addition and loga- rithms.