Lectures on Applied Algebra II
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Group Developed Weighing Matrices∗
AUSTRALASIAN JOURNAL OF COMBINATORICS Volume 55 (2013), Pages 205–233 Group developed weighing matrices∗ K. T. Arasu Department of Mathematics & Statistics Wright State University 3640 Colonel Glenn Highway, Dayton, OH 45435 U.S.A. Jeffrey R. Hollon Department of Mathematics Sinclair Community College 444 W 3rd Street, Dayton, OH 45402 U.S.A. Abstract A weighing matrix is a square matrix whose entries are 1, 0 or −1,such that the matrix times its transpose is some integer multiple of the identity matrix. We examine the case where these matrices are said to be devel- oped by an abelian group. Through a combination of extending previous results and by giving explicit constructions we will answer the question of existence for 318 such matrices of order and weight both below 100. At the end, we are left with 98 open cases out of a possible 1,022. Further, some of the new results provide insight into the existence of matrices with larger weights and orders. 1 Introduction 1.1 Group Developed Weighing Matrices A weighing matrix W = W (n, k) is a square matrix, of order n, whose entries are in t the set wi,j ∈{−1, 0, +1}. This matrix satisfies WW = kIn, where t denotes the matrix transpose, k is a positive integer known as the weight, and In is the identity matrix of size n. Definition 1.1. Let G be a group of order n.Ann×n matrix A =(agh) indexed by the elements of the group G (such that g and h belong to G)issaidtobeG-developed if it satisfies the condition agh = ag+k,h+k for all g, h, k ∈ G. -
![Arxiv:1302.2015V2 [Cs.CG]](https://docslib.b-cdn.net/cover/6716/arxiv-1302-2015v2-cs-cg-226716.webp)
Arxiv:1302.2015V2 [Cs.CG]
MATHEMATICS OF COMPUTATION Volume 00, Number 0, Pages 000–000 S 0025-5718(XX)0000-0 PERSISTENCE MODULES: ALGEBRA AND ALGORITHMS PRIMOZ SKRABA Joˇzef Stefan Institute, Ljubljana, Slovenia Artificial Intelligence Laboratory, Joˇzef Stefan Institute, Jamova 39, 1000 Ljubljana, Slovenia MIKAEL VEJDEMO-JOHANSSON Corresponding author Formerly: School of Computer Science, University of St Andrews, Scotland Computer Vision and Active Perception Lab, KTH, Teknikringen 14, 100 44 Stockholm, Sweden Abstract. Persistent homology was shown by Zomorodian and Carlsson [35] to be homology of graded chain complexes with coefficients in the graded ring k[t]. As such, the behavior of persistence modules — graded modules over k[t] — is an important part in the analysis and computation of persistent homology. In this paper we present a number of facts about persistence modules; ranging from the well-known but under-utilized to the reconstruction of techniques to work in a purely algebraic approach to persistent homology. In particular, the results we present give concrete algorithms to compute the persistent homology of a simplicial complex with torsion in the chain complex. Contents 1. Introduction 2 2. Persistent (Co-)Homology 3 arXiv:1302.2015v2 [cs.CG] 15 Feb 2013 3. Overview of Commutative Algebra 4 4. Applications 21 5. Conclusions & Future Work 23 References 23 Appendix A. Algorithm for Computing Presentations of Persistence Modules 25 Appendix B. Relative Persistent Homology Example 26 E-mail addresses: [email protected], [email protected]. 2010 Mathematics Subject Classification. 13P10, 55N35. c XXXX American Mathematical Society 1 2 PERSISTENCE MODULES: ALGEBRA AND ALGORITHMS 1. Introduction The ideas of topological persistence [20] and persistent homology [35] have had a fundamental impact on computational geometry and the newly spawned field of applied topology. -

Operating Manual R&S NRP-Z22
Operating Manual Average Power Sensor R&S NRP-Z22 1137.7506.02 R&S NRP-Z23 1137.8002.02 R&S NRP-Z24 1137.8502.02 Test and Measurement 1137.7870.12-07- 1 Dear Customer, R&S® is a registered trademark of Rohde & Schwarz GmbH & Co. KG Trade names are trademarks of the owners. 1137.7870.12-07- 2 Basic Safety Instructions Always read through and comply with the following safety instructions! All plants and locations of the Rohde & Schwarz group of companies make every effort to keep the safety standards of our products up to date and to offer our customers the highest possible degree of safety. Our products and the auxiliary equipment they require are designed, built and tested in accordance with the safety standards that apply in each case. Compliance with these standards is continuously monitored by our quality assurance system. The product described here has been designed, built and tested in accordance with the EC Certificate of Conformity and has left the manufacturer’s plant in a condition fully complying with safety standards. To maintain this condition and to ensure safe operation, you must observe all instructions and warnings provided in this manual. If you have any questions regarding these safety instructions, the Rohde & Schwarz group of companies will be happy to answer them. Furthermore, it is your responsibility to use the product in an appropriate manner. This product is designed for use solely in industrial and laboratory environments or, if expressly permitted, also in the field and must not be used in any way that may cause personal injury or property damage. -

Z1 Z2 Z4 Z5 Z6 Z7 Z3 Z8
Illinois State Police Division of Criminal Investigation JO DAVIESS STEPHENSON WINNEBAGO B McHENRY LAKE DIVISION OF CRIMINAL INVESTIGATION - O O Colonel Mark R. Peyton Pecatonica 16 N E Chicago Lieutenant Colonel Chris Trame CARROLL OGLE Chief of Staff DE KALB KANE Elgin COOK Lieutenant Jonathan Edwards NORTH 2 Z1DU PAGE C WHITESIDE LEE 15 1 Z2 NORTH COMMAND - Sterling KENDALL WILL Major Michael Witt LA SALLE 5 Zone 1 - (Districts Chicago and 2) East Moline HENRY BUREAU Captain Matthew Gainer 7 17 Joliet ROCK ISLAND GRUNDY Zone 2 - (Districts 1, 7, 16) LaSalle MERCER Captain Christopher Endress KANKAKEE PUTNAM Z3 Zone 3 - (Districts 5, 17, 21) KNOX STARK Captain Richard Wilk H MARSHALL LIVINGSTON E WARREN Statewide Gaming Command IROQUOIS N PEORIA 6 Captain Sean Brannon D WOODFORD E Pontiac Ashkum CENTRAL R 8 Metamora S 21 O McLEAN N FULTON CENTRAL COMMAND - McDONOUGH HANCOCK TAZEWELL Captain Calvin Brown, Interim Macomb FORD VERMILION Zone 4 - (Districts 8, 9, 14, 20) 14 MASON CHAMPAIGN Captain Don Payton LOGAN DE WITT SCHUYLER Zone 5 - (Districts 6, 10) PIATT ADAMS Captain Jason Henderson MENARD Investigative Support Command CASS MACON Pesotum BROWN Captain Aaron Fullington Z4 10 SANGAMON Medicaid Fraud Control Bureau MORGAN DOUGLAS EDGAR PIKE 9 Z5 Captain William Langheim Pittsfield SCOTT MOULTRIE Springfield 20 CHRISTIAN COLES SHELBY GREENE MACOUPIN SOUTH COMMAND - CLARK Major William Sons C CUMBERLAND A MONTGOMERY L Zone 6 - (Districts 11, 18) H Litchfield 18 O Lieutenant Abigail Keller, Interim JERSEY FAYETTE EFFINGHAM JASPER U Zone 7 - (Districts 13, 22) N Effingham 12 CRAWFORD Z6 BOND Captain Nicholas Dill MADISON Zone 8 - (Districts 12, 19) CLAY Collinsville RICHLAND LAWRENCE Captain Ryan Shoemaker MARION 11 Special Operations Command ST. -
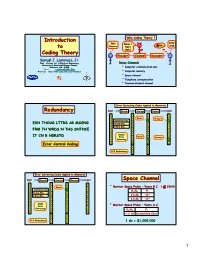
Introduction to Coding Theory
Introduction Why Coding Theory ? Introduction Info Info Noise ! Info »?# Sink to Source Heh ! Sink Heh ! Coding Theory Encoder Channel Decoder Samuel J. Lomonaco, Jr. Dept. of Comp. Sci. & Electrical Engineering Noisy Channels University of Maryland Baltimore County Baltimore, MD 21250 • Computer communication line Email: [email protected] WebPage: http://www.csee.umbc.edu/~lomonaco • Computer memory • Space channel • Telephone communication • Teacher/student channel Error Detecting Codes Applied to Memories Redundancy Input Encode Storage Detect Output 1 1 1 1 0 0 0 0 1 1 Error 1 Erasure 1 1 31=16+5 Code 1 0 ? 0 0 0 0 EVN THOUG LTTRS AR MSSNG 1 16 Info Bits 1 1 1 0 5 Red. Bits 0 0 0 0 0 0 0 FRM TH WRDS N THS SNTNCE 1 1 1 1 0 0 0 0 1 1 1 Double 1 IT CN B NDRSTD 0 0 0 0 1 Error 1 Error 1 Erasure 1 1 Detecting 1 0 ? 0 0 0 0 1 1 1 1 Error Control Coding 0 0 1 1 0 0 31% Redundancy 1 1 1 1 Error Correcting Codes Applied to Memories Input Encode Storage Correct Output Space Channel 1 1 1 1 0 0 0 0 Mariner Space Probe – Years B.C. ( ≤ 1964) 1 1 Error 1 1 • 1 31=16+5 Code 1 0 1 0 0 0 0 Eb/N0 Pe 16 Info Bits 1 1 1 1 -3 0 5 Red. Bits 0 0 0 6.8 db 10 0 0 0 0 -5 1 1 1 1 9.8 db 10 0 0 0 0 1 1 1 Single 1 0 0 0 0 Error 1 1 • Mariner Space Probe – Years A.C. -

ACM-8RF Connected to the EIA-485 Port
G PN 50362:C0 ECN 01-155 Control Relay Module ACM-8RF Instruction Manual Document 50362 03/21/2001 Rev: C While a fire alarm system may lower insurance Fire Alarm System Limitations rates, it is not a substitute for fire insurance! An automatic fire alarm system–typically made up Heat detectors do not sense particles of combustion of smoke detectors, heat detectors, manual pull and alarm only when heat on their sensors increases stations, audible warning devices, and a fire alarm at a predetermined rate or reaches a predetermined control with remote notification capability–can provide level. Rate-of-rise heat detectors may be subject to early warning of a developing fire. Such a system, reduced sensitivity over time. For this reason, the however, does not assure protection against property rate-of-rise feature of each detector should be tested damage or loss of life resulting from a fire. at least once per year by a qualified fire protection specialist. Heat detectors are designed to protect The Manufacturer recommends that smoke and/or property, not life. heat detectors be located throughout a protected premise following the recommendations of the current IMPORTANT! Smoke detectors must be installed in edition of the National Fire Protection Association the same room as the control panel and in rooms Standard 72 (NFPA 72), manufacturer's recommenda- used by the system for the connection of alarm tions, State and local codes, and the recommenda- transmission wiring, communications, signaling, and/or tions contained in the Guide for Proper Use of System power. If detectors are not so located, a developing Smoke Detectors, which is made available at no fire may damage the alarm system, crippling its ability charge to all installing dealers. -

Computer Simulation of an Unsprung Vehicle, Part I C
Agricultural and Biosystems Engineering Agricultural and Biosystems Engineering Publications 1967 Computer Simulation of an Unsprung Vehicle, Part I C. E. Goering University of Missouri Wesley F. Buchele Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/abe_eng_pubs Part of the Agriculture Commons, and the Bioresource and Agricultural Engineering Commons The ompc lete bibliographic information for this item can be found at https://lib.dr.iastate.edu/ abe_eng_pubs/960. For information on how to cite this item, please visit http://lib.dr.iastate.edu/ howtocite.html. This Article is brought to you for free and open access by the Agricultural and Biosystems Engineering at Iowa State University Digital Repository. It has been accepted for inclusion in Agricultural and Biosystems Engineering Publications by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. Computer Simulation of an Unsprung Vehicle, Part I Abstract The mechanics of unsprung wheel tractors has received extensive study in the last 40 years. The quantitative approach to the problem essentially began with the work of McKibben (7) in the 1920s. Twenty years later, Worthington (12) analyzed the effect of pneumatic tires on tractor stabiIity. Later, Buchele (3) drew on land- locomotion theory to introduce soil variables into the equations for tractor stability. Differential equations were avoided in these analyses by assuming that the tractor moved with zero or constant acceleration. Thus, vibration and actual tipping of the tractor were beyond the scope of the analyses. Disciplines Agriculture | Bioresource and Agricultural Engineering Comments This article is published as Goering, C. -

Computing Simplicial Homology Based on Efficient Smith Normal Form Algorithms
Computing Simplicial Homology Based on Efficient Smith Normal Form Algorithms Jean-Guillaume Dumas1, Frank Heckenbach2, David Saunders3, and Volkmar Welker4 1 Laboratoire de Mod´elisation et Calcul, IMAG-B. P. 53, 38041 Grenoble, France 2 Universit¨atErlangen-N¨urnberg, Mathematisches Institut, Bismarckstr. 1 1/2, 91054 Erlangen, Germany 3 University of Delaware, Department of Computer and Information Sciences, Newark, DE 19716, USA 4 Philipps-Universit¨atMarburg, Fachbereich Mathematik und Informatik, 35032 Marburg, Germany Abstract. We recall that the calculation of homology with integer coefficients of a simplicial complex reduces to the calculation of the Smith Normal Form of the boundary matrices which in general are sparse. We provide a review of several al- gorithms for the calculation of Smith Normal Form of sparse matrices and compare their running times for actual boundary matrices. Then we describe alternative ap- proaches to the calculation of simplicial homology. The last section then describes motivating examples and actual experiments with the GAP package that was im- plemented by the authors. These examples also include as an example of other homology theories some calculations of Lie algebra homology. 1 Introduction Geometric properties of topological spaces are often conveniently expressed by algebraic invariants of the space. Notably the fundamental group, the higher homotopy groups, the homology groups and the cohomology algebra play a prominent role in this respect. This paper focuses on methods for the computer calculation of the homology of finite simplicial complexes and its applications (see comments on the other invariants in Section 7). We assume that the topological space, whose homology we want to cal- culate, is given as an abstract simplicial complex. -

Reed-Solomon Encoding and Decoding
Bachelor's Thesis Degree Programme in Information Technology 2011 León van de Pavert REED-SOLOMON ENCODING AND DECODING A Visual Representation i Bachelor's Thesis | Abstract Turku University of Applied Sciences Degree Programme in Information Technology Spring 2011 | 37 pages Instructor: Hazem Al-Bermanei León van de Pavert REED-SOLOMON ENCODING AND DECODING The capacity of a binary channel is increased by adding extra bits to this data. This improves the quality of digital data. The process of adding redundant bits is known as channel encod- ing. In many situations, errors are not distributed at random but occur in bursts. For example, scratches, dust or fingerprints on a compact disc (CD) introduce errors on neighbouring data bits. Cross-interleaved Reed-Solomon codes (CIRC) are particularly well-suited for detection and correction of burst errors and erasures. Interleaving redistributes the data over many blocks of code. The double encoding has the first code declaring erasures. The second code corrects them. The purpose of this thesis is to present Reed-Solomon error correction codes in relation to burst errors. In particular, this thesis visualises the mechanism of cross-interleaving and its ability to allow for detection and correction of burst errors. KEYWORDS: Coding theory, Reed-Solomon code, burst errors, cross-interleaving, compact disc ii ACKNOWLEDGEMENTS It is a pleasure to thank those who supported me making this thesis possible. I am thankful to my supervisor, Hazem Al-Bermanei, whose intricate know- ledge of coding theory inspired me, and whose lectures, encouragement, and support enabled me to develop an understanding of this subject. -

The Binary Golay Code and the Leech Lattice
The binary Golay code and the Leech lattice Recall from previous talks: Def 1: (linear code) A code C over a field F is called linear if the code contains any linear combinations of its codewords A k-dimensional linear code of length n with minimal Hamming distance d is said to be an [n, k, d]-code. Why are linear codes interesting? ● Error-correcting codes have a wide range of applications in telecommunication. ● A field where transmissions are particularly important is space probes, due to a combination of a harsh environment and cost restrictions. ● Linear codes were used for space-probes because they allowed for just-in-time encoding, as memory was error-prone and heavy. Space-probe example The Hamming weight enumerator Def 2: (weight of a codeword) The weight w(u) of a codeword u is the number of its nonzero coordinates. Def 3: (Hamming weight enumerator) The Hamming weight enumerator of C is the polynomial: n n−i i W C (X ,Y )=∑ Ai X Y i=0 where Ai is the number of codeword of weight i. Example (Example 2.1, [8]) For the binary Hamming code of length 7 the weight enumerator is given by: 7 4 3 3 4 7 W H (X ,Y )= X +7 X Y +7 X Y +Y Dual and doubly even codes Def 4: (dual code) For a code C we define the dual code C˚ to be the linear code of codewords orthogonal to all of C. Def 5: (doubly even code) A binary code C is called doubly even if the weights of all its codewords are divisible by 4. -

Nonlinear Control of Underactuated Mechanical Systems with Application to Robotics and Aerospace Vehicles
Nonlinear Control of Underactuated Mechanical Systems with Application to Robotics and Aerospace Vehicles by Reza Olfati-Saber Submitted to the Department of Electrical Engineering and Computer Science in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Electrical Engineering and Computer Science at the MASSACHUSETTS INSTITUTE OF TECHNOLOGY February 2001 © Massachusetts Institute of Technology 2001. All rights reserved. Author ................................................... Department of Electrical Engineering and Computer Science January 15, 2000 C ertified by.......................................................... Alexandre Megretski, Associate Professor of Electrical Engineering Thesis Supervisor Accepted by............................................ Arthur C. Smith Chairman, Department Committee on Graduate Students Nonlinear Control of Underactuated Mechanical Systems with Application to Robotics and Aerospace Vehicles by Reza Olfati-Saber Submitted to the Department of Electrical Engineering and Computer Science on January 15, 2000, in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Electrical Engineering and Computer Science Abstract This thesis is devoted to nonlinear control, reduction, and classification of underac- tuated mechanical systems. Underactuated systems are mechanical control systems with fewer controls than the number of configuration variables. Control of underactu- ated systems is currently an active field of research due to their broad applications in Robotics, Aerospace Vehicles, and Marine Vehicles. The examples of underactuated systems include flexible-link robots, nobile robots, walking robots, robots on mo- bile platforms, cars, locomotive systems, snake-type and swimming robots, acrobatic robots, aircraft, spacecraft, helicopters, satellites, surface vessels, and underwater ve- hicles. Based on recent surveys, control of general underactuated systems is a major open problem. Almost all real-life mechanical systems possess kinetic symmetry properties, i.e. -

Erste Arbeiten Mit Zuse-Computern
HERMANN FLESSNER ERSTE ARBEITEN MIT ZUSE-COMPUTERN BAND 1 Erste Arbeiten mit Zuse-Computern Mit einem Geleitwort von Prof. Dr.-Ing. Horst Zuse Band 1 Rechnen, Planen und Konstruieren mit Computern Von Prof. em. Dr.-Ing. Hermann Flessner Universit¨at Hamburg Mit 166 Abbildungen Prof. em. Dr.-Ing. Hermann Flessner Geboren 1930 in Hamburg. Nach Abitur 1950 – 1952 Zimmererlehre in Dusseldorf.¨ 1953 – 1957 Studium des Bauingenieurwesens an der Technischen Hochschule Hannover. 1958 – 1962 Statiker undKonstrukteurinderEd.Zublin¨ AG. 1962 Wiss. Mitarbeiter am Institut fur¨ Massivbau der TH Hannover; dort 1964 Lehrauftrag und 1965 Promotion. Ebd. 1966 Professor fur¨ Elektronisches Rechnen im Bauwesen. 1968 – 1978 Professor fur¨ Angewandte Informatik im Ingenieurwesen an der Ruhr-Universit¨at Bochum; 1969 – 70 zwischenzeitlich Gastprofessor am Massachusetts Institute of Technology (M.I.T.), Cambridge, USA. Ab 1978 Ordentl. Professor fur¨ Angewandte Informatik in Naturwissenschaft und Technik an der Universit¨at Hamburg. Dort 1994 Emeritierung, danach beratender Ingenieur. Biografische Information der Deutschen Nationalbibliothek Die Deutsche Nationalbibliothek verzeichnet diese Publikation in der Deutschen Nationalbibliothek; detaillierte bibliografische Daten sind im Internet uber¨ http://dnb.d-nb.de abrufbar uber:¨ Flessner, Hermann: Erste Arbeiten mit ZUSE-Computern, Band 1 Dieses Werk ist urheberrechtlich geschutzt.¨ Die dadurch begrundeten¨ Rechte, insbesondere die der Ubersetzung,¨ des Nachdrucks, der Entnahme von Abbildungen, der Wiedergabe auf photomechani- schem oder digitalem Wege und der Speicherung in Datenverarbeitungsanlagen bzw. Datentr¨agern jeglicher Art bleiben, auch bei nur auszugsweiser Verwertung, vorbehalten. c 2016 H. Flessner, D - 21029 Hamburg 2. Auflage 2017 Herstellung..und Verlag:nBoD – Books on Demand, Norderstedt Text und Umschlaggestaltung: Hermann Flessner ISBN: 978-3-7412-2897-1 V Geleitwort Hermann Flessner kenne ich, pr¨aziser gesagt, er kennt mich als 17-j¨ahrigen seit ca.