DOCSLIB.ORG

Finding Cyclic Redundancy Check Polynomials for Multilevel Systems James A

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Finding Cyclic Redundancy Check Polynomials for Multilevel Systems James A View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by University of Richmond University of Richmond UR Scholarship Repository Math and Computer Science Faculty Publications Math and Computer Science 10-1998 Finding Cyclic Redundancy Check Polynomials for Multilevel Systems James A. Davis University of Richmond, [email protected] Miranda Mowbray Simon Crouch Follow this and additional works at: http://scholarship.richmond.edu/mathcs-faculty-publications Part of the Mathematics Commons Recommended Citation Davis, James A., Miranda Mowbray, and Simon Crouch. "Finding Cyclic Redundancy Check Polynomials for Multilevel Systems." IEEE Transactions on Communications 46, no. 10 (October 1998): 1250-253. This Article is brought to you for free and open access by the Math and Computer Science at UR Scholarship Repository. It has been accepted for inclusion in Math and Computer Science Faculty Publications by an authorized administrator of UR Scholarship Repository. For more information, please contact [email protected]. 1250 IEEE TRANSACTIONS ON COMMUNICATIONS, VOL. 46, NO. 10, OCTOBER 1998 Finding Cyclic Redundancy Check Polynomials for ,Multilevel Systems James A. Davis, Miranda Mowbray, and Simon Crouch Abstract-This letter describes a technique for finding cyclic for using all nine levels rather than, effectively, just eight, redundancy check polynomials for systems for transmission over in that with nine levels there are more possible choices for symmetric channels which encode information in multiple voltage code words which do not encode data, but are special signals levels, so that the resulting redundancy check gives good error protection and is efficient to implement. The codes which we used for synchronization information or to signal the end of construct have a Hamming distance of 3 or 4. We discuss a way the packet. The greater choice for nondata codewords allows to reduce burst error in parallel transmissions and some tricks run lengths to be kept short and allows for more efficient for efficient implementation of the shift register for these poly­ clock recovery. The other alternative mentioned, working over nomials. We illustrate our techniques by discussing a particular GF(9), does not have any advantages over Z in terms of example where the number of levels is 9, but they are applicable 9 in general. complexity of algebraic operations, and it seems harder to explain. Thus, we will construct codes over Z9 in this letter. Index Terms-Communication systems, cyclic codes, multilevel We assume that the reader is familiar with CRC's over systems, polynomials. GF(2): see [1] for background. In Section II, we describe how to choose a CRC over GF(3) with Hamming distance 4-i.e., I. INTRODUCTION so that error resulting in a change in up to three symbols in the N AN EFFORT to have high-speed transmission without packet will be detected. In Section III, we show how to use I exceeding emissions regulations, engineers have turned to this to construct CRC' s over Z 9 with Hamming distance 4. In transmissions which encode information in multiple voltage Section IV, we briefly discuss two implementation issues. levels in place of the traditional binary transmission with two voltage levels. In order to ensure reliable transmission, some error detection needs to be included. This letter de~cribes how II. POLYNOMIAL OF GF(3) to choose a cyclic redundancy check polynomial (CRC) in We will ultimately want to have error protection for a nine­ such a system, and we also discuss how to implement such level system. In order to do that, we first need to construe! a system, describing a technique which increases protection a system which will work for a three-level system. We will against burst errors, and efficient implementation of the shift extend this in Section IV, but we state without proof at thh register. We will assume that the transmission channel is the stage that the nine-level system will have error detectior. multilevel symmetric channel, so that if the voltage level capabilities at least as good as the three-level system used received is in error, each of the possible wrong levels is equally to generate it. We start with a well-known lemma. (The proofr likely to occur. For this channel, the most suitable distance of all the lemmas are in the Appendix.) measure is the Hamming distance. Lemma 1: Suppose that P(x) is a primitive polynomial We will focus our attention on a system with nine levels over GF(3) with degree d > 1, and that n is an integer less because of the particular application out of which this arose, than (3d - 1)/2. Then the code generated by P truncated at but everything that we discuss can be done in a more general length n has a Hamming distance of at least 3. setting. We chose to work with cyclic codes over Z 9 because In order to increase the Hamming distance of the code these codes are relatively easy to work with both theoretically we are using to 4 (which would detect any error altering as well as practically, but there are other choices. We could at most three symbols in the packet), we can modify a have constructed a cyclic code over GF(9), the finite field with standard technique from binary transmissions: when working nine elements, or we could have constructed a cyclic code over with cyclie codes over GF(2), any code whose generator is either Z8 or GF(8) (finite ring or field with eight elements) divisible by ( x+ 1) will detect any error altering an odd number and then had one signal level which is never used. The latter of symbols in the packet. Thus, we can take a cyclic code over suggestion came from a referee and was not considered during GF(2) whose Hamming distance is 3 and construct a new code the original work done on the code. Such a code would be no whose Hamming distance is 4 by multiplying the generator by less efficient than our nine-level coding; but there is a reason (x + 1). This technique does not directly work over GF(3), but the following lemma demonstrates that we can perform a Paper approved by S. B. Wicker, the Editor for Coding Theory and similar trick. Techniques of the IEEE Communications Society. Manuscript received March Lemma 2: Suppose that g(x) is a generator of a truncated 1. 1997; revised February 16, 1998. J. A. Davis was with Hewlett-Packard Laboratories, Bristol, BS34 6QZ cyclic code over GF(3) of length n and Hamming distance at U.K., on sabbatical from the Department of Mathematics and Computer least·3. Then the code of length n generated by (x - l)g(x) Science, University of Richmond, Richmond, VA 23173 USA. has Hamming distance of at least 4 if and only if there are no M. Mowbray and S. Crouch are with Hewlett-Packard Laboratories, Bristol · ""k · 0m-k k · BS34 6QZ U.K. codewords of the form L..i=l xm-i - L..j=l xm- -i, m <; n Publisher Item Identifier S 0090-6778(98)07771-X. in the truncated code generated by g(x). 0090-6778/98$10.00 © 1998 IEEE IEEE TRANSACTIONS ON COMMUNICATIONS, VOL. 46, NO. 10, OCTOBER 1998 1251 We will show later that if b(x) is the generator for a will construct by multiplying together three elements truncated cyclic code over GF(3) = Z3 with Hamming whose orders are 2, 1871, and 34511, respectively. distance h, then the truncated cyclic code over Z9 whose So we need to find an element of order 34 511. If 2 2 1871 generator is b(x) [considered as a polynomial over Z9 rather (x + 1) < ) is not 1 in the field, then it will be than GF(3)] will also have Hamming distance h .. In our an element of order 34 511. (If it is equal to 1, take application, we work with packets which have a maximum another .irreducible polynomial in place of x2 + 1 length of 4500 bytes (the size of Token Ring packets). Each and try again.) To do this, first use Mathematica byte is to be encoded as a triple of nine-level symbols. (This to compute the powers of x with the command coding is not as efficient as sending the bytes directly, but Do[g[x_, i_J := PolynomialPowerMod[x, i, £17 + x{4 allows for special code words which do not encode data, as +£13 + x"9 + x7 + x'5 + x'3+x - 1, 3], i, 1, 5000] then explained in the introduction.) Thus, the detection scheme rewrite (x2 + 1)2<1871 ) as ((x2 + 1)729 )5 ((x2 + 1) 81 ) will be a truncated nine-level cyclic code of length at most ( (x2+1 )9).( (x2+1) 7) =( (x1458 + l)s(x162+ l)(x18+1) 13 500. Since the length of the packets that we will be sending (x2 + 1) 7), exploiting the fact that raising polynomials is at most 13 500, if we find a primitive polynomial over to powers of 3 is easy mod 3; this can be GF(3) of degree at least 10, then by the first Lemma this computed using the Mathematica command will generate a truncated code with Hamming distance 3. PolynomialMod[PolynomialRemainder[ ( (g[x, 1458] Multiplying this primitive polynomial by (x - 1) will give +1)'5) * (g[x, 162] :+- 1) * (g[x, 18] + 1) * ((x'2 + 1)7), a polynomial of degree at least 11, which by the second £17 +x"14 + £13 + x'9 + x7 + x'5 + x'°3 + x - 1], 3] Lemma will generate a truncated code with Hamming distance which yields the result 1 +x2 +x4 +x5 +x11 +x13 -xl4 4 as long as we avoid codewords of the specified form.
Load more

Recommended publications
  • 16-Channel DAS with 16-Bit, Bipolar Input, Dual Simultaneous Sampling
    16-Channel DAS with 16-Bit, Bipolar Input, Dual Simultaneous Sampling ADC Data Sheet AD7616 FEATURES APPLICATIONS 16-channel, dual, simultaneously sampled inputs Power line monitoring Independently selectable channel input ranges Protective relays True bipolar: ±10 V, ±5 V, ±2.5 V Multiphase motor control Single 5 V analog supply and 2.3 V to 3.6 V VDRIVE supply Instrumentation and control systems Fully integrated data acquisition solution Data acquisition systems (DASs) Analog input clamp protection GENERAL DESCRIPTION Input buffer with 1 MΩ analog input impedance First-order antialiasing analog filter The AD7616 is a 16-bit, DAS that supports dual simultaneous On-chip accurate reference and reference buffer sampling of 16 channels. The AD7616 operates from a single 5 V Dual 16-bit successive approximation register (SAR) ADC supply and can accommodate ±10 V, ±5 V, and ±2.5 V true bipolar Throughput rate: 2 × 1 MSPS input signals while sampling at throughput rates up to 1 MSPS Oversampling capability with digital filter per channel pair with 90.5 dB SNR. Higher SNR performance can Flexible sequencer with burst mode be achieved with the on-chip oversampling mode (92 dB for an Flexible parallel/serial interface oversampling ratio (OSR) of 2). SPI/QSPI/MICROWIRE/DSP compatible The input clamp protection circuitry can tolerate voltages up to Optional cyclic redundancy check (CRC) error checking ±21 V. T h e AD7616 has 1 MΩ analog input impedance, regardless Hardware/software configuration of sampling frequency. The single-supply operation, on-chip Performance filtering, and high input impedance eliminate the need for 92 dB SNR at 500 kSPS (2× oversampling) driver op amps and external bipolar supplies.
    [Show full text]
  • The CLASP Application Security Process
    The CLASP Application Security Process Secure Software, Inc. Copyright (c) 2005, Secure Software, Inc. The CLASP Application Security Process The CLASP Application Security Process TABLE OF CONTENTS CHAPTER 1 Introduction 1 CLASP Status 4 An Activity-Centric Approach 4 The CLASP Implementation Guide 5 The Root-Cause Database 6 Supporting Material 7 CHAPTER 2 Implementation Guide 9 The CLASP Activities 11 Institute security awareness program 11 Monitor security metrics 12 Specify operational environment 13 Identify global security policy 14 Identify resources and trust boundaries 15 Identify user roles and resource capabilities 16 Document security-relevant requirements 17 Detail misuse cases 18 Identify attack surface 19 Apply security principles to design 20 Research and assess security posture of technology solutions 21 Annotate class designs with security properties 22 Specify database security configuration 23 Perform security analysis of system requirements and design (threat modeling) 24 Integrate security analysis into source management process 25 Implement interface contracts 26 Implement and elaborate resource policies and security technologies 27 Address reported security issues 28 Perform source-level security review 29 Identify, implement and perform security tests 30 The CLASP Application Security Process i Verify security attributes of resources 31 Perform code signing 32 Build operational security guide 33 Manage security issue disclosure process 34 Developing a Process Engineering Plan 35 Business objectives 35 Process
    [Show full text]
  • IS 13737 (1993): Isoinformation Technology
    इंटरनेट मानक Disclosure to Promote the Right To Information Whereas the Parliament of India has set out to provide a practical regime of right to information for citizens to secure access to information under the control of public authorities, in order to promote transparency and accountability in the working of every public authority, and whereas the attached publication of the Bureau of Indian Standards is of particular interest to the public, particularly disadvantaged communities and those engaged in the pursuit of education and knowledge, the attached public safety standard is made available to promote the timely dissemination of this information in an accurate manner to the public. “जान का अधकार, जी का अधकार” “परा को छोड न 5 तरफ” Mazdoor Kisan Shakti Sangathan Jawaharlal Nehru “The Right to Information, The Right to Live” “Step Out From the Old to the New” IS 13737 (1993): ISOInformation Technology - 130 mm Rewritable optical disk cartridges for information interchange [LITD 16: Computer Hardware, Peripherals and Identification Cards] “ान $ एक न भारत का नमण” Satyanarayan Gangaram Pitroda “Invent a New India Using Knowledge” “ान एक ऐसा खजाना > जो कभी चराया नह जा सकताह ै”ै Bhartṛhari—Nītiśatakam “Knowledge is such a treasure which cannot be stolen” IS 13737 : 1993 ISO/IEC 10089 : 1991 CONTENTS Page NationalForeword..........,..........................................‘.““““’ . (vii) 1 Scope 1 2 Conformance 1 3 Normative references 1 4 Conventions and notations 1 5 List of acronyms 2 6 Definitions 2 2 6. I case 2 6.2 Clamping Zone 6.3
    [Show full text]
  • 1. Background This Paper Is About a Method for Recovering Data from Floppy Disks That Are Failing Due to “Weak Bits”
    A Method for Recovering Data From Failing Floppy Disks with a Practical Example Dr. Frederick B. Cohen, Ph.D. and Charles M. Preston Fred Cohen & Associates and California Sciences Institute Abstract: As floppy disks and other similar media age, they have a tendency to lose data because of the reduction in retention of electromagnetic fields over time associated with various environmental degradation factors. In attempting to read these disks, the coding techniques used to write them can be exploited along with the proposed fault mechanisms to demonstrate that repetitions of read attempts under proper conditions yield valid data subject to specific error modes. In many cases those errors can be partially or completely reversed by analysis of read results. A practical example involving a case of substantial legal value is used as an example of the application of these methods. Keywords: weak bits, floppy disks, digital forensics, coding, field density loss, the birthday problem, error inversion 1. Background This paper is about a method for recovering data from floppy disks that are failing due to “weak bits”. It describes a repetitive read technique that has successfully recovered data from failing floppy disks in forensic cases and describes analysis of the results of such repetitive reads in terms of yielding forensically sound data values. These techniques are not new or particularly unique; however, they are not widely published and analysis necessary to support their use in legal matters has not been found elsewhere. The particular matter used as an example in this analysis involved a floppy disk that was more than 15 years old and that contained the only copy of a binary assembled version of a software program that was subject to intellectual property claims of sufficient value to warrant recovery beyond the means normally used by commercial recovery firms.
    [Show full text]
  • Floppy Disc Controller Instruction Manual
    Part Number 2120-0067 OQ419 FLOPPY DISC CONTROLLER INSTRUCTION MANUAL March 1985 DISTRIBUTED LOGIC CORPORATION 1555 S. Sinclair Street P.O. Box 6270 ~R Anaheim, California 92806 I nmmI Telephone: (714) 937·5700 Telex: 6836051 Contents SECTION 1 - GENERAL INFORMATION 1.1 INTRODUCTION 1 1.2 GENERAL DESCRIPTION 2 1.3 COMPATIBILITY 2 1.4 LOGICAL TRACK FORMAT 3 1.4.1 Sector Header Field 3 1.4.2 Data Field 5 1.4.3 CRC - Cyclic Redundancy Check 5 1.5 RECORDING SCHEME 6 1.6 SPECIFICATIONS 6 SECTION 2 - INSTALLATION 2.1 CONTROLLER JUMPER CONFIGURATIONS 7 2.1.1 Device and Vector Address Selection 8 2.1.2 Device Interrupt Priority 9 2.1.3 Bootstrap 10 2.1.4 Wri te Precompensati on 10 2.1.5 Write Current Control 11 2.1.6 Drive Step Rate 11 2.2 DRIVE CONFIGURATIONS 11 2.3 CABLING 19 2.4 CONTROLLER INSTALLATION 21 2.5 INITIAL CHECKOUT 21 SECTION 3 - OPERATION 3.1 GENERAL INFORHATION 23 3.2 BOOTSTRAPPING 23 3.3 FORMATTING 24 3.4 FILL/WRITE OPERATION 25 3.5 READ/EMPTY OPERATION 27 3.6 OPERATION USING RT-ll 27 SECTION 4 - PROGRAMMING 4.1 GENERAL INFORMATION 29 4.2 COMMAND AND STATUS REGISTER - RXVCS (177170) 30 4.3 DATA BUFFER (177172) 31 4.3.1 Data Buffer Register (RXVDB) 32 4.3.2 Trace Address Register (RXVTA) 32 4.3.3 Sector Address Register (RXVSA) 32 4.3.4 Word Count Register (RXVWC) 32 4.3.5 Bus Address Register (RXVBA) 33 4.3.6 Error and Status Register (RXVES) 33 4.3.7 Bus Address Extension Register (RXVBAE) 35 i i ; 4.4 EXTENDED STATUS REGISTERS 35 4.5 COMMAND PROTOCOL 36 4.5.1 Fill Buffer (000) 36 4.5.2 Empty Buffer (001) 37 4.5.3 Write Buffer
    [Show full text]
  • High Performance Table-Based Algorithm for Pipelined CRC Calculation
    High Performance Table-Based Algorithm for Pipelined CRC Calculation Yan Sun and Min Sik Kim School of Electrical Engineering and Computer Science Washington State University Pullman, Washington 99164-2752, U.S.A. Email: fysun,[email protected] Abstract—In this paper, we present a fast cyclic redun- for message length detection of variable-length message dancy check (CRC) algorithm that performs CRC compu- communications [4], [5]. tation for an arbitrary length of message in parallel. For a Communication networks use protocols with ever in- given message with any length, the algorithm first chunks the message into blocks, each of which has a fixed size equal creasing demands on speed. The increasing performance to the degree of the generator polynomial. Then it computes needs can be fulfilled by using ASICs (Application Spe- CRC for the chunked blocks in parallel using lookup tables, cific Integrated Circuits) and this will probably also be and the results are combined together with XOR operations. the case in the future. Meeting the speed requirement In the traditional implementation, it is the feedback that is crucial because packets will be dropped if processing makes pipelining problematic. In the proposed algorithm, we solve this problem by taking advantage of CRC’s properties is not completed at wire speed. Recently, protocols for and pipelining the feedback loop. The short pipeline latency high throughput have emerged, such as IEEE 802.11n of our algorithm enables a faster clock frequency than WLAN and UWB (Ultra Wide Band), and new protocols previous approaches, and it also allows easy scaling of the with even higher throughput requirement are on the way.
    [Show full text]
  • A Method for Recovering Data from Failing Floppy Disk Drives
    A Method for Recovering Data From Failing Floppy Disk Drives Dr. Frederick B. Cohen, Ph.D. and Charles Preston Background: This paper is about a method for recovering data from floppy disks that are failing due to weak bits. It describes a repetitive read technique that has successfully recovered data from failing floppies in forensic cases and describes other related techniques. None of these techniques are new or particularly unique, however, they are not widely published to the best of the authors knowledge and some of the related analysis may be helpful in making more definitive determinations in some cases. The nature of 'weak' bits and failure modes: Floppy disks tend to degrade in various ways over time and under various environmental conditions such as temperature, humidity, and so forth. In some cases this results in the presence of so-called “weak” bits on the media. Weak bits are bits that are sufficiently degraded in their electromagnetic field so as to yield voltages between the values for a '1' and a '0' when read by the read heads on most floppy disks. This is a result of reduced flux density in the electromagnetic media. In particular, the floppy disk coding used in most current disks is identified in: http://cma.zdnet.com/book/upgraderepair/ch14/ch14.htm as Modified Frequency Modulation (MFM) which uses timed flux density transitions to indicate bits. In particular, it uses a “No transition, Transition” (NT) sequence to indicate a “1”, a TN to indicate a '0' preceded by a '0', and an NN to indicate a '0' preceded by a '1'.
    [Show full text]
  • Introduction to Coding Theory
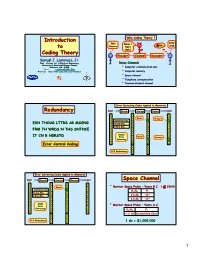
    Introduction Why Coding Theory ? Introduction Info Info Noise ! Info »?# Sink to Source Heh ! Sink Heh ! Coding Theory Encoder Channel Decoder Samuel J. Lomonaco, Jr. Dept. of Comp. Sci. & Electrical Engineering Noisy Channels University of Maryland Baltimore County Baltimore, MD 21250 • Computer communication line Email: [email protected] WebPage: http://www.csee.umbc.edu/~lomonaco • Computer memory • Space channel • Telephone communication • Teacher/student channel Error Detecting Codes Applied to Memories Redundancy Input Encode Storage Detect Output 1 1 1 1 0 0 0 0 1 1 Error 1 Erasure 1 1 31=16+5 Code 1 0 ? 0 0 0 0 EVN THOUG LTTRS AR MSSNG 1 16 Info Bits 1 1 1 0 5 Red. Bits 0 0 0 0 0 0 0 FRM TH WRDS N THS SNTNCE 1 1 1 1 0 0 0 0 1 1 1 Double 1 IT CN B NDRSTD 0 0 0 0 1 Error 1 Error 1 Erasure 1 1 Detecting 1 0 ? 0 0 0 0 1 1 1 1 Error Control Coding 0 0 1 1 0 0 31% Redundancy 1 1 1 1 Error Correcting Codes Applied to Memories Input Encode Storage Correct Output Space Channel 1 1 1 1 0 0 0 0 Mariner Space Probe – Years B.C. ( ≤ 1964) 1 1 Error 1 1 • 1 31=16+5 Code 1 0 1 0 0 0 0 Eb/N0 Pe 16 Info Bits 1 1 1 1 -3 0 5 Red. Bits 0 0 0 6.8 db 10 0 0 0 0 -5 1 1 1 1 9.8 db 10 0 0 0 0 1 1 1 Single 1 0 0 0 0 Error 1 1 • Mariner Space Probe – Years A.C.
    [Show full text]
  • Acronyms Appendix
    APPENDIX A Acronyms Table A-1 defines the acronyms that are used in this publication. Ta b l e A- 1 L i s t o f Ac ro ny m s Acronym Expansion AAL ATM adaptation layer ACE access control entry ACL access control list ACNS Application and Content Networking System AFI authority and format identifier Agport aggregation port ALPS Airline Protocol Support AMP Active Monitor Present APaRT Automated Packet Recognition and Translation ARP Address Resolution Protocol ATA Analog Telephone Adaptor ATM Asynchronous Transfer Mode AV attribute value BDD binary decision diagrams BECN backward explicit congestion notification BGP Border Gateway Protocol Bidir bidirectional PIM BPDU bridge protocol data unit BRF bridge relay function BSC Bisync BSTUN Block Serial Tunnel BUS broadcast and unknown server BVI bridge-group virtual interface CAM content-addressable memory CAR committed access rate Catalyst 6500 Series Switch Content Switching Module with SSL Command Reference OL-6237-01 A-1 Appendix A Acronyms Table A-1 List of Acronyms (continued) Acronym Expansion CBAC context based access control CCA circuit card assembly CDP Cisco Discovery Protocol CEF Cisco Express Forwarding CHAP Challenge Handshake Authentication Protocol CIR committed information rate CIST Common and Internal Spanning Tree CLI command-line interface CLNS Connection-Less Network Service CMNS Connection-Mode Network Service CNS Cisco Networking Services COPS Common Open Policy Server COPS-DS Common Open Policy Server Differentiated Services CoS class of service CPLD Complex Programmable
    [Show full text]
  • Reed-Solomon Encoding and Decoding
    Bachelor's Thesis Degree Programme in Information Technology 2011 León van de Pavert REED-SOLOMON ENCODING AND DECODING A Visual Representation i Bachelor's Thesis | Abstract Turku University of Applied Sciences Degree Programme in Information Technology Spring 2011 | 37 pages Instructor: Hazem Al-Bermanei León van de Pavert REED-SOLOMON ENCODING AND DECODING The capacity of a binary channel is increased by adding extra bits to this data. This improves the quality of digital data. The process of adding redundant bits is known as channel encod- ing. In many situations, errors are not distributed at random but occur in bursts. For example, scratches, dust or fingerprints on a compact disc (CD) introduce errors on neighbouring data bits. Cross-interleaved Reed-Solomon codes (CIRC) are particularly well-suited for detection and correction of burst errors and erasures. Interleaving redistributes the data over many blocks of code. The double encoding has the first code declaring erasures. The second code corrects them. The purpose of this thesis is to present Reed-Solomon error correction codes in relation to burst errors. In particular, this thesis visualises the mechanism of cross-interleaving and its ability to allow for detection and correction of burst errors. KEYWORDS: Coding theory, Reed-Solomon code, burst errors, cross-interleaving, compact disc ii ACKNOWLEDGEMENTS It is a pleasure to thank those who supported me making this thesis possible. I am thankful to my supervisor, Hazem Al-Bermanei, whose intricate know- ledge of coding theory inspired me, and whose lectures, encouragement, and support enabled me to develop an understanding of this subject.
    [Show full text]
  • The Binary Golay Code and the Leech Lattice
    The binary Golay code and the Leech lattice Recall from previous talks: Def 1: (linear code) A code C over a field F is called linear if the code contains any linear combinations of its codewords A k-dimensional linear code of length n with minimal Hamming distance d is said to be an [n, k, d]-code. Why are linear codes interesting? ● Error-correcting codes have a wide range of applications in telecommunication. ● A field where transmissions are particularly important is space probes, due to a combination of a harsh environment and cost restrictions. ● Linear codes were used for space-probes because they allowed for just-in-time encoding, as memory was error-prone and heavy. Space-probe example The Hamming weight enumerator Def 2: (weight of a codeword) The weight w(u) of a codeword u is the number of its nonzero coordinates. Def 3: (Hamming weight enumerator) The Hamming weight enumerator of C is the polynomial: n n−i i W C (X ,Y )=∑ Ai X Y i=0 where Ai is the number of codeword of weight i. Example (Example 2.1, [8]) For the binary Hamming code of length 7 the weight enumerator is given by: 7 4 3 3 4 7 W H (X ,Y )= X +7 X Y +7 X Y +Y Dual and doubly even codes Def 4: (dual code) For a code C we define the dual code C˚ to be the linear code of codewords orthogonal to all of C. Def 5: (doubly even code) A binary code C is called doubly even if the weights of all its codewords are divisible by 4.
    [Show full text]
  • Programming Embedded Systems, Second Edition with C and GNU Development Tools
    Programming Embedded Systems Second Edition Programming Embedded Systems, Second Edition with C and GNU Development Tools Foreword If you mention the word embedded to most people, they'll assume you're talking about reporters in a war zone. Few dictionaries—including the canonical Oxford English Dictionary—link embedded to computer systems. Yet embedded systems underlie nearly all of the electronic devices used today, from cell phones to garage door openers to medical instruments. By now, it's nearly impossible to build anything electronic without adding at least a small microprocessor and associated software. Vendors produce some nine billion microprocessors every year. Perhaps 100 or 150 million of those go into PCs. That's only about one percent of the units shipped. The other 99 percent go into embedded systems; clearly, this stealth business represents the very fabric of our highly technological society. And use of these technologies will only increase. Solutions to looming environmental problems will surely rest on the smarter use of resources enabled by embedded systems. One only has to look at the network of 32-bit processors in Toyota's hybrid Prius to get a glimpse of the future. Page 1 Programming Embedded Systems Second Edition Though prognostications are difficult, it is absolutely clear that consumers will continue to demand ever- brainier products requiring more microprocessors and huge increases in the corresponding software. Estimates suggest that the firmware content of most products doubles every 10 to 24 months. While the demand for more code is increasing, our productivity rates creep up only slowly. So it's also clear that the industry will need more embedded systems people in order to meet the demand.
    [Show full text]