Micromechanics of Dislocations in Solids: $ J $-, $ M $-, and $ L
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

10-1 CHAPTER 10 DEFORMATION 10.1 Stress-Strain Diagrams And
EN380 Naval Materials Science and Engineering Course Notes, U.S. Naval Academy CHAPTER 10 DEFORMATION 10.1 Stress-Strain Diagrams and Material Behavior 10.2 Material Characteristics 10.3 Elastic-Plastic Response of Metals 10.4 True stress and strain measures 10.5 Yielding of a Ductile Metal under a General Stress State - Mises Yield Condition. 10.6 Maximum shear stress condition 10.7 Creep Consider the bar in figure 1 subjected to a simple tension loading F. Figure 1: Bar in Tension Engineering Stress () is the quotient of load (F) and area (A). The units of stress are normally pounds per square inch (psi). = F A where: is the stress (psi) F is the force that is loading the object (lb) A is the cross sectional area of the object (in2) When stress is applied to a material, the material will deform. Elongation is defined as the difference between loaded and unloaded length ∆푙 = L - Lo where: ∆푙 is the elongation (ft) L is the loaded length of the cable (ft) Lo is the unloaded (original) length of the cable (ft) 10-1 EN380 Naval Materials Science and Engineering Course Notes, U.S. Naval Academy Strain is the concept used to compare the elongation of a material to its original, undeformed length. Strain () is the quotient of elongation (e) and original length (L0). Engineering Strain has no units but is often given the units of in/in or ft/ft. ∆푙 휀 = 퐿 where: is the strain in the cable (ft/ft) ∆푙 is the elongation (ft) Lo is the unloaded (original) length of the cable (ft) Example Find the strain in a 75 foot cable experiencing an elongation of one inch. -
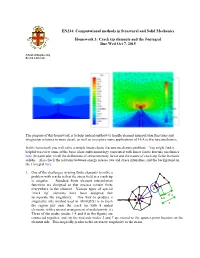
Crack Tip Elements and the J Integral
EN234: Computational methods in Structural and Solid Mechanics Homework 3: Crack tip elements and the J-integral Due Wed Oct 7, 2015 School of Engineering Brown University The purpose of this homework is to help understand how to handle element interpolation functions and integration schemes in more detail, as well as to explore some applications of FEA to fracture mechanics. In this homework you will solve a simple linear elastic fracture mechanics problem. You might find it helpful to review some of the basic ideas and terminology associated with linear elastic fracture mechanics here (in particular, recall the definitions of stress intensity factor and the nature of crack-tip fields in elastic solids). Also check the relations between energy release rate and stress intensities, and the background on the J integral here. 1. One of the challenges in using finite elements to solve a problem with cracks is that the stress field at a crack tip is singular. Standard finite element interpolation functions are designed so that stresses remain finite a everywhere in the element. Various types of special b c ‘crack tip’ elements have been designed that 3L/4 incorporate the singularity. One way to produce a L/4 singularity (the method used in ABAQUS) is to mesh L the region just near the crack tip with 8 noded elements, with a special arrangement of nodal points: (i) Three of the nodes (nodes 1,4 and 8 in the figure) are connected together, and (ii) the mid-side nodes 2 and 7 are moved to the quarter-point location on the element side. -

Cross-Linked Polymers and Rubber Elasticity Chapter 9 (Sperling)
Cross-linked Polymers and Rubber Elasticity Chapter 9 (Sperling) • Definition of Rubber Elasticity and Requirements • Cross-links, Networks, Classes of Elastomers (sections 1-3, 16) • Simple Theory of Rubber Elasticity (sections 4-8) – Entropic Origin of Elastic Retractive Forces – The Ideal Rubber Behavior • Departures from the Ideal Rubber Behavior (sections 9-11) – Non-zero Energy Contribution to the Elastic Retractive Forces – Stress-induced Crystallization and Limited Extensibility of Chains (How to make better elastomers: High Strength and High Modulus) – Network Defects (dangling chains, loops, trapped entanglements, etc..) – Semi-empirical Mooney-Rivlin Treatment (Affine vs Non-Affine Deformation) Definition of Rubber Elasticity and Requirements • Definition of Rubber Elasticity: Very large deformability with complete recoverability. • Molecular Requirements: – Material must consist of polymer chains. Need to change conformation and extension under stress. – Polymer chains must be highly flexible. Need to access conformational changes (not w/ glassy, crystalline, stiff mat.) – Polymer chains must be joined in a network structure. Need to avoid irreversible chain slippage (permanent strain). One out of 100 monomers must connect two different chains. Connections (covalent bond, crystallite, glassy domain in block copolymer) Cross-links, Networks and Classes of Elastomers • Chemical Cross-linking Process: Sol-Gel or Percolation Transition • Gel Characteristics: – Infinite Viscosity – Non-zero Modulus – One giant Molecule – Solid -

Chapter 10: Elasticity and Oscillations
Chapter 10 Lecture Outline 1 Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Chapter 10: Elasticity and Oscillations •Elastic Deformations •Hooke’s Law •Stress and Strain •Shear Deformations •Volume Deformations •Simple Harmonic Motion •The Pendulum •Damped Oscillations, Forced Oscillations, and Resonance 2 §10.1 Elastic Deformation of Solids A deformation is the change in size or shape of an object. An elastic object is one that returns to its original size and shape after contact forces have been removed. If the forces acting on the object are too large, the object can be permanently distorted. 3 §10.2 Hooke’s Law F F Apply a force to both ends of a long wire. These forces will stretch the wire from length L to L+L. 4 Define: L The fractional strain L change in length F Force per unit cross- stress A sectional area 5 Hooke’s Law (Fx) can be written in terms of stress and strain (stress strain). F L Y A L YA The spring constant k is now k L Y is called Young’s modulus and is a measure of an object’s stiffness. Hooke’s Law holds for an object to a point called the proportional limit. 6 Example (text problem 10.1): A steel beam is placed vertically in the basement of a building to keep the floor above from sagging. The load on the beam is 5.8104 N and the length of the beam is 2.5 m, and the cross-sectional area of the beam is 7.5103 m2. -
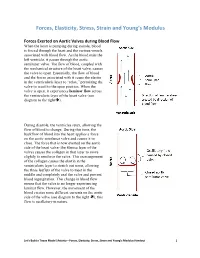
Forces, Elasticity, Stress, Strain and Young's Modulus Handout
Forces, Elasticity, Stress, Strain and Young’s Modulus Forces Exerted on Aortic Valves during Blood Flow When the heart is pumping during systole, blood is forced through the heart and the various vessels associated with blood flow. As the blood exits the left ventricle, it passes through the aortic semilunar valve. The flow of blood, coupled with the mechanical structure of the heart valve, causes the valve to open. Essentially, the flow of blood and the forces associated with it cause the elastin in the ventricularis layer to “relax,” permitting the valve to recoil to the open position. When the valve is open, it experiences laminar flow across the ventricularis layer of the heart valve (see diagram to the right). During diastole, the ventricles relax, allowing the flow of blood to change. During this time, the backflow of blood into the heart applies a force on the aortic semilunar valve and causes it to close. The force that is now exerted on the aortic side of the heart valve (the fibrosa layer of the valve) causes the collagen in that layer to move slightly to reinforce the valve. This rearrangement of the collagen causes the elastin in the ventricularis layer to stretch out some, allowing the three leaflets of the valve to meet in the middle and completely seal the valve and prevent blood regurgitation. This change in blood flow means that the valve is no longer experiencing laminar flow. However, the movement of the blood creates some different currents on the aortic side of the valve (see diagram to the right ); this flow is oscillatory in nature. -

Elasticity of Materials at High Pressure by Arianna Elizabeth Gleason A
Elasticity of Materials at High Pressure By Arianna Elizabeth Gleason A dissertation submitted in partial satisfaction of the Requirements for the degree of Doctor of Philosophy in Earth and Planetary Science in the GRADUATE DIVISION of the UNIVERSITY OF CALIFORNIA, BERKELEY Committee in charge: Professor Raymond Jeanloz, Chair Professor Hans-Rudolf Wenk Professor Kenneth Raymond Fall 2010 Elasticity of Materials at High Pressure Copyright 2010 by Arianna Elizabeth Gleason 1 Abstract Elasticity of Materials at High Pressure by Arianna Elizabeth Gleason Doctor of Philosophy in Earth and Planetary Science University of California, Berkeley Professor Raymond Jeanloz, Chair The high-pressure behavior of the elastic properties of materials is important for condensed matter and materials physics, and planetary and geosciences, as it contributes to the mechanical deformations and stability of solids under external stresses. The high-pressure elasticity of relevant minerals is of substantial geophysical importance for the Earth’s interior since they relate to (1) velocities of seismic waves and (2) the change in density that occurs when minerals are under pressure. Absence of samples from the deep interior prompts comparisons between seismological observations and the elastic properties of candidate minerals as a way to extract information regarding the composition and mineralogy of the Earth. Implementing a new method for measuring compressional- and shear-wave velocities, Vp and Vs, based on Brillouin spectroscopy of polycrystalline materials at high pressures, I examine four case studies: 1) soda-lime glass, 2) NaCl, 3) MgO, and 4) Kilauea basalt glass. The results on multigrain soda-lime glass show that even with an index differing by 3 percent, an oil medium removes the effects of multiple scattering from the Brillouin spectra of the glass powders; similarly, high-pressure Brillouin spectra from transparent polycrystalline samples should, in many cases, be free from optical-scattering effects. -

Basics Elements on Linear Elastic Fracture Mechanics and Crack Growth Modeling Sylvie Pommier
Basics elements on linear elastic fracture mechanics and crack growth modeling Sylvie Pommier To cite this version: Sylvie Pommier. Basics elements on linear elastic fracture mechanics and crack growth modeling. Doctoral. France. 2017. cel-01636731 HAL Id: cel-01636731 https://hal.archives-ouvertes.fr/cel-01636731 Submitted on 16 Nov 2017 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Basics elements on linear elastic fracture mechanics and crack growth modeling Sylvie Pommier, LMT (ENS Paris-Saclay, CNRS, Université Paris-Saclay) Fail Safe Damage Tolerant Design • Consider the eventuality of damage or of the presence of defects, • predict if these defects or damage may lead to fracture, • and, in the event of failure, predicts the consequences (size, velocity and trajectory of the fragments) 2 Foundations of fracture mechanics : The Liberty Ships • 2700 Liberty Ships were built between 1942 and the end of WWII • The production rate was of 70 ships / day • duration of construction: 5 days • 30% of ships built in 1941 have suffered catastrophic failures • 362 lost ships The fracture mechanics concepts were still unknown Causes of fracture: hiver 1941 hiver • Welded Structure rather than bolted, – offering a substantial assembly time gain but with a continuous path offered for ships cracks to propagate through the structure. -

Module 3 Constitutive Equations
Module 3 Constitutive Equations Learning Objectives • Understand basic stress-strain response of engineering materials. • Quantify the linear elastic stress-strain response in terms of tensorial quantities and in particular the fourth-order elasticity or stiffness tensor describing Hooke's Law. • Understand the relation between internal material symmetries and macroscopic anisotropy, as well as the implications on the structure of the stiffness tensor. • Quantify the response of anisotropic materials to loadings aligned as well as rotated with respect to the material principal axes with emphasis on orthotropic and transversely- isotropic materials. • Understand the nature of temperature effects as a source of thermal expansion strains. • Quantify the linear elastic stress and strain tensors from experimental strain-gauge measurements. • Quantify the linear elastic stress and strain tensors resulting from special material loading conditions. 3.1 Linear elasticity and Hooke's Law Readings: Reddy 3.4.1 3.4.2 BC 2.6 Consider the stress strain curve σ = f() of a linear elastic material subjected to uni-axial stress loading conditions (Figure 3.1). 45 46 MODULE 3. CONSTITUTIVE EQUATIONS σ ˆ 1 2 ψ = 2 Eǫ E 1 ǫ Figure 3.1: Stress-strain curve for a linear elastic material subject to uni-axial stress σ (Note that this is not uni-axial strain due to Poisson effect) In this expression, E is Young's modulus. Strain Energy Density For a given value of the strain , the strain energy density (per unit volume) = ^(), is defined as the area under the curve. In this case, 1 () = E2 2 We note, that according to this definition, @ ^ σ = = E @ In general, for (possibly non-linear) elastic materials: @ ^ σij = σij() = (3.1) @ij Generalized Hooke's Law Defines the most general linear relation among all the components of the stress and strain tensor σij = Cijklkl (3.2) In this expression: Cijkl are the components of the fourth-order stiffness tensor of material properties or Elastic moduli. -

Contact Mechanics
International Journal of Solids and Structures 37 (2000) 29±43 www.elsevier.com/locate/ijsolstr Contact mechanics J.R. Barber a,*, M. Ciavarella b, 1 aDepartment of Mechanical Engineering and Applied Mechanics, University of Michigan, Ann Arbor, MI 48109-2125, USA bDepartment of Engineering Science, University of Oxford, Parks Road, Oxford, OX1 3PJ, UK Abstract Contact problems are central to Solid Mechanics, because contact is the principal method of applying loads to a deformable body and the resulting stress concentration is often the most critical point in the body. Contact is characterized by unilateral inequalities, describing the physical impossibility of tensile contact tractions (except under special circumstances) and of material interpenetration. Additional inequalities and/or non-linearities are introduced when friction laws are taken into account. These complex boundary conditions can lead to problems with existence and uniqueness of quasi-static solution and to lack of convergence of numerical algorithms. In frictional problems, there can also be lack of stability, leading to stick±slip motion and frictional vibrations. If the material is non-linear, the solution of contact problems is greatly complicated, but recent work has shown that indentation of a power-law material by a power law punch is self-similar, even in the presence of friction, so that the complete history of loading in such cases can be described by the (usually numerical) solution of a single problem. Real contacting surfaces are rough, leading to the concentration of contact in a cluster of microscopic actual contact areas. This aects the conduction of heat and electricity across the interface as well as the mechanical contact process. -

Chapter 9B -- Conservation of Momentum
ChapterChapter 9B9B -- ConservationConservation ofof MomentumMomentum AAA PowerPointPowerPointPowerPoint PresentationPresentationPresentation bybyby PaulPaulPaul E.E.E. Tippens,Tippens,Tippens, EmeritusEmeritusEmeritus ProfessorProfessorProfessor SouthernSouthernSouthern PolytechnicPolytechnicPolytechnic StateStateState UniversityUniversityUniversity © 2007 Momentum is conserved in this rocket launch. The velocity of the rocket and its payload is determined by the mass and velocity of the expelled gases. Photo: NASA NASA Objectives:Objectives: AfterAfter completingcompleting thisthis module,module, youyou shouldshould bebe ableable to:to: •• StateState thethe lawlaw ofof conservationconservation ofof momentummomentum andand applyapply itit toto thethe solutionsolution ofof problems.problems. •• DistinguishDistinguish byby definitiondefinition andand exampleexample betweenbetween elasticelastic andand inelasticinelastic collisions.collisions. •• PredictPredict thethe velocitiesvelocities ofof twotwo collidingcolliding bodiesbodies whenwhen givengiven thethe coefficientscoefficients ofof restitution,restitution, masses,masses, andand initialinitial velocities.velocities. AA CollisionCollision ofof TwoTwo MassesMasses When two masses m1 and m2 collide, we will use the symbol u to describe velocities before collision. BeforeBefore u1 u2 m1 m2 The symbol v will describe velocities after collision. v AfterAfter v 1 m 2 m1 2 AA CollisionCollision ofof TwoTwo BlocksBlocks BeforeBefore u1 u2 m1 m2 Collision “u”= Before “v” = After m1 m2B AfterAfter -

Chapter 11 – Equilibrium and Elasticity
Chapter 11 – Equilibrium and Elasticity I. Equilibrium - Definition - Requirements - Static equilibrium II. Center of gravity III. Elasticity - Tension and compression - Shearing - Hydraulic stress I. Equilibrium - Definition: An object is in equilibrium if: - The linear momentum of its center of mass is constant. - Its angular momentum about its center of mass is constant. Example: block resting on a table, hockey puck sliding across a frictionless surface with constant velocity, the rotating blades of a ceiling fan, the wheel of a bike traveling across a straight path at constant speed. - Static equilibrium: P = ,0 L = 0 Objects that are not moving either in TRANSLATION or ROTATION Example: block resting on a table . Stable static equilibrium: If a body returns to a state of static equilibrium after having been displaced from it by a force marble at the bottom of a spherical bowl. Unstable static equilibrium: A small force can displace the body and end the equilibrium. (1)Torque about supporting edge by Fg is 0 because line of action of Fg passes through rotation axis domino in equilibrium. (2) Slight force ends equilibrium line of action of Fg moves to one side of supporting edge torque due to Fg increases domino rotation. (3) Not as unstable as (1) in order to topple it, one needs to rotate it beyond balance position in (1). - Requirements of equilibrium: dP P = cte → F = = 0 Balance of forces translational equilibrium net dt dL L = cte , τ = = 0 Balance of torques rotational equilibrium net dt - Vector sum of all external forces that act on body must be zero. -

Chapter 18. Elasticity and Solid-State Geophysics
Chapter 18 Elasticity and solid-state geophysics Mark well the various kinds of constants. TI1ese are usually the bulk modulus K minerals, note their properties and and the rigidity G or fL Young's modulus E and Poisson's ratio cr are also commonly used. TI1ere their mode of origin. are, correspondingly, two types of elastic waves; Petrus Severinus (I 57 I) the compressional, or primary (P), and the shear, or secondary (S) , having velocities derivable from The seismic properties of a material depend on pVi = K +4G/3 = K +4J.L/3 composition, crystal structure, temperature, pres pVl = G = fL sure and in some cases defect and impurity con centrations. Most of the Earth is made up of The interrelations between the elastic constants crystals. The elastic properties of crystals depend and wave velocities are given in Table 18.1. In an on orientation and frequency. TI1us, the inter anisotropic solid there are two shear waves and pretation of seismic data, or the extrapolation one compressional wave in any given direction. of laboratory data, requires knowledge of crystal Only gases, fluids, well-annealed glasses and or mineral physics, elasticity and thermodynam similar noncrystalline materials are strictly ics. But one cannot directly infer composition isotropic. Crystalline material with random ori or temperature from mantle tomography and a entations of grains can approach isotropy, but table of elastic constants derived from laboratory rocks are generally anisotropic. experiments. Seismic velocities are not unique Laboratory measurements of mineral elas functions of temperature and pressure alone nor tic properties, and their temperature and pres are they linear functions of them.