DOCSLIB.ORG

Experimental and Numerical Study of Orthotropic Materials

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Experimental and Numerical Study of Orthotropic Materials Master's Degree Thesis ISRN: BTH-AMT-EX--2017/D18--SE Experimental and Numerical Study of Orthotropic Materials Ram Kiran Kesana Yashpal Surendhar Goud Pulicherla Department of Mechanical Engineering Blekinge Institute of Technology Karlskrona, Sweden 2017 Supervisors: Sharon Kao-Walter, Shafiqul Islam, Madeleine Hermann, BTH Experimental and Numerical Study of Orthotropic Materials Ram Kiran Kesana Yashpal Surendhar Goud Pulicherla Department of Mechanical Engineering. Blekinge Institute of Technology. Karlskrona, Sweden. 2017. Thesis submitted for completion of Master of Science in Mechanical Engineering with emphasis on Structural Mechanics at the Department of Mechanical Engineering, Blekinge Institute of Technology, Karlskrona, Sweden. Abstract: In current enterprises, simulations are being utilized to reduce the cost of product development. Along this line, there is an increased enthusiasm for enhancing reliability and accuracy of the simulations. For an accurate and reliable simulation, it is essential to use an accurate material model and provide it with accurate material information. In current scenario, orthotropic materials are being simulated utilizing isotropic material model, as orthotropic material model requires more material data which is not promptly accessible. This research intends to test and identify orthotropic materials and simulate them using orthotropic material model in ABAQUS. Materials utilized as a part of this research were Aluminium, LDPE, PET. Required material data was derived by performing Uni- directional tensile tests, DIC, and an algorithm developed. To get highly accurate material data from DIC, a few kinds of patterns were examined, and a superior pattern was resolved for camera configuration being utilized. Keywords: Digital image correlation(DIC), Inverses method, Low-density polyethylene (LDPE), Polyethylene Terephthalate (PET), Optimization. Acknowledgements This master thesis has been completed at the Department of Mechanical Engineering at Blekinge Institute of Technology (BTH), Karlskrona, Sweden in participation with Tetra Pak AB, Lund, Sweden. We would like to thank our supervisor at BTH, Sharon Kao-Walter for her direction, help and support amid our work. We might likewise express gratitude towards Tetra Pak for providing material utilized as a part of experimental work. We wish to express our genuine gratefulness to Shafiqul Islam and Madeleine Hermann for assisting us with their thoughts, recommendations and perceptions. We are thankful to Wureguli Reheman for suggestions in composing the report for our thesis. We are obliged to the Mechanical Department of BTH for providing the access to the lab equipment, machinery and accessories required for our experiments and CAD lab for simulations to complete our task. Karlskrona, October 2017. 2 Contents List of Tables 5 List of Figures 6 Notations 8 Introduction 10 Materials 10 Background 10 Objective and Method of work 12 Research Questions 14 Theoretical Groundwork 15 Fundamentals of Solid Mechanics 15 Hooke’s Law 16 Yield Surface 17 Lankford Coefficient 17 Hill Yield Criterion 18 Elastic-Plastic 20 Material Model 21 Isotropic Behaviour 21 Orthotropic Behaviour 21 Orthotropic Elasticity 21 Orthotropic Plasticity 23 Inverse Method 24 Digital Image Correlation (DIC) 24 Literature Review 26 Experimental Work 29 Experimental Setup 29 Equipment Configuration 31 Specimen Preparation 32 Experimental Procedure 35 MATLAB 36 Numerical Simulation 41 Components of simulation 42 Elastic Model 42 Plastic Model 42 Element types 43 3 Optimization Procedure 44 Overview 44 Implementation 45 Code Structure 47 DIC working procedure using GOM Correlate 50 Pattern Review 51 Extraction of data 55 Results 56 GOM Correlate 56 Yield Stress Ratios 58 Orthotropic Models 59 Discussions and Conclusions 66 Discussion on Tensile tests 67 Contribution to research 67 Future Work 68 References 70 APPENDIX 71 Plots of data from Experiments 71 True stress-strain plots 77 Load cell calculations 80 Data from recorded videos of LDPE specimen 80 Procedure 81 Modelling in ABAQUS 81 GOM Correlate 84 Modified INP file 86 Considering only one guess variable 88 Programming Scripts 88 MATLAB 88 Python 90 Related images 91 4 List of Tables Table 5.1. Youngs Modulus of materials from MATLAB using Experimental data. 40 Table 9.1. Width change ratio of materials from GOM Correlate. 56 Table 9.2. Width change at 20% elongation during the test from GOM Correlate. 57 Table 9.3. Young's Modulus of materials from GOM Correlate. 58 Table 9.4. Yield stress ratios from Inverse method. 58 Table 12.1. Yield stress data considering only one guess. 88 5 List of Figures Figure 2.1. Force vs Displacement curve parts. .................................................... 13 Figure 5.1. Tensile-testing Machine. ..................................................................... 30 Figure 5.2. Grippers for Aluminium. .................................................................... 30 Figure 5.3. Pneumatic Grippers for LDPE and PET. ............................................ 31 Figure 5.4. Machine and Cross direction. ............................................................. 32 Figure 5.5. (a) Specimen cutting directions. (b) Specimen dimensions. .......... 34 Figure 5.6. Force vs Displacement of LDPE from the experiment. ...................... 37 Figure 5.7. Force vs Displacement of PET from the experiment. ......................... 38 Figure 5.8. Load vs Displacement of 4mm Aluminium from the experiment. ..... 38 Figure 5.9. Load vs Displacement of 2mm Aluminium from the experiment. ..... 39 Figure 7.1.Core tasks. ............................................................................................ 45 Figure 7.2. Code working flowchart. .................................................................... 48 Figure 8.1. DIC spray patterns on Aluminium specimens. ................................... 50 Figure 8.2. Pattern review. .................................................................................... 51 Figure 8.3. Three Surface Components. ................................................................ 52 Figure 8.4. (a) Less diverse grey scale. (b) Dark spot. (c) White spot near dark area. ....................................................................................................................... 52 Figure 8.5. Suitable pattern for DIC. ..................................................................... 54 Figure 8.6. Results from suitable pattern. ............................................................. 55 Figure 9.1. Orthotropic Aluminium 2mm MD. ..................................................... 60 Figure 9.2. Orthotropic Aluminium 2mm CD. ...................................................... 60 Figure 9.3. Orthotropic Aluminium 2mm 45degrees. ........................................... 61 Figure 9.4. Orthotropic PET MD. ......................................................................... 62 Figure 9.5. Orthotropic PET CD. .......................................................................... 62 Figure 9.6. Orthotropic PET 45 degrees. ............................................................... 63 Figure 9.7. Orthotropic LDPE MD. ...................................................................... 64 Figure 9.8. Orthotropic LDPE CD. ....................................................................... 64 Figure 9.9. Orthotropic LDPE 45degrees. ............................................................. 65 Figure 10.1. Comparison of old pattern with new MATLAB pattern. .................. 68 Figure 12.1. Load vs Displacements of PET MD for all specimens. .................... 71 Figure 12.2. Load vs Displacements of PET CD for all specimens. ..................... 72 Figure 12.3. Load vs displacements of PET 45 degree of all specimens. ............. 72 Figure 12.4. Load vs displacements of LDPE MD for all specimens. .................. 73 Figure 12.5. Load vs displacements of LDPE CD for all specimens. ................... 73 Figure 12.6. Load vs displacements of LDPE 45 degree for all specimens. ......... 74 Figure 12.7. Load vs displacements of Aluminium 4mm MD for all specimens. 74 Figure 12.8. Load vs displacements of Aluminium 4mm CD for all specimens. 75 6 Figure 12.9. Load vs displacements of Aluminium 4mm 45 degree for all specimens. ............................................................................................................. 75 Figure 12.10. Load vs displacements of Aluminium 2mm MD for all specimens. 76 Figure 12.11. Load vs displacements of Aluminium 2mm CD for all specimens. 76 Figure 12.12. Load vs displacements of Aluminium 2mm 45 degree for all specimens. ............................................................................................................. 77 Figure 12.13. True stress-strain curves of PET. .................................................... 78 Figure 12.14. True stress-strain curves of LDPE. ................................................. 78 Figure 12.15. True stress-strain curves of Aluminium 4mm. ................................ 79 Figure 12.16. True stress-strain curves of Aluminium 2mm. ................................ 79 Figure 12.17. (a) 45degrees. (b) CD. (c) MD. .................. 81 Figure 12.18. Material data. ................................................................................... 82 Figure 12.19. 45-degree model with material orientation. .................................... 83 Figure 12.20. Increments. .....................................................................................
Load more

Recommended publications
  • 10-1 CHAPTER 10 DEFORMATION 10.1 Stress-Strain Diagrams And
    EN380 Naval Materials Science and Engineering Course Notes, U.S. Naval Academy CHAPTER 10 DEFORMATION 10.1 Stress-Strain Diagrams and Material Behavior 10.2 Material Characteristics 10.3 Elastic-Plastic Response of Metals 10.4 True stress and strain measures 10.5 Yielding of a Ductile Metal under a General Stress State - Mises Yield Condition. 10.6 Maximum shear stress condition 10.7 Creep Consider the bar in figure 1 subjected to a simple tension loading F. Figure 1: Bar in Tension Engineering Stress () is the quotient of load (F) and area (A). The units of stress are normally pounds per square inch (psi). = F A where: is the stress (psi) F is the force that is loading the object (lb) A is the cross sectional area of the object (in2) When stress is applied to a material, the material will deform. Elongation is defined as the difference between loaded and unloaded length ∆푙 = L - Lo where: ∆푙 is the elongation (ft) L is the loaded length of the cable (ft) Lo is the unloaded (original) length of the cable (ft) 10-1 EN380 Naval Materials Science and Engineering Course Notes, U.S. Naval Academy Strain is the concept used to compare the elongation of a material to its original, undeformed length. Strain () is the quotient of elongation (e) and original length (L0). Engineering Strain has no units but is often given the units of in/in or ft/ft. ∆푙 휀 = 퐿 where: is the strain in the cable (ft/ft) ∆푙 is the elongation (ft) Lo is the unloaded (original) length of the cable (ft) Example Find the strain in a 75 foot cable experiencing an elongation of one inch.
    [Show full text]
  • Static Analysis of Isotropic, Orthotropic and Functionally Graded Material Beams
    Journal of Multidisciplinary Engineering Science and Technology (JMEST) ISSN: 2458-9403 Vol. 3 Issue 5, May - 2016 Static analysis of isotropic, orthotropic and functionally graded material beams Waleed M. Soliman M. Adnan Elshafei M. A. Kamel Dep. of Aeronautical Engineering Dep. of Aeronautical Engineering Dep. of Aeronautical Engineering Military Technical College Military Technical College Military Technical College Cairo, Egypt Cairo, Egypt Cairo, Egypt [email protected] [email protected] [email protected] Abstract—This paper presents static analysis of degrees of freedom for each lamina, and it can be isotropic, orthotropic and Functionally Graded used for long and short beams, this laminated finite Materials (FGMs) beams using a Finite Element element model gives good results for both stresses and deflections when compared with other solutions. Method (FEM). Ansys Workbench15 has been used to build up several models to simulate In 1993 Lidstrom [2] have used the total potential different types of beams with different boundary energy formulation to analyze equilibrium for a conditions, all beams have been subjected to both moderate deflection 3-D beam element, the condensed two-node element reduced the size of the of uniformly distributed and transversal point problem, compared with the three-node element, but loads within the experience of Timoshenko Beam increased the computing time. The condensed two- Theory and First order Shear Deformation Theory. node system was less numerically stable than the The material properties are assumed to be three-node system. Because of this fact, it was not temperature-independent, and are graded in the possible to evaluate the third and fourth-order thickness direction according to a simple power differentials of the strain energy function, and thus not law distribution of the volume fractions of the possible to determine the types of criticality constituents.
    [Show full text]
  • Constitutive Relations: Transverse Isotropy and Isotropy
    Objectives_template Module 3: 3D Constitutive Equations Lecture 11: Constitutive Relations: Transverse Isotropy and Isotropy The Lecture Contains: Transverse Isotropy Isotropic Bodies Homework References file:///D|/Web%20Course%20(Ganesh%20Rana)/Dr.%20Mohite/CompositeMaterials/lecture11/11_1.htm[8/18/2014 12:10:09 PM] Objectives_template Module 3: 3D Constitutive Equations Lecture 11: Constitutive relations: Transverse isotropy and isotropy Transverse Isotropy: Introduction: In this lecture, we are going to see some more simplifications of constitutive equation and develop the relation for isotropic materials. First we will see the development of transverse isotropy and then we will reduce from it to isotropy. First Approach: Invariance Approach This is obtained from an orthotropic material. Here, we develop the constitutive relation for a material with transverse isotropy in x2-x3 plane (this is used in lamina/laminae/laminate modeling). This is obtained with the following form of the change of axes. (3.30) Now, we have Figure 3.6: State of stress (a) in x1, x2, x3 system (b) with x1-x2 and x1-x3 planes of symmetry From this, the strains in transformed coordinate system are given as: file:///D|/Web%20Course%20(Ganesh%20Rana)/Dr.%20Mohite/CompositeMaterials/lecture11/11_2.htm[8/18/2014 12:10:09 PM] Objectives_template (3.31) Here, it is to be noted that the shear strains are the tensorial shear strain terms. For any angle α, (3.32) and therefore, W must reduce to the form (3.33) Then, for W to be invariant we must have Now, let us write the left hand side of the above equation using the matrix as given in Equation (3.26) and engineering shear strains.
    [Show full text]
  • Orthotropic Material Homogenization of Composite Materials Including Damping
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Lirias Orthotropic material homogenization of composite materials including damping A. Nateghia,e, A. Rezaeia,e,, E. Deckersa,d, S. Jonckheerea,b,d, C. Claeysa,d, B. Pluymersa,d, W. Van Paepegemc, W. Desmeta,d a KU Leuven, Department of Mechanical Engineering, Celestijnenlaan 300B box 2420, 3001 Heverlee, Belgium. E-mail: [email protected]. b Siemens Industry Software NV, Digital Factory, Product Lifecycle Management – Simulation and Test Solutions, Interleuvenlaan 68, B-3001 Leuven, Belgium. c Ghent University, Department of Materials Science & Engineering, Technologiepark-Zwijnaarde 903, 9052 Zwijnaarde, Belgium. d Member of Flanders Make. e SIM vzw, Technologiepark Zwijnaarde 935, B-9052 Ghent, Belgium. Introduction In the multiscale analysis of composite materials obtaining the effective equivalent material properties of the composite from the properties of its constituents is an important bridge between different scales. Although, a variety of homogenization methods are already in use, there is still a need for further development of novel approaches which can deal with complexities such as frequency dependency of material properties; which is specially of importance when dealing with damped structures. Time-domain methods Frequency-domain method Material homogenization is performed in two separate steps: Wave dispersion based homogenization is performed to a static step and a dynamic one. provide homogenized damping and material
    [Show full text]
  • Analysis of Deformation
    Chapter 7: Constitutive Equations Definition: In the previous chapters we’ve learned about the definition and meaning of the concepts of stress and strain. One is an objective measure of load and the other is an objective measure of deformation. In fluids, one talks about the rate-of-deformation as opposed to simply strain (i.e. deformation alone or by itself). We all know though that deformation is caused by loads (i.e. there must be a relationship between stress and strain). A relationship between stress and strain (or rate-of-deformation tensor) is simply called a “constitutive equation”. Below we will describe how such equations are formulated. Constitutive equations between stress and strain are normally written based on phenomenological (i.e. experimental) observations and some assumption(s) on the physical behavior or response of a material to loading. Such equations can and should always be tested against experimental observations. Although there is almost an infinite amount of different materials, leading one to conclude that there is an equivalently infinite amount of constitutive equations or relations that describe such materials behavior, it turns out that there are really three major equations that cover the behavior of a wide range of materials of applied interest. One equation describes stress and small strain in solids and called “Hooke’s law”. The other two equations describe the behavior of fluidic materials. Hookean Elastic Solid: We will start explaining these equations by considering Hooke’s law first. Hooke’s law simply states that the stress tensor is assumed to be linearly related to the strain tensor.
    [Show full text]
  • Crack Tip Elements and the J Integral
    EN234: Computational methods in Structural and Solid Mechanics Homework 3: Crack tip elements and the J-integral Due Wed Oct 7, 2015 School of Engineering Brown University The purpose of this homework is to help understand how to handle element interpolation functions and integration schemes in more detail, as well as to explore some applications of FEA to fracture mechanics. In this homework you will solve a simple linear elastic fracture mechanics problem. You might find it helpful to review some of the basic ideas and terminology associated with linear elastic fracture mechanics here (in particular, recall the definitions of stress intensity factor and the nature of crack-tip fields in elastic solids). Also check the relations between energy release rate and stress intensities, and the background on the J integral here. 1. One of the challenges in using finite elements to solve a problem with cracks is that the stress field at a crack tip is singular. Standard finite element interpolation functions are designed so that stresses remain finite a everywhere in the element. Various types of special b c ‘crack tip’ elements have been designed that 3L/4 incorporate the singularity. One way to produce a L/4 singularity (the method used in ABAQUS) is to mesh L the region just near the crack tip with 8 noded elements, with a special arrangement of nodal points: (i) Three of the nodes (nodes 1,4 and 8 in the figure) are connected together, and (ii) the mid-side nodes 2 and 7 are moved to the quarter-point location on the element side.
    [Show full text]
  • Cross-Linked Polymers and Rubber Elasticity Chapter 9 (Sperling)
    Cross-linked Polymers and Rubber Elasticity Chapter 9 (Sperling) • Definition of Rubber Elasticity and Requirements • Cross-links, Networks, Classes of Elastomers (sections 1-3, 16) • Simple Theory of Rubber Elasticity (sections 4-8) – Entropic Origin of Elastic Retractive Forces – The Ideal Rubber Behavior • Departures from the Ideal Rubber Behavior (sections 9-11) – Non-zero Energy Contribution to the Elastic Retractive Forces – Stress-induced Crystallization and Limited Extensibility of Chains (How to make better elastomers: High Strength and High Modulus) – Network Defects (dangling chains, loops, trapped entanglements, etc..) – Semi-empirical Mooney-Rivlin Treatment (Affine vs Non-Affine Deformation) Definition of Rubber Elasticity and Requirements • Definition of Rubber Elasticity: Very large deformability with complete recoverability. • Molecular Requirements: – Material must consist of polymer chains. Need to change conformation and extension under stress. – Polymer chains must be highly flexible. Need to access conformational changes (not w/ glassy, crystalline, stiff mat.) – Polymer chains must be joined in a network structure. Need to avoid irreversible chain slippage (permanent strain). One out of 100 monomers must connect two different chains. Connections (covalent bond, crystallite, glassy domain in block copolymer) Cross-links, Networks and Classes of Elastomers • Chemical Cross-linking Process: Sol-Gel or Percolation Transition • Gel Characteristics: – Infinite Viscosity – Non-zero Modulus – One giant Molecule – Solid
    [Show full text]
  • Chapter 10: Elasticity and Oscillations
    Chapter 10 Lecture Outline 1 Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Chapter 10: Elasticity and Oscillations •Elastic Deformations •Hooke’s Law •Stress and Strain •Shear Deformations •Volume Deformations •Simple Harmonic Motion •The Pendulum •Damped Oscillations, Forced Oscillations, and Resonance 2 §10.1 Elastic Deformation of Solids A deformation is the change in size or shape of an object. An elastic object is one that returns to its original size and shape after contact forces have been removed. If the forces acting on the object are too large, the object can be permanently distorted. 3 §10.2 Hooke’s Law F F Apply a force to both ends of a long wire. These forces will stretch the wire from length L to L+L. 4 Define: L The fractional strain L change in length F Force per unit cross- stress A sectional area 5 Hooke’s Law (Fx) can be written in terms of stress and strain (stress strain). F L Y A L YA The spring constant k is now k L Y is called Young’s modulus and is a measure of an object’s stiffness. Hooke’s Law holds for an object to a point called the proportional limit. 6 Example (text problem 10.1): A steel beam is placed vertically in the basement of a building to keep the floor above from sagging. The load on the beam is 5.8104 N and the length of the beam is 2.5 m, and the cross-sectional area of the beam is 7.5103 m2.
    [Show full text]
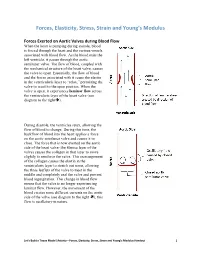
  • Forces, Elasticity, Stress, Strain and Young's Modulus Handout
    Forces, Elasticity, Stress, Strain and Young’s Modulus Forces Exerted on Aortic Valves during Blood Flow When the heart is pumping during systole, blood is forced through the heart and the various vessels associated with blood flow. As the blood exits the left ventricle, it passes through the aortic semilunar valve. The flow of blood, coupled with the mechanical structure of the heart valve, causes the valve to open. Essentially, the flow of blood and the forces associated with it cause the elastin in the ventricularis layer to “relax,” permitting the valve to recoil to the open position. When the valve is open, it experiences laminar flow across the ventricularis layer of the heart valve (see diagram to the right). During diastole, the ventricles relax, allowing the flow of blood to change. During this time, the backflow of blood into the heart applies a force on the aortic semilunar valve and causes it to close. The force that is now exerted on the aortic side of the heart valve (the fibrosa layer of the valve) causes the collagen in that layer to move slightly to reinforce the valve. This rearrangement of the collagen causes the elastin in the ventricularis layer to stretch out some, allowing the three leaflets of the valve to meet in the middle and completely seal the valve and prevent blood regurgitation. This change in blood flow means that the valve is no longer experiencing laminar flow. However, the movement of the blood creates some different currents on the aortic side of the valve (see diagram to the right ); this flow is oscillatory in nature.
    [Show full text]
  • Numerical Simulation of Excavations Within Jointed Rock of Infinite Extent
    NUMERICAL SIMULATION OF EXCAVATIONS WITHIN JOINTED ROCK OF INFINITE EXTENT by ALEXANDROS I . SOFIANOS (M.Sc.,D.I.C.) May 1984- - A thesis submitted for the degree of Doctor of Philosophy of the University of London Rock Mechanics Section, R.S.M.,Imperial College London SW7 2BP -2- A bstract The subject of the thesis is the development of a program to study i the behaviour of stratified and jointed rock masses around excavations. The rock mass is divided into two regions,one which is. supposed to * exhibit linear elastic behaviour,and the other which will include discontinuities that behave inelastically.The former has been simulated by a boundary integral plane strain orthotropic module,and the latter by quadratic joint,plane strain and membrane elements.The # two modules are coupled in one program.Sequences of loading include static point,pressure,body,and residual loads,construetion and excavation, and quasistatic earthquake load.The program is interactive with graphics. Problems of infinite or finite extent may be solved. Errors due to the coupling of the two numerical methods have been analysed. Through a survey of constitutive laws, idealizations of behaviour and test results for intact rock and discontinuities,appropriate models have been selected and parameter ♦ ranges identif i ed. The representation of the rock mass as an equivalent orthotropic elastic continuum has been investigated and programmed. Simplified theoretical solutions developed for the problem of a wedge on the roof of an opening have been compared with the computed results.A problem of open stoping is analysed. * ACKNOWLEDGEMENTS The author wishes to acknowledge the contribution of all members of the Rock Mechanics group at Imperial College to this work, and its full financial support by the State Scholarship Foundation of * G reece.
    [Show full text]
  • Composite Laminate Modeling
    Composite Laminate Modeling White Paper for Femap and NX Nastran Users Venkata Bheemreddy, Ph.D., Senior Staff Mechanical Engineer Adrian Jensen, PE, Senior Staff Mechanical Engineer Predictive Engineering Femap 11.1.2 White Paper 2014 WHAT THIS WHITE PAPER COVERS This note is intended for new engineers interested in modeling composites and experienced engineers who would like to get acquainted with the Femap interface. This note is intended to accompany a technical seminar and will provide you a starting background on composites. The following topics are covered: o A little background on the mechanics of composites and how micromechanics can be leveraged to obtain composite material properties o 2D composite laminate modeling Defining a material model, layup, property card and material angles Symmetric vs. unsymmetric laminate and why this is important Results post processing o 3D composite laminate modeling Defining a material model, layup, property card and ply/stack orientation When is a 3D model preferred over a 2D model o Modeling a sandwich composite Methods of modeling a sandwich composite 3D vs. 2D sandwich composite models and their pros and cons o Failure modeling of a 2D composite laminate Defining a laminate failure model Post processing laminate and lamina failure indices Predictive Engineering Document, Feel Free to Share With Your Colleagues Page 2 of 66 Predictive Engineering Femap 11.1.2 White Paper 2014 TABLE OF CONTENTS 1. INTRODUCTION ...........................................................................................................................................................
    [Show full text]
  • Dynamic Analysis of a Viscoelastic Orthotropic Cracked Body Using the Extended Finite Element Method
    Dynamic analysis of a viscoelastic orthotropic cracked body using the extended finite element method M. Toolabia, A. S. Fallah a,*, P. M. Baiz b, L.A. Louca a a Department of Civil and Environmental Engineering, Skempton Building, South Kensington Campus, Imperial College London SW7 2AZ b Department of Aeronautics, Roderic Hill Building, South Kensington Campus, Imperial College London SW7 2AZ Abstract The extended finite element method (XFEM) is found promising in approximating solutions to locally non-smooth features such as jumps, kinks, high gradients, inclusions, voids, shocks, boundary layers or cracks in solid or fluid mechanics problems. The XFEM uses the properties of the partition of unity finite element method (PUFEM) to represent the discontinuities without the corresponding finite element mesh requirements. In the present study numerical simulations of a dynamically loaded orthotropic viscoelastic cracked body are performed using XFEM and the J-integral and stress intensity factors (SIF’s) are calculated. This is achieved by fully (reproducing elements) or partially (blending elements) enriching the elements in the vicinity of the crack tip or body. The enrichment type is restricted to extrinsic mesh-based topological local enrichment in the current work. Thus two types of enrichment functions are adopted viz. the Heaviside step function replicating a jump across the crack and the asymptotic crack tip function particular to the element containing the crack tip or its immediately adjacent ones. A constitutive model for strain-rate dependent moduli and Poisson ratios (viscoelasticity) is formulated. A symmetric double cantilever beam (DCB) of a generic orthotropic material (mixed mode fracture) is studied using the developed XFEM code.
    [Show full text]