DOCSLIB.ORG

Chapter 10: Elasticity and Oscillations

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter 10: Elasticity and Oscillations Chapter 10 Lecture Outline 1 Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Chapter 10: Elasticity and Oscillations •Elastic Deformations •Hooke’s Law •Stress and Strain •Shear Deformations •Volume Deformations •Simple Harmonic Motion •The Pendulum •Damped Oscillations, Forced Oscillations, and Resonance 2 §10.1 Elastic Deformation of Solids A deformation is the change in size or shape of an object. An elastic object is one that returns to its original size and shape after contact forces have been removed. If the forces acting on the object are too large, the object can be permanently distorted. 3 §10.2 Hooke’s Law F F Apply a force to both ends of a long wire. These forces will stretch the wire from length L to L+L. 4 Define: L The fractional strain L change in length F Force per unit cross- stress A sectional area 5 Hooke’s Law (Fx) can be written in terms of stress and strain (stress strain). F L Y A L YA The spring constant k is now k L Y is called Young’s modulus and is a measure of an object’s stiffness. Hooke’s Law holds for an object to a point called the proportional limit. 6 Example (text problem 10.1): A steel beam is placed vertically in the basement of a building to keep the floor above from sagging. The load on the beam is 5.8104 N and the length of the beam is 2.5 m, and the cross-sectional area of the beam is 7.5103 m2. Find the vertical compression of the beam. Force of F L ceiling Y on beam A L F L L A Y Force of 9 floor on For steel Y = 20010 Pa. beam F L 5.8104 N 2.5 m L 1.0104 m A Y 7.5103 m2 200109 N/m2 7 Example (text problem 10.7): A 0.50 m long guitar string, of cross-sectional area 1.0106 m2, has a Young’s modulus of 2.0109 Pa. By how much must you stretch a guitar string to obtain a tension of 20 N? F L Y A L F L 20.0 N 0.5 m L A Y 1.0106 m2 2.0109 N/m2 5.0103 m 5.0 mm 8 §10.3 Beyond Hooke’s Law If the stress on an object exceeds the elastic limit, then the object will not return to its original length. An object will fracture if the stress exceeds the breaking point. The ratio of maximum load to the original cross- sectional area is called tensile strength. 9 The ultimate strength of a material is the maximum stress that it can withstand before breaking. 10 Example (text problem 10.10): An acrobat of mass 55 kg is going to hang by her teeth from a steel wire and she does not want the wire to stretch beyond its elastic limit. The elastic limit for the wire is 2.5108 Pa. What is the minimum diameter the wire should have to support her? F Want stress elastic limit A F mg A elastic limit elastic limit 2 D mg 2 elastic limit 4mg D 1.7103 m 1.7 mm elastic limit 11 §10.4 Shear and Volume Deformations A shear deformation occurs when two forces are applied on opposite surfaces of an object. 12 Shear Force F Shear Stress Surface Area A Define: displacement of surfaces x Shear Strain separation of surfaces L Hooke’s law (stressstrain) for shear deformations is F x S where S is the A L shear modulus 13 Example (text problem 10.25): The upper surface of a cube of gelatin, 5.0 cm on a side, is displaced by 0.64 cm by a tangential force. If the shear modulus of the gelatin is 940 Pa, what is the magnitude of the tangential force? F F From Hooke’s Law: x F x F SA S L A L 0.64 cm 940 N/m2 0.0025 m2 0.30 N 5.0 cm 14 An object completely submerged in a fluid will be squeezed on all sides. F volume stress pressure A V The result is a volume strain; volume strain V 15 For a volume deformation, Hooke’s Law is (stressstrain): V P B V where B is called the bulk modulus. The bulk modulus is a measure of how easy a material is to compress. 16 Example (text problem 10.24): An anchor, made of cast iron of bulk modulus 60.0109 Pa and a volume of 0.230 m3, is lowered over the side of a ship to the bottom of the harbor where the pressure is greater than sea level pressure by 1.75106 Pa. Find the change in the volume of the anchor. V P B V VP 0.230 m3 1.75106 Pa V B 60.0109 Pa 6.71106 m3 17 Deformations summary table Tensile or compressive Shear Volume Stress Force per unit Shear force divided Pressure cross-sectional by the area of the area surface on which it acts Strain Fractional Ratio of the relative Fractional change in displacement to the change in length separation of the two volume parallel surfaces Constant of Young’s Shear modulus (S) Bulk proportionality modulus (Y) Modulus (B) 18 §10.5 Simple Harmonic Motion Simple harmonic motion (SHM) occurs when the restoring force (the force directed toward a stable equilibrium point) is proportional to the displacement from equilibrium. 19 The motion of a mass on a spring is an example of SHM. Equilibrium position y x x The restoring force is F = kx. 20 Assuming the table is frictionless: F kx ma x x k a t xt x m 1 1 Also, Et KtUt mvt2 kxt2 2 2 21 At the equilibrium point x = 0 so a = 0 too. When the stretch is a maximum, a will be a maximum too. The velocity at the end points will be zero, and it is a maximum at the equilibrium point. 22 §10.6-7 Representing Simple Harmonic Motion When a mass-spring system is oriented vertically, it will exhibit SHM with the same period and frequency as a horizontally placed system. 23 SHM graphically 24 A simple harmonic oscillator can be described mathematically by: xt Acost x vt A sint t v at A 2 cost t where A is the amplitude of the motion, the maximum Or by: displacement from equilibrium, A = v , and A2 = a xt Asint max max. x vt A cost t v at A 2 sint t 25 2 The period of oscillation is T . where is the angular frequency of the k oscillations, k is the spring constant and m m is the mass of the block. 26 Example (text problem 10.30): The period of oscillation of an object in an ideal mass-spring system is 0.50 sec and the amplitude is 5.0 cm. What is the speed at the equilibrium point? At equilibrium x = 0: 1 1 1 E K U mv2 kx2 mv2 2 2 2 Since E = constant, at equilibrium (x = 0) the KE must be a maximum. Here v = vmax = A. 27 Example continued: The amplitude A is given, but is not. 2 2 12.6 rads/sec T 0.50 s and v Aω 5.0 cm12.6 rads/sec 62.8 cm/sec 28 Example (text problem 10.41): The diaphragm of a speaker has a mass of 50.0 g and responds to a signal of 2.0 kHz by moving back and forth with an amplitude of 1.8104 m at that frequency. (a) What is the maximum force acting on the diaphragm? 2 2 2 2 F Fmax mamax mA mA2f 4 mAf The value is Fmax=1400 N. 29 Example continued: (b) What is the mechanical energy of the diaphragm? Since mechanical energy is conserved, E = Kmax = Umax. 1 U kA2 The value of k is unknown so use K . max 2 max 1 2 Kmax mvmax 1 1 1 2 K mv2 mA2 mA2 2f 2 max 2 max 2 2 The value is Kmax= 0.13 J. 30 Example (text problem 10.47): The displacement of an object in SHM is given by: yt 8.00 cmsin1.57 rads/sec t What is the frequency of the oscillations? Comparing to y(t) = A sint gives A = 8.00 cm and = 1.57 rads/sec. The frequency is: 1.57 rads/sec f 0.250 Hz 2 2 31 Example continued: Other quantities can also be determined: 2 2 The period of the motion is T 4.00 sec 1.57 rads/sec xmax A 8.00 cm vmax A 8.00 cm1.57 rads/sec 12.6 cm/sec 2 2 2 amax A 8.00 cm1.57 rads/sec 19.7 cm/sec 32 §10.8 The Pendulum A simple pendulum is constructed by attaching a mass to a thin rod or a light string. We will also assume that the amplitude of the oscillations is small. 33 A simple pendulum: An FBD for the pendulum bob: L y T m x w 34 Fx mgsin mat Apply Newton’s 2nd Law to the pendulum bob. v2 F T mgcos m y r If we assume that <<1 rad, then sin and cos 1, the angular frequency of oscillations is then: g L 2 L The period of oscillations is T 2 g 35 Example (text problem 10.60): A clock has a pendulum that performs one full swing every 1.0 sec.
Load more

Recommended publications
  • 10-1 CHAPTER 10 DEFORMATION 10.1 Stress-Strain Diagrams And
    EN380 Naval Materials Science and Engineering Course Notes, U.S. Naval Academy CHAPTER 10 DEFORMATION 10.1 Stress-Strain Diagrams and Material Behavior 10.2 Material Characteristics 10.3 Elastic-Plastic Response of Metals 10.4 True stress and strain measures 10.5 Yielding of a Ductile Metal under a General Stress State - Mises Yield Condition. 10.6 Maximum shear stress condition 10.7 Creep Consider the bar in figure 1 subjected to a simple tension loading F. Figure 1: Bar in Tension Engineering Stress () is the quotient of load (F) and area (A). The units of stress are normally pounds per square inch (psi). = F A where: is the stress (psi) F is the force that is loading the object (lb) A is the cross sectional area of the object (in2) When stress is applied to a material, the material will deform. Elongation is defined as the difference between loaded and unloaded length ∆푙 = L - Lo where: ∆푙 is the elongation (ft) L is the loaded length of the cable (ft) Lo is the unloaded (original) length of the cable (ft) 10-1 EN380 Naval Materials Science and Engineering Course Notes, U.S. Naval Academy Strain is the concept used to compare the elongation of a material to its original, undeformed length. Strain () is the quotient of elongation (e) and original length (L0). Engineering Strain has no units but is often given the units of in/in or ft/ft. ∆푙 휀 = 퐿 where: is the strain in the cable (ft/ft) ∆푙 is the elongation (ft) Lo is the unloaded (original) length of the cable (ft) Example Find the strain in a 75 foot cable experiencing an elongation of one inch.
    [Show full text]
  • Phys 140A Lecture 8–Elastic Strain, Compliance, and Stiffness
    Lecture 8 Elastic strains, compliance, and stiffness Review for exam Stress: force applied to a unit area Strain: deformation resulting from stress Purpose of today’s derivations: Generalize Hooke’s law to a 3D body that may be subjected to any arbitrary force. We imagine 3 orthogonal vectors 풙̂, 풚̂, 풛̂ embedded in a solid before we have deformed it. After we have deformed the solid, these vectors might be of different length and they might be pointing in different directions. We describe these deformed vectors 풙′, 풚′, 풛′ in the following way: ′ 풙 = (1 + 휖푥푥)풙̂ + 휖푥푦풚̂ + 휖푥푧풛̂ ′ 풚 = 휖푦푥풙̂ + (1 + 휖푦푦)풚̂ + 휖푦푧풛̂ ′ 풛 = 휖푧푥풙̂ + 휖푧푦풚̂ + (1 + 휖푧푧)풛̂ The components 휖훼훽 define the deformation. They are dimensionless and have values much smaller than 1 in most instances in solid state physics. How one ‘reads’ these vectors is (for example) 휖푥푥force along x, deformation along x; 휖푥푦shear xy-plane along x or y direction (depending which unit vector it is next to) The new axes have new lengths given by (for example): ′ ′ 2 2 2 풙 ∙ 풙 = 1 + 2휖푥푥 + 휖푥푥 + 휖푥푦 + 휖푥푧 Usually we are dealing with tiny deformations so 2nd order terms are often dropped. Deformation also changes the volume of a solid. Considering our unit cube, originally it had a volume of 1. After distortion, it has volume 1 + 휖푥푥 휖푥푦 휖푥푧 ′ ′ ′ ′ 푉 = 풙 ∙ 풚 × 풛 = | 휖푦푥 1 + 휖푦푦 휖푦푧 | ≈ 1 + 휖푥푥 + 휖푦푦 + 휖푧푧 휖푧푥 휖푧푦 1 + 휖푧푧 Dilation (훿) is given by: 푉 − 푉′ 훿 ≡ ≅ 휖 + 휖 + 휖 푉 푥푥 푦푦 푧푧 (2nd order terms have been dropped because we are working in a regime of small distortion which is almost always the appropriate one for solid state physics.
    [Show full text]
  • Simple Harmonic Motion
    [SHIVOK SP211] October 30, 2015 CH 15 Simple Harmonic Motion I. Oscillatory motion A. Motion which is periodic in time, that is, motion that repeats itself in time. B. Examples: 1. Power line oscillates when the wind blows past it 2. Earthquake oscillations move buildings C. Sometimes the oscillations are so severe, that the system exhibiting oscillations break apart. 1. Tacoma Narrows Bridge Collapse "Gallopin' Gertie" a) http://www.youtube.com/watch?v=j‐zczJXSxnw II. Simple Harmonic Motion A. http://www.youtube.com/watch?v=__2YND93ofE Watch the video in your spare time. This professor is my teaching Idol. B. In the figure below snapshots of a simple oscillatory system is shown. A particle repeatedly moves back and forth about the point x=0. Page 1 [SHIVOK SP211] October 30, 2015 C. The time taken for one complete oscillation is the period, T. In the time of one T, the system travels from x=+x , to –x , and then back to m m its original position x . m D. The velocity vector arrows are scaled to indicate the magnitude of the speed of the system at different times. At x=±x , the velocity is m zero. E. Frequency of oscillation is the number of oscillations that are completed in each second. 1. The symbol for frequency is f, and the SI unit is the hertz (abbreviated as Hz). 2. It follows that F. Any motion that repeats itself is periodic or harmonic. G. If the motion is a sinusoidal function of time, it is called simple harmonic motion (SHM).
    [Show full text]
  • 19.1 Attitude Determination and Control Systems Scott R. Starin
    19.1 Attitude Determination and Control Systems Scott R. Starin, NASA Goddard Space Flight Center John Eterno, Southwest Research Institute In the year 1900, Galveston, Texas, was a bustling direct hit as Ike came ashore. Almost 200 people in the community of approximately 40,000 people. The Caribbean and the United States lost their lives; a former capital of the Republic of Texas remained a tragedy to be sure, but far less deadly than the 1900 trade center for the state and was one of the largest storm. This time, people were prepared, having cotton ports in the United States. On September 8 of received excellent warning from the GOES satellite that year, however, a powerful hurricane struck network. The Geostationary Operational Environmental Galveston island, tearing the Weather Bureau wind Satellites have been a continuous monitor of the gauge away as the winds exceeded 100 mph and world’s weather since 1975, and they have since been bringing a storm surge that flooded the entire city. The joined by other Earth-observing satellites. This weather worst natural disaster in United States’ history—even surveillance to which so many now owe their lives is today—the hurricane caused the deaths of between possible in part because of the ability to point 6000 and 8000 people. Critical in the events that led to accurately and steadily at the Earth below. The such a terrible loss of life was the lack of precise importance of accurately pointing spacecraft to our knowledge of the strength of the storm before it hit. daily lives is pervasive, yet somehow escapes the notice of most people.
    [Show full text]
  • Crack Tip Elements and the J Integral
    EN234: Computational methods in Structural and Solid Mechanics Homework 3: Crack tip elements and the J-integral Due Wed Oct 7, 2015 School of Engineering Brown University The purpose of this homework is to help understand how to handle element interpolation functions and integration schemes in more detail, as well as to explore some applications of FEA to fracture mechanics. In this homework you will solve a simple linear elastic fracture mechanics problem. You might find it helpful to review some of the basic ideas and terminology associated with linear elastic fracture mechanics here (in particular, recall the definitions of stress intensity factor and the nature of crack-tip fields in elastic solids). Also check the relations between energy release rate and stress intensities, and the background on the J integral here. 1. One of the challenges in using finite elements to solve a problem with cracks is that the stress field at a crack tip is singular. Standard finite element interpolation functions are designed so that stresses remain finite a everywhere in the element. Various types of special b c ‘crack tip’ elements have been designed that 3L/4 incorporate the singularity. One way to produce a L/4 singularity (the method used in ABAQUS) is to mesh L the region just near the crack tip with 8 noded elements, with a special arrangement of nodal points: (i) Three of the nodes (nodes 1,4 and 8 in the figure) are connected together, and (ii) the mid-side nodes 2 and 7 are moved to the quarter-point location on the element side.
    [Show full text]
  • Beam Element Stiffness Matrices
    Beam Element Stiffness Matrices CEE 421L. Matrix Structural Analysis Department of Civil and Environmental Engineering Duke University Henri P. Gavin Fall, 2014 Truss elements carry only axial forces. Beam elements carry shear forces and bending moments. Frame elements carry shear forces, bending moments, and axial forces. This document presents the development of beam element stiffness matrices in local coordinates. 1 A simply supported beam carrying end-moments Consider a simply supported beam resisting moments M1 and M2 applied at its ends. The flexibility relates the end rotations {θ1, θ2} to the end moments {M1,M2}: θ1 F11 F12 M1 = . θ2 F21 F22 M2 The flexibility coefficients, Fij, may be obtained from Castigliano’s 2nd Theo- ∗ rem, θi = ∂U (Mi)/∂Mi. First Column Second Column 2 CEE 421L. Matrix Structural Analysis – Duke University – Fall 2014 – H.P. Gavin The applied moments M1 and M2 are in equilibrium with the reactions forces V1 and V2; V1 = (M1 + M2)/L and V2 = −(M1 + M2)/L M + M x ! x V (x) = 1 2 M(x) = M − 1 + M L 1 L 2 L The total potential energy of a beam with these forces and moments is: 1Z L M 2 1Z L V 2 U = dx + dx 2 0 EI 2 0 G(A/α) By Castigliano’s Theorem, ∂U θ1 = ∂M1 ∂M(x) ∂V (x) Z L M(x) Z L V (x) = ∂M1 dx + ∂M1 dx 0 EI 0 G(A/α) x 2 x x Z L Z L Z L Z L L − 1 dx αdx L L − 1 dx αdx = + M1 + + M2 0 EI 0 GAL2 0 EI 0 GAL2 and ∂U θ2 = ∂M2 ∂M(x) ∂V (x) Z L M(x) Z L V (x) = ∂M2 dx + ∂M2 dx 0 EI 0 G(A/α) x x x 2 Z L Z L Z L Z L L L − 1 dx αdx L dx αdx = + M1 + + M2 0 EI 0 GAL2 0 EI 0 GAL2
    [Show full text]
  • Introduction to Stiffness Analysis Stiffness Analysis Procedure
    Introduction to Stiffness Analysis displacements. The number of unknowns in the stiffness method of The stiffness method of analysis is analysis is known as the degree of the basis of all commercial kinematic indeterminacy, which structural analysis programs. refers to the number of node/joint Focus of this chapter will be displacements that are unknown development of stiffness equations and are needed to describe the that only take into account bending displaced shape of the structure. deformations, i.e., ignore axial One major advantage of the member, a.k.a. slope-deflection stiffness method of analysis is that method. the kinematic degrees of freedom In the stiffness method of analysis, are well-defined. we write equilibrium equations in 1 2 terms of unknown joint (node) Definitions and Terminology Stiffness Analysis Procedure Positive Sign Convention: Counterclockwise moments and The steps to be followed in rotations along with transverse forces and displacements in the performing a stiffness analysis can positive y-axis direction. be summarized as: 1. Determine the needed displace- Fixed-End Forces: Forces at the “fixed” supports of the kinema- ment unknowns at the nodes/ tically determinate structure. joints and label them d1, d2, …, d in sequence where n = the Member-End Forces: Calculated n forces at the end of each element/ number of displacement member resulting from the unknowns or degrees of applied loading and deformation freedom. of the structure. 3 4 1 2. Modify the structure such that it fixed-end forces are vectorially is kinematically determinate or added at the nodes/joints to restrained, i.e., the identified produce the equivalent fixed-end displacements in step 1 all structure forces, which are equal zero.
    [Show full text]
  • Fundamentals of Biomechanics Duane Knudson
    Fundamentals of Biomechanics Duane Knudson Fundamentals of Biomechanics Second Edition Duane Knudson Department of Kinesiology California State University at Chico First & Normal Street Chico, CA 95929-0330 USA [email protected] Library of Congress Control Number: 2007925371 ISBN 978-0-387-49311-4 e-ISBN 978-0-387-49312-1 Printed on acid-free paper. © 2007 Springer Science+Business Media, LLC All rights reserved. This work may not be translated or copied in whole or in part without the written permission of the publisher (Springer Science+Business Media, LLC, 233 Spring Street, New York, NY 10013, USA), except for brief excerpts in connection with reviews or scholarly analysis. Use in connection with any form of information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed is forbidden. The use in this publication of trade names, trademarks, service marks and similar terms, even if they are not identified as such, is not to be taken as an expression of opinion as to whether or not they are subject to proprietary rights. 987654321 springer.com Contents Preface ix NINE FUNDAMENTALS OF BIOMECHANICS 29 Principles and Laws 29 Acknowledgments xi Nine Principles for Application of Biomechanics 30 QUALITATIVE ANALYSIS 35 PART I SUMMARY 36 INTRODUCTION REVIEW QUESTIONS 36 CHAPTER 1 KEY TERMS 37 INTRODUCTION TO BIOMECHANICS SUGGESTED READING 37 OF UMAN OVEMENT H M WEB LINKS 37 WHAT IS BIOMECHANICS?3 PART II WHY STUDY BIOMECHANICS?5 BIOLOGICAL/STRUCTURAL BASES
    [Show full text]
  • Cross-Linked Polymers and Rubber Elasticity Chapter 9 (Sperling)
    Cross-linked Polymers and Rubber Elasticity Chapter 9 (Sperling) • Definition of Rubber Elasticity and Requirements • Cross-links, Networks, Classes of Elastomers (sections 1-3, 16) • Simple Theory of Rubber Elasticity (sections 4-8) – Entropic Origin of Elastic Retractive Forces – The Ideal Rubber Behavior • Departures from the Ideal Rubber Behavior (sections 9-11) – Non-zero Energy Contribution to the Elastic Retractive Forces – Stress-induced Crystallization and Limited Extensibility of Chains (How to make better elastomers: High Strength and High Modulus) – Network Defects (dangling chains, loops, trapped entanglements, etc..) – Semi-empirical Mooney-Rivlin Treatment (Affine vs Non-Affine Deformation) Definition of Rubber Elasticity and Requirements • Definition of Rubber Elasticity: Very large deformability with complete recoverability. • Molecular Requirements: – Material must consist of polymer chains. Need to change conformation and extension under stress. – Polymer chains must be highly flexible. Need to access conformational changes (not w/ glassy, crystalline, stiff mat.) – Polymer chains must be joined in a network structure. Need to avoid irreversible chain slippage (permanent strain). One out of 100 monomers must connect two different chains. Connections (covalent bond, crystallite, glassy domain in block copolymer) Cross-links, Networks and Classes of Elastomers • Chemical Cross-linking Process: Sol-Gel or Percolation Transition • Gel Characteristics: – Infinite Viscosity – Non-zero Modulus – One giant Molecule – Solid
    [Show full text]
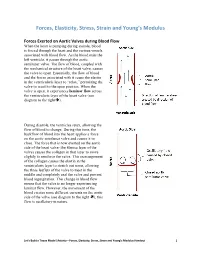
  • Forces, Elasticity, Stress, Strain and Young's Modulus Handout
    Forces, Elasticity, Stress, Strain and Young’s Modulus Forces Exerted on Aortic Valves during Blood Flow When the heart is pumping during systole, blood is forced through the heart and the various vessels associated with blood flow. As the blood exits the left ventricle, it passes through the aortic semilunar valve. The flow of blood, coupled with the mechanical structure of the heart valve, causes the valve to open. Essentially, the flow of blood and the forces associated with it cause the elastin in the ventricularis layer to “relax,” permitting the valve to recoil to the open position. When the valve is open, it experiences laminar flow across the ventricularis layer of the heart valve (see diagram to the right). During diastole, the ventricles relax, allowing the flow of blood to change. During this time, the backflow of blood into the heart applies a force on the aortic semilunar valve and causes it to close. The force that is now exerted on the aortic side of the heart valve (the fibrosa layer of the valve) causes the collagen in that layer to move slightly to reinforce the valve. This rearrangement of the collagen causes the elastin in the ventricularis layer to stretch out some, allowing the three leaflets of the valve to meet in the middle and completely seal the valve and prevent blood regurgitation. This change in blood flow means that the valve is no longer experiencing laminar flow. However, the movement of the blood creates some different currents on the aortic side of the valve (see diagram to the right ); this flow is oscillatory in nature.
    [Show full text]
  • The Effect of Spring Mass on the Oscillation Frequency
    The Effect of Spring Mass on the Oscillation Frequency Scott A. Yost University of Tennessee February, 2002 The purpose of this note is to calculate the effect of the spring mass on the oscillation frequency of an object hanging at the end of a spring. The goal is to find the limitations to a frequently-quoted rule that 1/3 the mass of the spring should be added to to the mass of the hanging object. This calculation was prompted by a student laboratory exercise in which it is normally seen that the frequency is somewhat lower than this rule would predict. Consider a mass M hanging from a spring of unstretched length l, spring constant k, and mass m. If the mass of the spring is neglected, the oscillation frequency would be ω = k/M. The quoted rule suggests that the effect of the spring mass would beq to replace M by M + m/3 in the equation for ω. This result can be found in some introductory physics textbooks, including, for example, Sears, Zemansky and Young, University Physics, 5th edition, sec. 11-5. The derivation assumes that all points along the spring are displaced linearly from their equilibrium position as the spring oscillates. This note will examine more general cases for the masses, including the limit M = 0. An appendix notes how the linear oscillation assumption breaks down when the spring mass becomes large. Let the positions along the unstretched spring be labeled by x, running from 0 to L, with 0 at the top of the spring, and L at the bottom, where the mass M is hanging.
    [Show full text]
  • Glossary of Materials Engineering Terminology
    Glossary of Materials Engineering Terminology Adapted from: Callister, W. D.; Rethwisch, D. G. Materials Science and Engineering: An Introduction, 8th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, 2010. McCrum, N. G.; Buckley, C. P.; Bucknall, C. B. Principles of Polymer Engineering, 2nd ed.; Oxford University Press: New York, NY, 1997. Brittle fracture: fracture that occurs by rapid crack formation and propagation through the material, without any appreciable deformation prior to failure. Crazing: a common response of plastics to an applied load, typically involving the formation of an opaque banded region within transparent plastic; at the microscale, the craze region is a collection of nanoscale, stress-induced voids and load-bearing fibrils within the material’s structure; craze regions commonly occur at or near a propagating crack in the material. Ductile fracture: a mode of material failure that is accompanied by extensive permanent deformation of the material. Ductility: a measure of a material’s ability to undergo appreciable permanent deformation before fracture; ductile materials (including many metals and plastics) typically display a greater amount of strain or total elongation before fracture compared to non-ductile materials (such as most ceramics). Elastic modulus: a measure of a material’s stiffness; quantified as a ratio of stress to strain prior to the yield point and reported in units of Pascals (Pa); for a material deformed in tension, this is referred to as a Young’s modulus. Engineering strain: the change in gauge length of a specimen in the direction of the applied load divided by its original gauge length; strain is typically unit-less and frequently reported as a percentage.
    [Show full text]