DOCSLIB.ORG

Chapter 9B -- Conservation of Momentum

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter 9B -- Conservation of Momentum ChapterChapter 9B9B -- ConservationConservation ofof MomentumMomentum AAA PowerPointPowerPointPowerPoint PresentationPresentationPresentation bybyby PaulPaulPaul E.E.E. Tippens,Tippens,Tippens, EmeritusEmeritusEmeritus ProfessorProfessorProfessor SouthernSouthernSouthern PolytechnicPolytechnicPolytechnic StateStateState UniversityUniversityUniversity © 2007 Momentum is conserved in this rocket launch. The velocity of the rocket and its payload is determined by the mass and velocity of the expelled gases. Photo: NASA NASA Objectives:Objectives: AfterAfter completingcompleting thisthis module,module, youyou shouldshould bebe ableable to:to: •• StateState thethe lawlaw ofof conservationconservation ofof momentummomentum andand applyapply itit toto thethe solutionsolution ofof problems.problems. •• DistinguishDistinguish byby definitiondefinition andand exampleexample betweenbetween elasticelastic andand inelasticinelastic collisions.collisions. •• PredictPredict thethe velocitiesvelocities ofof twotwo collidingcolliding bodiesbodies whenwhen givengiven thethe coefficientscoefficients ofof restitution,restitution, masses,masses, andand initialinitial velocities.velocities. AA CollisionCollision ofof TwoTwo MassesMasses When two masses m1 and m2 collide, we will use the symbol u to describe velocities before collision. BeforeBefore u1 u2 m1 m2 The symbol v will describe velocities after collision. v AfterAfter v 1 m 2 m1 2 AA CollisionCollision ofof TwoTwo BlocksBlocks BeforeBefore u1 u2 m1 m2 Collision “u”= Before “v” = After m1 m2B AfterAfter v1 m v2 m1 2 ConservationConservation ofof EnergyEnergy u u1 2 m1 m2 The kinetic energy beforebefore colliding is equal to the kinetic energy afterafter colliding plus the energy lostlost in the collision. 112222 11 22mu11 mu 2 2 22 mv 11 mv 22 Loss ExampleExample 1.1. AA 22--kgkg massmass movingmoving atat 44 m/sm/s collidescollides withwith aa 11--kgkg massmass initiallyinitially atat rest.rest. AfterAfter thethe collision,collision, thethe 22--kgkg massmass movesmoves atat 11 m/sm/s andand thethe 11--kgkg massmass movesmoves atat 33 m/sm/s.. WhatWhat energyenergy waswas lostlost inin thethe collision?collision? ItIt’’ss importantimportant toto drawdraw andand labellabel aa sketchsketch withwith appropriateappropriate symbolssymbols andand givengiven information.information. u = 0 u1 = 4 m/s 2 v1 = 1 m/s v2 = 2 m/s m1 m2 m1 m2 m1 = 2 kg m1 = 1 kg m1 = 2 kg m1 = 1 kg BEFOREBEFORE AFTERAFTER ExampleExample 11 (Continued).(Continued). WhatWhat energyenergy waswas lostlost inin thethe collision?collision? EnergyEnergy isis conserved.conserved. u = 0 u1 = 4 m/s 2 v1 = 1 m/s v2 = 2 m/s m1 m2 m1 m2 m1 = 2 kg m1 = 1 kg m1 = 2 kg m1 = 1 kg 1122 1 2 BEFORE:BEFORE: 22mu11 mu 2 2 2(2 kg)(4 m/s) 0 16 J 1122 1 21 2 AFTERAFTER22mv11 mv 2 2 2(2 kg)(1 m/s) 2 (1 kg)(2 m/s) 3 J Energy Conservation: K(Before) = K(After) + Loss Loss = 16 J – 3 J EnergyEnergy LossLoss == 1515 JJ ImpulseImpulse andand MomentumMomentum u uA B A B Impulse = p --FF tt FF tt Ft= mv–mv A B B f o Opposite but Equal F t vA v A B B FB t= -FA t mB vB -mB uB = -(mA vA -mA uA ) Simplifying: m v + m v = m u + m u mAA vAA + mBB vBB = mAA uAA + mBB uBB ConservationConservation ofof MomentumMomentum The total momentum AFTER a collision is equal to the total momentum BEFORE. m v + m v = m u + m u mAA vAA + mBB vBB = mAA uAA + mBB uBB u uB A A B Recall that the total energy is also conserved: --FF tt FF tt A B B KineticKinetic Energy:Energy: KK == ½½mvmv2 vA v B KK ++ KK == KK ++ KK ++ LossLoss A B KA0A0 + KB0B0 = KAfAf + KBfBf + Loss ExampleExample 2:2: AA 22--kgkg blockblock AA andand aa 11--kgkg blockblock BB areare pushedpushed togethertogether againstagainst aa springspring andand tiedtied withwith aa cord.cord. WhenWhen thethe cordcord breaks,breaks, thethe 11--kgkg blockblock movesmoves toto thethe rightright atat 88 m/sm/s.. WhatWhat isis thethe velocityvelocity ofof thethe 22 kgkg block?block? TheThe initialinitial velocitiesvelocities areare zerozero,, soso thatthat thethe totaltotal A B momentummomentum beforebefore releaserelease isis zero.zero. 0 0 mmA vvA ++ mmB vvB == mmA uuA ++ mmB uuB mB vB mA vA = - mB vB vA = - mA ExampleExample 22 (Continued)(Continued) 2 kg vA2 8 m/s 1 kg A B A B 0 0 mmA vvA ++ mmB vvB == mmA uuA ++ mmB uuB mB vB mA vA = - mB vB vA = - mA (1 kg)(8 m/s) v = - vvA == --44 m/sm/s A (2 kg) A ExampleExample 22 (Cont.):(Cont.): IgnoringIgnoring friction,friction, howhow muchmuch energyenergy waswas releasedreleased byby thethe spring?spring? 2 kg 4 m/s 8 m/s 1 kg A B A B 2 2 2 Cons. of E: ½½kxkx == ½½mmA vvA ++ ½½mmB vvB ½½kxkx2 == ½½(2(2 kg)(4kg)(4 m/s)m/s)2 ++ ½½(1(1 kg)(8kg)(8 m/s)m/s)2 ½½kxkx2 == 1616 JJ ++ 3232 JJ == 4848 JJ ½½kxkx22 == 4848 JJ ElasticElastic oror Inelastic?Inelastic? An elastic collision loses In an inelastic collision, no energy. The deform- energy is lost and the ation on collision is fully deformation may be restored. permanent. (Click it.) CompletelyCompletely InelasticInelastic CollisionsCollisions CollisionsCollisions wherewhere twotwo objectsobjects stickstick togethertogether andand havehave aa commoncommon velocityvelocity afterafter impact.impact. Before After ExampleExample 3:3: AA 6060--kgkg footballfootball playerplayer standsstands onon aa frictionlessfrictionless lakelake ofof ice.ice. HeHe catchescatches aa 22--kgkg footballfootball andand thenthen movesmoves atat 4040 cm/scm/s.. WhatWhat waswas thethe initialinitial velocityvelocity ofof thethe football?football? A Given: uB = 0; mA = 2 kg; mB = 60 kg; B vA = vB = vC vC = 0.4 m/s 0 Momentum: mmA vvA ++ mmB vvB == mmA uuA ++ mmB uuB Inelastic collision: (m(mA ++ mmB )v)vC == mmA uuA (2 kg + 60 kg)(0.4 m/s) = (2 kg)uA u == 12.412.4 m/sm/s uuAA = 12.4 m/s ExampleExample 33 (Cont.):(Cont.): HowHow muchmuch energyenergy waswas lostlost inin catchingcatching thethe football?football? 0 1122 1 2 22muAA mu BB 2()Loss m A m B v C ½(2 kg)(12.4 m/s)2 = ½(62 kg)(0.4 m/s)2 + Loss 154 J = 4.96 J + Loss LossLossLoss === 149149149 JJJ 97% of the energy is lost in the collision!! General:General: CompletelyCompletely InelasticInelastic Collisions where two objects stick together and have a common velocity vC after impact. ConservationConservation ofof Momentum:Momentum: ()mmvmumuA Bc AA BB ConservationConservation ofof Energy:Energy: 1122 1 2 22muAA mu BB 2() m A m B v c Loss ExampleExample 4.4. AnAn 8787--kgkg skaterskater BB collidescollides withwith aa 2222--kgkg skaterskater AA initiallyinitially atat restrest onon ice.ice. TheyThey movemove togethertogether afterafter thethe collisioncollision atat 2.42.4 m/sm/s.. FindFind thethe velocityvelocity ofof thethe skaterskater BB beforebefore thethe collision.collision. Common speed after vvB == vvA == vvC == 2.42.4 m/sm/s colliding: 2.4 m/s. uuA = 0 uuB = ? muA ABBABC mu() m m v 87 kg (87 kg)u = (87 kg + 22 kg)(2.4 m/s) BB uB AA 22 kg (87(87 kg)kg)uuB =262=262 kgkg m/sm/s uB = 3.01 m/s ExampleExample 5:5: AA 5050 gg bulletbullet strikesstrikes aa 11--kgkg block,block, passespasses allall thethe wayway through,through, thenthen lodgeslodges intointo thethe 22 kgkg block.block. Afterward,Afterward, thethe 11 kgkg blockblock movesmoves atat 11 m/sm/s andand thethe 22 kgkg blockblock movesmoves atat 22 m/sm/s.. WhatWhat waswas thethe entranceentrance velocityvelocity ofof thethe bullet?bullet? 2 kg uA = ? 1 kg 1 m/s 2 m/s 1 kg 2 kg A C B Find entrance velocity of 50 g 1 kg 2 kg bullet: mA = 0.05 kg; uA = ? 1 m/s 2 m/s Momentum After = 1 kg 2 kg Momentum Before 0 0 mA uA + mB uB + mCu C = mB vB + (mA +mC) vAC (0.05 kg)uuA =(1 kg)(1 m/s)+(2.052.05 kgkg)(2 m/s) (0.05 kg) uuA =(5.1 kg m/s) u = 102 m/s uAA = 102 m/s CompletelyCompletely ElasticElastic CollisionsCollisions Collisions where two objects collide in such a way that zero energy is lost in the process. APPROXIMATIONS!APPROXIMATIONS! VelocityVelocity inin ElasticElastic CollisionsCollisions uA uB A B 1. Zero energy lost. 2. Masses do not change. vA vB A B 3. Momentum conserved. Equal but opposite impulses (F t) means that: (Relative v After) = - (Relative v Before) For elastic collisions: v -v = - (u -u ) vAA -vBB = - (uAA -uBB ) ExampleExample 6:6: AA 22--kgkg ballball movingmoving toto thethe rightright atat 11 m/sm/s strikesstrikes aa 44--kgkg ballball movingmoving leftleft atat 33 m/sm/s.. WhatWhat areare thethe velocitiesvelocities afterafter impact,impact, assumingassuming completecomplete elasticity?elasticity? 1 m/s 3 m/s vvA -- vvB == -- ((uuA -- uuB) ) A B vv -- vv == uu -- uu 1 kg 2 kg A B B A vvA vvB A B vvA -- vvB = (-3 m/s) - (1 m/s) From conservation of energy (relative v): v -v = -4 m/s vAA -vBB = -4 m/s ExampleExample 66 (Continued)(Continued) 1 m/s 3 m/s Energy:Energy: vvA -- vvB == -- 44 m/sm/s A B Momentum also conserved: vv 1 kg 2 kg vv A A B B mmA vvA ++ mmB vvB == mmA uuA ++ mmB uuB (1 kg)vvA +(2 kg)vvB =(1 kg)(1 m/s)+(2 kg)(-3 m/s) Two independent vvA ++ 2v2vB = -5 m/s equations to solve: vvA -- vvB == -- 44 m/sm/s ExampleExample 66 (Continued)(Continued) 1 m/s 3 m/s vA + 2vB = -5 m/s A B vvA -- vvB == -- 44 m/sm/s vv 1 kg 2 kg vv A A B B Subtract: 0 + 3vv B2 == -- 11 m/sm/s vvB == -- 0.3330.333 m/sm/s B vv A2 -- ((--0.3330.333 m/s)m/s) == -- 44 m/sm/s Substitution: v = -3.67 m/s vAA = -3.67 m/s vvA -- vvB == -- 44 m/sm/s Example 7.
Load more

Recommended publications
  • 10-1 CHAPTER 10 DEFORMATION 10.1 Stress-Strain Diagrams And
    EN380 Naval Materials Science and Engineering Course Notes, U.S. Naval Academy CHAPTER 10 DEFORMATION 10.1 Stress-Strain Diagrams and Material Behavior 10.2 Material Characteristics 10.3 Elastic-Plastic Response of Metals 10.4 True stress and strain measures 10.5 Yielding of a Ductile Metal under a General Stress State - Mises Yield Condition. 10.6 Maximum shear stress condition 10.7 Creep Consider the bar in figure 1 subjected to a simple tension loading F. Figure 1: Bar in Tension Engineering Stress () is the quotient of load (F) and area (A). The units of stress are normally pounds per square inch (psi). = F A where: is the stress (psi) F is the force that is loading the object (lb) A is the cross sectional area of the object (in2) When stress is applied to a material, the material will deform. Elongation is defined as the difference between loaded and unloaded length ∆푙 = L - Lo where: ∆푙 is the elongation (ft) L is the loaded length of the cable (ft) Lo is the unloaded (original) length of the cable (ft) 10-1 EN380 Naval Materials Science and Engineering Course Notes, U.S. Naval Academy Strain is the concept used to compare the elongation of a material to its original, undeformed length. Strain () is the quotient of elongation (e) and original length (L0). Engineering Strain has no units but is often given the units of in/in or ft/ft. ∆푙 휀 = 퐿 where: is the strain in the cable (ft/ft) ∆푙 is the elongation (ft) Lo is the unloaded (original) length of the cable (ft) Example Find the strain in a 75 foot cable experiencing an elongation of one inch.
    [Show full text]
  • Milton's Use of the Epic Simile in Paradise Lost
    Loyola University Chicago Loyola eCommons Master's Theses Theses and Dissertations 1941 Milton's Use of the Epic Simile in Paradise Lost Francis Louis Martinsek Loyola University Chicago Follow this and additional works at: https://ecommons.luc.edu/luc_theses Part of the English Language and Literature Commons Recommended Citation Martinsek, Francis Louis, "Milton's Use of the Epic Simile in Paradise Lost" (1941). Master's Theses. 289. https://ecommons.luc.edu/luc_theses/289 This Thesis is brought to you for free and open access by the Theses and Dissertations at Loyola eCommons. It has been accepted for inclusion in Master's Theses by an authorized administrator of Loyola eCommons. For more information, please contact [email protected]. This work is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 License. Copyright © 1941 Francis Louis Martinsek J3 MILTON'S USE OF THE EPIC SIMILE IN PARADISE -LOST by Francis Louis Martinsek, S.J. JUNE 1941 A THESIS SUBMITTED IN PARTIAL FULFILL~ffiNT OF THE REQUIREMENTS FOR THE DEGREE OF W~STER OF ARTS IN LOYOLA UNIVERSITY VITA AUCTORIS Francis L. ~~rtinsek, S.J., was born at Export, Pennsylvania, on November 12, 1912. He received his elementary training at Export Public Schools, and his high-school training at Export Junior High School and Trafford City High School. He entered Xavier University, Cincinnati, in 1932 and transferred to West Baden College of Loyola University in 1935, where he received his Bachelor of Arts degree in 1936. TABLE OF CONTENTS INTRODUCTION PAGE Purpose of Thesis; Method~ Procedure •••••••••••1 CHAPTER I The Familz ~~~Epic Simile •••••••••••••••~ CHAPTER II The Function£!~ Simile••••••••••••••••••••••!! CHAPTER III ~Epic Simile in Paradise Lost ••••••••••••••••~ CHAPTER IV The Epic Simile~ Milton's Style ••••••••••••••~ COl\fCLUSION •••••••••••••••••••••••••••••••••••••••••• •~ BIBLIOGRAPIIT • ••••••••••••••••••••••••••••••••••••••••§1_ L.D.S.
    [Show full text]
  • Crack Tip Elements and the J Integral
    EN234: Computational methods in Structural and Solid Mechanics Homework 3: Crack tip elements and the J-integral Due Wed Oct 7, 2015 School of Engineering Brown University The purpose of this homework is to help understand how to handle element interpolation functions and integration schemes in more detail, as well as to explore some applications of FEA to fracture mechanics. In this homework you will solve a simple linear elastic fracture mechanics problem. You might find it helpful to review some of the basic ideas and terminology associated with linear elastic fracture mechanics here (in particular, recall the definitions of stress intensity factor and the nature of crack-tip fields in elastic solids). Also check the relations between energy release rate and stress intensities, and the background on the J integral here. 1. One of the challenges in using finite elements to solve a problem with cracks is that the stress field at a crack tip is singular. Standard finite element interpolation functions are designed so that stresses remain finite a everywhere in the element. Various types of special b c ‘crack tip’ elements have been designed that 3L/4 incorporate the singularity. One way to produce a L/4 singularity (the method used in ABAQUS) is to mesh L the region just near the crack tip with 8 noded elements, with a special arrangement of nodal points: (i) Three of the nodes (nodes 1,4 and 8 in the figure) are connected together, and (ii) the mid-side nodes 2 and 7 are moved to the quarter-point location on the element side.
    [Show full text]
  • EVALUATION of a COLLISION AVOIDANCE and MITIGATION SYSTEM (CAMS) on WINTER MAINTENANCE TRUCKS Research Administration Reference Number: OR17-103
    EVALUATION OF A COLLISION AVOIDANCE AND MITIGATION SYSTEM (CAMS) ON WINTER MAINTENANCE TRUCKS Research Administration Reference Number: OR17-103 Prepared for Michigan Department of Transportation Division of Research 8885 Ricks Road Lansing, MI 48917 Prepared by Michigan State University Department of Civil and Environmental Engineering 428 South Shaw Lane East Lansing, MI 48824 Institute for Transportation Iowa State University 2711 South Loop Drive, Suite 4700 Ames, IA 50010 FreezePoint Consulting 179 University Circle Akron, OH SEPTEMBER 21, 2018 Technical Report Documentation Page 1. Report No. 2. Government Accession No. 3. MDOT Project Manager OR 17-103 N/A Steven J. Cook, P.E. 4. Title and Subtitle 5. Report Date EVALUATION OF A COLLISION AVOIDANCE AND MITIGATION September 21, 2018 SYSTEM (CAMS) ON WINTER MAINTENANCE TRUCKS 6. Performing Organization Code N/A 7. Author(s) 8. Performing Organization Report No. Ali Zockaie, Ramin Saedi, Timothy Gates, Peter Savolainen, Bill Schneider, N/A Mehrnaz Ghamami, Rajat Verma, Fatemeh Fakhrmoosavi, Mohammad Kavianipour, MohammadHossein (Sam) Shojaei, Harprinderjot Singh, Jacob Warner, and Chao Zhou 9. Performing Organization Name and Address 10. Work Unit No. (TRAIS) Michigan State University N/A 428 S. Shaw Lane 11. Contract or Grant No. East Lansing, Michigan 48824 2018-0060 11 (a). Authorization No. 12. Sponsoring Organization Name and Address 13. Type of Report and Period Covered Michigan Department of Transportation Final Report Research Administration 10/01/2017 to 09/30/2018 8885 Ricks Rd. P.O. Box 30049 14. Sponsoring Agency Code Lansing, Michigan 48909 N/A 15. Supplementary Notes Conducted in cooperation with the U.S. Department of Transportation, Federal Highway Administration.
    [Show full text]
  • Kentucky Traffic Collision Facts Report Includes a Lot of Vital Information and Statistics Regarding Auto Collisions That Occurred on Our Commonwealth’S Roadways
    2019 REPORT Do you need access to data or advice from a traffic safety expert? If you’d like to ask for help with your project, check out the Kentucky Traffic Data Services. KTSDS.ktc.uky.edu Photos and other images created by the Kentucky Transportation Center or licensed with credits under a standard perpetual license agreement through iStock.com in partnership with Getty Images(US), Inc. Dear Kentuckians: Being transparent is a top priority for my administration, and one way to be transparent is to share available data. The 2019 Kentucky Traffic Collision Facts report includes a lot of vital information and statistics regarding auto collisions that occurred on our commonwealth’s roadways. This report should serve as a reminder to all of us that it is our individual responsibility every time we get behind the wheel to demonstrate the skill and knowledge of safe driving in order to keep ourselves and our fellow Kentuckians safe from harm while operating a vehicle. Unfortunately, I am sad to report our commonwealth lost 732 Kentuckians in 2019 to auto collisions; of which 289 were under the influence of drugs and 135 were under the influence of alcohol. They are people who are truly missed by their family and their friends. These lives lost should reinforce our resolve to do our best every day to protect those around us on the roadways. I want to remind all motorists whether they are new to the road or a seasoned driver to follow these safe practices: • Never text and drive • Don’t operate a vehicle under the influence of any substance • Always buckle up • Observe speed limits By holding ourselves accountable and working together, we will save lives and make our roadways safer for all Kentuckians and visitors to our great commonwealth.
    [Show full text]
  • UAS Ground Collision Severity Evaluation Revision 2
    Final Report for the FAA UAS Center of Excellence Task A4: UAS Ground Collision Severity Evaluation Revision 2 Mr. David Arterburn, Principal Investigator – [email protected] Director, Rotorcraft Systems Engineering and Simulation Center The University of Alabama in Huntsville Dr. Mark Ewing – [email protected] Associate Professor and Director of the Flight Research Laboratory The University of Kansas Dr. Raj Prabhu – [email protected] Professor, Department of Agricultural and Biological Engineering Mississippi State University Dr. Feng Zhu – [email protected] Assistant Professor, Mechanical Engineering Department Embry-Riddle Aeronautical University Dr. David Francis – [email protected] Post-Doctoral Researcher, Center for Advanced Vehicular Systems Mississippi State University SECURITY STATEMENT: There is no classified or proprietary information in this report. DISTRIBUTION A: Distribution is unlimited 1 Legal Disclaimer The information provided herein may include content supplied by third parties. Although the data and information contained herein has been produced or processed from sources believed to be reliable, the Federal Aviation Administration makes no warranty, expressed or implied, regarding the accuracy, adequacy, completeness, legality, reliability or usefulness of any information, conclusions or recommendations provided herein. Distribution of the information contained herein does not constitute an endorsement or warranty of the data or information provided herein by the Federal Aviation Administration or the U.S. Department of Transportation. Neither the Federal Aviation Administration or the U.S. Department of Transportation shall be held liable for any improper or incorrect use of the information contained herein and assumes no responsibility for anyone’s use of the information. The Federal Aviation Administration and U.S.
    [Show full text]
  • A Framework of Optimizing Moose-Vehicle Collision Mitigation
    A Framework for Optimizing Moose-Vehicle Collision Mitigation Measures in Teton County WYDOT Sponsor Thomas Hart Wyoming Dept. of Transportation 5300 Bishop Boulevard Cheyenne, WY 82009 Phone: (307) 777-4495 WYDOT Co-Sponsor Bob Hammond, P.E. Wyoming Dept. of Transportation 1040 Evans Road Jackson, WY 83001 Phone: (307) 733-3665 Principal Investigator Corinna Riginos, Ph.D. Conservation Research Center (CRC) of Teton Science Schools (TSS) 700 Coyote Canyon Road Jackson, WY 83001 Phone: (307) 734-3741 Co-Investigators Doug Wachob, Ph.D., Associate Executive Director, TSS Kevin Krasnow, Ph.D., Research and Graduate Faculty, TSS Morgan Graham, GIS Manager, CRC Submitted: September 2013 Table of Contents Background and Rationale ..................................................................................................... 3 Introduction ....................................................................................................................... 3 The Role of Scale in Road Crossing Behavior and WVC Mitigation .................................. 5 Road Crossing Behavior in the Urban, Ex-Urban, and Rural Contexts ................................ 7 Study Benefits ....................................................................................................................... 7 Study Objectives .................................................................................................................... 9 Methods ................................................................................................................................
    [Show full text]
  • Terms and Conditions of Your Safety Connect Telematics Service
    Terms and Conditions of Your Toyota Entune Telematics Service Effective as of October 18th, 2017 Welcome to your Telematics Services, provided to you by Toyota, a division of Toyota Motor Sales, USA, Inc. (“Toyota”). These Terms and Conditions are a legal agreement between you and Toyota (“us”, “our”, and “we”). These Terms and Conditions are part of the Subscription Service Agreement (collectively, the “Agreement”). You can contact us at any time by calling Toyota at 1-800- 331-4331, by visiting www.toyota.com/support/contact.html and selecting the “Email” button, or by writing to us at Toyota, Toyota Entune Customer Care, P.O. Box 259001, Plano, TX 75025-9001. IN THIS AGREEMENT, WHEN WE USE THE WORDS “SAFETY CONNECT”, “TOYOTA ENTUNE” “TOYOTA ENTUNE REMOTE” OR “SERVICE(S)”, WE MEAN ALL THE SERVICES WE PROVIDE TO YOU UNDER YOUR SERVICE PLAN (“SERVICE PLAN”). UNLESS OTHERWISE STATED, ALL TERMS USED IN THESE TERMS AND CONDITIONS HAVE THE SAME MEANING AS SET FORTH IN THE SUBSCRIPTION SERVICE AGREEMENT. PLEASE READ THIS AGREEMENT BEFORE USING ANY SERVICE. It is your sole responsibility to make any of your passengers or drivers of your Vehicle aware of the data collection, use, sharing and retention terms of this Agreement. 1. STARTING YOUR SERVICE You can only get and use these Services by accepting this Agreement. To obtain these Services, your Vehicle must contain a factory installed Telematics System (the “System”). If you do not accept the Agreement, including these Terms and Conditions, please notify us immediately and we will cancel your Services. Failure to cancel your Services within 15 days of enrollment for the Services will be deemed acceptance of the Agreement, even if you have not signed the Subscription Services Agreement.
    [Show full text]
  • Cross-Linked Polymers and Rubber Elasticity Chapter 9 (Sperling)
    Cross-linked Polymers and Rubber Elasticity Chapter 9 (Sperling) • Definition of Rubber Elasticity and Requirements • Cross-links, Networks, Classes of Elastomers (sections 1-3, 16) • Simple Theory of Rubber Elasticity (sections 4-8) – Entropic Origin of Elastic Retractive Forces – The Ideal Rubber Behavior • Departures from the Ideal Rubber Behavior (sections 9-11) – Non-zero Energy Contribution to the Elastic Retractive Forces – Stress-induced Crystallization and Limited Extensibility of Chains (How to make better elastomers: High Strength and High Modulus) – Network Defects (dangling chains, loops, trapped entanglements, etc..) – Semi-empirical Mooney-Rivlin Treatment (Affine vs Non-Affine Deformation) Definition of Rubber Elasticity and Requirements • Definition of Rubber Elasticity: Very large deformability with complete recoverability. • Molecular Requirements: – Material must consist of polymer chains. Need to change conformation and extension under stress. – Polymer chains must be highly flexible. Need to access conformational changes (not w/ glassy, crystalline, stiff mat.) – Polymer chains must be joined in a network structure. Need to avoid irreversible chain slippage (permanent strain). One out of 100 monomers must connect two different chains. Connections (covalent bond, crystallite, glassy domain in block copolymer) Cross-links, Networks and Classes of Elastomers • Chemical Cross-linking Process: Sol-Gel or Percolation Transition • Gel Characteristics: – Infinite Viscosity – Non-zero Modulus – One giant Molecule – Solid
    [Show full text]
  • Chapter 10: Elasticity and Oscillations
    Chapter 10 Lecture Outline 1 Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Chapter 10: Elasticity and Oscillations •Elastic Deformations •Hooke’s Law •Stress and Strain •Shear Deformations •Volume Deformations •Simple Harmonic Motion •The Pendulum •Damped Oscillations, Forced Oscillations, and Resonance 2 §10.1 Elastic Deformation of Solids A deformation is the change in size or shape of an object. An elastic object is one that returns to its original size and shape after contact forces have been removed. If the forces acting on the object are too large, the object can be permanently distorted. 3 §10.2 Hooke’s Law F F Apply a force to both ends of a long wire. These forces will stretch the wire from length L to L+L. 4 Define: L The fractional strain L change in length F Force per unit cross- stress A sectional area 5 Hooke’s Law (Fx) can be written in terms of stress and strain (stress strain). F L Y A L YA The spring constant k is now k L Y is called Young’s modulus and is a measure of an object’s stiffness. Hooke’s Law holds for an object to a point called the proportional limit. 6 Example (text problem 10.1): A steel beam is placed vertically in the basement of a building to keep the floor above from sagging. The load on the beam is 5.8104 N and the length of the beam is 2.5 m, and the cross-sectional area of the beam is 7.5103 m2.
    [Show full text]
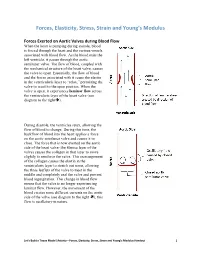
  • Forces, Elasticity, Stress, Strain and Young's Modulus Handout
    Forces, Elasticity, Stress, Strain and Young’s Modulus Forces Exerted on Aortic Valves during Blood Flow When the heart is pumping during systole, blood is forced through the heart and the various vessels associated with blood flow. As the blood exits the left ventricle, it passes through the aortic semilunar valve. The flow of blood, coupled with the mechanical structure of the heart valve, causes the valve to open. Essentially, the flow of blood and the forces associated with it cause the elastin in the ventricularis layer to “relax,” permitting the valve to recoil to the open position. When the valve is open, it experiences laminar flow across the ventricularis layer of the heart valve (see diagram to the right). During diastole, the ventricles relax, allowing the flow of blood to change. During this time, the backflow of blood into the heart applies a force on the aortic semilunar valve and causes it to close. The force that is now exerted on the aortic side of the heart valve (the fibrosa layer of the valve) causes the collagen in that layer to move slightly to reinforce the valve. This rearrangement of the collagen causes the elastin in the ventricularis layer to stretch out some, allowing the three leaflets of the valve to meet in the middle and completely seal the valve and prevent blood regurgitation. This change in blood flow means that the valve is no longer experiencing laminar flow. However, the movement of the blood creates some different currents on the aortic side of the valve (see diagram to the right ); this flow is oscillatory in nature.
    [Show full text]
  • Repair Facility Manual
    REPAIR FACILITY MANUAL Michigan Department of State Bureau of Regulatory Services Lansing, Michigan Secretary of State Bureau of Regulatory Services General Licensing Information Telephone 1-888-SOS-MICH (1-888-767-6424) Fax 517/335-2810 Business Licensing and Regulation Division Telephone 1-888-SOS-MICH (1-888-767-6424) Fax 517/335-2810 www.michigan.gov/sos January 2006 SOS-194 Table of Contents Page 1 Page TABLE OF CONTENTS INTRODUCTION.................................................................................................................1 IMPORTANT TELEPHONE NUMBERS............................................................3 CHAPTER 1: LICENSING REQUIREMENTS 1-1 Registering a Repair Facility ............................................................................................1 1-1.1 Requirement.......................................................................................................1 1-1.2 Exemptions ........................................................................................................1 1-1.3 Other Licensing Requirements ..........................................................................2 1-1.4 Loss of Registration ...........................................................................................2 1-1.5 Reporting Unlicensed Repair Facilities or Mechanics ......................................3 1-2 Registration Process ..........................................................................................................4 1-2.1 Procedure ...........................................................................................................4
    [Show full text]