DOCSLIB.ORG

Diapositive 1

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Diapositive 1 University of Liège Aerospace & Mechanical Engineering Fracture Mechanics, Damage and Fatigue Non Linear Fracture Mechanics: J-Integral Ludovic Noels Computational & Multiscale Mechanics of Materials – CM3 http://www.ltas-cm3.ulg.ac.be/ Chemin des Chevreuils 1, B4000 Liège [email protected] Fracture Mechanics – NLFM – J-Integral Linear Elastic Fracture Mechanics (LEFM) y • Cracked body: summary s – 3 failure modes ∞ Mode I Mode II Mode III s s (opening) (sliding) (shearing) yy yy 2a x s∞ – Asymptotic solution governed by stress intensity factors syy 퐾 Asymptotic s 흈mode 푖 = 푖 푓mode 푖 휃 + ℴ 푟0 Zone of asymptotic yy 2휋r solution (in terms of 1/r1/2) dominance True syy mode 푖 푟 mode 푖 0 풖 = 퐾푖 푔 휃 + ℴ 푟 2휋 x Plasticity Structural response 2021-2022 Fracture Mechanics – NLFM – J-Integral 2 Linear Elastic Fracture Mechanics (LEFM) • Cracked body: summary – Potential energy PT = Eint - Qu before – Crack closure integral • Energy required to close crack tip 풖+횫풖 ′ ′ ΔΠ푇 = 풕 ⋅ 풖 푑풖 푑퐴 Da Δ퐴 풖 after – Energy release rate ti 0 • Variation of potential energy in case of crack growth t i 퐺 = −휕A 퐸int − 푊ext = −휕퐴ΔΠ푇 • In linear elasticity 0 . 1 1 ퟎ t Du/2 퐺 = −휕퐴ΔΠ푇 = − lim 풕 ⋅ 횫풖 푑퐴 Δ퐴→0 Δ퐴 Δ퐴 2 0 u0 u0 +Du u – In linear elasticity & if crack grows straight ahead i i i i 퐾2 퐾2 퐾2 퐺 = 퐼 + 퐼퐼 + 퐼퐼퐼 퐸′ 퐸′ 2휇 2021-2022 Fracture Mechanics – NLFM – J-Integral 3 Linear Elastic Fracture Mechanics (LEFM) • Cracked body: summary B – J-integral y r D q • Strain energy flow x a G – Exists if an internal potential exists • Is path independent if the contour G embeds a straight crack tip • No assumption on subsequent growth direction • Can be extended to plasticity if no unloading (see later) – If crack grows straight ahead G=J – In linear elasticity (independently of crack growth direction): 2021-2022 Fracture Mechanics – NLFM – J-Integral 4 Linear Elastic Fracture Mechanics (LEFM) • Analytical y y y – SIF from full-field solution s∞ • Limited cases t∞ t∞ s x x s∞ x ∞ 2a 2a 2a t∞ t∞ s∞ – From energetic consideration 2 2 2 퐾퐼 퐾퐼퐼 퐾퐼퐼퐼 • Growing straight ahead crack 퐺 = −휕 퐸 − 푊 퐺 = + + A int ext 퐸′ 퐸′ 2휇 • From J-integral • Numerical (e.g. FEM) – bi depends on geometry & crack length • Tabulated solutions (handbooks) – http://ebooks.asmedigitalcollection.asme.org/book.aspx?bookid=230 2021-2022 Fracture Mechanics – NLFM – J-Integral 5 Linear Elastic Fracture Mechanics (LEFM) • Small Scale Yielding assumption – LEFM: we have assumed the existence of a K-dominance zone syy Does not always syy K-dominance zone Asymptotic syy exist LEFM asymptotic ( asymptotic -1/2 syy in r solution in 1/r1/2) True syy True syy x x Plasticity • This holds of if the process zone (in which irreversible process occurs) – Is a small region compared to the specimen size & – Is localized at the crack tip – Validity of this approach? • We check the dimensions ∝Process 2 퐾퐼 zone size 푎, 푊 − 푎 > 2.5 0 휎푝 • Non-linear fracture mechanics – Derivation of the LEFM validity criterion – Providing solutions when LEFM criterion is not met 2021-2022 Fracture Mechanics – NLFM – J-Integral 6 Elastoplastic behavior • Power law – This law can be rewritten in terms of the total deformations • Yield stress is replaced by 2 equivalent stress 1.5 • Plastic strain is replaced by p 0 0 p s s / 1 equivalent strain / = 2; n = 1 s s = 4; n = 1 = 2; n = 4 • The governing law becomes 0.5 = 4; n = 4 = 2; n = 11 = 4; n = 11 or 0 0 2 4 6 8 10 0 E/s 0 • Parameter n E / sp p – n→∞: perfect plasticity – n→1: “elasticity” – Doing so requires 2 assumptions • There is no unloading • As elastic strains are assimilated to plastic strains, the material is incompressible – Which are satisfied if • We are interested only in crack initiation and not in crack propagation • The stress components remain proportional with the loading • Elastic deformations are negligible compared to plastic ones 2021-2022 Fracture Mechanics – NLFM – J-Integral 7 HRR field • Summary 2.5 s~ ; n = 3 rr – Assumptions Plane ~s ; n = 3 2 qq ~s ; n = 3 • J2-plasticity with power law description rq ~s ; n = 3 • Small deformations 1.5 e ~ s • There is no unloading and loading is 1 proportional in all the directions (ok for crack initiation and not for crack propagation) 0.5 • Elastic strains are assimilated to plastic strain 0 0 50 100 150 (material is incompressible) q [degq [°].] • Semi-infinite crack 7 – HRR results for semi-infinite mode I crack Plane • Asymptotic stress, strain and displacement fields 6 Plane s 5 4 n I 3 2 1 0 0 5 10 15 n n • J is a “plastic strain intensity factor” 2021-2022 Fracture Mechanics – NLFM – J-Integral 8 HRR field • Summary (2) 0.2 n = 3; Plane – HRR results for semi-infinite mode I crack (2) n = 3; Plane s • Process zone 0.1 y ~ 0 with -0.1 – If SSY • CTOD -0.2 – New definition -0.2 -0.1 0 0.1 0.2 ~x y 1 s0/E = 0.001 p ux Plane s0/E = 0.002 u 0.8 p y s0/E = 0.004 p s0/E = 0.008 x 0.6 p r* n d 0.4 – 0.2 – Also function of J 0 0 0.1 0.2 0.3 0.4 0.5 – We did not assume SSY !!! 1/n 2021-2022 Fracture Mechanics – NLFM – J-Integral 9 HRR field • Validity in SSY – We have two asymptotic solutions • HRR field is valid in the process zone • LEFM is still valid in the elastic zone close to the crack tip HRR asymptotic HRR asymptotic yy -1/(n+1) s s in r -1/(n+1) yy syy in r syy n+1 LEFM asymptotic Log 1 s in r-1/2 yy 2 True syy LEFM 1 asymptotic x -1/2 Plasticity syy in r Log r – Conditions • This is the case if all sizes are 25 times larger than the plastic zone t a L 2021-2022 Fracture Mechanics – NLFM – J-Integral 10 HRR field • Validity in elasto-plastic conditions – Deformations are small – We still have one asymptotic solution valid • HRR field is valid in the process zone – LEFM is NOT valid in the elastic zone close to the crack HRR asymptotic yy -1/(n+1) HRR asymptotic s syy in r s in r-1/(n+1) n+1 yy Log syy 1 LEFM asymptotic -1/2 syy in r 2 True syy LEFM 1 asymptotic -1/2 x syy in r Plasticity Log r – Conditions • This is the case if all sizes are 25 times larger than CTOD t a L 2021-2022 Fracture Mechanics – NLFM – J-Integral 11 HRR field • Validity in large yielding – Example: ligament size is too small – Small deformations assumption does not hold – Neither HRR field nor LEFM asymptotic fields are valid HRR asymptotic HRR asymptotic yy -1/(n+1) -1/(n+1) s s in r syy in r yy syy n+1 LEFM asymptotic Log 1 -1/2 syy in r True syy 2 LEFM 1 x asymptotic -1/2 Plasticity syy in r Log r – There is no zone of J-dominance – Plastic strain concentrations depend on the experiment 2021-2022 Fracture Mechanics – NLFM – J-Integral 12 HRR field • Crack initiation criteria – In SSY: • Criteria based on J or dt are valid: J ≥ JC or dt ≥ dC – J & dt depend on a, the geometry, the loading, … • But as the LEFM solution holds, we can still use K(a)≥KC 0 – May be corrected by using the effective length aeff if s∞< 50% of sp – In Elasto-Plastic conditions: • Criteria based on J or dt are valid: J ≥ JC or dt ≥ dC – J & dt depend on a, the geometry, the loading, … • The LEFM solution DOES NOT hold, we CANNOT use K(a)≥KC – In Large Scale Yielding • Plastic strain concentrations depend on the experiment • Zones near free boundaries or other cracks tend to be less stressed – Solution is no longer uniquely governed by J – Relation between J & dt is dependent on the configuration and on the loading – The critical JC measured for an experiment might not be valid for another one – A 2-parameter characterization is needed 2021-2022 Fracture Mechanics – NLFM – J-Integral 13 Relation J-G • For elasto-plastic materials – J is a useful concept as it can be used as crack initiation criterion – Relation J-G • J = G if an internal potential is defined & if the crack grows straight ahead • For an elasto-plastic material – Since no internal potential can be defined J ≠ G – But let us consider two specimens 1: Non-linear 2: Elasto- » One with a non-linear elastic material (1) elasticity plasticity » One with an elasto-plastic material (2) with the same loading response J1=G1 J ? G – If the crack will grow straight ahead 2 2 s » J1 = G1 as there is a potential defined Q Q » Before crack propagation (which True would involve possible unloading) sTS the stress state is the same for the two materials J2 = J1 = G1 = G2 • If the crack will grow straight ahead, before crack propagation: J = G for an elasto-plastic material E p e True 2021-2022 Fracture Mechanics – NLFM – J-Integral 14 Computation of J • Available methods of computing J – Numerical (see previous lectures) • Contour integral • Domain integral – Energetic approach • Numerical • Experimental – Experimental • Multiple specimen testing • Deeply notched SENB • Eta factor approach – Engineering • Use of handbooks • If J expression is known it can be applied to – Fracture toughness test – Fracture criteria and stability prediction 2021-2022 Fracture Mechanics – NLFM – J-Integral 15 Computation of J : Energetic approach • Prescribed displacement – Let us consider a specimen • With a prescribed displacement • A compliance depending on the crack length – Using compliance curves • Energy release rate: Q Q+dQ • Internal energy: • Energy release rate in terms of displacements – We have Q’ Q’ A A Q Q’ du A’ > A Eint E int u' u' u u 2021-2022 Fracture Mechanics – NLFM – J-Integral 16 Computation of J : Energetic approach Q • Prescribed displacement (2) Q* – Interpretation of Loading Crack A=A Q*+dQ 0 growth for an elastic material • Body with crack surface A0 loaded up to Q* Unloading • Crack growth dA at constant grip A=A0+dA the specimen becomes more flexible u u* the load decreases by •
Load more

Recommended publications
  • 10-1 CHAPTER 10 DEFORMATION 10.1 Stress-Strain Diagrams And
    EN380 Naval Materials Science and Engineering Course Notes, U.S. Naval Academy CHAPTER 10 DEFORMATION 10.1 Stress-Strain Diagrams and Material Behavior 10.2 Material Characteristics 10.3 Elastic-Plastic Response of Metals 10.4 True stress and strain measures 10.5 Yielding of a Ductile Metal under a General Stress State - Mises Yield Condition. 10.6 Maximum shear stress condition 10.7 Creep Consider the bar in figure 1 subjected to a simple tension loading F. Figure 1: Bar in Tension Engineering Stress () is the quotient of load (F) and area (A). The units of stress are normally pounds per square inch (psi). = F A where: is the stress (psi) F is the force that is loading the object (lb) A is the cross sectional area of the object (in2) When stress is applied to a material, the material will deform. Elongation is defined as the difference between loaded and unloaded length ∆푙 = L - Lo where: ∆푙 is the elongation (ft) L is the loaded length of the cable (ft) Lo is the unloaded (original) length of the cable (ft) 10-1 EN380 Naval Materials Science and Engineering Course Notes, U.S. Naval Academy Strain is the concept used to compare the elongation of a material to its original, undeformed length. Strain () is the quotient of elongation (e) and original length (L0). Engineering Strain has no units but is often given the units of in/in or ft/ft. ∆푙 휀 = 퐿 where: is the strain in the cable (ft/ft) ∆푙 is the elongation (ft) Lo is the unloaded (original) length of the cable (ft) Example Find the strain in a 75 foot cable experiencing an elongation of one inch.
    [Show full text]
  • Mechanics of Materials Plasticity
    Provided for non-commercial research and educational use. Not for reproduction, distribution or commercial use. This article was originally published in the Reference Module in Materials Science and Materials Engineering, published by Elsevier, and the attached copy is provided by Elsevier for the author’s benefit and for the benefit of the author’s institution, for non-commercial research and educational use including without limitation use in instruction at your institution, sending it to specific colleagues who you know, and providing a copy to your institution’s administrator. All other uses, reproduction and distribution, including without limitation commercial reprints, selling or licensing copies or access, or posting on open internet sites, your personal or institution’s website or repository, are prohibited. For exceptions, permission may be sought for such use through Elsevier’s permissions site at: http://www.elsevier.com/locate/permissionusematerial Lubarda V.A., Mechanics of Materials: Plasticity. In: Saleem Hashmi (editor-in-chief), Reference Module in Materials Science and Materials Engineering. Oxford: Elsevier; 2016. pp. 1-24. ISBN: 978-0-12-803581-8 Copyright © 2016 Elsevier Inc. unless otherwise stated. All rights reserved. Author's personal copy Mechanics of Materials: Plasticity$ VA Lubarda, University of California, San Diego, CA, USA r 2016 Elsevier Inc. All rights reserved. 1 Yield Surface 1 1.1 Yield Surface in Strain Space 2 1.2 Yield Surface in Stress Space 2 2 Plasticity Postulates, Normality and Convexity
    [Show full text]
  • Identification of Rock Mass Properties in Elasto-Plasticity D
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Archive Ouverte en Sciences de l'Information et de la Communication Identification of rock mass properties in elasto-plasticity D. Deng, D. Nguyen Minh To cite this version: D. Deng, D. Nguyen Minh. Identification of rock mass properties in elasto-plasticity. Computers and Geotechnics, Elsevier, 2003, 30, pp.27-40. 10.1016/S0266-352X(02)00033-2. hal-00111371 HAL Id: hal-00111371 https://hal.archives-ouvertes.fr/hal-00111371 Submitted on 26 Sep 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Identification of rock mass properties in elasto-plasticity Desheng Deng*, Duc Nguyen-Minh Laboratoire de Me´canique des Solides, E´cole Polytechnique, 91128 Palaiseau, France Abstract A simple and effective back analysis method has been proposed on the basis of a new cri-terion of identification, the minimization of error on the virtual work principle. This method works for both linear elastic and nonlinear elasto-plastic problems. The elasto-plastic rock mass properties for different criteria of plasticity can be well identified based on field measurements.
    [Show full text]
  • Crystal Plasticity Model with Back Stress Evolution. Wei Huang Louisiana State University and Agricultural & Mechanical College
    Louisiana State University LSU Digital Commons LSU Historical Dissertations and Theses Graduate School 1996 Crystal Plasticity Model With Back Stress Evolution. Wei Huang Louisiana State University and Agricultural & Mechanical College Follow this and additional works at: https://digitalcommons.lsu.edu/gradschool_disstheses Recommended Citation Huang, Wei, "Crystal Plasticity Model With Back Stress Evolution." (1996). LSU Historical Dissertations and Theses. 6154. https://digitalcommons.lsu.edu/gradschool_disstheses/6154 This Dissertation is brought to you for free and open access by the Graduate School at LSU Digital Commons. It has been accepted for inclusion in LSU Historical Dissertations and Theses by an authorized administrator of LSU Digital Commons. For more information, please contact [email protected]. INFORMATION TO USERS This manuscript has been reproduced from the microfilm master. UMI films the text directly from the original or copy submitted. Thus, some thesis and dissertation copies are in typewriter face, while others may be from any type o f computer printer. The quality of this reproduction is dependent upon the quality of the copy submitted. Broken or indistinct print, colored or poor quality illustrations and photographs, print bleedthrough, substandard margins, and improper alignment can adversely affect reproduction. In the unlikely event that the author did not send UMI a complete manuscript and there are missing pages, these will be noted. Also, if unauthorized copyright material had to be removed, a note will indicate the deletion. Oversize materials (e.g., maps, drawings, charts) are reproduced by sectioning the original, beginning at the upper left-hand comer and continuing from left to right in equal sections with small overlaps.
    [Show full text]
  • Crack Tip Elements and the J Integral
    EN234: Computational methods in Structural and Solid Mechanics Homework 3: Crack tip elements and the J-integral Due Wed Oct 7, 2015 School of Engineering Brown University The purpose of this homework is to help understand how to handle element interpolation functions and integration schemes in more detail, as well as to explore some applications of FEA to fracture mechanics. In this homework you will solve a simple linear elastic fracture mechanics problem. You might find it helpful to review some of the basic ideas and terminology associated with linear elastic fracture mechanics here (in particular, recall the definitions of stress intensity factor and the nature of crack-tip fields in elastic solids). Also check the relations between energy release rate and stress intensities, and the background on the J integral here. 1. One of the challenges in using finite elements to solve a problem with cracks is that the stress field at a crack tip is singular. Standard finite element interpolation functions are designed so that stresses remain finite a everywhere in the element. Various types of special b c ‘crack tip’ elements have been designed that 3L/4 incorporate the singularity. One way to produce a L/4 singularity (the method used in ABAQUS) is to mesh L the region just near the crack tip with 8 noded elements, with a special arrangement of nodal points: (i) Three of the nodes (nodes 1,4 and 8 in the figure) are connected together, and (ii) the mid-side nodes 2 and 7 are moved to the quarter-point location on the element side.
    [Show full text]
  • Tuning the Performance of Metallic Auxetic Metamaterials by Using Buckling and Plasticity
    materials Article Tuning the Performance of Metallic Auxetic Metamaterials by Using Buckling and Plasticity Arash Ghaedizadeh 1, Jianhu Shen 1, Xin Ren 1,2 and Yi Min Xie 1,* Received: 28 November 2015; Accepted: 8 January 2016; Published: 18 January 2016 Academic Editor: Geminiano Mancusi 1 Centre for Innovative Structures and Materials, School of Engineering, RMIT University, GPO Box 2476, Melbourne 3001, Australia; [email protected] (A.G.); [email protected] (J.S.); [email protected] (X.R.) 2 Key Laboratory of Traffic Safety on Track, School of Traffic & Transportation Engineering, Central South University, Changsha 410075, China * Correspondence: [email protected]; Tel.: +61-3-9925-3655 Abstract: Metallic auxetic metamaterials are of great potential to be used in many applications because of their superior mechanical performance to elastomer-based auxetic materials. Due to the limited knowledge on this new type of materials under large plastic deformation, the implementation of such materials in practical applications remains elusive. In contrast to the elastomer-based metamaterials, metallic ones possess new features as a result of the nonlinear deformation of their metallic microstructures under large deformation. The loss of auxetic behavior in metallic metamaterials led us to carry out a numerical and experimental study to investigate the mechanism of the observed phenomenon. A general approach was proposed to tune the performance of auxetic metallic metamaterials undergoing large plastic deformation using buckling behavior and the plasticity of base material. Both experiments and finite element simulations were used to verify the effectiveness of the developed approach. By employing this approach, a 2D auxetic metamaterial was derived from a regular square lattice.
    [Show full text]
  • On the Path-Dependence of the J-Integral Near a Stationary Crack in an Elastic-Plastic Material
    On the Path-Dependence of the J-integral Near a Stationary Crack in an Elastic-Plastic Material Dorinamaria Carka and Chad M. Landis∗ The University of Texas at Austin, Department of Aerospace Engineering and Engineering Mechanics, 210 East 24th Street, C0600, Austin, TX 78712-0235 Abstract The path-dependence of the J-integral is investigated numerically, via the finite element method, for a range of loadings, Poisson's ratios, and hardening exponents within the context of J2-flow plasticity. Small-scale yielding assumptions are employed using Dirichlet-to-Neumann map boundary conditions on a circular boundary that encloses the plastic zone. This construct allows for a dense finite element mesh within the plastic zone and accurate far-field boundary conditions. Details of the crack tip field that have been computed previously by others, including the existence of an elastic sector in Mode I loading, are confirmed. The somewhat unexpected result is that J for a contour approaching zero radius around the crack tip is approximately 18% lower than the far-field value for Mode I loading for Poisson’s ratios characteristic of metals. In contrast, practically no path-dependence is found for Mode II. The applications of T or S stresses, whether applied proportionally with the K-field or prior to K, have only a modest effect on the path-dependence. Keywords: elasto-plastic fracture mechanics, small scale yielding, path-dependence of the J-integral, finite element methods 1. Introduction The J-integral as introduced by Eshelby [1,2] and Rice [3] is perhaps the most useful quantity for the analysis of the mechanical fields near crack tips in both linear elastic and non-linear elastic materials.
    [Show full text]
  • Introduction to FINITE STRAIN THEORY for CONTINUUM ELASTO
    RED BOX RULES ARE FOR PROOF STAGE ONLY. DELETE BEFORE FINAL PRINTING. WILEY SERIES IN COMPUTATIONAL MECHANICS HASHIGUCHI WILEY SERIES IN COMPUTATIONAL MECHANICS YAMAKAWA Introduction to for to Introduction FINITE STRAIN THEORY for CONTINUUM ELASTO-PLASTICITY CONTINUUM ELASTO-PLASTICITY KOICHI HASHIGUCHI, Kyushu University, Japan Introduction to YUKI YAMAKAWA, Tohoku University, Japan Elasto-plastic deformation is frequently observed in machines and structures, hence its prediction is an important consideration at the design stage. Elasto-plasticity theories will FINITE STRAIN THEORY be increasingly required in the future in response to the development of new and improved industrial technologies. Although various books for elasto-plasticity have been published to date, they focus on infi nitesimal elasto-plastic deformation theory. However, modern computational THEORY STRAIN FINITE for CONTINUUM techniques employ an advanced approach to solve problems in this fi eld and much research has taken place in recent years into fi nite strain elasto-plasticity. This book describes this approach and aims to improve mechanical design techniques in mechanical, civil, structural and aeronautical engineering through the accurate analysis of fi nite elasto-plastic deformation. ELASTO-PLASTICITY Introduction to Finite Strain Theory for Continuum Elasto-Plasticity presents introductory explanations that can be easily understood by readers with only a basic knowledge of elasto-plasticity, showing physical backgrounds of concepts in detail and derivation processes
    [Show full text]
  • Cross-Linked Polymers and Rubber Elasticity Chapter 9 (Sperling)
    Cross-linked Polymers and Rubber Elasticity Chapter 9 (Sperling) • Definition of Rubber Elasticity and Requirements • Cross-links, Networks, Classes of Elastomers (sections 1-3, 16) • Simple Theory of Rubber Elasticity (sections 4-8) – Entropic Origin of Elastic Retractive Forces – The Ideal Rubber Behavior • Departures from the Ideal Rubber Behavior (sections 9-11) – Non-zero Energy Contribution to the Elastic Retractive Forces – Stress-induced Crystallization and Limited Extensibility of Chains (How to make better elastomers: High Strength and High Modulus) – Network Defects (dangling chains, loops, trapped entanglements, etc..) – Semi-empirical Mooney-Rivlin Treatment (Affine vs Non-Affine Deformation) Definition of Rubber Elasticity and Requirements • Definition of Rubber Elasticity: Very large deformability with complete recoverability. • Molecular Requirements: – Material must consist of polymer chains. Need to change conformation and extension under stress. – Polymer chains must be highly flexible. Need to access conformational changes (not w/ glassy, crystalline, stiff mat.) – Polymer chains must be joined in a network structure. Need to avoid irreversible chain slippage (permanent strain). One out of 100 monomers must connect two different chains. Connections (covalent bond, crystallite, glassy domain in block copolymer) Cross-links, Networks and Classes of Elastomers • Chemical Cross-linking Process: Sol-Gel or Percolation Transition • Gel Characteristics: – Infinite Viscosity – Non-zero Modulus – One giant Molecule – Solid
    [Show full text]
  • Chapter 10: Elasticity and Oscillations
    Chapter 10 Lecture Outline 1 Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Chapter 10: Elasticity and Oscillations •Elastic Deformations •Hooke’s Law •Stress and Strain •Shear Deformations •Volume Deformations •Simple Harmonic Motion •The Pendulum •Damped Oscillations, Forced Oscillations, and Resonance 2 §10.1 Elastic Deformation of Solids A deformation is the change in size or shape of an object. An elastic object is one that returns to its original size and shape after contact forces have been removed. If the forces acting on the object are too large, the object can be permanently distorted. 3 §10.2 Hooke’s Law F F Apply a force to both ends of a long wire. These forces will stretch the wire from length L to L+L. 4 Define: L The fractional strain L change in length F Force per unit cross- stress A sectional area 5 Hooke’s Law (Fx) can be written in terms of stress and strain (stress strain). F L Y A L YA The spring constant k is now k L Y is called Young’s modulus and is a measure of an object’s stiffness. Hooke’s Law holds for an object to a point called the proportional limit. 6 Example (text problem 10.1): A steel beam is placed vertically in the basement of a building to keep the floor above from sagging. The load on the beam is 5.8104 N and the length of the beam is 2.5 m, and the cross-sectional area of the beam is 7.5103 m2.
    [Show full text]
  • Elastic Plastic Fracture Mechanics Elastic Plastic Fracture Mechanics Presented by Calvin M
    Fracture Mechanics Elastic Plastic Fracture Mechanics Elastic Plastic Fracture Mechanics Presented by Calvin M. Stewart, PhD MECH 5390-6390 Fall 2020 Outline • Introduction to Non-Linear Materials • J-Integral • Energy Approach • As a Contour Integral • HRR-Fields • COD • J Dominance Introduction to Non-Linear Materials Introduction to Non-Linear Materials • Thus far we have restricted our fractured solids to nominally elastic behavior. • However, structural materials often cannot be characterized via LEFM. Non-Linear Behavior of Materials • Two other material responses are that the engineer may encounter are Non-Linear Elastic and Elastic-Plastic Introduction to Non-Linear Materials • Loading Behavior of the two materials is identical but the unloading path for the elastic plastic material allows for non-unique stress- strain solutions. For Elastic-Plastic materials, a generic “Constitutive Model” specifies the relationship between stress and strain as follows n tot =+ Ramberg-Osgood 0 0 0 0 Reference (or Flow/Yield) Stress (MPa) Dimensionaless Constant (unitless) 0 Reference (or Flow/Yield) Strain (unitless) n Strain Hardening Exponent (unitless) Introduction to Non-Linear Materials • Ramberg-Osgood Constitutive Model n increasing Ramberg-Osgood −n K = 00 Strain Hardening Coefficient, K = 0 0 E n tot K,,,,0 n=+ E Usually available for a variety of materials 0 0 0 Introduction to Non-Linear Materials • Within the context of EPFM two general ways of trying to solve fracture problems can be identified: 1. A search for characterizing parameters (cf. K, G, R in LEFM). 2. Attempts to describe the elastic-plastic deformation field in detail, in order to find a criterion for local failure.
    [Show full text]
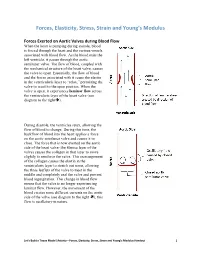
  • Forces, Elasticity, Stress, Strain and Young's Modulus Handout
    Forces, Elasticity, Stress, Strain and Young’s Modulus Forces Exerted on Aortic Valves during Blood Flow When the heart is pumping during systole, blood is forced through the heart and the various vessels associated with blood flow. As the blood exits the left ventricle, it passes through the aortic semilunar valve. The flow of blood, coupled with the mechanical structure of the heart valve, causes the valve to open. Essentially, the flow of blood and the forces associated with it cause the elastin in the ventricularis layer to “relax,” permitting the valve to recoil to the open position. When the valve is open, it experiences laminar flow across the ventricularis layer of the heart valve (see diagram to the right). During diastole, the ventricles relax, allowing the flow of blood to change. During this time, the backflow of blood into the heart applies a force on the aortic semilunar valve and causes it to close. The force that is now exerted on the aortic side of the heart valve (the fibrosa layer of the valve) causes the collagen in that layer to move slightly to reinforce the valve. This rearrangement of the collagen causes the elastin in the ventricularis layer to stretch out some, allowing the three leaflets of the valve to meet in the middle and completely seal the valve and prevent blood regurgitation. This change in blood flow means that the valve is no longer experiencing laminar flow. However, the movement of the blood creates some different currents on the aortic side of the valve (see diagram to the right ); this flow is oscillatory in nature.
    [Show full text]