DOCSLIB.ORG

Differential Geometry

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Differential Geometry Spring 2014 CSCI 599: Digital Geometry Processing 3.1 Classic Differential Geometry Hao Li http://cs599.hao-li.com !1 Spring 2014 CSCI 599: Digital Geometry Processing 3.1 Classic Differential Geometry With a Twist! Hao Li http://cs599.hao-li.com !2 Administrative • Exercise handouts: 11:59 PM every 2nd Wednesday • My first office hours later from 2pm to 4pm • This week only lecture. !3 Some Updates: run.usc.edu/vega Another awesome free library with half-edge data-structure By Prof. Jernej Barbic !4 FYI MeshLab! Popular Mesh Processing Software (meshlab.sourceforge.net) !5 FYI BeNTO3D! Mesh Processing Framework for Mac (www.bento3d.com) !6 Last Time Discrete Representations! • Explicit (parametric, polygonal meshes) Geometry • Implicit Surfaces (SDF, grid representation) Topology • Conversions • E→I: Closest Point, SDF, Fast Marching • I→E: Marching Cubes Algorithm !7 Differential Geometry Why do we care?! • Geometry of surfaces • Mothertongue of physical theories • Computation: processing / simulation !8 Motivation We need differential geometry to compute! • surface curvature • paramaterization distortion • deformation energies !9 Applications: 3D Reconstruction !10 Applications: Head Modeling !11 Applications: Facial Animation !12 Motivation Geometry is the key! • studied for centuries (Cartan, Poincaré, Lie, Hodge, de Rham, Gauss, Noether…) • mostly differential geometry • differential and integral calculus • invariants and symmetries !13 Getting Started How to apply DiffGeo ideas?! • surfaces as a collecition of samples • and topology (connectivity) • apply continuous ideas • BUT: setting is discrete • what is the right way? • discrete vs. discretized Let’s look at that first !14 Getting Started What characterizes structure(s)?! • What is shape? • Euclidean Invariance • What is physics? • Conservation/Balance Laws • What can we measure? • area, curvature, mass, flux, circulation !15 Getting Started Invariant descriptors! • quantities invariant under a set of transformations Intrinsic descriptor! • quantities which do notd depend on a coordinate frame !16 Outline • Parametric Curves • Parametric Surfaces Formalism & Intuition !17 Differential Geometry Leonard Euler (1707-1783) Carl Friedrich Gauss (1777-1855) !18 Parametric Curves x :[a, b] IR IR 3 ⊂ ⇥ x(b) x(t) a t b xt(t) x(a) x(t) dx(t) /dt dx(t) x(t)= y(t) x (t) := = dy(t) /dt t dt z(t) ⇥ dz(t) /dt ⇥ ⇤ ⌅ ⇤ ⌅ !19 Recall: Mappings Injective Surjective Bijective NO SELF-INTERSECTIONS! SELF-INTERSECTIONS! AMBIGUOUS PARAMETERIZATION !20 Parametric Curves A parametric curve x ( t ) is! • simple: x ( t ) is injective (no self-intersections) • differentiable: x ( t ) is defined for all t [a, b] t 2 • regular: x ( t ) =0 for all t [a, b] t 6 2 x(b) x(t) xt(t) x(a) !21 Length of a Curve Let t i = a + i ∆ t and xi = x(ti) xi x(a) x(b) a ∆t ti b !22 Length of a Curve Polyline chord length ∆x S = ∆x = i ∆t, ∆x := x x ⇥ i⇥ ∆t i ⇥ i+1 − i⇥ i i norm change ⇥ ⇥ Curve arc length ( ∆ t 0 ) x ! i t s = s(t)= xt dt a x(a) x(b) length = ! integration of infinitesimal change ! a ∆t ti b " norm of speed !23 Re-Parameterization Mapping of parameter domain u :[a, b] [c, d] → Re-parameterization w.r.t. u(t) [c, d] IR 3 ,t x(u(t)) → ⇥ Derivative (chain rule) dx(u(t)) dx du = = x (u(t)) u (t) dt du dt u t !24 Re-Parameterization Example 1 f : 0, IR 2 ,t (4t, 2t) 2 → ⇥ ⇥ 1 φ : 0, [0, 1] ,t 2t 2 → ⇥ ⇥ g : [0, 1] IR 2 ,t (2t, t) → ⇥ g(φ(t)) = f(t) ⇒ !25 Arc Length Parameterization Mapping of parameter domain: t t s(t)= x dt ⇥ ⇤ t⇤ a Parameter s for x ( s ) equals length from x ( a ) to x(s) x(s)=x(s(t)) ds = x dt t same infinitesimal change Special properties of resulting curve x (s) =1, x (s) x (s)=0 ⇥ s ⇥ s · ss defines orthonormal frame !26 The Frenet Frame Taylor expansion 1 1 x(t + h)=x(t)+x (t) h + x (t) h2 + x (t) h3 + ... t 2 tt 6 ttt for convergence analysis and approximations Define local frame ( t , n , b ) (Frenet frame) xt xt xtt t = n = b t b = × xt × xt xtt ⇥ × ⇥ tangent main normal binormal !27 The Frenet Frame Orthonormalization of local frame x ttt b xtt n xt t local affine frame Frenet frame !28 The Frenet Frame Frenet-Serret: Derivatives w.r.t. arc length s ts =+κn ns = κt +⇥b b = − ⇥n s − Curvature (deviation from straight line) b κ = x n ss t Torsion (deviation from planarity) 1 ⇥ = det([x , x , x ]) κ2 s ss sss !29 Curvature and Torsion Planes defined by x and two vectors:! • osculating plane: vectors t and n • normal plane: vectors n and b • rectifying plane: vectors t and b b n Osculating circle! • second order contact with curve t • center c = x +(1/)n • radius 1/ !30 Curvature and Torsion • Curvature: Deviation from straight line • Torsion: Deviation from planarity • Independent of parameterization • intrinsic properties of the curve • Euclidean invariants • invariant under rigid motion • Define curve uniquely up to a rigid motion !31 Curvature: Some Intuition A line through two points on the curve (Secant) !32 Curvature: Some Intuition A line through two points on the curve (Secant) !33 Curvature: Some Intuition Tangent, the first approximation limiting secant as the two points come together !34 Curvature: Some Intuition Circle of curvature Consider the circle passing through 3 pints of the curve !35 Curvature: Some Intuition Circle of curvature The limiting circle as three points come together !36 Curvature: Some Intuition Radius of curvature r !37 Curvature: Some Intuition Radius of curvature r !38 Curvature: Some Intuition Signed curvature Sense of traversal along curve !39 Curvature: Some Intuition Gauß map Point on curve maps to point on unit circle !40 Curvature: Some Intuition Shape operator (Weingarten map) Change in normal as we slide along curve negative directional derivative D of Gauß map describes directional curvature using normals as degrees of freedom! → accuracy/convergence/implementation (discretization) !41 Curvature: Some Intuition Turning number, k Number of orbits in Gaussian image !42 Curvature: Some Intuition Turning number theorem For a closed curve, the integral of curvature is an integer multiple of 2" !43 Take Home Message In the limit of a refinement sequence, discrete measure of length and curvature agree with continuous measures !44 Outline • Parametric Curves • Parametric Surfaces !45 Surfaces What characterizes shape?! • shape does not depend on Euclidean motions • metric and curvatures • smooth continuous notions to discrete notions !46 Metric on Surfaces Measure Stuff! • angle, length, area • requires an inner product • we have: • Euclidean inner product in domain • we want to turn this into: • inner product on surface !47 Parametric Surfaces Continuous surface x(u, v) x(u, v)= y(u, v) z(u, v) ⇥ n ⇤ ⌅ Normal vector xu xv p x x n = u × v x x ⇥ u × v⇥ Assume regular parameterization x x = 0 normal exists u × v ⇥ !48 Angles on Surface Curve [ u ( t ) ,v ( t )] in uv-plane defines curve on the surface x(u, v) c(t)=x(u(t) ,v(t)) Two curves c 1 and c 2 intersecting at!p • angle of intersection? n • two tangents t and t 1 2 xu xv p ! ti = αixu + ⇥ixv c2 • compute inner product c1 tT t = cos θ t t 1 2 1 2 !49 Angles on Surface Curve [ u ( t ) ,v ( t )] in uv-plane defines curve on the surface x(u, v) c(t)=x(u(t) ,v(t)) Two curves c 1 and c 2 intersecting at p T T t1 t2 =(α1xu + ⇥1xv) (α2xu + ⇥2xv) T T T = α1α2xu xu +(α1⇥2 + α2⇥1) xu xv + ⇥1⇥2xv xv T T xu xu xu xv α2 =(α1, ⇥1) T T xu xv xv xv ⇥2 ⇥ ⇥ !50 First Fundamental Form First fundamental form EF xT x xT x I = := u u u v FG xT x xT x ⇥ u v v v⇥ Defines inner product on tangent space T α α α α 1 , 2 := 1 I 2 ⇥ ⇥ ⇥ ⇥ ⇤ 1⇥ 2⇥⌅ 1⇥ 2⇥ !51 First Fundamental Form First fundamental form I allows to measure! (w.r.t. surface metric) Angles t>t = (↵ , β ), (↵ , β ) 1 2 h 1 1 2 2 i Length ds2 = (du, dv), (du, dv) squared ! ⇥ infinitesimal ! = Edu2 +2F dudv + Gdv2 length Area dA = x x du dv ⌅ u ⇤ v⌅ T T T 2 = x xu x xv (x xv) du dv infinitesimal ! u · v − u Area ⇥ = EG F 2du dv cross product →− determinant with unit vectors → area !52 Sphere Example Spherical parameterization cos u sin v x(u, v)= sin u sin v , (u, v) [0, 2π) [0, π) cos v ⇥ ⇥ × Tangent vectors⇤ ⌅ sin u sin v cos u cos v − x (u, v)= cos u sin v x (u, v)= sin u cos v u v ⇥ 0 ⇥ sin v − ⇤ ⌅ ⇤ ⌅ First fundamental Form sin2 v 0 I = 01 ⇥ !53 Sphere Example Length of equator x(t, ⇡/2) 2π 2π 2 2 1ds = E (ut) +2Futvt + G (vt) dt 0 0 ⇥ 2π = sin v dt 0 =2π sin v =2π !54 Sphere Example Area of a sphere π 2π π 2π 1dA = EG F 2 du dv 0 0 0 0 − ⇥ π 2π = sin v du dv 0 0 =4π !55 Normal Curvature Tangent vector t … n xu xv p t xu xv t = cos φ + sin φ ∥xu∥ ∥xv∥ unit vector !56 Normal Curvature … defines intersection plane, yielding curve c(t) normal curve n t c(t) p xu xv t = cos φ + sin φ ∥xu∥ ∥xv∥ !57 Geometry of the Normal Gauss map! • normal at point ! ! ! • consider curve in surface again • study its curvature at p • normal “tilts” along curve !58 Normal Curvature Normal curvature n ( t ) is defined as curvature of the normal curve c ( t ) at point p(t)=x(u, v) With second fundamental form ef xT nxT n II = := uu uv fg xT nxT n ⇥ ⇤ uv vv ⌅ normal curvature can be computed as T 2 2 ¯t II¯t ea +2fab + gb t = axu + bxv κ (¯t)= = n ¯tT I ¯t Ea2 +2F ab + Gb2 ¯t =(a, b) !59 Surface Curvature(s) Principal curvatures! • Maximum curvature κ1 = max κn(φ) φ • Minimum curvature κ2 = min κn(φ) φ 2 2 • Euler theorem κn(⇥)=κ1 cos ⇥ + κ2 sin ⇥ • Corresponding principal directions e 1 , e 2 are orthogonal !60 Surface Curvature(s) Principal curvatures! • Maximum curvature κ1 = max κn(φ) φ • Minimum curvature κ2 = min κn(φ) φ 2 2 • Euler theorem κn(⇥)=κ1
Load more

Recommended publications
  • J.M. Sullivan, TU Berlin A: Curves Diff Geom I, SS 2019 This Course Is an Introduction to the Geometry of Smooth Curves and Surf
    J.M. Sullivan, TU Berlin A: Curves Diff Geom I, SS 2019 This course is an introduction to the geometry of smooth if the velocity never vanishes). Then the speed is a (smooth) curves and surfaces in Euclidean space Rn (in particular for positive function of t. (The cusped curve β above is not regular n = 2; 3). The local shape of a curve or surface is described at t = 0; the other examples given are regular.) in terms of its curvatures. Many of the big theorems in the DE The lengthR [ : Länge] of a smooth curve α is defined as subject – such as the Gauss–Bonnet theorem, a highlight at the j j len(α) = I α˙(t) dt. (For a closed curve, of course, we should end of the semester – deal with integrals of curvature. Some integrate from 0 to T instead of over the whole real line.) For of these integrals are topological constants, unchanged under any subinterval [a; b] ⊂ I, we see that deformation of the original curve or surface. Z b Z b We will usually describe particular curves and surfaces jα˙(t)j dt ≥ α˙(t) dt = α(b) − α(a) : locally via parametrizations, rather than, say, as level sets. a a Whereas in algebraic geometry, the unit circle is typically be described as the level set x2 + y2 = 1, we might instead This simply means that the length of any curve is at least the parametrize it as (cos t; sin t). straight-line distance between its endpoints. Of course, by Euclidean space [DE: euklidischer Raum] The length of an arbitrary curve can be defined (following n we mean the vector space R 3 x = (x1;:::; xn), equipped Jordan) as its total variation: with with the standard inner product or scalar product [DE: P Xn Skalarproduktp ] ha; bi = a · b := aibi and its associated norm len(α):= TV(α):= sup α(ti) − α(ti−1) : jaj := ha; ai.
    [Show full text]
  • Geodetic Position Computations
    GEODETIC POSITION COMPUTATIONS E. J. KRAKIWSKY D. B. THOMSON February 1974 TECHNICALLECTURE NOTES REPORT NO.NO. 21739 PREFACE In order to make our extensive series of lecture notes more readily available, we have scanned the old master copies and produced electronic versions in Portable Document Format. The quality of the images varies depending on the quality of the originals. The images have not been converted to searchable text. GEODETIC POSITION COMPUTATIONS E.J. Krakiwsky D.B. Thomson Department of Geodesy and Geomatics Engineering University of New Brunswick P.O. Box 4400 Fredericton. N .B. Canada E3B5A3 February 197 4 Latest Reprinting December 1995 PREFACE The purpose of these notes is to give the theory and use of some methods of computing the geodetic positions of points on a reference ellipsoid and on the terrain. Justification for the first three sections o{ these lecture notes, which are concerned with the classical problem of "cCDputation of geodetic positions on the surface of an ellipsoid" is not easy to come by. It can onl.y be stated that the attempt has been to produce a self contained package , cont8.i.ning the complete development of same representative methods that exist in the literature. The last section is an introduction to three dimensional computation methods , and is offered as an alternative to the classical approach. Several problems, and their respective solutions, are presented. The approach t~en herein is to perform complete derivations, thus stqing awrq f'rcm the practice of giving a list of for11111lae to use in the solution of' a problem.
    [Show full text]
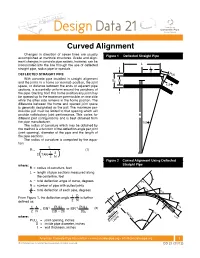
  • Design Data 21
    Design Data 21 Curved Alignment Changes in direction of sewer lines are usually Figure 1 Deflected Straight Pipe accomplished at manhole structures. Grade and align- Figure 1 Deflected Straight Pipe ment changes in concrete pipe sewers, however, can be incorporated into the line through the use of deflected L straight pipe, radius pipe or specials. t L 2 DEFLECTED STRAIGHT PIPE Pull With concrete pipe installed in straight alignment Bc D and the joints in a home (or normal) position, the joint ∆ space, or distance between the ends of adjacent pipe 1/2 N sections, is essentially uniform around the periphery of the pipe. Starting from this home position any joint may t be opened up to the maximum permissible on one side while the other side remains in the home position. The difference between the home and opened joint space is generally designated as the pull. The maximum per- missible pull must be limited to that opening which will provide satisfactory joint performance. This varies for R different joint configurations and is best obtained from the pipe manufacturer. ∆ 1/2 N The radius of curvature which may be obtained by this method is a function of the deflection angle per joint (joint opening), diameter of the pipe and the length of the pipe sections. The radius of curvature is computed by the equa- tion: L R = (1) 1 ∆ 2 TAN ( 2 N ) Figure 2 Curved Alignment Using Deflected Figure 2 Curved Alignment Using Deflected where: Straight Pipe R = radius of curvature, feet Straight Pipe L = length of pipe sections measured along the centerline, feet ∆ ∆ = total deflection angle of curve, degrees P.I.
    [Show full text]
  • Radius-Of-Curvature.Pdf
    CHAPTER 5 CURVATURE AND RADIUS OF CURVATURE 5.1 Introduction: Curvature is a numerical measure of bending of the curve. At a particular point on the curve , a tangent can be drawn. Let this line makes an angle Ψ with positive x- axis. Then curvature is defined as the magnitude of rate of change of Ψ with respect to the arc length s. Ψ Curvature at P = It is obvious that smaller circle bends more sharply than larger circle and thus smaller circle has a larger curvature. Radius of curvature is the reciprocal of curvature and it is denoted by ρ. 5.2 Radius of curvature of Cartesian curve: ρ = = (When tangent is parallel to x – axis) ρ = (When tangent is parallel to y – axis) Radius of curvature of parametric curve: ρ = , where and – Example 1 Find the radius of curvature at any pt of the cycloid , – Solution: Page | 1 – and Now ρ = = – = = =2 Example 2 Show that the radius of curvature at any point of the curve ( x = a cos3 , y = a sin3 ) is equal to three times the lenth of the perpendicular from the origin to the tangent. Solution : – – – = – 3a [–2 cos + ] 2 3 = 6 a cos sin – 3a cos = Now = – = Page | 2 = – – = – – = = 3a sin …….(1) The equation of the tangent at any point on the curve is 3 3 y – a sin = – tan (x – a cos ) x sin + y cos – a sin cos = 0 ……..(2) The length of the perpendicular from the origin to the tangent (2) is – p = = a sin cos ……..(3) Hence from (1) & (3), = 3p Example 3 If & ' are the radii of curvature at the extremities of two conjugate diameters of the ellipse = 1 prove that Solution: Parametric equation of the ellipse is x = a cos , y=b sin = – a sin , = b cos = – a cos , = – b sin The radius of curvature at any point of the ellipse is given by = = – – – – – Page | 3 = ……(1) For the radius of curvature at the extremity of other conjugate diameter is obtained by replacing by + in (1).
    [Show full text]
  • An Easier Derivation of the Curvature Formula from First Principles
    An easier derivation of the curvature formula from first principles Robert Ferguson Florida, USA bobferg13@comcast .net Introduction he radius of curvature formula is usually introduced in a university calculus Tcourse. Its proof is not included in most high school calculus courses and even some first-year university calculus courses because many students find the calculus used difficult (see Larson, Hostetler & Edwards, 2007, pp. 870– 872). Fortunately, there is an easier way to motivate and prove the radius of curvature formula without using formal calculus. An additional benefit is that the proof provides the coordinates of the centre of the corresponding circle of curvature. Understanding the proof requires only what advanced high school students already know: e.g., algebra, a little geometry about circles, and the intuition that both a circle and a curve have a slope and curvature. The proof is suitable for first-year university and advanced high school students. In terms of algebra, students need to know how to solve two simultaneous linear equations with two unknowns. In terms of geometry, students need to know that: 1. The radius of a circle drawn to a point of tangency between the circle and a tangent line is perpendicular to the tangent line. 2. If two separate lines are tangent to a circle at two different points, the lines drawn perpendicular to the tangent lines at their points of tangency intersect each other at the circle’s centre. 3. Each perpendicular line’s segment from its point of tangency to the point of intersection is a radius. The paper’s development of the radius of curvature formula can be used as an insightful application of the mathematics advanced high school students already know.
    [Show full text]
  • Differential Calculus—I
    UNIT I Differential Calculus—I 1.1 INTRODUCTION In many practical situations engineers and scientists come across problems which involve quantities of varying nature. Calculus in general, and differential calculus in particular, provide the analyst with several mathematical tools and techniques in studying how the functions involved in the problem behave. The student may recall at this stage that the derivative, obtained through the basic operation of calculus, called differentiation, measures the rate of change of the functions (dependent variable) with respect to the independent variable. In this chapter we examine how the concept of the derivative can be adopted in the study of curvedness or bending of curves. 1.2 RADIUS OF CURVATURE Let P be any point on the curve C. Draw the tangent at P to the Y C circle. The circle having the same curvature as the curve at P touching the curve at P, is called the circle of curvature. It is also O called the osculating circle. The centre of the circle of the cur- vature is called the centre of curvature. The radius of the circle P of curvature is called the radius of curvature and is denoted by ‘ρ’. Note : 1. If k (> 0) is the curvature of a curve at P, then the radius O X 1 of curvature of the curve of ρ is . This follows from the definition k Fig. 1.1 of radius of curvature and the result that the curvature of a circle is the reciprocal of its radius. dψ Note : 2. If for an arc of a curve, ψ decreases as s increases, then is negative, i.e., k is negative.
    [Show full text]
  • Differential Geometry Motivation
    (Discrete) Differential Geometry Motivation • Understand the structure of the surface – Properties: smoothness, “curviness”, important directions • How to modify the surface to change these properties • What properties are preserved for different modifications • The math behind the scenes for many geometry processing applications 2 Motivation • Smoothness ➡ Mesh smoothing • Curvature ➡ Adaptive simplification ➡ Parameterization 3 Motivation • Triangle shape ➡ Remeshing • Principal directions ➡ Quad remeshing 4 Differential Geometry • M.P. do Carmo: Differential Geometry of Curves and Surfaces, Prentice Hall, 1976 Leonard Euler (1707 - 1783) Carl Friedrich Gauss (1777 - 1855) 5 Parametric Curves “velocity” of particle on trajectory 6 Parametric Curves A Simple Example α1(t)() = (a cos(t), a s(sin(t)) t t ∈ [0,2π] a α2(t) = (a cos(2t), a sin(2t)) t ∈ [0,π] 7 Parametric Curves A Simple Example α'(t) α(t))( = (cos(t), s in (t)) t α'(t) = (-sin(t), cos(t)) α'(t) - direction of movement ⏐α'(t)⏐ - speed of movement 8 Parametric Curves A Simple Example α2'(t) α1'(t) α (t)() = (cos(t), sin (t)) t 1 α2(t) = (cos(2t), sin(2t)) Same direction, different speed 9 Length of a Curve • Let and 10 Length of a Curve • Chord length Euclidean norm 11 Length of a Curve • Chord length • Arc length 12 Examples y(t) x(t) • Straight line – x(t)=() = (t,t), t∈[0,∞) – x(t) = (2t,2t), t∈[0,∞) – x(t) = (t2,t2), t∈[0,∞) x(t) • Circle y(t) – x(t) = (cos(t),sin(t)), t∈[0,2π) x(t) x(t) 13 Examples α(t) = (a cos(t), a sin(t)), t ∈ [0,2π] α'(t) = (-a sin(t), a cos(t)) Many
    [Show full text]
  • Cubic Parabola in Railway Applications
    Cubic parabola in railway applications Cubic parabola is used in transition curves of the railway. The cubic parabola function is y=kx 3 (1) The “main” elements in railway transition curve are: The radius of curvature at the end of transition, the length L of the curve, the length l of its projection on x axis and the coefficient k. Two of these elements must be given in order for the curve to be defined, the other two can be calculated as described in this article. The 'secondary elements” of the curve are: the coordinates Rx and Ry of the center of curvature at the end of the transition, the shift f between the curve R and the x axis, the angle τ of the tangent to the curve at the end of the transition and and Yl, the y coordinate of the curve at length l. When the “main” elements are known, the “secondary” elements can easily be calculated. (Fig. 1). The radius of curvature r at a point of the curve y=f(x) is given by: 3 2 2 4 1+f© x 19k x r= r= . f©© x For the cubic parabola therefore: 6kx (2) Fig. 1. Elements of transition curve The centre of curvature in a point (x,y) of a curve y=f(x) has the following coordinates: 2 2 1+f© x 1+f© x x =x− f© x y =y+ c f©© x c f© x For the cubic parabola these coordinates are: x 1−9k 2 x4 15 k 2 x 41 x = y = (3) c 2 c 6kx The length s of a curve y=f(x) from 0 to x is: x x 2 s=∫ 1+f© x dx and for the cubic parabola: s=∫ 19k2 x4 dx (4) 0 0 The tangent to the parabola at a point x (which is perpendicular to the corresponding radius r) forms an angle φ with x-axis whose tangent is equal to the derivative at point x: tan φ= kx 3 © ή: tan φ=3kx2 (5).
    [Show full text]
  • The Frenet–Serret Formulas∗
    The Frenet–Serret formulas∗ Attila M´at´e Brooklyn College of the City University of New York January 19, 2017 Contents Contents 1 1 The Frenet–Serret frame of a space curve 1 2 The Frenet–Serret formulas 3 3 The first three derivatives of r 3 4 Examples and discussion 4 4.1 Thecurvatureofacircle ........................... ........ 4 4.2 Thecurvatureandthetorsionofahelix . ........... 5 1 The Frenet–Serret frame of a space curve We will consider smooth curves given by a parametric equation in a three-dimensional space. That is, writing bold-face letters of vectors in three dimension, a curve is described as r = F(t), where F′ is continuous in some interval I; here the prime indicates derivative. The length of such a curve between parameter values t I and t I can be described as 0 ∈ 1 ∈ t1 t1 ′ dr (1) σ(t1)= F (t) dt = dt Z | | Z dt t0 t0 where, for a vector u we denote by u its length; here we assume t is fixed and t is variable, so | | 0 1 we only indicated the dependence of the arc length on t1. Clearly, σ is an increasing continuous function, so it has an inverse σ−1; it is customary to write s = σ(t). The equation − def (2) r = F(σ 1(s)) s J = σ(t): t I ∈ { ∈ } is called the re-parametrization of the curve r = F(t) (t I) with respect to arc length. It is clear that J is an interval. To simplify the description, we will∈ always assume that r = F(t) and s = σ(t), ∗Written for the course Mathematics 2201 (Multivariable Calculus) at Brooklyn College of CUNY.
    [Show full text]
  • CURVILINEAR MOTION: NORMAL and TANGENTIAL COMPONENTS Today’S Objectives: Students Will Be Able To: 1
    CURVILINEAR MOTION: NORMAL AND TANGENTIAL COMPONENTS Today’s Objectives: Students will be able to: 1. Determine the normal and tangential components of In-Class Activities: velocity and acceleration of a • Check Homework particle traveling along a • Reading Quiz curved path. • Applications • Normal and Tangential Components of Velocity and Acceleration • Special Cases of Motion • Concept Quiz • Group Problem Solving • Attention Quiz READING QUIZ 1. If a particle moves along a curve with a constant speed, then its tangential component of acceleration is A) positive. B) negative. C) zero. D) constant. 2. The normal component of acceleration represents A) the time rate of change in the magnitude of the velocity. B) the time rate of change in the direction of the velocity. C) magnitude of the velocity. D) direction of the total acceleration. APPLICATIONS Cars traveling along a clover-leaf interchange experience an acceleration due to a change in speed as well as due to a change in direction of the velocity. If the car’s speed is increasing at a known rate as it travels along a curve, how can we determine the magnitude and direction of its total acceleration? Why would you care about the total acceleration of the car? APPLICATIONS (continued) A motorcycle travels up a hill for which the path can be approximated by a function y = f(x). If the motorcycle starts from rest and increases its speed at a constant rate, how can we determine its velocity and acceleration at the top of the hill? How would you analyze the motorcycle's “flight” at the top of the hill? NORMAL AND TANGENTIAL COMPONENTS (Section 12.7) When a particle moves along a curved path, it is sometimes convenient to describe its motion using coordinates other than Cartesian.
    [Show full text]
  • Radius of the Earth - Radii Used in Geodesy James R
    Radius of the Earth - Radii Used in Geodesy James R. Clynch Naval Postgraduate School, 2002 I. Three Radii of Earth and Their Use There are three radii that come into use in geodesy. These are a function of latitude in the ellipsoidal model of the earth. The physical radius, the distance from the center of the earth to the ellipsoid is the least used. The other two are the radii of curvature. If you wish to convert a small difference of latitude or longitude into the linear distance on the surface of the earth, then the spherical earth equation would be, dN = R df, dE = R cosf dl where R is the radius of the sphere and the angle differences are in radians. The values dN and dE are distances in the surface of the sphere. For an ellipsoidal earth there is a different radius for each of the directions. The radius used for the longitude is called the Radius of Curvature in the prime vertical. It is denoted by RN, N, or n , or a few other symbols. (Note that in these notes the symbol N is used for the geoid undulation.) It has a nice physical interpretation. At the latitude chosen go down the line perpendicular to the ellipsoid surface until you intersect the polar axis. This distance is RN. The radius used for the latitude change to North distance is called the Radius of Curvature in the meridian. It is denoted by RM, or M, or several other symbols. It has no good physical interpretation on a figure.
    [Show full text]
  • RADIUS of CURVATURE and EVOLUTE of the FUNCTION Y=F(X)
    RADIUS OF CURVATURE AND EVOLUTE OF THE FUNCTION y=f(x) In introductory calculus one learns about the curvature of a function y=f(x) and also about the path (evolute) that the center of curvature traces out as x is varied along the original curve. Beginning students sometimes have difficulty in deriving and understanding the quantity [1+(df/dx)2]3/2which enters such calculations. We want here to review these concepts and add a few simplifying thoughts which will help clarify the problem. We start with a continuous curve y=f(x) as shown – An increment of length ds along this curve is- df ds dx 2 dy 2 dx 1 ( )2 dx Also we have that at x the angle between the x axis and the curve is- dy arctan( ) arctan[ f '(x)] dx Differentiating this last expression with respect to x produces- f "(x) d dx [1 f '(x)2 ] If we now go back to the above figure, we see that at any point x along the curve y=f(x) there lies a unique circle whose radius represents the radius of curvature r=. Mathematically we have- ds dx 1 f '(x)2 [1 f '(x)2 ]3/ 2 | | d { f "(x)dx /[ 1 f '(x)2 ] f "(x) The absolute value symbol has been added because should always be considered a positive quantity. Notice this radius of curvature is just the reciprocal of standard curvature, usually, designated by K. The curvature of f(x) changes sign as one passes through an inflection point where f ”(x)=0.
    [Show full text]