DOCSLIB.ORG

Differential Geometry (And a Bit of Topology) Multi-Dimensional Derivatives Derivative of a Function

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Differential Geometry (And a Bit of Topology) Multi-Dimensional Derivatives Derivative of a Function Geometric Modeling Summer Semester 2012 Differential Geometry (and a bit of Topology) Multi-Dimensional Derivatives Derivative of a Function Reminder: The derivative of a function is defined as d f (t h) f (t) f (t): lim dt h0 h If limit exists: function is called differentiable. Other notation: d d k f (t) f '(t) f (t) f (t) f (k )(t) dt k variable time dt from context variables repeated differentiation (higher order derivatives) Taylor Approximation Smooth functions can be approximated locally: • f (x) f (x0 ) d f (x )x x dx 0 0 1 d 2 f (x )x x 2 ... 2 dx2 0 0 1 d k ... f (x )x x k O(x k1 ) k! dx k 0 0 • Convergence: holomorphic functions • Local approximation for smooth functions Rule of Thumb Derivatives and Polynomials 2 3 • Polynomial: 푓 푥 = 푐0 + 푐1푥 + 푐2푥 + 푐3푥 … . 0th-order derivative: 푓 0 = 푐0 . 1st-order derivative: 푓′ 0 = 푐1 . 2nd-order derivative: 푓′′ 0 = 2푐2 . 3rd-order derivative: 푓′′′ 0 = 6푐3 . ... Rule of Thumb: • Derivatives correspond to polynomial coefficients • Estimate derivatives polynomial fitting Partial Derivative Multivariate functions: • Notation changes: use curly-d f (x1 ,..., xk1 ,xk ,xk1 ,..., xn ): xk f (x ,..., x ,x h,x ,..., x ) f (x ,..., x ,x ,x ,..., x ) lim 1 k1 k k1 n 1 k1 k k1 n h0 h • Alternative notation: f (x) f (x) f (x) k xk xk Special Cases Derivatives for: • Functions f: n (“heightfield”) • Functions f: n (“curves”) • Functions f: n m (general case) Special Cases Derivatives for: f(x, y) • Functions f: n (“height field”) • Functions f: n (“curves”) x2 • Functions f: n m (general case) x1 height field Gradient Gradient: • Given a function f: n (“heightfield”) • The vector of all partial derivatives of f is called the gradient: f (x) x1 x1 f (x) f (x) f (x) x x n n Gradient Gradient: f(x0 )f(x0 )(x x0 ) f(x) f(x) f(x) x x 0 x1 x1 x2 x2 • gradient: vector pointing in direction of steepest ascent. • Local linear approximation (Taylor): f (x) f (x0 ) f (x0 )(x x0 ) Higher Order Derivatives Higher order Derivatives: • Can do all combinations: ... f x x x i1 i2 ik • Order does not matter for f Ck Hessian Matrix Higher order Derivatives: • Important special case: Second order derivative 2 2 x1 x2 x1 xn x1 2 2 f (x) : H (x) x1 x2 x1 xn x2 f 2 x x x x x 2 1 n 2 n n • “Hessian” matrix (symmetric for f C2) • Orthogonal Eigenbasis, full Eigenspectrum Taylor Approximation f(x) x 2nd order approximation x1 (schematic) x2 Second order Taylor approximation: • Fit a paraboloid to a general function 1 f (x) f (x ) f (x )(x x ) (x x )T H (x )(x x ) 0 0 0 2 0 f 0 0 Special Cases Derivatives for: t y • Functions f: n (“heightfield”) z • Functions f: n (“curves”) • Functions f: n m (general case) x curves Derivatives of Curves Derivatives of vector valued functions: • Given a function f: n (“curve”) f1(t) f (t) fn(t) • We can compute derivatives for every output dimension: d f (t) dt 1 d f (t): : f '(t) : f (t) dt d f (t) n dt Geometric Meaning f(t) t0 f ’(t ) Tangent Vector: 0 • f ’: tangent vector . • Motion of physical particle: f = velocity. • Higher order derivatives: Again vector functions .. • Second derivative f = acceleration Special Cases Derivatives for: w y • Functions f: n (“heightfield”) u z • Functions f: n (“curves”) v x • Functions f: n m (general case) general mapping You can combine it... General case: • Given a function f: n m (“space warp”) f (x ,..., x ) 1 1 n f (x) f (x1 ,..., xn ) fm(x1 ,..., xn ) • Maps points in space to other points in space • First derivative: Derivatives of all output components of f w.r.t. all input directions. • “Jacobian matrix”: denoted by f or Jf Jacobian Matrix Jacobian Matrix: f (x) J f (x) f (x1 ,..., xn ) f (x ,..., x )T f (x) f (x) 1 1 n x1 1 xn 1 f (x ,..., x )T f (x) f (x) m 1 n x1 m xn m Use in a first-order Taylor approximation: f(x) f(x0 ) J f (x0 )x x0 matrix / vector product Special Cases Derivatives for: • Functions f: n (“heightfield”) • Functions f: n (“curves”) • Functions f: n m (general case) w f(x, y) t y y u z x2 v z x1 x x height field curves general mapping Coordinate Systems Problem: • What happens, if the coordinate system changes? • Partial derivatives go into different directions then. • Do we get the same result? Total Derivative First order Taylor approx.: f (x0 ) f (x0 )(x x0 ) • f (x ) f (x )(x x ) R (x) 0 0 0 x0 f(x) • Converges for C1 functions x0 f: n m x1 R (x) x2 lim x0 0, xx 0 x x0 (“totally differentiable”) Partial Derivatives Consequences: • A linear function: fully determined by image of a basis • Hence: Directions of partial derivatives do not matter – this is just a basis transform. We can use any linear independent set of directions T . Transform to standard basis by multiplying with T-1 • Similar argument for higher order derivatives Directional Derivative The directional derivative is defined as: • Given f: n m and v n, ||v|| = 1. • Directional derivative: f d v f (x) (x): f (x tv) v dt • Compute from Jacobian matrix v v f (x) f (x) v (requires total differentiability) Multi-Dimensional Integrals Integral Integral of a function • Function f: b • Integral f ( t ) dt measures signed area under curve: a + + + + + + -- Integral Numerical Approximation • Sum up a series of approximate shapes • (Riemannian) Definition: limit for baseline zero Multi-Dimensional Integral Integration in higher dimensions • Functions f: n • Tessellate domain and sum up volume of cuboids 1,4 1,4 1,2 1,2 1 1 0,8 0,8 0,6 0,6 0,4 0,4 1 1 0,2 0,8 0,2 0,8 0,6 0,6 0 0,4 0 0,4 0,2 0 0,1 0,2 0 0,1 0,2 0,3 0,2 0,3 0,4 0,5 0,4 0,5 0 0,6 0 0,6 0,7 0,8 0,7 0,8 0,9 1 0,9 1 Integral Transformations Integration by substitution: f(x) b g1(b) f (x)dx f (g(t))g'(t)dt 1 a g (a) Need to compensate for speed of f(x) movement that shrinks the measured area. g(x) g(x) Multi-Dimensional Substitution Transformation of Integrals: 2g(x) x f (x)dx f g(y) detg(y) dy 2 g1() • g C1, invertible 1g(x) • Jacobian approximates x1 local behavior of g() • Determinant: local area/volume change • In particular: det ( g ( y ) ) 1 means g() is area/volume conserving. Topology - a very short primer - A Few Concepts from Topology Homeomorphism: • 푓: 푋 → 푌 • 푓 is bijective • 푓 is continuous • 푓−1 exists and is continuous • Basically, a continuous deformation Topological equivalence • Objects are topologically equivalence if there exists a homeomorphism that maps between them • “Can be deformed into each other” Surfaces Boundaries of volumes in 3D • Topological Equivalence classes . Sphere . Torus . n-fold Torus • Genus = number of tunnels ... g = 0 g = 1 g = 2 Manifold homeomorphism 푥1 푥2 Definition: Manifold • A d-manifold M: At every 푥 ∈ 푀 there exists an 휖-environment homeomorphic to a d-dimensional disc • With boundary: disc or half-disc Further concepts Connected Set • There exists a continuous curve within the set between all pairs of points Simply Connected • Every closed loop can be continuously shrunken until it disappears Differential Geometry of Curves & Surfaces Part I: Curves Parametric Curves Parametric Curves: b C = f ((a, b)) • A differentiable function ff f: (a, b) n a describes a parametric curve n C = f ((a, b)), C . • The parametrization is called regular if f ’(t) 0 for all t. • If || f ’( t )| | 1 for all t, f is called a unit-speed parametrization of the curve C. Length of a Curve The length of a curve: • The length of a regular curve C is defined as: b length C f ' (t ) dt a • Independent of the parametrization (integral transformation theorem). • Alternative: lengthC = |b – a| for a unit-speed parametrization Reparametrization Enforcing unit-speed parametrization: • Assume:|| f ’( t )| | 0 for all t. • We have: x length C ( x ) f ' (t ) dt (invertible, because f ’(t) > 0) a • Concatenating f o length 1 yields a unit-speed parametrization of the curve length(t) length-1(t) Tangents Unit Tangents: • The unit tangent vector at x (a, b) is given by: f '(t) tangent(t) f '(t) 2 • For curves C , the unit normal vector of the curve is defined as: 0 1 f '(t) normal(t) 1 0 f '(t) Curvature Curvature: • First derivatives: curve direction / speed. • Curvature encoded in 2nd order information. • Why not just use f ’’? • Problem: Depends on parametrization . Different velocity yields different results . Need to distinguish between acceleration in tangential and non-tangential directions. Curvature & 2nd Derivatives C = f ((a, b)) normal(t) f’’(t) tangent(t) Definition of curvature • We want only the non-tangential component of f ’’. • Accelerating/slowing down does not matter for curvature of the traced out curve C. • Need to normalize speed. Curvature Curvature of a Curve C 2: 0 1 f ''(t), f '(t) 1 0 κ2(t) 3 f '(t) • Normalization factor: . Divide by || f ’|| to obtain unit tangent vector .
Load more

Recommended publications
  • DISCRETE DIFFERENTIAL GEOMETRY: an APPLIED INTRODUCTION Keenan Crane • CMU 15-458/858 LECTURE 15: CURVATURE
    DISCRETE DIFFERENTIAL GEOMETRY: AN APPLIED INTRODUCTION Keenan Crane • CMU 15-458/858 LECTURE 15: CURVATURE DISCRETE DIFFERENTIAL GEOMETRY: AN APPLIED INTRODUCTION Keenan Crane • CMU 15-458/858 Curvature—Overview • Intuitively, describes “how much a shape bends” – Extrinsic: how quickly does the tangent plane/normal change? – Intrinsic: how much do quantities differ from flat case? N T B Curvature—Overview • Driving force behind wide variety of physical phenomena – Objects want to reduce—or restore—their curvature – Even space and time are driven by curvature… Curvature—Overview • Gives a coordinate-invariant description of shape – fundamental theorems of plane curves, space curves, surfaces, … • Amazing fact: curvature gives you information about global topology! – “local-global theorems”: turning number, Gauss-Bonnet, … Curvature—Overview • Geometric algorithms: shape analysis, local descriptors, smoothing, … • Numerical simulation: elastic rods/shells, surface tension, … • Image processing algorithms: denoising, feature/contour detection, … Thürey et al 2010 Gaser et al Kass et al 1987 Grinspun et al 2003 Curvature of Curves Review: Curvature of a Plane Curve • Informally, curvature describes “how much a curve bends” • More formally, the curvature of an arc-length parameterized plane curve can be expressed as the rate of change in the tangent Equivalently: Here the angle brackets denote the usual dot product, i.e., . Review: Curvature and Torsion of a Space Curve •For a plane curve, curvature captured the notion of “bending” •For a space curve we also have torsion, which captures “twisting” Intuition: torsion is “out of plane bending” increasing torsion Review: Fundamental Theorem of Space Curves •The fundamental theorem of space curves tells that given the curvature κ and torsion τ of an arc-length parameterized space curve, we can recover the curve (up to rigid motion) •Formally: integrate the Frenet-Serret equations; intuitively: start drawing a curve, bend & twist at prescribed rate.
    [Show full text]
  • J.M. Sullivan, TU Berlin A: Curves Diff Geom I, SS 2019 This Course Is an Introduction to the Geometry of Smooth Curves and Surf
    J.M. Sullivan, TU Berlin A: Curves Diff Geom I, SS 2019 This course is an introduction to the geometry of smooth if the velocity never vanishes). Then the speed is a (smooth) curves and surfaces in Euclidean space Rn (in particular for positive function of t. (The cusped curve β above is not regular n = 2; 3). The local shape of a curve or surface is described at t = 0; the other examples given are regular.) in terms of its curvatures. Many of the big theorems in the DE The lengthR [ : Länge] of a smooth curve α is defined as subject – such as the Gauss–Bonnet theorem, a highlight at the j j len(α) = I α˙(t) dt. (For a closed curve, of course, we should end of the semester – deal with integrals of curvature. Some integrate from 0 to T instead of over the whole real line.) For of these integrals are topological constants, unchanged under any subinterval [a; b] ⊂ I, we see that deformation of the original curve or surface. Z b Z b We will usually describe particular curves and surfaces jα˙(t)j dt ≥ α˙(t) dt = α(b) − α(a) : locally via parametrizations, rather than, say, as level sets. a a Whereas in algebraic geometry, the unit circle is typically be described as the level set x2 + y2 = 1, we might instead This simply means that the length of any curve is at least the parametrize it as (cos t; sin t). straight-line distance between its endpoints. Of course, by Euclidean space [DE: euklidischer Raum] The length of an arbitrary curve can be defined (following n we mean the vector space R 3 x = (x1;:::; xn), equipped Jordan) as its total variation: with with the standard inner product or scalar product [DE: P Xn Skalarproduktp ] ha; bi = a · b := aibi and its associated norm len(α):= TV(α):= sup α(ti) − α(ti−1) : jaj := ha; ai.
    [Show full text]
  • Differential Geometry: Curvature and Holonomy Austin Christian
    University of Texas at Tyler Scholar Works at UT Tyler Math Theses Math Spring 5-5-2015 Differential Geometry: Curvature and Holonomy Austin Christian Follow this and additional works at: https://scholarworks.uttyler.edu/math_grad Part of the Mathematics Commons Recommended Citation Christian, Austin, "Differential Geometry: Curvature and Holonomy" (2015). Math Theses. Paper 5. http://hdl.handle.net/10950/266 This Thesis is brought to you for free and open access by the Math at Scholar Works at UT Tyler. It has been accepted for inclusion in Math Theses by an authorized administrator of Scholar Works at UT Tyler. For more information, please contact [email protected]. DIFFERENTIAL GEOMETRY: CURVATURE AND HOLONOMY by AUSTIN CHRISTIAN A thesis submitted in partial fulfillment of the requirements for the degree of Master of Science Department of Mathematics David Milan, Ph.D., Committee Chair College of Arts and Sciences The University of Texas at Tyler May 2015 c Copyright by Austin Christian 2015 All rights reserved Acknowledgments There are a number of people that have contributed to this project, whether or not they were aware of their contribution. For taking me on as a student and learning differential geometry with me, I am deeply indebted to my advisor, David Milan. Without himself being a geometer, he has helped me to develop an invaluable intuition for the field, and the freedom he has afforded me to study things that I find interesting has given me ample room to grow. For introducing me to differential geometry in the first place, I owe a great deal of thanks to my undergraduate advisor, Robert Huff; our many fruitful conversations, mathematical and otherwise, con- tinue to affect my approach to mathematics.
    [Show full text]
  • Lines of Curvature on Surfaces, Historical Comments and Recent Developments
    S˜ao Paulo Journal of Mathematical Sciences 2, 1 (2008), 99–143 Lines of Curvature on Surfaces, Historical Comments and Recent Developments Jorge Sotomayor Instituto de Matem´atica e Estat´ıstica, Universidade de S˜ao Paulo, Rua do Mat˜ao 1010, Cidade Universit´aria, CEP 05508-090, S˜ao Paulo, S.P., Brazil Ronaldo Garcia Instituto de Matem´atica e Estat´ıstica, Universidade Federal de Goi´as, CEP 74001-970, Caixa Postal 131, Goiˆania, GO, Brazil Abstract. This survey starts with the historical landmarks leading to the study of principal configurations on surfaces, their structural sta- bility and further generalizations. Here it is pointed out that in the work of Monge, 1796, are found elements of the qualitative theory of differential equations ( QTDE ), founded by Poincar´ein 1881. Here are also outlined a number of recent results developed after the assimilation into the subject of concepts and problems from the QTDE and Dynam- ical Systems, such as Structural Stability, Bifurcations and Genericity, among others, as well as extensions to higher dimensions. References to original works are given and open problems are proposed at the end of some sections. 1. Introduction The book on differential geometry of D. Struik [79], remarkable for its historical notes, contains key references to the classical works on principal curvature lines and their umbilic singularities due to L. Euler [8], G. Monge [61], C. Dupin [7], G. Darboux [6] and A. Gullstrand [39], among others (see The authors are fellows of CNPq and done this work under the project CNPq 473747/2006-5. The authors are grateful to L.
    [Show full text]
  • Surface Integrals
    VECTOR CALCULUS 16.7 Surface Integrals In this section, we will learn about: Integration of different types of surfaces. PARAMETRIC SURFACES Suppose a surface S has a vector equation r(u, v) = x(u, v) i + y(u, v) j + z(u, v) k (u, v) D PARAMETRIC SURFACES •We first assume that the parameter domain D is a rectangle and we divide it into subrectangles Rij with dimensions ∆u and ∆v. •Then, the surface S is divided into corresponding patches Sij. •We evaluate f at a point Pij* in each patch, multiply by the area ∆Sij of the patch, and form the Riemann sum mn * f() Pij S ij ij11 SURFACE INTEGRAL Equation 1 Then, we take the limit as the number of patches increases and define the surface integral of f over the surface S as: mn * f( x , y , z ) dS lim f ( Pij ) S ij mn, S ij11 . Analogues to: The definition of a line integral (Definition 2 in Section 16.2);The definition of a double integral (Definition 5 in Section 15.1) . To evaluate the surface integral in Equation 1, we approximate the patch area ∆Sij by the area of an approximating parallelogram in the tangent plane. SURFACE INTEGRALS In our discussion of surface area in Section 16.6, we made the approximation ∆Sij ≈ |ru x rv| ∆u ∆v where: x y z x y z ruv i j k r i j k u u u v v v are the tangent vectors at a corner of Sij. SURFACE INTEGRALS Formula 2 If the components are continuous and ru and rv are nonzero and nonparallel in the interior of D, it can be shown from Definition 1—even when D is not a rectangle—that: fxyzdS(,,) f ((,))|r uv r r | dA uv SD SURFACE INTEGRALS This should be compared with the formula for a line integral: b fxyzds(,,) f (())|'()|rr t tdt Ca Observe also that: 1dS |rr | dA A ( S ) uv SD SURFACE INTEGRALS Example 1 Compute the surface integral x2 dS , where S is the unit sphere S x2 + y2 + z2 = 1.
    [Show full text]
  • Geodetic Position Computations
    GEODETIC POSITION COMPUTATIONS E. J. KRAKIWSKY D. B. THOMSON February 1974 TECHNICALLECTURE NOTES REPORT NO.NO. 21739 PREFACE In order to make our extensive series of lecture notes more readily available, we have scanned the old master copies and produced electronic versions in Portable Document Format. The quality of the images varies depending on the quality of the originals. The images have not been converted to searchable text. GEODETIC POSITION COMPUTATIONS E.J. Krakiwsky D.B. Thomson Department of Geodesy and Geomatics Engineering University of New Brunswick P.O. Box 4400 Fredericton. N .B. Canada E3B5A3 February 197 4 Latest Reprinting December 1995 PREFACE The purpose of these notes is to give the theory and use of some methods of computing the geodetic positions of points on a reference ellipsoid and on the terrain. Justification for the first three sections o{ these lecture notes, which are concerned with the classical problem of "cCDputation of geodetic positions on the surface of an ellipsoid" is not easy to come by. It can onl.y be stated that the attempt has been to produce a self contained package , cont8.i.ning the complete development of same representative methods that exist in the literature. The last section is an introduction to three dimensional computation methods , and is offered as an alternative to the classical approach. Several problems, and their respective solutions, are presented. The approach t~en herein is to perform complete derivations, thus stqing awrq f'rcm the practice of giving a list of for11111lae to use in the solution of' a problem.
    [Show full text]
  • On the Patterns of Principal Curvature Lines Around a Curve of Umbilic Points
    Anais da Academia Brasileira de Ciências (2005) 77(1): 13–24 (Annals of the Brazilian Academy of Sciences) ISSN 0001-3765 www.scielo.br/aabc On the Patterns of Principal Curvature Lines around a Curve of Umbilic Points RONALDO GARCIA1 and JORGE SOTOMAYOR2 1Instituto de Matemática e Estatística, Universidade Federal de Goiás Caixa Postal 131 – 74001-970 Goiânia, GO, Brasil 2Instituto de Matemática e Estatística, Universidade de São Paulo Rua do Matão 1010, Cidade Universitária, 05508-090 São Paulo, SP, Brasil Manuscript received on June 15, 2004; accepted for publication on October 10, 2004; contributed by Jorge Sotomayor* ABSTRACT In this paper is studied the behavior of principal curvature lines near a curve of umbilic points of a smooth surface. Key words: Umbilic point, principal curvature lines, principal cycles. 1 INTRODUCTION The study of umbilic points on surfaces and the patterns of principal curvature lines around them has attracted the attention of generation of mathematicians among whom can be named Monge, Darboux and Carathéodory. One aspect – concerning isolated umbilics – of the contributions of these authors, departing from Darboux (Darboux 1896), has been elaborated and extended in several directions by Garcia, Sotomayor and Gutierrez, among others. See (Gutierrez and Sotomayor, 1982, 1991, 1998), (Garcia and Sotomayor, 1997, 2000) and (Garcia et al. 2000, 2004) where additional references can be found. In (Carathéodory 1935) Carathéodory mentioned the interest of non isolated umbilics in generic surfaces pertinent to Geometric Optics. In a remarkably concise study he established that any local analytic regular arc of curve in R3 is a curve of umbilic points of a piece of analytic surface.
    [Show full text]
  • 16.6 Parametric Surfaces and Their Areas
    CHAPTER 16. VECTOR CALCULUS 239 16.6 Parametric Surfaces and Their Areas Comments. On the next page we summarize some ways of looking at graphs in Calc I, Calc II, and Calc III, and pose a question about what comes next. 2 3 2 Definition. Let r : R ! R and let D ⊆ R . A parametric surface S is the set of all points hx; y; zi such that hx; y; zi = r(u; v) for some hu; vi 2 D. In other words, it's the set of points you get using x = some function of u; v y = some function of u; v z = some function of u; v Example 1. (a) Describe the surface z = −x2 − y2 + 2 over the region D : −1 ≤ x ≤ 1; −1 ≤ y ≤ 1 as a parametric surface. Graph it in MATLAB. (b) Describe the surface z = −x2 − y2 + 2 over the region D : x2 + y2 ≤ 1 as a parametric surface. Graph it in MATLAB. Solution: (a) In this case we \cheat": we already have z as a function of x and y, so anything we do to get rid of x and y will work x = u y = v z = −u2 − v2 + 2 −1 ≤ u ≤ 1; −1 ≤ v ≤ 1 [u,v]=meshgrid(linspace(-1,1,35)); x=u; y=v; z=2-u.^2-v.^2; surf(x,y,z) CHAPTER 16. VECTOR CALCULUS 240 How graphs look in different contexts: Pre-Calc, and Calc I graphs: Calc II parametric graphs: y = f(x) x = f(t), y = g(t) • 1 number gets plugged in (usually x) • 1 number gets plugged in (usually t) • 1 number comes out (usually y) • 2 numbers come out (x and y) • Graph is essentially one dimensional (if you zoom in enough it looks like a line, plus you only need • graph is essentially one dimensional (but we one number, x, to specify any location on the don't picture t at all) graph) • We need to picture the graph in two dimensional • We need to picture the graph in a two dimen- world.
    [Show full text]
  • Polynomial Curves and Surfaces
    Polynomial Curves and Surfaces Chandrajit Bajaj and Andrew Gillette September 8, 2010 Contents 1 What is an Algebraic Curve or Surface? 2 1.1 Algebraic Curves . .3 1.2 Algebraic Surfaces . .3 2 Singularities and Extreme Points 4 2.1 Singularities and Genus . .4 2.2 Parameterizing with a Pencil of Lines . .6 2.3 Parameterizing with a Pencil of Curves . .7 2.4 Algebraic Space Curves . .8 2.5 Faithful Parameterizations . .9 3 Triangulation and Display 10 4 Polynomial and Power Basis 10 5 Power Series and Puiseux Expansions 11 5.1 Weierstrass Factorization . 11 5.2 Hensel Lifting . 11 6 Derivatives, Tangents, Curvatures 12 6.1 Curvature Computations . 12 6.1.1 Curvature Formulas . 12 6.1.2 Derivation . 13 7 Converting Between Implicit and Parametric Forms 20 7.1 Parameterization of Curves . 21 7.1.1 Parameterizing with lines . 24 7.1.2 Parameterizing with Higher Degree Curves . 26 7.1.3 Parameterization of conic, cubic plane curves . 30 7.2 Parameterization of Algebraic Space Curves . 30 7.3 Automatic Parametrization of Degree 2 Curves and Surfaces . 33 7.3.1 Conics . 34 7.3.2 Rational Fields . 36 7.4 Automatic Parametrization of Degree 3 Curves and Surfaces . 37 7.4.1 Cubics . 38 7.4.2 Cubicoids . 40 7.5 Parameterizations of Real Cubic Surfaces . 42 7.5.1 Real and Rational Points on Cubic Surfaces . 44 7.5.2 Algebraic Reduction . 45 1 7.5.3 Parameterizations without Real Skew Lines . 49 7.5.4 Classification and Straight Lines from Parametric Equations . 52 7.5.5 Parameterization of general algebraic plane curves by A-splines .
    [Show full text]
  • Riemannian Submanifolds: a Survey
    RIEMANNIAN SUBMANIFOLDS: A SURVEY BANG-YEN CHEN Contents Chapter 1. Introduction .............................. ...................6 Chapter 2. Nash’s embedding theorem and some related results .........9 2.1. Cartan-Janet’s theorem .......................... ...............10 2.2. Nash’s embedding theorem ......................... .............11 2.3. Isometric immersions with the smallest possible codimension . 8 2.4. Isometric immersions with prescribed Gaussian or Gauss-Kronecker curvature .......................................... ..................12 2.5. Isometric immersions with prescribed mean curvature. ...........13 Chapter 3. Fundamental theorems, basic notions and results ...........14 3.1. Fundamental equations ........................... ..............14 3.2. Fundamental theorems ............................ ..............15 3.3. Basic notions ................................... ................16 3.4. A general inequality ............................. ...............17 3.5. Product immersions .............................. .............. 19 3.6. A relationship between k-Ricci tensor and shape operator . 20 3.7. Completeness of curvature surfaces . ..............22 Chapter 4. Rigidity and reduction theorems . ..............24 4.1. Rigidity ....................................... .................24 4.2. A reduction theorem .............................. ..............25 Chapter 5. Minimal submanifolds ....................... ...............26 arXiv:1307.1875v1 [math.DG] 7 Jul 2013 5.1. First and second variational formulas
    [Show full text]
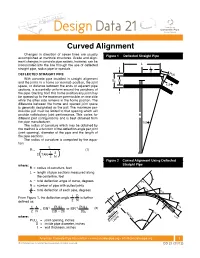
  • Design Data 21
    Design Data 21 Curved Alignment Changes in direction of sewer lines are usually Figure 1 Deflected Straight Pipe accomplished at manhole structures. Grade and align- Figure 1 Deflected Straight Pipe ment changes in concrete pipe sewers, however, can be incorporated into the line through the use of deflected L straight pipe, radius pipe or specials. t L 2 DEFLECTED STRAIGHT PIPE Pull With concrete pipe installed in straight alignment Bc D and the joints in a home (or normal) position, the joint ∆ space, or distance between the ends of adjacent pipe 1/2 N sections, is essentially uniform around the periphery of the pipe. Starting from this home position any joint may t be opened up to the maximum permissible on one side while the other side remains in the home position. The difference between the home and opened joint space is generally designated as the pull. The maximum per- missible pull must be limited to that opening which will provide satisfactory joint performance. This varies for R different joint configurations and is best obtained from the pipe manufacturer. ∆ 1/2 N The radius of curvature which may be obtained by this method is a function of the deflection angle per joint (joint opening), diameter of the pipe and the length of the pipe sections. The radius of curvature is computed by the equa- tion: L R = (1) 1 ∆ 2 TAN ( 2 N ) Figure 2 Curved Alignment Using Deflected Figure 2 Curved Alignment Using Deflected where: Straight Pipe R = radius of curvature, feet Straight Pipe L = length of pipe sections measured along the centerline, feet ∆ ∆ = total deflection angle of curve, degrees P.I.
    [Show full text]
  • Basics of the Differential Geometry of Surfaces
    Chapter 20 Basics of the Differential Geometry of Surfaces 20.1 Introduction The purpose of this chapter is to introduce the reader to some elementary concepts of the differential geometry of surfaces. Our goal is rather modest: We simply want to introduce the concepts needed to understand the notion of Gaussian curvature, mean curvature, principal curvatures, and geodesic lines. Almost all of the material presented in this chapter is based on lectures given by Eugenio Calabi in an upper undergraduate differential geometry course offered in the fall of 1994. Most of the topics covered in this course have been included, except a presentation of the global Gauss–Bonnet–Hopf theorem, some material on special coordinate systems, and Hilbert’s theorem on surfaces of constant negative curvature. What is a surface? A precise answer cannot really be given without introducing the concept of a manifold. An informal answer is to say that a surface is a set of points in R3 such that for every point p on the surface there is a small (perhaps very small) neighborhood U of p that is continuously deformable into a little flat open disk. Thus, a surface should really have some topology. Also,locally,unlessthe point p is “singular,” the surface looks like a plane. Properties of surfaces can be classified into local properties and global prop- erties.Intheolderliterature,thestudyoflocalpropertieswascalled geometry in the small,andthestudyofglobalpropertieswascalledgeometry in the large.Lo- cal properties are the properties that hold in a small neighborhood of a point on a surface. Curvature is a local property. Local properties canbestudiedmoreconve- niently by assuming that the surface is parametrized locally.
    [Show full text]