DOCSLIB.ORG

J.M. Sullivan, TU Berlin A: Curves Diff Geom I, SS 2019 This Course Is an Introduction to the Geometry of Smooth Curves and Surf

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
J.M. Sullivan, TU Berlin A: Curves Diff Geom I, SS 2019 This Course Is an Introduction to the Geometry of Smooth Curves and Surf J.M. Sullivan, TU Berlin A: Curves Diff Geom I, SS 2019 This course is an introduction to the geometry of smooth if the velocity never vanishes). Then the speed is a (smooth) curves and surfaces in Euclidean space Rn (in particular for positive function of t. (The cusped curve β above is not regular n = 2; 3). The local shape of a curve or surface is described at t = 0; the other examples given are regular.) in terms of its curvatures. Many of the big theorems in the DE The lengthR [ : Länge] of a smooth curve α is defined as subject – such as the Gauss–Bonnet theorem, a highlight at the j j len(α) = I α˙(t) dt. (For a closed curve, of course, we should end of the semester – deal with integrals of curvature. Some integrate from 0 to T instead of over the whole real line.) For of these integrals are topological constants, unchanged under any subinterval [a; b] ⊂ I, we see that deformation of the original curve or surface. Z b Z b We will usually describe particular curves and surfaces jα˙(t)j dt ≥ α˙(t) dt = α(b) − α(a) : locally via parametrizations, rather than, say, as level sets. a a Whereas in algebraic geometry, the unit circle is typically be described as the level set x2 + y2 = 1, we might instead This simply means that the length of any curve is at least the parametrize it as (cos t; sin t). straight-line distance between its endpoints. Of course, by Euclidean space [DE: euklidischer Raum] The length of an arbitrary curve can be defined (following n we mean the vector space R 3 x = (x1;:::; xn), equipped Jordan) as its total variation: with with the standard inner product or scalar product [DE: P Xn Skalarproduktp ] ha; bi = a · b := aibi and its associated norm len(α):= TV(α):= sup α(ti) − α(ti−1) : jaj := ha; ai. ··· 2 t0< <tn I i=1 This is the supremal length of inscribed polygons. (One can A. CURVES show this Jordan length is finite over finite intervals if and only if α has a Lipschitz reparametrization, e.g., by arclength. For Given any interval I ⊂ R, a continuous map α: I ! Rn a Lipschitz curve, the velocity is defined almost everywhere, is called a (parametrized) curve [DE: parametrisierte Kurve] so the integrals we used above – giving displacement as the n in R . We write α(t) =: α1(t); : : : ; αn(t) : integral of velocity and length as the integral of speed – exist We say α is Ck if it has continuous derivatives of order up in the sense of Lebesgue.) to k. Here of course C0 means nothing more than continuous, If J is another interval and ': J ! I is an orientation- while C1 is a minimal degree of smoothness, which is insuffi- preserving homeomorphism, i.e., a strictly increasing surjec- cient for many of our purposes. Indeed, for this course, rather tion, then α◦': J ! Rn is a parametrized curve with the same than tracking which results require, say, C2 or C3 smoothness, image (or trace) as α, called a reparametrization of α. (Note we will use smooth [DE: glatt] to mean C1 and will typically that the reverse curveα ¯ : − I ! Rn, defined byα ¯(t):= α(−t), assume that all of our curves are smooth. traces the same image in reverse order; this could be called an Examples (parametrized on I = R): orientation-reversing reparametrization.) 3 When studying arbitrary continuous curves, it’s sometimes • α(t):= (a cos t; a sin t; bt) is a helix in R (for a; b , 0); helpful to allow more general reparametrizations via ': J ! I • β(t):= (t2; t3) is a smooth parametrization of a plane which is monotonic but not strictly monotonic. That is, we curve with a cusp; allow a reparametrization that stops at one point for a while – or that removes such a constant interval. • γ(t):= (sin t; sin 2t) is a figure-8 curve in R2; We instead focus on regular smooth curves α. Then if ': J ! I is a diffeomorphism [DE: Diffeomorphismus] 2 n n • µ(t):= (t; t ;:::; t ) is called the moment curve in R . (a smooth map with nonvanishing derivative, so that '−1 is also smooth) then α ◦ ' is again smooth and regular. A simple curve [DE: einfache Kurve] is one where the map We are interested in properties invariant under such smooth α: I ! Rn is injective. A closed curve [DE: geschlossene reparametrizations. Declaring a (regular smooth) curve to Kurve] is one where α: R ! Rn is T-periodic for some T > 0, be equivalent to any smooth reparametrization, this gives an meaning α(t + T) = α(T) for all t 2 R. Of course no closed equivalence relation on the space of all parametrized curves. curve is simple in the above sense; instead we define a sim- Formally, we could define an unparametrized (smooth) curve ple closed curve [DE: einfach geschlossene Kurve] as a closed as an equivalence class. These are really the objects we curve where α is injective on the half-open interval [0; T). want to study, but we do so implicitly, using parametrized A smooth (or even just C1) curve α has a velocity vector curves and focusing on properties that are independent of [DE: Geschwindigkeitsvektor]α ˙(t) 2 Rn at each point. The parametrization, switching to a different parametrization fundamental theorem of calculus says this velocity can be in- when convenient. tegrated to give the displacement vector For a fixed t0 2 I we define the arclength function s(t):= R t Z b jα˙(t)j dt. Here s maps I to an interval J of length len(α). If t0 α˙(t) dt = α(b) − α(a): α is a regular smooth curve, then s(t) is smooth, with positive a derivatives ˙ = jα˙j > 0 equal to the speed. Thus it has a smooth The speed [DE: Bahngeschwindigkeit] of α is jα˙(t)j ≥ 0. We inverse function ': J ! I. We say β = α ◦ ' is the arclength say α is regular [DE: regulär] if the speed is positive (that is, parametrization [DE: Parametrisierung nach Bogenlänge] (or 1 J.M. Sullivan, TU Berlin A: Curves Diff Geom I, SS 2019 unit-speed parametrization) of α. We have β(s) = α('(s)), In particular, if v ? w (i.e., v · w ≡ 0) then v0 · w = −w0 · v. so β(s(t)) = α('(s(t))) = α(t). It follows that β has constant And if jvj is constant then v0 ? v. (Geometrically, this is just speed 1, and thus that the arclength of βj[a;b] is b − a. saying that the tangent plane to a sphere is perpendicular to The arclength parametetrization is hard to write down ex- the radius vector.) In particular, we have ~κ ? T. plicitly for most examples – we have to integrate a square root, Example: the circle α(t) = (r cos t; r sin t) of radius r then invert the resulting function. (There has been some work (parametrized here with constant speed r) has in computer-aided design on so-called “pythagorean hodo- graph curves”, curves with rational parametrizations whose −1 T = (− sin t; cos t); ~κ = (cos t; sin t); κ ≡ 1=r: speed is also a rational function, with no square root. But this r still doesn’t get us all the way to a unit-speed parametrization.) The fact that the arclength parametrization always exists, Given regular smooth parametrization α with speed σ := however, means that we can use it when proving theorems, s˙ = jα˙j, the velocity is σT, so the acceleration vector is and this is usually easiest. (Even when considering curves with less smoothness, e.g., Ck, there is a general principle α¨ = σT· = σ˙ T + σT˙ = σ˙ T + σ2T 0 = σ˙ T + σ2~κ: that no regular parametrization is smoother than the arclength parametrization.) Solving for ~κ we get the formula Although for an arbitrary parameter we have used the name t (thinking of time) and written d=dt with a dot, when we use hα,¨ α˙i α˙ jα˙j2 ~κ = α¨ − hα,¨ Ti T = α¨ − the arclength parametrization, we’ll call the parameter s and jα˙j2 write d=ds with a prime. Of course, for any function f along the curve, the chain rule says for the curvature of a curve not necessarily parametrized at unit speed. d f ds d f n = ; i.e., f 0 = f˙=s˙ = f˙=jα˙j: Any three distinct points in R lie on a unique circle (or ds dt dt line). The osculating circle to α at p is the limit of such circles through three points along α approaching p. It is also the limit Suppose now that α is a regular smooth unit-speed curve. of circles tangent to α at p and passing through another point Then its velocity α0 is everywhere a unit vector, the (unit) tan- of the curve approaching p. Again, one can investigate the gent vector [DE: Tangenten(einheits)vektor] T(s):= α0(s) to exact degree of smoothness required to have such limits exist. the curve. (In terms of an arbitrary regular parametrization, we have of course T = α/˙ jα˙j.) Note that the second-order Taylor series for a unit-speed curve around the point p = α(0) (we assume without further End of Lecture 8 Apr 2019 comment that 0 2 I) is: We should best think of T(s) as a vector based at p = α(s), perhaps as an arrow from p to p + T(s), rather than as a point s2 α(s) = p + sT(0) + ~κ(0) + O(s3): in Rn.
Load more

Recommended publications
  • Abstract Book
    14th International Geometry Symposium 25-28 May 2016 ABSTRACT BOOK Pamukkale University Denizli - TURKEY 1 14th International Geometry Symposium Pamukkale University Denizli/TURKEY 25-28 May 2016 14th International Geometry Symposium ABSTRACT BOOK 1 14th International Geometry Symposium Pamukkale University Denizli/TURKEY 25-28 May 2016 Proceedings of the 14th International Geometry Symposium Edited By: Dr. Şevket CİVELEK Dr. Cansel YORMAZ E-Published By: Pamukkale University Department of Mathematics Denizli, TURKEY All rights reserved. No part of this publication may be reproduced in any material form (including photocopying or storing in any medium by electronic means or whether or not transiently or incidentally to some other use of this publication) without the written permission of the copyright holder. Authors of papers in these proceedings are authorized to use their own material freely. Applications for the copyright holder’s written permission to reproduce any part of this publication should be addressed to: Assoc. Prof. Dr. Şevket CİVELEK Pamukkale University Department of Mathematics Denizli, TURKEY Email: [email protected] 2 14th International Geometry Symposium Pamukkale University Denizli/TURKEY 25-28 May 2016 Proceedings of the 14th International Geometry Symposium May 25-28, 2016 Denizli, Turkey. Jointly Organized by Pamukkale University Department of Mathematics Denizli, Turkey 3 14th International Geometry Symposium Pamukkale University Denizli/TURKEY 25-28 May 2016 PREFACE This volume comprises the abstracts of contributed papers presented at the 14th International Geometry Symposium, 14IGS 2016 held on May 25-28, 2016, in Denizli, Turkey. 14IGS 2016 is jointly organized by Department of Mathematics, Pamukkale University, Denizli, Turkey. The sysposium is aimed to provide a platform for Geometry and its applications.
    [Show full text]
  • Two Exotic Holonomies in Dimension Four, Path Geometries, and Twistor Theory
    Two Exotic Holonomies in Dimension Four, Path Geometries, and Twistor Theory by Robert L. Bryant* Table of Contents §0. Introduction §1. The Holonomy of a Torsion-Free Connection §2. The Structure Equations of H3-andG3-structures §3. The Existence Theorems §4. Path Geometries and Exotic Holonomy §5. Twistor Theory and Exotic Holonomy §6. Epilogue §0. Introduction Since its introduction by Elie´ Cartan, the holonomy of a connection has played an important role in differential geometry. One of the best known results concerning hol- onomy is Berger’s classification of the possible holonomies of Levi-Civita connections of Riemannian metrics. Since the appearance of Berger [1955], much work has been done to refine his listofpossible Riemannian holonomies. See the recent works by Besse [1987]or Salamon [1989]foruseful historical surveys and applications of holonomy to Riemannian and algebraic geometry. Less well known is that, at the same time, Berger also classified the possible pseudo- Riemannian holonomies which act irreducibly on each tangent space. The intervening years have not completely resolved the question of whether all of the subgroups of the general linear group on his pseudo-Riemannian list actually occur as holonomy groups of pseudo-Riemannian metrics, but, as of this writing, only one class of examples on his list remains in doubt, namely SO∗(2p) ⊂ GL(4p)forp ≥ 3. Perhaps the least-known aspect of Berger’s work on holonomy concerns his list of the possible irreducibly-acting holonomy groups of torsion-free affine connections. (Torsion- free connections are the natural generalization of Levi-Civita connections in the metric case.) Part of the reason for this relative obscurity is that affine geometry is not as well known or widely usedasRiemannian geometry and global results are generally lacking.
    [Show full text]
  • Differential Geometry: Curvature and Holonomy Austin Christian
    University of Texas at Tyler Scholar Works at UT Tyler Math Theses Math Spring 5-5-2015 Differential Geometry: Curvature and Holonomy Austin Christian Follow this and additional works at: https://scholarworks.uttyler.edu/math_grad Part of the Mathematics Commons Recommended Citation Christian, Austin, "Differential Geometry: Curvature and Holonomy" (2015). Math Theses. Paper 5. http://hdl.handle.net/10950/266 This Thesis is brought to you for free and open access by the Math at Scholar Works at UT Tyler. It has been accepted for inclusion in Math Theses by an authorized administrator of Scholar Works at UT Tyler. For more information, please contact [email protected]. DIFFERENTIAL GEOMETRY: CURVATURE AND HOLONOMY by AUSTIN CHRISTIAN A thesis submitted in partial fulfillment of the requirements for the degree of Master of Science Department of Mathematics David Milan, Ph.D., Committee Chair College of Arts and Sciences The University of Texas at Tyler May 2015 c Copyright by Austin Christian 2015 All rights reserved Acknowledgments There are a number of people that have contributed to this project, whether or not they were aware of their contribution. For taking me on as a student and learning differential geometry with me, I am deeply indebted to my advisor, David Milan. Without himself being a geometer, he has helped me to develop an invaluable intuition for the field, and the freedom he has afforded me to study things that I find interesting has given me ample room to grow. For introducing me to differential geometry in the first place, I owe a great deal of thanks to my undergraduate advisor, Robert Huff; our many fruitful conversations, mathematical and otherwise, con- tinue to affect my approach to mathematics.
    [Show full text]
  • Special Holonomy and Two-Dimensional Supersymmetric
    Special Holonomy and Two-Dimensional Supersymmetric σ-Models Vid Stojevic arXiv:hep-th/0611255v1 23 Nov 2006 Submitted for the Degree of Doctor of Philosophy Department of Mathematics King’s College University of London 2006 Abstract d = 2 σ-models describing superstrings propagating on manifolds of special holonomy are characterized by symmetries related to covariantly constant forms that these manifolds hold, which are generally non-linear and close in a field dependent sense. The thesis explores various aspects of the special holonomy symmetries (SHS). Cohomological equations are set up that enable a calculation of potential quantum anomalies in the SHS. It turns out that it’s necessary to linearize the algebras by treating composite currents as generators of additional symmetries. Surprisingly we find that for most cases the linearization involves a finite number of composite currents, with the exception of SU(3) and G2 which seem to allow no finite linearization. We extend the analysis to cases with torsion, and work out the implications of generalized Nijenhuis forms. SHS are analyzed on boundaries of open strings. Branes wrapping calibrated cycles of special holonomy manifolds are related, from the σ-model point of view, to the preser- vation of special holonomy symmetries on string boundaries. Some technical results are obtained, and specific cases with torsion and non-vanishing gauge fields are worked out. Classical W -string actions obtained by gauging the SHS are analyzed. These are of interest both as a gauge theories and for calculating operator product expansions. For many cases there is an obstruction to obtaining the BRST operator due to relations between SHS that are implied by Jacobi identities.
    [Show full text]
  • Geodetic Position Computations
    GEODETIC POSITION COMPUTATIONS E. J. KRAKIWSKY D. B. THOMSON February 1974 TECHNICALLECTURE NOTES REPORT NO.NO. 21739 PREFACE In order to make our extensive series of lecture notes more readily available, we have scanned the old master copies and produced electronic versions in Portable Document Format. The quality of the images varies depending on the quality of the originals. The images have not been converted to searchable text. GEODETIC POSITION COMPUTATIONS E.J. Krakiwsky D.B. Thomson Department of Geodesy and Geomatics Engineering University of New Brunswick P.O. Box 4400 Fredericton. N .B. Canada E3B5A3 February 197 4 Latest Reprinting December 1995 PREFACE The purpose of these notes is to give the theory and use of some methods of computing the geodetic positions of points on a reference ellipsoid and on the terrain. Justification for the first three sections o{ these lecture notes, which are concerned with the classical problem of "cCDputation of geodetic positions on the surface of an ellipsoid" is not easy to come by. It can onl.y be stated that the attempt has been to produce a self contained package , cont8.i.ning the complete development of same representative methods that exist in the literature. The last section is an introduction to three dimensional computation methods , and is offered as an alternative to the classical approach. Several problems, and their respective solutions, are presented. The approach t~en herein is to perform complete derivations, thus stqing awrq f'rcm the practice of giving a list of for11111lae to use in the solution of' a problem.
    [Show full text]
  • Curvatures of Smooth and Discrete Surfaces
    Curvatures of Smooth and Discrete Surfaces John M. Sullivan Abstract. We discuss notions of Gauss curvature and mean curvature for polyhedral surfaces. The discretizations are guided by the principle of preserving integral relations for curvatures, like the Gauss/Bonnet theorem and the mean-curvature force balance equation. Keywords. Discrete Gauss curvature, discrete mean curvature, integral curvature rela- tions. The curvatures of a smooth surface are local measures of its shape. Here we con- sider analogous quantities for discrete surfaces, meaning triangulated polyhedral surfaces. Often the most useful analogs are those which preserve integral relations for curvature, like the Gauss/Bonnet theorem or the force balance equation for mean curvature. For sim- plicity, we usually restrict our attention to surfaces in euclidean three-space E3, although some of the results generalize to other ambient manifolds of arbitrary dimension. This article is intended as background for some of the related contributions to this volume. Much of the material here is not new; some is even quite old. Although some references are given, no attempt has been made to give a comprehensive bibliography or a full picture of the historical development of the ideas. 1. Smooth curves, framings and integral curvature relations A companion article [Sul08] in this volume investigates curves of finite total curvature. This class includes both smooth and polygonal curves, and allows a unified treatment of curvature. Here we briefly review the theory of smooth curves from the point of view we will later adopt for surfaces. The curvatures of a smooth curve γ (which we usually assume is parametrized by its arclength s) are the local properties of its shape, invariant under euclidean motions.
    [Show full text]
  • Riemannian Submanifolds: a Survey
    RIEMANNIAN SUBMANIFOLDS: A SURVEY BANG-YEN CHEN Contents Chapter 1. Introduction .............................. ...................6 Chapter 2. Nash’s embedding theorem and some related results .........9 2.1. Cartan-Janet’s theorem .......................... ...............10 2.2. Nash’s embedding theorem ......................... .............11 2.3. Isometric immersions with the smallest possible codimension . 8 2.4. Isometric immersions with prescribed Gaussian or Gauss-Kronecker curvature .......................................... ..................12 2.5. Isometric immersions with prescribed mean curvature. ...........13 Chapter 3. Fundamental theorems, basic notions and results ...........14 3.1. Fundamental equations ........................... ..............14 3.2. Fundamental theorems ............................ ..............15 3.3. Basic notions ................................... ................16 3.4. A general inequality ............................. ...............17 3.5. Product immersions .............................. .............. 19 3.6. A relationship between k-Ricci tensor and shape operator . 20 3.7. Completeness of curvature surfaces . ..............22 Chapter 4. Rigidity and reduction theorems . ..............24 4.1. Rigidity ....................................... .................24 4.2. A reduction theorem .............................. ..............25 Chapter 5. Minimal submanifolds ....................... ...............26 arXiv:1307.1875v1 [math.DG] 7 Jul 2013 5.1. First and second variational formulas
    [Show full text]
  • Riemannian Holonomy and Algebraic Geometry
    Riemannian Holonomy and Algebraic Geometry Arnaud BEAUVILLE Revised version (March 2006) Introduction This survey is devoted to a particular instance of the interaction between Riemannian geometry and algebraic geometry, the study of manifolds with special holonomy. The holonomy group is one of the most basic objects associated with a Riemannian metric; roughly, it tells us what are the geometric objects on the manifold (complex structures, differential forms, ...) which are parallel with respect to the metric (see 1.3 for a precise statement). There are two surprising facts about this group. The first one is that, despite its very general definition, there are few possibilities – this is Berger’s theorem (1.2). The second one is that apart from the generic case in which the holonomy group is SO(n) , all other cases appear to be related in some way to algebraic geometry. Indeed the study of compact manifolds with special holonomy brings into play some special, and quite interesting, classes of algebraic varieties: Calabi-Yau, complex symplectic or complex contact manifolds. I would like to convince algebraic geometers that this interplay is interesting on two accounts: on one hand the general theorems on holonomy give deep results on the geometry of these special varieties; on the other hand Riemannian geometry provides us with good problems in algebraic geometry – see 4.3 for a typical example. I have tried to make these notes accessible to students with little knowledge of Riemannian geometry, and a basic knowledge of algebraic geometry. Two appendices at the end recall the basic results of Riemannian (resp.
    [Show full text]
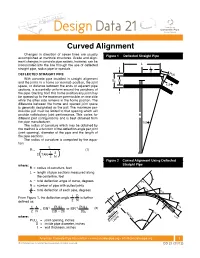
  • Design Data 21
    Design Data 21 Curved Alignment Changes in direction of sewer lines are usually Figure 1 Deflected Straight Pipe accomplished at manhole structures. Grade and align- Figure 1 Deflected Straight Pipe ment changes in concrete pipe sewers, however, can be incorporated into the line through the use of deflected L straight pipe, radius pipe or specials. t L 2 DEFLECTED STRAIGHT PIPE Pull With concrete pipe installed in straight alignment Bc D and the joints in a home (or normal) position, the joint ∆ space, or distance between the ends of adjacent pipe 1/2 N sections, is essentially uniform around the periphery of the pipe. Starting from this home position any joint may t be opened up to the maximum permissible on one side while the other side remains in the home position. The difference between the home and opened joint space is generally designated as the pull. The maximum per- missible pull must be limited to that opening which will provide satisfactory joint performance. This varies for R different joint configurations and is best obtained from the pipe manufacturer. ∆ 1/2 N The radius of curvature which may be obtained by this method is a function of the deflection angle per joint (joint opening), diameter of the pipe and the length of the pipe sections. The radius of curvature is computed by the equa- tion: L R = (1) 1 ∆ 2 TAN ( 2 N ) Figure 2 Curved Alignment Using Deflected Figure 2 Curved Alignment Using Deflected where: Straight Pipe R = radius of curvature, feet Straight Pipe L = length of pipe sections measured along the centerline, feet ∆ ∆ = total deflection angle of curve, degrees P.I.
    [Show full text]
  • AN INTRODUCTION to the CURVATURE of SURFACES by PHILIP ANTHONY BARILE a Thesis Submitted to the Graduate School-Camden Rutgers
    AN INTRODUCTION TO THE CURVATURE OF SURFACES By PHILIP ANTHONY BARILE A thesis submitted to the Graduate School-Camden Rutgers, The State University Of New Jersey in partial fulfillment of the requirements for the degree of Master of Science Graduate Program in Mathematics written under the direction of Haydee Herrera and approved by Camden, NJ January 2009 ABSTRACT OF THE THESIS An Introduction to the Curvature of Surfaces by PHILIP ANTHONY BARILE Thesis Director: Haydee Herrera Curvature is fundamental to the study of differential geometry. It describes different geometrical and topological properties of a surface in R3. Two types of curvature are discussed in this paper: intrinsic and extrinsic. Numerous examples are given which motivate definitions, properties and theorems concerning curvature. ii 1 1 Introduction For surfaces in R3, there are several different ways to measure curvature. Some curvature, like normal curvature, has the property such that it depends on how we embed the surface in R3. Normal curvature is extrinsic; that is, it could not be measured by being on the surface. On the other hand, another measurement of curvature, namely Gauss curvature, does not depend on how we embed the surface in R3. Gauss curvature is intrinsic; that is, it can be measured from on the surface. In order to engage in a discussion about curvature of surfaces, we must introduce some important concepts such as regular surfaces, the tangent plane, the first and second fundamental form, and the Gauss Map. Sections 2,3 and 4 introduce these preliminaries, however, their importance should not be understated as they lay the groundwork for more subtle and advanced topics in differential geometry.
    [Show full text]
  • Radius-Of-Curvature.Pdf
    CHAPTER 5 CURVATURE AND RADIUS OF CURVATURE 5.1 Introduction: Curvature is a numerical measure of bending of the curve. At a particular point on the curve , a tangent can be drawn. Let this line makes an angle Ψ with positive x- axis. Then curvature is defined as the magnitude of rate of change of Ψ with respect to the arc length s. Ψ Curvature at P = It is obvious that smaller circle bends more sharply than larger circle and thus smaller circle has a larger curvature. Radius of curvature is the reciprocal of curvature and it is denoted by ρ. 5.2 Radius of curvature of Cartesian curve: ρ = = (When tangent is parallel to x – axis) ρ = (When tangent is parallel to y – axis) Radius of curvature of parametric curve: ρ = , where and – Example 1 Find the radius of curvature at any pt of the cycloid , – Solution: Page | 1 – and Now ρ = = – = = =2 Example 2 Show that the radius of curvature at any point of the curve ( x = a cos3 , y = a sin3 ) is equal to three times the lenth of the perpendicular from the origin to the tangent. Solution : – – – = – 3a [–2 cos + ] 2 3 = 6 a cos sin – 3a cos = Now = – = Page | 2 = – – = – – = = 3a sin …….(1) The equation of the tangent at any point on the curve is 3 3 y – a sin = – tan (x – a cos ) x sin + y cos – a sin cos = 0 ……..(2) The length of the perpendicular from the origin to the tangent (2) is – p = = a sin cos ……..(3) Hence from (1) & (3), = 3p Example 3 If & ' are the radii of curvature at the extremities of two conjugate diameters of the ellipse = 1 prove that Solution: Parametric equation of the ellipse is x = a cos , y=b sin = – a sin , = b cos = – a cos , = – b sin The radius of curvature at any point of the ellipse is given by = = – – – – – Page | 3 = ……(1) For the radius of curvature at the extremity of other conjugate diameter is obtained by replacing by + in (1).
    [Show full text]
  • J.M. Sullivan, TU Berlin A: Curves Diff Geom I, SS 2015 This Course Is an Introduction to the Geometry of Smooth Curves and Surf
    J.M. Sullivan, TU Berlin A: Curves Diff Geom I, SS 2015 This course is an introduction to the geometry of smooth The length of an arbitrary curve can be defined (Jordan) as curves and surfaces in Euclidean space (usually R3). The lo- total variation: cal shape of a curve or surface is described in terms of its Xn curvatures. Many of the big theorems in the subject – such len(α) = TV(α) = sup α(ti) − α(ti−1) . as the Gauss–Bonnet theorem, a highlight at the end of the ··· ∈ t0< <tn I i=1 semester – deal with integrals of curvature. Some of these in- tegrals are topological constants, unchanged under deforma- This is the supremal length of inscribed polygons. (One can tion of the original curve or surface. show this length is finite over finite intervals if and only if α Usually not as level sets (like x2 + y2 = 1) as in algebraic has a Lipschitz reparametrization (e.g., by arclength). Lips- geometry, but parametrized (like (cos t, sin t)). chitz curves have velocity defined a.e., and our integral for- Of course, by Euclidean space [DE: euklidischer Raum] we mulas for length work fine.) n mean the vector space R 3 x = (x1,..., xn) with the stan- If J is another interval and ϕ: J → I is an orientation- dard scalar product [DE: Skalarprodukt] (also called an in- preserving homeomorphism, i.e., a strictly increasing surjec- P n ner product√ ) ha, bi = a · b = aibi and its associated norm tion, then α◦ϕ: J → R is a parametrized curve with the same |a| = ha, ai).
    [Show full text]