DOCSLIB.ORG

Heat Cycles, Heat Engines, & Real Devices

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Heat Cycles, Heat Engines, & Real Devices Heat Cycles, Heat Engines, & Real Devices John Jechura – [email protected] Updated: January 4, 2015 Topics • Heat engines / heat cycles . Review of ideal‐gas efficiency equations . Efficiency upper limit –Carnot Cycle • Water as working fluid in Rankine Cycle . Role of rotating equipment inefficiency • Advanced heat cycles . Reheat & heat recycle • Organic Rankine Cycle • Real devices . Gas & steam turbines 2 Heat Engines / Heat Cycles • Carnot cycle . Most efficient heat cycle possible Hot Reservoir @ T H • Rankine cycle Q H . Usually uses water (steam) as working fluid W . Creates the majority of electric power used net throughout the world Q C . Can use any heat source, including solar thermal, Cold Sink @ T coal, biomass, & nuclear C • Otto cycle . Approximates the pressure & volume of the combustion chamber of a spark‐ignited engine WQQ • Diesel cycle net H C th QQ . Approximates the pressure & volume of the HH combustion chamber of the Diesel engine 3 Carnot Cycle • Most efficient heat cycle possible • Steps . Reversible isothermal expansion of gas at TH. Combination of heat absorbed from hot reservoir & work done on the surroundings. Reversible isentropic & adiabatic expansion of the gas to TC. No heat transferred & work done on the surroundings. Reversible isothermal compression of gas at TC. Combination of heat released to cold sink & work done on the gas by the surroundings. Reversible isentropic & adiabatic compression of the gas to TH. No heat transferred & work done on the gas by the surroundings. • Thermal efficiency QQHC TT HC T C th th 1 QTTHHH 4 Rankine/Brayton Cycle • Different application depending on working fluid . Rankine cycle to describe closed steam cycle. Brayton cycle approximates gas turbine operation. • Steps . Heat at constant PH. Heat absorbed from hot reservoir & no work done. Isentropic & adiabatic expansion to PL. Work done on surroundings. Cool at constant PL. Heat released to cold sink & no work done. Isentropic & adiabatic compression to PH. Work done on fluid by surroundings. • Ideal gas thermal efficiency –not appropriate for condensing water 1/ TPLL th 11 TPHH 5 Thermal Efficiency Ideal‐Gas Brayton Cycle 0.8 Argon, =1.7 0.7 Air, =1.4 0.6 ) ( 0.5 0.4 Efficiency 0.3 Propane, =1.1 Thermal 0.2 0.1 0 0 5 10 15 20 25 30 35 Compression Ratio (P2/P1) 6 Otto Cycle • Steps . Reversible isentropic compression from V1 to V2. No heat transferred & work done on the fluid. Initial conditions are TL & PL. Heat at constant volume. Heat absorbed from hot reservoir & no work done. Reversible isentropic & adiabatic expansion from V2 to V1. No heat transferred & work done by the fluid on the surroundings. Cool at constant volume to TL with resulting pressure PL. Heat released to cold sink & no work done. • Thermal efficiency –ideal gas 1 1 where RV /V is the volumetric compression ratio th R1 12 • This cycle ignores input of new air/fuel mixture, change in composition with combustion, & exhaust of combustion products 7 Thermal Efficiency Ideal‐Gas Otto Cycle 60% 600 Inlet Conditions: 25°C & 1.0 bar =1.3 (typical air+fuel) 50% 500 40% 400 30% 300 Temperature [°C] Temperature Thermal Efficiency Thermal 20% 200 10% 100 0% 0 0 5 10 15 20 25 Volumetric Compression Ratio 8 Diesel Cycle • Steps . Reversible isentropic compression from V1 to V2. No heat transferred & work done on the fluid. Initial conditions are TL & PL. Heat at constant pressure. Heat absorbed from hot reservoir & no work done. Volume increases from V2 to V3. Reversible isentropic & adiabatic expansion from V3 to V1. No heat transferred & work done by the fluid on the surroundings. Cool at constant volume to TL with resulting pressure PL. Heat released to cold sink & no work done. • Thermal efficiency –ideal gas 11 1 th 1 R 1 where R=V1/V2 (the compression ratio) & =V3/V2 (the cut‐off ratio). • This cycle ignores input of new air, injection of fuel, change in composition with combustion, & exhaust of combustion products 9 Thermal Efficiency Ideal‐Gas Diesel Cycle 80% 800 Inlet Conditions: 25°C & 1.0 bar =1.4 (air) 70% =3.0 700 60% 600 50% 500 40% 400 30% 300 [°C] Temperature Thermal Efficiency Thermal 20% 200 10% 100 0% 0 0 5 10 15 20 25 Volumetric Compression Ratio 10 Example: Actual Gasoline Engine Thermal Efficiency • BMW M54B30 (2,979 cc) engine stated to produce 228 hp @ 5900 rpm (with 10.2:1 compression ratio) • Calculation steps to determine thermal efficiency . Unit conversion: 228 hp = 10,200 kJ/min 1.729 kJ/rev . 2 revolutions needed for full volume displacement: 1.161 kJ/L . Air+fuel mix has LHV of 3.511 kJ/L (ideal gas) • Assumptions o Characterize air as 21 mol% O2 / 79 mol% N2 & gasoline as isooctane (iC8, C8H18, LHV of 5065 kJ/mol) o Air+fuel mix an ideal‐gas stoichiometric mixture of @ 1.0 bar & 25°C o Air+fuel mix molar density is 0.0403 mol/L (i.g.) with 1.72 mol% iC8 • Thermal efficiency is 33% at these stated conditions . Ideal‐gas Otto Cycle shows upper limit of 50.2% (=1.3) 11 Gasoline Thermal Efficiency Using Aspen Plus 25 1 100 0.00 B1 7 HEATVAL FUEL 1 HIERARCHY 6052 FUELMIX 1.00 B2 W W-12 25 384 2674 1 24 116 5952 6052 6487 1.00 1.00 1.00 BURN-1 FLAMEVAL AIR MIX-HP 2A CMBSTGAS HIERARCHY B4 W Temperature (C) W-34 Pressure (bar) 1544 25 Molar Flow Rate (kmol/hr) Q-RESID 7 1 6487 6487 Vapor Fraction Q 1.00 0.89 Duty (kJ/sec) Power(kW) LOSTHEAT EXHAUST AMBIENT • 44.7% thermal efficiency assuming isentropic compression & expansion . Care must be taken to calculate heats & works from internal energy values, not enthalpy values . iC8 as model gasoline component . 10:1 volumetric compression ratio . 33% thermal efficiency & 33% lost heat to exhaust using 89% isentropic efficiency & 5% mechanical losses during compression & expansion 12 Water as Working Fluid in Rankine Cycle • Aspen Plus flowsheet . Flow system • Energy considerations from enthalpy, not internal energy . Cycle represented by once‐through flow system • LP‐WATER must match conditions of LP‐ WATR2 • “Out” direction of Energy & Work streams represent calculated values • Can use arbitrary flow rate for thermal efficiency calculation . Thermal efficiency from heat & work values Wnet W‐TURBIN W‐PUMP th Qin Q‐BOILER 13 Typical operating parameters • TURBINE exhaust fully condensed in CONDSR • BOILER increases temperature & changes phase . Outlet saturated liquid (i.e., vapor fraction is zero) or (liquid vapor) subcooled . At minimum, exit at saturated vapor conditions (i.e., • No vapor to PUMP to prevent cavitation vapor fraction is one). Temperature controlled by available cooling media . May be superheated to much higher temperature. • 15 –35oC (60 –95oF) typical for cooling water . Exit temperature controlled by heat source available & materials of construction –maximum about 420 – • 45 –50oC (110 – 125oF) typical for air cooling 580oC (790 – 1075oF) . Pressure will “float” to match this saturation • Highest temperatures require expensive nickel & temperature cobalt alloys • PUMP increases pressure of water to high‐ • Shaft work produced in TURBINE when pressure of pressure conditions steam let down to CONDSR inlet conditions . Pressure chosen to match common TURBINE inlet . Very complicated rotating machinery that can have pressures – 1500, 1800, & 2400 psig for large power multiple number of stages, multiple entry & applications extraction points, … . Real isentropic efficiencies 75 – 90% at optimal . Real isentropic efficiencies 70 – 90% at optimal flowrates flowrates • Inefficiency causes temperature rise in water . May be designed to exhaust gas phase or water/steam phase (condensing turbine) . Mechanical efficiency represents energy loss in drive train . Mechanical efficiency represents energy loss in drive train 14 Example #1 Steam Turbine Operation • Operating conditions . Condenser outlet saturated liquid @ 35oC • No pressure loss through exchanger . Pump outlet 1500 psig • Ideal compression . Boiler outlet saturated vapor • No pressure loss through exchanger . Turbine • Ideal expansion . No pressure losses through piping . No mechanical losses in rotating equipment W‐TURBIN W‐PUMP 2789 29 0.388 th Q‐BOILER 7111 15 Example #2 Steam Turbine Operation • Operating conditions . Condenser outlet saturated liquid @ 35oC • No pressure loss through exchanger . Pump outlet 1500 psig • 80% isentropic efficiency . Boiler outlet saturated vapor • No pressure loss through exchanger . Turbine • 75% isentropic efficiency . No pressure losses through piping . No mechanical losses in rotating equipment W‐TURBIN W‐PUMP 2092 36 0.289 th Q‐BOILER 7104 16 Advanced Heat Cycles • Reheat . Multiple step expansion, turbine exhaust reheated before next step . Keep the steam gas‐phase for as much of the process as possible . Increased thermal efficiency with increased capital cost • Heat recycle . Multiple step expansion, turbine exhaust split before next step • Majority sent to low‐pressure turbine • Remainder condensed against the high‐pressure boiler feed water . Trades off the heat of vaporization relative to power from expansion process 17 Example Steam Turbine With Reheat • Operating conditions . Condenser outlet saturated liquid @ 45oC • No pressure loss through exchanger . Pump outlet 120 bar‐a • Ideal compression . Boiler outlet 150oC superheat • No pressure loss through exchanger . Turbine intermediate 24 bar • 80% isentropic efficiency . Reheat to 475oC • No pressure loss through exchanger . No pressure losses through piping . No mechanical losses in rotating equipment 921 2465 34 th 0.341 8555 1277 18 Example Steam Turbine With Reheat 19 Example Steam Turbine With Heat Recycle • Operating conditions . Condenser outlet saturated liquid @ 45oC • No pressure loss through exchanger . Pump outlet 120 bar‐a • Ideal compression . Boiler outlet 150oC superheat • No pressure loss through exchanger . Turbine intermediate 10 bar • 80% isentropic efficiency . 10% split to recycle . No pressure losses through piping . No mechanical losses in rotating equipment 1306 1414 34 0.336 th 7986 20 Example Steam Turbine With Heat Recycle 21.
Load more

Recommended publications
  • Constant Volume Combustion Cycle for IC Engines
    Constant Volume Combustion Cycle for IC Engines Jovan Dorić Assistant This paper presents an analysis of the internal combustion engine cycle in University of Novi Sad Faculty of Technical Sciences cases when the new unconventional piston motion law is used. The main goal of the presented unconventional piston motion law is to make a Ivan Klinar realization of combustion during constant volume in an engine’s cylinder. Full Professor The obtained results are shown in PV (pressure-volume) diagrams of University of Novi Sad Faculty of Technical Sciences standard and new engine cycles. The emphasis is placed on the shortcomings of the real cycle in IC engines as well as policies that would Marko Dorić contribute to reducing these disadvantages. For this paper, volumetric PhD student efficiency, pressure and temperature curves for standard and new piston University of Novi Sad Faculty of Agriculture motion law have been calculated. Also, the results of improved efficiency and power are presented. Keywords: constant volume combustion, IC engine, kinematics. 1. INTRODUCTION of an internal combustion engine, whose combustion is so rapid that the piston does not move during the Internal combustion engine simulation modelling has combustion process, and thus combustion is assumed to long been established as an effective tool for studying take place at constant volume [6]. Although in engine performance and contributing to evaluation and theoretical terms heat addition takes place at constant new developments. Thermodynamic models of the real volume, in real engine cycle heat addition at constant engine cycle have served as effective tools for complete volume can not be performed.
    [Show full text]
  • Hybrid Electric Vehicles: a Review of Existing Configurations and Thermodynamic Cycles
    Review Hybrid Electric Vehicles: A Review of Existing Configurations and Thermodynamic Cycles Rogelio León , Christian Montaleza , José Luis Maldonado , Marcos Tostado-Véliz * and Francisco Jurado Department of Electrical Engineering, University of Jaén, EPS Linares, 23700 Jaén, Spain; [email protected] (R.L.); [email protected] (C.M.); [email protected] (J.L.M.); [email protected] (F.J.) * Correspondence: [email protected]; Tel.: +34-953-648580 Abstract: The mobility industry has experienced a fast evolution towards electric-based transport in recent years. Recently, hybrid electric vehicles, which combine electric and conventional combustion systems, have become the most popular alternative by far. This is due to longer autonomy and more extended refueling networks in comparison with the recharging points system, which is still quite limited in some countries. This paper aims to conduct a literature review on thermodynamic models of heat engines used in hybrid electric vehicles and their respective configurations for series, parallel and mixed powertrain. It will discuss the most important models of thermal energy in combustion engines such as the Otto, Atkinson and Miller cycles which are widely used in commercial hybrid electric vehicle models. In short, this work aims at serving as an illustrative but descriptive document, which may be valuable for multiple research and academic purposes. Keywords: hybrid electric vehicle; ignition engines; thermodynamic models; autonomy; hybrid configuration series-parallel-mixed; hybridization; micro-hybrid; mild-hybrid; full-hybrid Citation: León, R.; Montaleza, C.; Maldonado, J.L.; Tostado-Véliz, M.; Jurado, F. Hybrid Electric Vehicles: A Review of Existing Configurations 1. Introduction and Thermodynamic Cycles.
    [Show full text]
  • Generation of Entropy in Spark Ignition Engines
    Int. J. of Thermodynamics ISSN 1301-9724 Vol. 10 (No. 2), pp. 53-60, June 2007 Generation of Entropy in Spark Ignition Engines Bernardo Ribeiro, Jorge Martins*, António Nunes Universidade do Minho, Departamento de Engenharia Mecânica 4800-058 Guimarães PORTUGAL [email protected] Abstract Recent engine development has focused mainly on the improvement of engine efficiency and output emissions. The improvements in efficiency are being made by friction reduction, combustion improvement and thermodynamic cycle modification. New technologies such as Variable Valve Timing (VVT) or Variable Compression Ratio (VCR) are important for the latter. To assess the improvement capability of engine modifications, thermodynamic analysis of indicated cycles of the engines is made using the first and second laws of thermodynamics. The Entropy Generation Minimization (EGM) method proposes the identification of entropy generation sources and the reduction of the entropy generated by those sources as a method to improve the thermodynamic performance of heat engines and other devices. A computer model created and implemented in MATLAB Simulink was used to simulate the conventional Otto cycle and the various processes (combustion, free expansion during exhaust, heat transfer and fluid flow through valves and throttle) were evaluated in terms of the amount of the entropy generated. An Otto cycle, a Miller cycle (over-expanded cycle) and a Miller cycle with compression ratio adjustment are studied using the referred model in order to evaluate the amount of entropy generated in each cycle. All cycles are compared in terms of work produced per cycle. Keywords: IC engines, Miller cycle, entropy generation, over-expanded cycle 1.
    [Show full text]
  • Thermodynamics of Power Generation
    THERMAL MACHINES AND HEAT ENGINES Thermal machines ......................................................................................................................................... 1 The heat engine ......................................................................................................................................... 2 What it is ............................................................................................................................................... 2 What it is for ......................................................................................................................................... 2 Thermal aspects of heat engines ........................................................................................................... 3 Carnot cycle .............................................................................................................................................. 3 Gas power cycles ...................................................................................................................................... 4 Otto cycle .............................................................................................................................................. 5 Diesel cycle ........................................................................................................................................... 8 Brayton cycle .....................................................................................................................................
    [Show full text]
  • An Analytic Study of Applying Miller Cycle to Reduce Nox Emission from Petrol Engine Yaodong Wang, Lin Lin, Antony P
    An analytic study of applying miller cycle to reduce nox emission from petrol engine Yaodong Wang, Lin Lin, Antony P. Roskilly, Shengchuo Zeng, Jincheng Huang, Yunxin He, Xiaodong Huang, Huilan Huang, Haiyan Wei, Shangping Li, et al. To cite this version: Yaodong Wang, Lin Lin, Antony P. Roskilly, Shengchuo Zeng, Jincheng Huang, et al.. An analytic study of applying miller cycle to reduce nox emission from petrol engine. Applied Thermal Engineering, Elsevier, 2007, 27 (11-12), pp.1779. 10.1016/j.applthermaleng.2007.01.013. hal-00498945 HAL Id: hal-00498945 https://hal.archives-ouvertes.fr/hal-00498945 Submitted on 9 Jul 2010 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Accepted Manuscript An analytic study of applying miller cycle to reduce nox emission from petrol engine Yaodong Wang, Lin Lin, Antony P. Roskilly, Shengchuo Zeng, Jincheng Huang, Yunxin He, Xiaodong Huang, Huilan Huang, Haiyan Wei, Shangping Li, J Yang PII: S1359-4311(07)00031-2 DOI: 10.1016/j.applthermaleng.2007.01.013 Reference: ATE 2070 To appear in: Applied Thermal Engineering Received Date: 5 May 2006 Revised Date: 2 January 2007 Accepted Date: 14 January 2007 Please cite this article as: Y.
    [Show full text]
  • 3.5 the Internal Combustion Engine (Otto Cycle)
    Thermodynamics and Propulsion Next: 3.6 Diesel Cycle Up: 3. The First Law Previous: 3.4 Refrigerators and Heat Contents Index Subsections 3.5.1 Efficiency of an ideal Otto cycle 3.5.2 Engine work, rate of work per unit enthalpy flux 3.5 The Internal combustion engine (Otto Cycle) [VW, S & B: 9.13] The Otto cycle is a set of processes used by spark ignition internal combustion engines (2-stroke or 4- stroke cycles). These engines a) ingest a mixture of fuel and air, b) compress it, c) cause it to react, thus effectively adding heat through converting chemical energy into thermal energy, d) expand the combustion products, and then e) eject the combustion products and replace them with a new charge of fuel and air. The different processes are shown in Figure 3.8: 1. Intake stroke, gasoline vapor and air drawn into engine ( ). 2. Compression stroke, , increase ( ). 3. Combustion (spark), short time, essentially constant volume ( ). Model: heat absorbed from a series of reservoirs at temperatures to . 4. Power stroke: expansion ( ). 5. Valve exhaust: valve opens, gas escapes. 6. ( ) Model: rejection of heat to series of reservoirs at temperatures to . 7. Exhaust stroke, piston pushes remaining combustion products out of chamber ( ). We model the processes as all acting on a fixed mass of air contained in a piston-cylinder arrangement, as shown in Figure 3.10. Figure 3.8: The ideal Otto cycle Figure 3.9: Sketch of an actual Otto cycle Figure 3.10: Piston and valves in a four-stroke internal combustion engine The actual cycle does not have the sharp transitions between the different processes that the ideal cycle has, and might be as sketched in Figure 3.9.
    [Show full text]
  • Performance Analysis of a Diesel Cycle Under the Restriction of Maximum Cycle Temperature with Considerations of Heat Loss, Friction, and Variable Specific Heats S.S
    Vol. 120 (2011) ACTA PHYSICA POLONICA A No. 6 Performance Analysis of a Diesel Cycle under the Restriction of Maximum Cycle Temperature with Considerations of Heat Loss, Friction, and Variable Specific Heats S.S. Houa;¤ and J.C. Linb aDepartment of Mechanical Engineering, Kun Shan University, Tainan City 71003, Taiwan, ROC bDepartment of General Education, Transworld University, Touliu City, Yunlin County 640, Taiwan, ROC (Received November 11, 2010) The objective of this study is to examine the influences of heat loss characterized by a percentage of fuel’s energy, friction and variable specific heats of working fluid on the performance of an air standard Diesel cycle with the restriction of maximum cycle temperature. A more realistic and precise relationship between the fuel’s chemical energy and the heat leakage that is constituted on a pair of inequalities is derived through the resulting temperature. The variations in power output and thermal efficiency with compression ratio, and the relations between the power output and the thermal efficiency of the cycle are presented. The results show that the power output as well as the efficiency where maximum power output occurs will increase with the increase of maximum cycle temperature. The temperature-dependent specific heats of working fluid have a significant influence on the performance. The power output and the working range of the cycle increase while the efficiency decreases with increasing specific heats of working fluid. The friction loss has a negative effect on the performance. Therefore, the power output and efficiency of the cycle decrease with increasing friction loss. It is noteworthy that the effects of heat loss characterized by a percentage of fuel’s energy, friction and variable specific heats of working fluid on the performance of a Diesel-cycle engine are significant and should be considered in practice cycle analysis.
    [Show full text]
  • Air Standard Assumptions Some Definitions for Reciprocation Engines
    Air Standard Assumptions In power engines, energy is provided by burning fuel within the system boundaries, i.e., internal combustion engines. The following assumptions are commonly known as the air- standard assumptions: 1- The working fluid is air, which continuously circulates in a closed loop (cycle). Air is considered as ideal gas. 2- All the processes in (ideal) power cycles are internally reversible. 3- Combustion process is modeled by a heat-addition process from an external source. 4- The exhaust process is modeled by a heat-rejection process that restores the working fluid (air) at its initial state. Assuming constant specific heats, (@25°C) for air, is called cold-air-standard assumption. Some Definitions for Reciprocation Engines: The reciprocation engine is one the most common machines that is being used in a wide variety of applications from automobiles to aircrafts to ships, etc. Intake Exhaust valve valve TDC Bore Stroke BDC Fig. 3-1: Reciprocation engine. Top dead center (TDC): The position of the piston when it forms the smallest volume in the cylinder. Bottom dead center (BDC): The position of the piston when it forms the largest volume in the cylinder. Stroke: The largest distance that piston travels in one direction. Bore: The diameter of the piston. M. Bahrami ENSC 461 (S 11) IC Engines 1 Clearance volume: The minimum volume formed in the cylinder when the piston is at TDC. Displacement volume: The volume displaced by the piston as it moves between the TDC and BDC. Compression ratio: The ratio of maximum to minimum (clearance) volumes in the cylinder: V V r max BDC Vmin VTDC Mean effective pressure (MEP): A fictitious (constant throughout the cycle) pressure that if acted on the piston will produce the work.
    [Show full text]
  • Performance Study for Miller Cycle Natural Gas Engine Based on GT-Power
    Journal of Clean Energy Technologies, Vol. 3, No. 5, September 2015 Performance Study for Miller Cycle Natural Gas Engine Based on GT-Power Songsong Song and Hongguang Zhang [4]. Abstract—In order to improve the thermal efficiency of However, few attentions have been paid to the working natural gas engine and reduce the NOx emission from engine, process of the natural gas engine. In this paper, GT-Power this paper presented the technical route which applied Miller software was used to simulate the turbocharged natural gas cycle to turbocharged lean-burn natural gas engine. GT-Power engine. BSFC and NO emission were analyzed for two software was used to model the turbocharged natural gas x engine, and simulation research based on Miller cycle was kinds of engine working processes based on Otto cycle and performed according to various engine loads in the engine Miller cycle respectively. speed range of 2000-5000rpm. The simulation results showed that, under part load (50% of the engine full load) operating conditions of the turbocharged lean-burn natural gas engine, II. METHODOLOGY compared with Otto cycle, Miller cycle can reduce the brake specific fuel consumption (BSFC) and NOx emission. Under In order to improve the thermal efficiency of the engine, high load and low speed as well as moderate load and high Ralph Miller proposed Miller cycle in 1947 [5], which is a speed operating conditions, Miller cycle can effectively reduce kind of over-expanded cycle, as shown in Fig. 1. the BSFC. Under high load and low speed or high speed operating conditions, the NOx emission can be reduced apparently.
    [Show full text]
  • Power Plant 3
    Centre of Excellence in Renewable Energy Education and Research, New Campus, University of Lucknow, Lucknow B Voc. Renewable Energy Technology Semester II First Year Module RET-203: Power Plant Engineering Unit-2 (Air Standard cycle and Diesel Electric Power Plant) Contents: Internal Combustion Engine and External Combustion Engine: Otto Cycle, Diesel Cycle, Dual Cycle, Efficiency and Indicator Diagram. Diesel Electric Power Plant: Working Principle, Layout, Performance and Thermal Efficiency, Combined Cycle Power Plant, Layout, Efficiency. Internal Combustion Engine and External Combustion Engine In an external combustion engine, the fuel isn't burned inside the engine. With an internal combustion engine, the combustion chamber lies right in the middle of the engine. An Internal combustion engines rely on the explosive power of the fuel within the engine to produce work. In internal combustion engines, the explosion forcefully pushes pistons or expels hot high-pressure gas out of the engine at great speeds. Both moving pistons and ejected high- speed gas have the ability to do work. In external combustion engines, combustion heats a fluid which, in turn, does all the work. Example: Atkinson, Brayton/Joule, Diesel, Otto, Gas Generator etc. An external combustion engine uses a working fluid, either a liquid or a gas or both, that is heated by a fuel burned outside the engine. The external combustion chamber is filled with a fuel and air mixture that is ignited to produce a large amount of heat. This heat is then used to heat the internal working fluid either through the engine wall or a heat exchanger. The fluid expands when heated, acting on the mechanism of the engine, thus producing motion and usable work.
    [Show full text]
  • Efficiency at Maximum Power of the Low-Dissipation Hybrid
    energies Article Efficiency at Maximum Power of the Low-Dissipation Hybrid Electrochemical–Otto Cycle David Diskin 1 and Leonid Tartakovsky 1,2,* 1 Faculty of Mechanical Engineering, Technion—Israel Institute of Technology, Haifa 3200003, Israel; [email protected] 2 Grand Technion Energy Program, Technion—Israel Institute of Technology, Haifa 3200003, Israel * Correspondence: [email protected] Received: 24 June 2020; Accepted: 24 July 2020; Published: 1 August 2020 Abstract: A novel analytical method was developed for analysis of efficiency at maximum power of a hybrid cycle combining electrochemical and Otto engines. The analysis is based on the low-dissipation model, which relates energy dissipation with energy transfer rate. Efficiency at maximum power of a hybrid engine operating between two reservoirs of chemical potentials is evaluated. The engine is composed of an electrochemical device that transforms chemical potential to electrical work of an Otto engine that uses the heat generated in the electrochemical device and its exhaust effluent for mechanical work production. The results show that efficiency at maximum power of the hybrid cycle is identical to the efficiency at maximum power of an electrochemical engine alone; however, the power is the product of the electrochemical engine power and the compression ratio of the Otto engine. Partial mass transition by the electrochemical device from the high to the low chemical potential is also examined. In the latter case, heat is generated both in the electrochemical device and the Otto engine, and the efficiency at maximum power is a function of the compression ratio. An analysis performed using the developed method shows, for the first time, that, in terms of a maximal power, at some conditions, Otto cycle can provide better performance that the hybrid cycle.
    [Show full text]
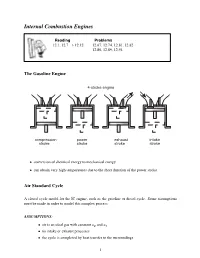
  • Internal Combustion Engines
    Internal Combustion Engines Reading Problems 12.1, 12.7 ! 12.12 12.67, 12.74, 12.81, 12.82 12.86, 12.89, 12.94 The Gasoline Engine • conversion of chemical energy to mechanical energy • can obtain very high temperatures due to the short duration of the power stroke Air Standard Cycle A closed cycle model for the IC engine, such as the gasoline or diesel cycle. Some assumptions must be made in order to model this complex process. ASSUMPTIONS: • air is an ideal gas with constant cp and cv • no intake or exhaust processes • the cycle is completed by heat transfer to the surroundings 1 • the internal combustion process is replaced by a heat transfer process from a TER • all internal processes are reversible • heat addition occurs instantaneously while the piston is at TDC Definitions Mean Effective Pressure (MEP): The theoretical constant pressure that, if it acted on the piston during the power stroke would produce the same net work as actually developed in one complete cycle. net work for one cycle W MEP = = net displacement volume VBDC − VT DC The mean effective pressure is an index that relates the work output of the engine to it size (displacement volume). Otto Cycle • the theoretical model for the gasoline engine • consists of four internally reversible processes • heat is transferred to the working fluid at constant volume Otto Cycle Efficiency W Q − Q Q Q η = net = H L = 1 − L = 1 − 4−1 QH QH QH Q2−3 QH = mcv(T3 − T2)(intake) QL = mcv(T4 − T1)(exhaust) Therefore ! T4 ! − 1 (T4 − T1) T1 T1 η = 1 − = 1 − ! (T − T ) T T3 3 2 2 − 1 T2 2 Since
    [Show full text]