Multiple Data Splitting for Testing
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Applied Biostatistics Mean and Standard Deviation the Mean the Median Is Not the Only Measure of Central Value for a Distribution
Health Sciences M.Sc. Programme Applied Biostatistics Mean and Standard Deviation The mean The median is not the only measure of central value for a distribution. Another is the arithmetic mean or average, usually referred to simply as the mean. This is found by taking the sum of the observations and dividing by their number. The mean is often denoted by a little bar over the symbol for the variable, e.g. x . The sample mean has much nicer mathematical properties than the median and is thus more useful for the comparison methods described later. The median is a very useful descriptive statistic, but not much used for other purposes. Median, mean and skewness The sum of the 57 FEV1s is 231.51 and hence the mean is 231.51/57 = 4.06. This is very close to the median, 4.1, so the median is within 1% of the mean. This is not so for the triglyceride data. The median triglyceride is 0.46 but the mean is 0.51, which is higher. The median is 10% away from the mean. If the distribution is symmetrical the sample mean and median will be about the same, but in a skew distribution they will not. If the distribution is skew to the right, as for serum triglyceride, the mean will be greater, if it is skew to the left the median will be greater. This is because the values in the tails affect the mean but not the median. Figure 1 shows the positions of the mean and median on the histogram of triglyceride. -

TR Multivariate Conditional Median Estimation
Discussion Paper: 2004/02 TR multivariate conditional median estimation Jan G. de Gooijer and Ali Gannoun www.fee.uva.nl/ke/UvA-Econometrics Department of Quantitative Economics Faculty of Economics and Econometrics Universiteit van Amsterdam Roetersstraat 11 1018 WB AMSTERDAM The Netherlands TR Multivariate Conditional Median Estimation Jan G. De Gooijer1 and Ali Gannoun2 1 Department of Quantitative Economics University of Amsterdam Roetersstraat 11, 1018 WB Amsterdam, The Netherlands Telephone: +31—20—525 4244; Fax: +31—20—525 4349 e-mail: [email protected] 2 Laboratoire de Probabilit´es et Statistique Universit´e Montpellier II Place Eug`ene Bataillon, 34095 Montpellier C´edex 5, France Telephone: +33-4-67-14-3578; Fax: +33-4-67-14-4974 e-mail: [email protected] Abstract An affine equivariant version of the nonparametric spatial conditional median (SCM) is con- structed, using an adaptive transformation-retransformation (TR) procedure. The relative performance of SCM estimates, computed with and without applying the TR—procedure, are compared through simulation. Also included is the vector of coordinate conditional, kernel- based, medians (VCCMs). The methodology is illustrated via an empirical data set. It is shown that the TR—SCM estimator is more efficient than the SCM estimator, even when the amount of contamination in the data set is as high as 25%. The TR—VCCM- and VCCM estimators lack efficiency, and consequently should not be used in practice. Key Words: Spatial conditional median; kernel; retransformation; robust; transformation. 1 Introduction p s Let (X1, Y 1),...,(Xn, Y n) be independent replicates of a random vector (X, Y ) IR IR { } ∈ × where p > 1,s > 2, and n>p+ s. -

5. the Student T Distribution
Virtual Laboratories > 4. Special Distributions > 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 5. The Student t Distribution In this section we will study a distribution that has special importance in statistics. In particular, this distribution will arise in the study of a standardized version of the sample mean when the underlying distribution is normal. The Probability Density Function Suppose that Z has the standard normal distribution, V has the chi-squared distribution with n degrees of freedom, and that Z and V are independent. Let Z T= √V/n In the following exercise, you will show that T has probability density function given by −(n +1) /2 Γ((n + 1) / 2) t2 f(t)= 1 + , t∈ℝ ( n ) √n π Γ(n / 2) 1. Show that T has the given probability density function by using the following steps. n a. Show first that the conditional distribution of T given V=v is normal with mean 0 a nd variance v . b. Use (a) to find the joint probability density function of (T,V). c. Integrate the joint probability density function in (b) with respect to v to find the probability density function of T. The distribution of T is known as the Student t distribution with n degree of freedom. The distribution is well defined for any n > 0, but in practice, only positive integer values of n are of interest. This distribution was first studied by William Gosset, who published under the pseudonym Student. In addition to supplying the proof, Exercise 1 provides a good way of thinking of the t distribution: the t distribution arises when the variance of a mean 0 normal distribution is randomized in a certain way. -

The Probability Lifesaver: Order Statistics and the Median Theorem
The Probability Lifesaver: Order Statistics and the Median Theorem Steven J. Miller December 30, 2015 Contents 1 Order Statistics and the Median Theorem 3 1.1 Definition of the Median 5 1.2 Order Statistics 10 1.3 Examples of Order Statistics 15 1.4 TheSampleDistributionoftheMedian 17 1.5 TechnicalboundsforproofofMedianTheorem 20 1.6 TheMedianofNormalRandomVariables 22 2 • Greetings again! In this supplemental chapter we develop the theory of order statistics in order to prove The Median Theorem. This is a beautiful result in its own, but also extremely important as a substitute for the Central Limit Theorem, and allows us to say non- trivial things when the CLT is unavailable. Chapter 1 Order Statistics and the Median Theorem The Central Limit Theorem is one of the gems of probability. It’s easy to use and its hypotheses are satisfied in a wealth of problems. Many courses build towards a proof of this beautiful and powerful result, as it truly is ‘central’ to the entire subject. Not to detract from the majesty of this wonderful result, however, what happens in those instances where it’s unavailable? For example, one of the key assumptions that must be met is that our random variables need to have finite higher moments, or at the very least a finite variance. What if we were to consider sums of Cauchy random variables? Is there anything we can say? This is not just a question of theoretical interest, of mathematicians generalizing for the sake of generalization. The following example from economics highlights why this chapter is more than just of theoretical interest. -
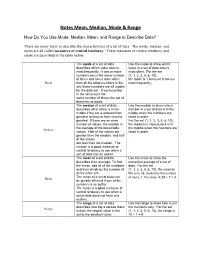
Notes Mean, Median, Mode & Range
Notes Mean, Median, Mode & Range How Do You Use Mode, Median, Mean, and Range to Describe Data? There are many ways to describe the characteristics of a set of data. The mode, median, and mean are all called measures of central tendency. These measures of central tendency and range are described in the table below. The mode of a set of data Use the mode to show which describes which value occurs value in a set of data occurs most frequently. If two or more most often. For the set numbers occur the same number {1, 1, 2, 3, 5, 6, 10}, of times and occur more often the mode is 1 because it occurs Mode than all the other numbers in the most frequently. set, those numbers are all modes for the data set. If each number in the set occurs the same number of times, the set of data has no mode. The median of a set of data Use the median to show which describes what value is in the number in a set of data is in the middle if the set is ordered from middle when the numbers are greatest to least or from least to listed in order. greatest. If there are an even For the set {1, 1, 2, 3, 5, 6, 10}, number of values, the median is the median is 3 because it is in the average of the two middle the middle when the numbers are Median values. Half of the values are listed in order. greater than the median, and half of the values are less than the median. -

Global Investigation of Return Autocorrelation and Its Determinants
Global investigation of return autocorrelation and its determinants Pawan Jaina,, Wenjun Xueb aUniversity of Wyoming bFlorida International University ABSTRACT We estimate global return autocorrelation by using the quantile autocorrelation model and investigate its determinants across 43 stock markets from 1980 to 2013. Although our results document a decline in autocorrelation across the entire sample period for all countries, return autocorrelation is significantly larger in emerging markets than in developed markets. The results further document that larger and liquid stock markets have lower return autocorrelation. We also find that price limits in most emerging markets result in higher return autocorrelation. We show that the disclosure requirement, public enforcement, investor psychology, and market characteristics significantly affect return autocorrelation. Our results document that investors from different cultural backgrounds and regulation regimes react differently to corporate disclosers, which affects return autocorrelation. Keywords: Return autocorrelation, Global stock markets, Quantile autoregression model, Legal environment, Investor psychology, Hofstede’s cultural dimensions JEL classification: G12, G14, G15 Corresponding author, E-mail: [email protected]; fax: 307-766-5090. 1. Introduction One of the most striking asset pricing anomalies is the existence of large, positive, short- horizon return autocorrelation in stock portfolios, first documented in Conrad and Kaul (1988) and Lo and MacKinlay (1990). This existence of -

Power Birnbaum-Saunders Student T Distribution
Revista Integración Escuela de Matemáticas Universidad Industrial de Santander H Vol. 35, No. 1, 2017, pág. 51–70 Power Birnbaum-Saunders Student t distribution Germán Moreno-Arenas a ∗, Guillermo Martínez-Flórez b Heleno Bolfarine c a Universidad Industrial de Santander, Escuela de Matemáticas, Bucaramanga, Colombia. b Universidad de Córdoba, Departamento de Matemáticas y Estadística, Montería, Colombia. c Universidade de São Paulo, Departamento de Estatística, São Paulo, Brazil. Abstract. The fatigue life distribution proposed by Birnbaum and Saunders has been used quite effectively to model times to failure for materials sub- ject to fatigue. In this article, we introduce an extension of the classical Birnbaum-Saunders distribution substituting the normal distribution by the power Student t distribution. The new distribution is more flexible than the classical Birnbaum-Saunders distribution in terms of asymmetry and kurto- sis. We discuss maximum likelihood estimation of the model parameters and associated regression model. Two real data set are analysed and the results reveal that the proposed model better some other models proposed in the literature. Keywords: Birnbaum-Saunders distribution, alpha-power distribution, power Student t distribution. MSC2010: 62-07, 62F10, 62J02, 62N86. Distribución Birnbaum-Saunders Potencia t de Student Resumen. La distribución de probabilidad propuesta por Birnbaum y Saun- ders se ha usado con bastante eficacia para modelar tiempos de falla de ma- teriales sujetos a la fátiga. En este artículo definimos una extensión de la distribución Birnbaum-Saunders clásica sustituyendo la distribución normal por la distribución potencia t de Student. La nueva distribución es más flexi- ble que la distribución Birnbaum-Saunders clásica en términos de asimetría y curtosis. -

Lectures on Statistics
Lectures on Statistics William G. Faris December 1, 2003 ii Contents 1 Expectation 1 1.1 Random variables and expectation . 1 1.2 The sample mean . 3 1.3 The sample variance . 4 1.4 The central limit theorem . 5 1.5 Joint distributions of random variables . 6 1.6 Problems . 7 2 Probability 9 2.1 Events and probability . 9 2.2 The sample proportion . 10 2.3 The central limit theorem . 11 2.4 Problems . 13 3 Estimation 15 3.1 Estimating means . 15 3.2 Two population means . 17 3.3 Estimating population proportions . 17 3.4 Two population proportions . 18 3.5 Supplement: Confidence intervals . 18 3.6 Problems . 19 4 Hypothesis testing 21 4.1 Null and alternative hypothesis . 21 4.2 Hypothesis on a mean . 21 4.3 Two means . 23 4.4 Hypothesis on a proportion . 23 4.5 Two proportions . 24 4.6 Independence . 24 4.7 Power . 25 4.8 Loss . 29 4.9 Supplement: P-values . 31 4.10 Problems . 33 iii iv CONTENTS 5 Order statistics 35 5.1 Sample median and population median . 35 5.2 Comparison of sample mean and sample median . 37 5.3 The Kolmogorov-Smirnov statistic . 38 5.4 Other goodness of fit statistics . 39 5.5 Comparison with a fitted distribution . 40 5.6 Supplement: Uniform order statistics . 41 5.7 Problems . 42 6 The bootstrap 43 6.1 Bootstrap samples . 43 6.2 The ideal bootstrap estimator . 44 6.3 The Monte Carlo bootstrap estimator . 44 6.4 Supplement: Sampling from a finite population . -

4. Descriptive Statistics
4. Descriptive statistics Any time that you get a new data set to look at one of the first tasks that you have to do is find ways of summarising the data in a compact, easily understood fashion. This is what descriptive statistics (as opposed to inferential statistics) is all about. In fact, to many people the term “statistics” is synonymous with descriptive statistics. It is this topic that we’ll consider in this chapter, but before going into any details, let’s take a moment to get a sense of why we need descriptive statistics. To do this, let’s open the aflsmall_margins file and see what variables are stored in the file. In fact, there is just one variable here, afl.margins. We’ll focus a bit on this variable in this chapter, so I’d better tell you what it is. Unlike most of the data sets in this book, this is actually real data, relating to the Australian Football League (AFL).1 The afl.margins variable contains the winning margin (number of points) for all 176 home and away games played during the 2010 season. This output doesn’t make it easy to get a sense of what the data are actually saying. Just “looking at the data” isn’t a terribly effective way of understanding data. In order to get some idea about what the data are actually saying we need to calculate some descriptive statistics (this chapter) and draw some nice pictures (Chapter 5). Since the descriptive statistics are the easier of the two topics I’ll start with those, but nevertheless I’ll show you a histogram of the afl.margins data since it should help you get a sense of what the data we’re trying to describe actually look like, see Figure 4.2. -

Multivariate Symmetry and Asymme- Try
MULTIVARIATE SYMMETRY AND ASYMME- TRY (By Robert Serfling, January 2003, for Encyclopedia of Statistical Sciences, 2nd ed.) Abstract. Univariate symmetry has interesting and diverse forms of generalization to the multivariate case. Here several leading concepts of multivariate symmetry — spherical, elliptical, central and angular — are examined and various closely related notions discussed. Methods for testing the hypothesis of symmetry, and approaches for measuring the direction and magnitude of skewness, are reviewed. Keywords and Phrases. Multivariate, Symmetry, Skewness, Asymmetry. AMS Subject Classification. Primary: 62H99; Secondary: 62G99 CONCEPTS OF SYMMETRY The idea of “symmetry” has served, from ancient times, as a conceptual reference point in art and mathematics and in their diverse applications. In aesthetics it is a principle of order, in mathematics an artifact of geometric structure, in philosophy an abstraction of balance and harmony and perfection, in poetry an intuitive essence of nature and divinity. Weyl [52] has created a delightful and wide-ranging treatment of “symmetry”, from bilateral symmetry in Greek sculpture to Kant’s metaphysical pondering of the problem of left and right to the description of cystalline structure in nature by modern group theory. Here we focus on the notion of symmetry as it relates to multivariate probability distributions in statistical science. Nevertheless even in this specialized context there are many variations on the theme. One can seek to define useful classes of distributions that extend the multivariate normal distribution. Or one can formulate multivariate generalizations of particular univariate distributions such as the exponential. One can define symmetry in terms of structural properties of the distribution function, or of the characteristic function, or of the density function. -

UNIT NUMBER 19.4 PROBABILITY 4 (Measures of Location and Dispersion)
“JUST THE MATHS” UNIT NUMBER 19.4 PROBABILITY 4 (Measures of location and dispersion) by A.J.Hobson 19.4.1 Common types of measure 19.4.2 Exercises 19.4.3 Answers to exercises UNIT 19.4 - PROBABILITY 4 MEASURES OF LOCATION AND DISPERSION 19.4.1 COMMON TYPES OF MEASURE We include, here three common measures of location (or central tendency), and one common measure of dispersion (or scatter), used in the discussion of probability distributions. (a) The Mean (i) For Discrete Random Variables If the values x1, x2, x3, . , xn of a discrete random variable, x, have probabilities P1,P2,P3,....,Pn, respectively, then Pi represents the expected frequency of xi divided by the total number of possible outcomes. For example, if the probability of a certain value of x is 0.25, then there is a one in four chance of its occurring. The arithmetic mean, µ, of the distribution may therefore be given by the formula n X µ = xiPi. i=1 (ii) For Continuous Random Variables In this case, it is necessary to use the probability density function, f(x), for the distribution which is the rate of increase of the probability distribution function, F (x). For a small interval, δx of x-values, the probability that any of these values occurs is ap- proximately f(x)δx, which leads to the formula Z ∞ µ = xf(x) dx. −∞ (b) The Median (i) For Discrete Random Variables The median provides an estimate of the middle value of x, taking into account the frequency at which each value occurs. -

Descriptive Statistics
Statistics: Descriptive Statistics When we are given a large data set, it is necessary to describe the data in some way. The raw data is just too large and meaningless on its own to make sense of. We will sue the following exam scores data throughout: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10 45, 67, 87, 21, 43, 98, 28, 23, 28, 75 Summary Statistics We can use the raw data to calculate summary statistics so that we have some idea what the data looks like and how sprad out it is. Max, Min and Range The maximum value of the dataset and the minimum value of the dataset are very simple measures. The range of the data is difference between the maximum and minimum value. Range = Max Value − Min Value = 98 − 21 = 77 Mean, Median and Mode The mean, median and mode are measures of central tendency of the data (i.e. where is the center of the data). Mean (µ) The mean is sum of all values divided by how many values there are N 1 X 45 + 67 + 87 + 21 + 43 + 98 + 28 + 23 + 28 + 75 xi = = 51.5 N i=1 10 Median The median is the middle data point when the dataset is arranged in order from smallest to largest. If there are two middle values then we take the average of the two values. Using the data above check that the median is: 44 Mode The mode is the value in the dataset that appears most. Using the data above check that the mode is: 28 Standard Deviation The standard deviation (σ) measures how spread out the data is.