DOCSLIB.ORG

Abundance of Atlantic Salmon in the Stewiacke River, NS, from 1965

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Abundance of Atlantic Salmon in the Stewiacke River, NS, from 1965 Bayesian Analysis of Extinction Risk in Atlantic Salmon A.J.F. Gibson1, P.G. Amiro1 and 2 R.A. Myers 1Department of Fisheries and Oceans, Dartmouth, NS 2Dalhousie University, Halifax, NS Overview • Endangered Species • Approach to Assessment • Questions - Needs • Inner Bay of Fundy Salmon • Index-based model of population size and trajectory • Summary: • Bayesian considerations for endangered species • Future work Species-at-Risk vs. Fisheries Modeling • The range of actions or activities to be evaluated are typically wider • habitat protection, creation or restoration, supportive rearing, bycatch reduction • Abundance is at levels where dynamics are less certain • potential Allee effects, demographic vs. environmental stochasticity • Populations are often data poor • Higher level of precision is sometimes required • unachievable • Dynamics have likely changed • implications for selection of priors Endangered Species: Challenges for Modelling • Challenges: • often data poor • life history often not well understood • Recovery planning has very specific requirements: • assessment of recovery potential, critical habitat designation, recovery targets • may require greater knowledge and model resolution than for exploited species • What is the role of Bayesian methods in this process? Species at Risk: Three Key Questions 1. What is the population’s current size and trajectory? • Risk, timeline for recovery 2. What are the differences in the past and the present population dynamics? • Which life history parameters changed, when and by how much? • Are there correlates that may explain the pattern? 3. Is the population tracking a declining carrying capacity? • importance of density dependence • key question for recovery planning Inner Bay of Fundy Atlantic Salmon • Designated as endangered by COSEWIC and listed by GoC on Schedule 1 (SARA prohibitions in effect) • IBoF Salmon are different and distinct from other salmon populations • life history: • very high incidence of fish that mature after 1 winter at sea • high incidence of repeat spawning • genetic: • unique mitochrondrial DNA haplotype that has not been found in salmon outside the inner Bay of Fundy IBoF Atlantic Salmon: Area of Occupancy Big Salmon River E E Stewiacke River 0 25 50 kilometers Stewiacke River, NS: Salmon Data Year 1960 1970 1980 1990 2000 Rec. Catch (adults) Adult Counts (fence) Adult Counts (boat electrofishing) Adult M-R estimates Adult Age Comp. Electrofishing Big Salmon River, NB: Salmon Data Year 1960 1970 1980 1990 2000 Rec. Catch (adults) Adult Counts (fence) Adult Counts (snorkel) Adult Age Comp. Redd Counts Electrofishing Smolt Counts (Fence) Smolt Counts (M-R ests.) Smolt Age Comp. The Problem • We want to estimate the population size and trajectory from the available data • when did the decline occur? • is the population still declining? • when is extinction expected to occur? • From a Bayesian perspective can we avoid subjectivity (prior belief) when building the model? Two Model Components: 1. Annual abundance estimated by modeling catch-effort data and any auxiliary data that can be interpreted as an abundance index (Rago 2001) • Parameter estimates are obtained using ML • Parameter uncertainty is assessed using MCMC to derive posteriors 2. Forward projections (PVA) using Monte Carlo simulations using the estimated change in population size from one year to the next (Dennis et al. 1991) • Projections using the posteriors for abundance, and the mean and variance of log(lambda) • Advantages: uncertainty in parameter estimates is included in the PVA; parameter covariance is preserved The Model (catch equations) • We begin with the standard catch equation for a Type I fishery: −Ft ,s Ct,s = Nt,s (1− e ) • We assume Ft,s is proportional to the fishing effort in year t: F = q E t,s s t The Model (harvesting) • Calculated the proportion of the catch that was harvested • 0.824 for small salmon (1983 to 1990) • 0.758 for large salmon in 1983. • used as constants in analysis • could lead to overestimate of escapement in early years Esct,s = Nt,s − Ht,s The Model (fence counts) • Counts assumed complete in 1994 and 1995, but not in 1992 and 1993. • The 1992 and 1993 counts were adjusted upwards using the mark and recapture estimates. • The fence counts then equal to the number of fish returning to the river in each size category and each year: Fencet,s = Nt,s The Model (adult electrofishing) • electrofishing occurs after fishing and is an index of escapement • reported for size categories combined • modeled use the catch equation: qboat Eboat ,t Cboat,t = (1− e )∑ Esct,s s The Model (egg deposition) • mean fecundity of Stewiacke River salmon was calculated using data of Amiro (1990) • weighted by number at age and sex ratio • 2,364 eggs per small salmon • 7,545 eggs per large salmon • used as constants in this analysis Eggst = ∑ Esct,s fecs s The Model (juvenile electrofishing) • we use Beverton-Holt model to describe the relationship between juvenile abundance and egg deposition in the previous years: • age-0 density in year t is a index of egg deposition in year t-1 • age-1 density in year t is a index of egg deposition in year t-2 • age-2 density in year t is a index of egg deposition in year t-3 • two parameters estimated for each size class α Eggs P = a t−a−1 t,a α Eggs 1+ a t−a−1 R0a The Model: estimated parameters • We set up the model to estimate: • the log of the total escapement in each year (37 parameters) • the average proportion of the population that are small salmon (1 parameter) • the catchability coefficients for the recreational fisheries and boat electrofishing (3 parameters) • the slope at the origin and asymptotic level for the 3 ages of fish in the electrofishing data (6 parameters) • Total of 47 parameters Model Fitting: • Parameter estimates were obtained using maximum likelihood • Lognormal errors were assumed for all data except the adult mark-recapture experiments (hyper-geometric structure assumed) • σ could not be estimated for all data sets simultaneously • fixed σ at 0.33 for the electrofishing data and estimated σ for the other model components • Parameter estimates were obtained by minimizing the value of an objective function (O.B.V.) that is the sum of the negative log likelihoods (no weights): O.F.V. = −( fence + catch + electrofishing + boat + mr ) The Model (Bayesian component) • We assumed uniform bounded priors for all model parameters • Bounds were wide enough not to influence the fit. • We used 2,000,000 iterations after a burn in of 200,000 iterations. • We sampled every 2,000th iteration to derive the posterior distribution. • This level of thinning was sufficient to ensure that autocorrelation in the chain was not problematic. The Model (diagnostics) • We ran many iterations of the model using several starting values to ensure convergence to a global maximum • model is robust in this respect • Convergence of the Markov chain was inferred informally • by comparison of the posterior densities based on the first 1,000,000 iterations with those from the second 1,000,000 iterations • by comparison of the posterior densities from several chains Results (recreational fishing) Recreational Fishing Effort 10000 • effort increased through 8000 6000 4000 the '70's and early 80's Days Rod 2000 and then decreased 0 1970 1980 1990 2000 • catches are variable but Year increase in the 1980's Large Salmon Catch 600 400 • fitted catch tracks the 200 observed catch of Fish Number 0 reasonably well 1970 1980 1990 2000 • a near perfect fit is Year Salmon Salmon Catch obtained if the 2000 1500 proportion in each size 1000 500 category is estimated of Fish Number 0 for each year 1970 1980 1990 2000 Year Results (recreational fishing) • MLE's for the log of catchability coefficients are: - 9.522 (small) and –10.214 (large) • smaller fish are easier to catch Given an effort of 3000 rod days: the MLE and 80% B.C.I. for the catch 1.0 0.8 rates are: Small Salmon Large Salmon 0.8 0.6 Large salmon: 10.4% 0.6 0.4 (6.5 to 20.1%) 0.4 0.2 0.2 Probability Density Probability Small salmon: 19.7% Density Probability 0.0 0.0 (13.0 to 34.1%) -14 -12 -10 -9 -8 -14 -12 -10 -9 -8 log(q) log(q) Results (recreational harvest rates) • Shown MLE's and 95 % CI's for the annual harvest rates Recreational Fishery Exploitation Rate: Small Salmon 0.8 MLE's for harvest rates 0.6 increased to a maximum of 0.4 0.2 40.5 % (small salmon) and Rate Exploitation 0.0 21.8 % (large salmon) in 1970 1980 1990 2000 1983 and decreased Year thereafter Recreational Fishery Exploitation Rate: Large Salmon 0.8 Rates would be 0.6 underestimated if catch and 0.4 0.2 release increased during Rate Exploitation 0.0 time 1970 1980 1990 2000 Year Results (boat electrofishing) • Catches with the electrofishing boat ranged between 58 salmon (1991) and 0 (1997) • Effort ranged between 31.8 and 123 km • At an effort of 40 km, the expected catch is 1.4% Electrofishing 0.6 Boat of the population 0.4 Boat El ect r of ishi ng: l ar ge and small sal mon combi ned 60 0.2 40 Probability Density Probability 20 0.0 Number of Fish 0 -9 -8 -7 -6 1985 1990 1995 2000 log(q) Year Results (juvenile electrofishing) 200 • Between 27 and 44 150 age-0 sites electrofished 100 annually since 1984 50 0 • Consistent downward 1985 1990 1995 2000 trends are evident for 200 150 age-1 all three age classes 100 50 • no wild fry captured 0 1985 1990 1995 2000 since 1999 Density (number/100m^2) • slight increase in age-1 30 age-2 20 density in 2002 10 probably due to LGB 0 1985 1990 1995 2000 releases Year Results
Load more

Recommended publications
  • Barriers to Fish Passage in Nova Scotia the Evolution of Water Control Barriers in Nova Scotia’S Watershed
    Dalhousie University- Environmental Science Barriers to Fish Passage in Nova Scotia The Evolution of Water Control Barriers in Nova Scotia’s Watershed By: Gillian Fielding Supervisor: Shannon Sterling Submitted for ENVS 4901- Environmental Science Honours Abstract Loss of connectivity throughout river systems is one of the most serious effects dams impose on migrating fish species. I examine the extent and dates of aquatic habitat loss due to dam construction in two key salmon regions in Nova Scotia: Inner Bay of Fundy (IBoF) and the Southern Uplands (SU). This work is possible due to the recent progress in the water control structure inventory for the province of Nova Scotia (NSWCD) by Nova Scotia Environment. Findings indicate that 586 dams have been documented in the NSWCD inventory for the entire province. The most common main purpose of dams built throughout Nova Scotia is for hydropower production (21%) and only 14% of dams in the database contain associated fish passage technology. Findings indicate that the SU is impacted by 279 dams, resulting in an upstream habitat loss of 3,008 km of stream length, equivalent to 9.28% of the total stream length within the SU. The most extensive amount of loss occurred from 1920-1930. The IBoF was found to have 131 dams resulting in an upstream habitat loss of 1, 299 km of stream length, equivalent to 7.1% of total stream length. The most extensive amount of upstream habitat loss occurred from 1930-1940. I also examined if given what I have learned about the locations and dates of dam installations, are existent fish population data sufficient to assess the impacts of dams on the IBoF and SU Atlantic salmon populations in Nova Scotia? Results indicate that dams have caused a widespread upstream loss of freshwater habitat in Nova Scotia howeverfish population data do not exist to examine the direct impact of dam construction on the IBoF and SU Atlantic salmon populations in Nova Scotia.
    [Show full text]
  • Striped Bass Morone Saxatilis
    COSEWIC Assessment and Status Report on the Striped Bass Morone saxatilis in Canada Southern Gulf of St. Lawrence Population St. Lawrence Estuary Population Bay of Fundy Population SOUTHERN GULF OF ST. LAWRENCE POPULATION - THREATENED ST. LAWRENCE ESTUARY POPULATION - EXTIRPATED BAY OF FUNDY POPULATION - THREATENED 2004 COSEWIC COSEPAC COMMITTEE ON THE STATUS OF COMITÉ SUR LA SITUATION ENDANGERED WILDLIFE DES ESPÈCES EN PÉRIL IN CANADA AU CANADA COSEWIC status reports are working documents used in assigning the status of wildlife species suspected of being at risk. This report may be cited as follows: COSEWIC 2004. COSEWIC assessment and status report on the Striped Bass Morone saxatilis in Canada. Committee on the Status of Endangered Wildlife in Canada. Ottawa. vii + 43 pp. (www.sararegistry.gc.ca/status/status_e.cfm) Production note: COSEWIC would like to acknowledge Jean Robitaille for writing the status report on the Striped Bass Morone saxatilis prepared under contract with Environment Canada, overseen and edited by Claude Renaud the COSEWIC Freshwater Fish Species Specialist Subcommittee Co-chair. For additional copies contact: COSEWIC Secretariat c/o Canadian Wildlife Service Environment Canada Ottawa, ON K1A 0H3 Tel.: (819) 997-4991 / (819) 953-3215 Fax: (819) 994-3684 E-mail: COSEWIC/[email protected] http://www.cosewic.gc.ca Ếgalement disponible en français sous le titre Ếvaluation et Rapport de situation du COSEPAC sur la situation de bar rayé (Morone saxatilis) au Canada. Cover illustration: Striped Bass — Drawing from Scott and Crossman, 1973. Her Majesty the Queen in Right of Canada 2004 Catalogue No. CW69-14/421-2005E-PDF ISBN 0-662-39840-8 HTML: CW69-14/421-2005E-HTML 0-662-39841-6 Recycled paper COSEWIC Assessment Summary Assessment Summary – November 2004 Common name Striped Bass (Southern Gulf of St.
    [Show full text]
  • A Review of Ice and Tide Observations in the Bay of Fundy
    A tlantic Geology 195 A review of ice and tide observations in the Bay of Fundy ConDesplanque1 and David J. Mossman2 127 Harding Avenue, Amherst, Nova Scotia B4H 2A8, Canada departm ent of Physics, Engineering and Geoscience, Mount Allison University, 67 York Street, Sackville, New Brunswick E4L 1E6, Canada Date Received April 27, 1998 Date Accepted December 15,1998 Vigorous quasi-equilibrium conditions characterize interactions between land and sea in macrotidal regions. Ephemeral on the scale of geologic time, estuaries around the Bay of Fundy progressively infill with sediments as eustatic sea level rises, forcing fringing salt marshes to form and reform at successively higher levels. Although closely linked to a regime of tides with large amplitude and strong tidal currents, salt marshes near the Bay of Fundy rarely experience overflow. Built up to a level about 1.2 m lower than the highest astronomical tide, only very large tides are able to cover the marshes with a significant depth of water. Peak tides arrive in sets at periods of 7 months, 4.53 years and 18.03 years. Consequently, for months on end, no tidal flooding of the marshes occurs. Most salt marshes are raised to the level of the average tide of the 18-year cycle. The number of tides that can exceed a certain elevation in any given year depends on whether the three main tide-generating factors peak at the same time. Marigrams constructed for the Shubenacadie and Cornwallis river estuaries, Nova Scotia, illustrate how the estuarine tidal wave is reshaped over its course, to form bores, and varies in its sediment-carrying and erosional capacity as a result of changing water-surface gradients.
    [Show full text]
  • Isaac Deschamps Fonds (MG 1 Volume 258)
    Nova Scotia Archives Finding Aid - Isaac Deschamps fonds (MG 1 volume 258) Generated by Access to Memory (AtoM) 2.5.3 Printed: October 09, 2020 Language of description: English Nova Scotia Archives 6016 University Ave. Halifax Nova Scotia B3H 1W4 Telephone: (902) 424-6060 Fax: (902) 424-0628 Email: [email protected] http://archives.novascotia.ca/ https://memoryns.ca/index.php/isaac-deschamps-fonds Isaac Deschamps fonds Table of contents Summary information ...................................................................................................................................... 3 Administrative history / Biographical sketch .................................................................................................. 3 Scope and content ........................................................................................................................................... 3 Notes ................................................................................................................................................................ 4 Series descriptions ........................................................................................................................................... 4 - Page 2 - MG 1 volume 258 Isaac Deschamps fonds Summary information Repository: Nova Scotia Archives Title: Isaac Deschamps fonds ID: MG 1 volume 258 Date: 1750-1814, predominant 1756-1768 (date of creation) Physical description: 4 cm of textual records Dates of creation, Revised 2017-06-16 Carli LaPierre (items imported
    [Show full text]
  • Fundy Model Forest Composite of Water Quality Survey Results
    Fundy Model Forest ~Partners in Sustainability~ Report Title : Fundy Model Forest Composite of Water Quality Survey Results Author : McLaughlin, J. Year of project : 2000 Principal contact information: File Name: Soil_and_Water_2000_McLaughlin_ Fundy Model Forest Composite of Water Quality Survey Results Fundy Model Forest The Fundy Model Forest… …Partners in Sustainability “The Fundy Model Forest (FMF) is a partnership of 38 organizations that are promoting sustainable forest management practices in the Acadian Forest region.” Atlantic Society of Fish and Wildlife Biologists Canadian Institute of Forestry Canadian Forest Service City of Moncton Conservation Council of New Brunswick Fisheries and Oceans Canada Indian and Northern Affairs Canada Eel Ground First Nation Elgin Eco Association Elmhurst Outdoors Environment Canada Fawcett Lumber Company Fundy Environmental Action Group Fundy National Park Greater Fundy Ecosystem Research Group INFOR, Inc. J.D. Irving, Limited KC Irving Chair for Sustainable Development Maritime College of Forest Technology NB Department of the Environment and Local Government NB Department of Natural Resources NB Federation of Naturalists New Brunswick Federation of Woodlot Owners NB Premier's Round Table on the Environment & Economy New Brunswick School District 2 New Brunswick School District 6 Nova Forest Alliance Petitcodiac Sportsman's Club Red Bank First Nation Remsoft Inc. Southern New Brunswick Wood Cooperative Limited Sussex and District Chamber of Commerce Sussex Fish and Game Association Town of Sussex Université de Moncton University of NB, Fredericton - Faculty of Forestry University of NB - Saint John Campus Village of Petitcodiac Washademoak Environmentalists Fundy Model Forest Composite of Water Quality Survey Results. April 2000 By Julie McLaughlin B. Sc.(Eng) Acknowledgements I would like to thank the following people for their invaluable assistance in gathering the data required for this report.
    [Show full text]
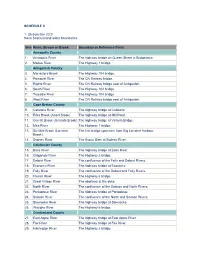
  • Nova Scotia Inland Water Boundaries Item River, Stream Or Brook
    SCHEDULE II 1. (Subsection 2(1)) Nova Scotia inland water boundaries Item River, Stream or Brook Boundary or Reference Point Annapolis County 1. Annapolis River The highway bridge on Queen Street in Bridgetown. 2. Moose River The Highway 1 bridge. Antigonish County 3. Monastery Brook The Highway 104 bridge. 4. Pomquet River The CN Railway bridge. 5. Rights River The CN Railway bridge east of Antigonish. 6. South River The Highway 104 bridge. 7. Tracadie River The Highway 104 bridge. 8. West River The CN Railway bridge east of Antigonish. Cape Breton County 9. Catalone River The highway bridge at Catalone. 10. Fifes Brook (Aconi Brook) The highway bridge at Mill Pond. 11. Gerratt Brook (Gerards Brook) The highway bridge at Victoria Bridge. 12. Mira River The Highway 1 bridge. 13. Six Mile Brook (Lorraine The first bridge upstream from Big Lorraine Harbour. Brook) 14. Sydney River The Sysco Dam at Sydney River. Colchester County 15. Bass River The highway bridge at Bass River. 16. Chiganois River The Highway 2 bridge. 17. Debert River The confluence of the Folly and Debert Rivers. 18. Economy River The highway bridge at Economy. 19. Folly River The confluence of the Debert and Folly Rivers. 20. French River The Highway 6 bridge. 21. Great Village River The aboiteau at the dyke. 22. North River The confluence of the Salmon and North Rivers. 23. Portapique River The highway bridge at Portapique. 24. Salmon River The confluence of the North and Salmon Rivers. 25. Stewiacke River The highway bridge at Stewiacke. 26. Waughs River The Highway 6 bridge.
    [Show full text]
  • Fishery Bulletin of the Fish and Wildlife Service V.53
    'I', . FISRES OF '!'RE GULF OF MAINE. 101 Description.-The hickory shad differs rather Bay, though it is found in practically all of them. noticeably from the sea herring in that the point This opens the interesting possibility that the of origin of its dorsal fin is considerably in front of "green" fish found in Chesapeake Bay, leave the the mid-length of its trunk; in its deep belly (a Bay, perhaps to spawn in salt water.65 hickory shad 13~ in. long is about 4 in. deep but a General range.-Atlantic coast of North America herring of that length is only 3 in. deep) ; in the fact from the Bay of Fundy to Florida. that its outline tapers toward both snout and tail Occurrence in the Gulf oj Maine.-The hickory in side view (fig. 15); and in that its lower jaw shad is a southern fish, with the Gulf of Maine as projects farther beyond the upper when its mouth the extreme northern limit to its range. It is is closed; also, by the saw-toothed edge of its belly. recorded in scientific literature only at North Also, it lacks the cluster of teeth on the roof of the· Truro; at Provincetown; at Brewster; in Boston mouth that is characteristic of the herring. One Harbor; off Portland; in Casco Ba3T; and from the is more likely to confuse a hickory shad with a shad mouth of the Bay of Fundy (Huntsman doubts or with the alewives, which it resembles in the this record), and it usually is so uncommon within position of its dorsal fin, in the great depth of its our limits that we have seen none in the Gulf body, in its saw-toothed belly and in the lack of ourselves.
    [Show full text]
  • South Western Nova Scotia
    Netukulimk of Aquatic Natural Life “The N.C.N.S. Netukulimkewe’l Commission is the Natural Life Management Authority for the Large Community of Mi’kmaq /Aboriginal Peoples who continue to reside on Traditional Mi’Kmaq Territory in Nova Scotia undisplaced to Indian Act Reserves” P.O. Box 1320, Truro, N.S., B2N 5N2 Tel: 902-895-7050 Toll Free: 1-877-565-1752 2 Netukulimk of Aquatic Natural Life N.C.N.S. Netukulimkewe’l Commission Table of Contents: Page(s) The 1986 Proclamation by our late Mi’kmaq Grand Chief 4 The 1994 Commendation to all A.T.R.A. Netukli’tite’wk (Harvesters) 5 A Message From the N.C.N.S. Netukulimkewe’l Commission 6 Our Collective Rights Proclamation 7 A.T.R.A. Netukli’tite’wk (Harvester) Duties and Responsibilities 8-12 SCHEDULE I Responsible Netukulimkewe’l (Harvesting) Methods and Equipment 16 Dangers of Illegal Harvesting- Enjoy Safe Shellfish 17-19 Anglers Guide to Fishes Of Nova Scotia 20-21 SCHEDULE II Specific Species Exceptions 22 Mntmu’k, Saqskale’s, E’s and Nkata’laq (Oysters, Scallops, Clams and Mussels) 22 Maqtewe’kji’ka’w (Small Mouth Black Bass) 23 Elapaqnte’mat Ji’ka’w (Striped Bass) 24 Atoqwa’su (Trout), all types 25 Landlocked Plamu (Landlocked Salmon) 26 WenjiWape’k Mime’j (Atlantic Whitefish) 26 Lake Whitefish 26 Jakej (Lobster) 27 Other Species 33 Atlantic Plamu (Salmon) 34 Atlantic Plamu (Salmon) Netukulimk (Harvest) Zones, Seasons and Recommended Netukulimk (Harvest) Amounts: 55 SCHEDULE III Winter Lake Netukulimkewe’l (Harvesting) 56-62 Fishing and Water Safety 63 Protecting Our Community’s Aboriginal and Treaty Rights-Community 66-70 Dispositions and Appeals Regional Netukulimkewe’l Advisory Councils (R.N.A.C.’s) 74-75 Description of the 2018 N.C.N.S.
    [Show full text]
  • Fundy Routes
    Fundy Region MAP ....................................................................................................Truro 1. La Plan che Rive r 2. Stew iack e Rive r 3. Rive r Heb 7 Route: No. 1 La Planche River Type: River Rating: easy Length: 30 kilometers round trip (18.5 miles) 2 days Portages: None Main bodies of water: La Planche River, Long Lake and Round Lake. Start: on the north side of the town of Amherst. Intermediate access: None Finish: Return by same route. This trip takes you up through a portion of the Tantramar Marshes. There is no white water and the current is not strong. There are no land marks that will be of any help and a number of side streams and ditches will make some navigational experience useful. The lower end of the river is tidal and the start should be made at high tide. The water levels are good except in extremely dry periods. On the north side of Long Lake you will pass the old abandoned ship railway that was built in the 1800’s to transport ships overland to the Northumberland Strait. The history of this can be found at Fort Beausejour on route 2 near Amherst. Fishing is good in certain areas and duck and muskrats are plentiful. There are not many good areas to camp along the river; but there are some good sites along the northeast shore of Long Lake. Detailed information: National Topographic Series Map No. 21H / 16E 8 Route: No. 2 Stewiacke River Type: River Rating: Moderate Length: 46 kilometers (28.7 miles) 2 days Portages: None Main bodies of water: Stewiacke River Start: Upper Stewiacke Intermediate access: at five locations.
    [Show full text]
  • Finally, Salmon Conservationists Can Enjoy Guilt-Free Fish
    p35to37_Meal Time F3__ 11/11/15 11:44 AM Page 35 LAND-BASED AQUACULTURE MEAL TIME! by Martin silverstone FINALLY, SALMON CONSERVATIONISTS CAN ENJOY GUILT-FREE FISH. DRIVING FROM THE SMALL VILLAGE OF BROOKLYN IN HANTS COUNTY, NOVA Scotia to the even smaller village of Centre Burlington, the countryside is so pretty it almost hurts. Farmhouses and wooden barns nestle among grassy fields, dotted with purple clover, orange hawkweed and yellow buttercups. Horses and cows nibble at lush grass. Cross over the Kennetcook River at low tide and its muddy red banks glisten in the morning sun. Later, on my way home, the tides pouring in from the Bay of Fundy will fill the waterway like a bathtub and it will sparkle, looking more like the thriving salmon river it once was. As I am here because of salmon, the bucolic beauty would normally not come as a surprise. Atlantic salmon rivers as a rule are beautiful wild places, but I’m not here to visit a river, my destination is a salmon farm. ) 3 ( e Not to say “traditional” or open net pen salmon farms, like those that dot the coast - u l b e l lines of Eastern Canada, Scotland and Norway, are ugly on the surface, but they are b a n i a t increasingly seen as a blight because of what happens beneath the sea. They have been s u s f o shown to pollute, cause disease and disrupt marine life, not only in their immediate y s e t r vicinity, but also up rivers where salmon farm escapees can dilute the genetic integrity of u o C wild fish (see Fundy Feedlots, ASJ , Spring 2011).
    [Show full text]
  • Freshwater Mussels of Nova Scotia
    NOVA SCOTIA MUSEUM Tur. F.o\Mli.Y of PKOVI.N C lAI~ MuSf::UMS CURATORIAL REPORT NUMBER 98 Freshwater Mussels of Nova Scotia By Derek 5. Dav is .. .. .... : ... .. Tourism, Culture and Heritage r r r Curatorial Report 98 r Freshwater Mussels of Nova Scotia r By: r Derek S. Davis r r r r r r r r r r Nova Scotia Museum Nova Scotia Department of Tourism, Culture and Heritage r Halifax Nova Scotia r April 2007 r l, I ,1 Curatorial Reports The Curatorial Reports of the Nova Scotia Museum make technical l information on museum collections, programs, procedures and research , accessible to interested readers. l This report contains the preliminary results of an on-going research program of the Museum. It may be cited in publications, but its manuscript status should be clearly noted. l. l l ,l J l l l Citation: Davis, D.S. 2007. Freshwater Mussels ofNova Scotia. l Curatorial Report Number 98, Nova Scotia Museum, Halifax: 76 p. l Cover illustration: Melissa Townsend , Other illustrations: Derek S. Davis i l l r r r Executive Summary r Archival institutions such as Museums of Natural History are repositories for important records of elements of natural history landscapes over a geographic range and over time. r The Mollusca collection of the Nova Scotia Museum is one example of where early (19th century) provincial collections have been documented and supplemented by further work over the following 143 years. Contemporary field investigations by the Nova Scotia r Museum and agencies such as the Nova Scotia Department of Natural Resources have allowed for a systematic documentation of the distribution of a selected group, the r freshwater mussels, in large portions of the province.
    [Show full text]
  • Social Studies Grade 3 Provincial Identity
    Social Studies Grade 3 Curriculum - Provincial ldentity Implementation September 2011 New~Nouveauk Brunsw1c Acknowledgements The Departments of Education acknowledge the work of the social studies consultants and other educators who served on the regional social studies committee. New Brunswick Newfoundland and Labrador Barbara Hillman Darryl Fillier John Hildebrand Nova Scotia Prince Edward Island Mary Fedorchuk Bethany Doiron Bruce Fisher Laura Ann Noye Rick McDonald Jennifer Burke The Departments of Education also acknowledge the contribution of all the educators who served on provincial writing teams and curriculum committees, and who reviewed and/or piloted the curriculum. Table of Contents Introduction ........................................................................................................................................................ 1 Program Designs and Outcomes ..................................................................................................................... 3 Overview ................................................................................................................................................... 3 Essential Graduation Learnings .................................................................................................................... 4 General Curriculum Outcomes ..................................................................................................................... 6 Processes ..................................................................................................................................................
    [Show full text]