DOCSLIB.ORG

TI-Nspire™ CAS / TI-Nspire™ CX CAS Reference Guide

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
TI-Nspire™ CAS / TI-Nspire™ CX CAS Reference Guide TI-Nspire™ CAS / TI-Nspire™ CX CAS Reference Guide This guidebook applies to TI-Nspire™ software version 3.9. To obtain the latest version of the documentation, go to education.ti.com/guides. Important Information Except as otherwise expressly stated in the License that accompanies a program, Texas Instruments makes no warranty, either express or implied, including but not limited to any implied warranties of merchantability and fitness for a particular purpose, regarding any programs or book materials and makes such materials available solely on an "as-is" basis. In no event shall Texas Instruments be liable to anyone for special, collateral, incidental, or consequential damages in connection with or arising out of the purchase or use of these materials, and the sole and exclusive liability of Texas Instruments, regardless of the form of action, shall not exceed the amount set forth in the license for the program. Moreover, Texas Instruments shall not be liable for any claim of any kind whatsoever against the use of these materials by any other party. License Please see the complete license installed in C:\Program Files\TI Education\<TI-Nspire™ Product Name>\license. © 2006 - 2014 Texas Instruments Incorporated 2 Contents Important Information 2 Expression Templates 5 Alphabetical Listing 12 A 12 B 21 C 24 D 47 E 57 F 65 G 73 I 78 L 86 M 100 N 107 O 115 P 117 Q 126 R 129 S 141 T 164 U 177 V 178 W 179 X 180 Z 181 Symbols 188 Empty (Void) Elements 212 Shortcuts for Entering Math Expressions 214 EOS™ (Equation Operating System) Hierarchy 216 Error Codes and Messages 218 3 Warning Codes and Messages 226 Support and Service 229 Texas Instruments Support and Service 229 Service and Warranty Information 229 Index 231 4 Expression Templates Expression templates give you an easy way to enter math expressions in standard mathematical notation. When you insert a template, it appears on the entry line with small blocks at positions where you can enter elements. A cursor shows which element you can enter. Position the cursor on each element, and type a value or expression for the element. Fraction template /p keys Example: Note: See also / (divide), page 190. Exponent template l key Example: Note: Type the first value, press l, and then type the exponent. To return the cursor to the baseline, press right arrow (¢). Note: See also ^ (power), page 190. Square root template /q keys Example: Note: See also √() (square root), page 200. Expression Templates 5 Nth root template /l keys Example: Note: See also root(), page 138. e exponent template u keys Example: Natural exponential e raised to a power Note: See also e^(), page 57. Log template /s key Example: Calculates log to a specified base. For a default of base 10, omit the base. Note: See also log(), page 96. Piecewise template (2-piece) Catalog > Example: Lets you create expressions and conditions for a two-piece piecewise function. To add a piece, click in the template and repeat the template. Note: See also piecewise(), page 119. 6 Expression Templates Piecewise template (N-piece) Catalog > Lets you create expressions and conditions for an N-piece Example: piecewise function. Prompts for N. See the example for Piecewise template (2-piece). Note: See also piecewise(), page 119. System of 2 equations template Catalog > Example: Creates a system of two equations. To add a row to an existing system, click in the template and repeat the template. Note: See also system(), page 163. System of N equations template Catalog > Lets you create a system of Nequations. Prompts for N. Example: See the example for System of equations template (2-equation). Note: See also system(), page 163. Absolute value template Catalog > Example: Note: See also abs(), page 12. Expression Templates 7 Absolute value template Catalog > dd°mm’ss.ss’’ template Catalog > Example: Lets you enter angles in dd°mm’ss.ss’’ format, where dd is the number of decimal degrees, mm is the number of minutes, and ss.ss is the number of seconds. Matrix template (2 x 2) Catalog > Example: Creates a 2 x 2 matrix. Matrix template (1 x 2) Catalog > Example: . Matrix template (2 x 1) Catalog > Example: Matrix template (m x n) Catalog > The template appears after you are prompted to Example: specify the number of rows and columns. 8 Expression Templates Matrix template (m x n) Catalog > Note: If you create a matrix with a large number of rows and columns, it may take a few moments to appear. Sum template (Σ) Catalog > Example: Note: See also Σ() (sumSeq), page 201. Product template (Π) Catalog > Example: Note: See also Π() (prodSeq), page 200. First derivative template Catalog > Example: The first derivative template can also be used to calculate first derivative at a point. Expression Templates 9 First derivative template Catalog > Note: See also d() (derivative), page 198. Second derivative template Catalog > Example: The second derivative template can also be used to calculate second derivative at a point. Note: See also d() (derivative), page 198. Nth derivative template Catalog > Example: The nth derivative template can be used to calculate the nth derivative. Note: See also d() (derivative), page 198. Definite integral template Catalog > Example: Note: See also∫() integral(), page 198. Indefinite integral template Catalog > Example: 10 Expression Templates Indefinite integral template Catalog > Note: See also ∫() integral(), page 198. Limit template Catalog > Example: Use − or (−) for left hand limit. Use + for right hand limit. Note: See also limit(), page 11. Expression Templates 11 Alphabetical Listing Items whose names are not alphabetic (such as +, !, and >) are listed at the end of this section, page 188. Unless otherwise specified, all examples in this section were performed in the default reset mode, and all variables are assumed to be undefined. A abs() Catalog > abs(Expr1) ⇒ expression abs(List1) ⇒ list abs(Matrix1) ⇒ matrix Returns the absolute value of the argument. Note: See also Absolute value template, page 7. If the argument is a complex number, returns the number’s modulus. Note: All undefined variables are treated as real variables. amortTbl() Catalog > amortTbl(NPmt,N,I,PV, [Pmt], [FV], [PpY], [CpY], [PmtAt], [roundValue]) ⇒ matrix Amortization function that returns a matrix as an amortization table for a set of TVM arguments. NPmt is the number of payments to be included in the table. The table starts with the first payment. N, I, PV, Pmt, FV, PpY, CpY, and PmtAt are described in the table of TVM arguments, page 175. • If you omit Pmt, it defaults to Pmt=tvmPmt (N,I,PV,FV,PpY,CpY,PmtAt). • If you omit FV, it defaults to FV=0. • The defaults for PpY, CpY, and PmtAt are the same as for the TVM functions. roundValue specifies the number of decimal places for rounding. Default=2. 12 Alphabetical Listing amortTbl() Catalog > The columns in the result matrix are in this order: Payment number, amount paid to interest, amount paid to principal, and balance. The balance displayed in row n is the balance after payment n. You can use the output matrix as input for the other amortization functions ΣInt() and ΣPrn(), page 201, and bal(), page 21. and Catalog > BooleanExpr1 and BooleanExpr2 ⇒ Boolean expression BooleanList1 and BooleanList2 ⇒ Boolean list BooleanMatrix1 and BooleanMatrix2 ⇒ Boolean matrix Returns true or false or a simplified form of the original entry. Integer1 andInteger2 ⇒ integer In Hex base mode: Compares two real integers bit-by-bit using an and operation. Internally, both integers are converted to signed, 64-bit binary numbers. When corresponding Important: Zero, not the letter O. bits are compared, the result is 1 if both bits are 1; otherwise, the result is 0. The returned value In Bin base mode: represents the bit results, and is displayed according to the Base mode. You can enter the integers in any number base. For a binary or hexadecimal entry, you must use the 0b or In Dec base mode: 0h prefix, respectively. Without a prefix, integers are treated as decimal (base 10). Note: A binary entry can have up to 64 digits (not counting the 0b prefix). A hexadecimal entry can have up to 16 digits. angle() Catalog > angle(Expr1) ⇒ expression In Degree angle mode: Returns the angle of the argument, interpreting the Alphabetical Listing 13 angle() Catalog > argument as a complex number. Note: All undefined variables are treated as real variables. In Gradian angle mode: In Radian angle mode: angle(List1) ⇒ list angle(Matrix1) ⇒ matrix Returns a list or matrix of angles of the elements in List1 or Matrix1, interpreting each element as a complex number that represents a two-dimensional rectangular coordinate point. ANOVA Catalog > ANOVA List1,List2[,List3,...,List20][,Flag] Performs a one-way analysis of variance for comparing the means of two to 20 populations. A summary of results is stored in the stat.results variable. (page 159) Flag=0 for Data, Flag=1 for Stats Output variable Description stat.F Value of the F statistic stat.PVal Smallest level of significance at which the null hypothesis can be rejected stat.df Degrees of freedom of the groups stat.SS Sum of squares of the groups stat.MS Mean squares for the groups stat.dfError Degrees of freedom of the errors 14 Alphabetical Listing Output variable Description stat.SSError Sum of squares of the errors stat.MSError Mean square for the errors stat.sp Pooled standard deviation stat.xbarlist Mean of the input of the lists stat.CLowerList 95% confidence intervals for the mean of each input list stat.CUpperList 95% confidence intervals for the mean of each input list ANOVA2way Catalog > ANOVA2way List1,List2[,List3,…,List10][,levRow] Computes a two-way analysis of variance for comparing the means of two to 10 populations.
Load more

Recommended publications
  • Investigation 6.6.2 - Gradian Measure
    Investigation 6.6.2 - Gradian measure Have you ever wondered why we have 360 degrees in a circle when our number system is base 10? Why not divide the circle into 10 angular units? Or 100? The notion of the “degree” as the base angular unit of measure is generally attributed to the Babylonians. The Babylonian numerical system was sexagesimal (base 60). The number “360” played an essential role in their calendar as it is close to the number of days in a year. Another hypothesis is that the circle divides more naturally into six parts than it does four or ten. Try drawing diameters through a circle cutting it into even parts. I. 6 equal parts II. 4 equal parts III. 10 equal parts Then draw chords by connecting consecutive diameter endpoints. Which method produces equilateral triangles? Which dissected circle has chords congruent to its radius? Now find the central angle of each dissection. Which is most closely related to the Babylonian sexagesimal number system? Now suppose we wanted to derive an angular unit of measure more closely related to our base 10 decimal system. Let us begin by dividing a right angle into 100 units, called “gradians”. (You may have this system on your calculator, denoted “grad”.) a. How many gradians are in one whole circle? b. Convert 180° into gradians. c. How many degrees make 50 gradians? If societies in science fiction have differing number of days in their respective years due to different planetary orbits, it would stand to reason that their methods for measuring angles and circles might be different from our system.
    [Show full text]
  • Aircomforttm
    AirComfort TM Weather and Climate Lesson Plan AirComfort TM Weather and Climate Lesson Plan from HamiltonBuhl® Table of Contents Introduction . 3 Setup . .4 Data Format . 4 Activity 1: Differentiating Weather and Climate . 5 Blank Venn Diagram (Illustration A) 6 Venn Diagram with Answers (Illustration B) 7 For Further Discussion 8 Activity 2: Temperature Scales Conversion . .9 Quick Method and Exact Method Formulae 10 Blank Typical Temperatures Chart 10 Typical Temperatures Chart with Answers 11 For Further Discussion 12 Activity 3: Hangman Joke . .13 Blank Hangman Joke (Illustration C) 14 Hangman Joke with Answer (Illustration D) 15 For Further Discussion 16 Activity 4: Crossword Puzzle . 17. Blank Crossword Puzzle (Illustration E) 18 Crossword Puzzle with Answers (Illustration F) 19 For Further Discussion 20 Activity 5: Weather Measurement Tools . 21. Blank Weather Tools (Worksheet 1) 22 Weather Tools Answers (Worksheet 2) 23 Activity 6: Tracking and Comparing Weather Data . .24 Blank Plotting Chart (Worksheet 3) 25 Examples Plotting Chart (Worksheet 4) 26 For Further Discussion 27 The Fun Doesn’t Stop . 28 Certificate of Achievement . 29 . Sources . .30 TMTM Weather and Climate Lesson Plan AirComfortAirComfort from HamiltonBuhl® Weather and Climate Lesson Plan from HamiltonBuhl® Introduction Table of Contents This HamiltonBuhl® Weather Climate Lesson Plan is made for use with Introduction . 3 AirComfortTM. The educator uses this document as a guide to instruct Setup . .4 elementary school children to enrich their science and math education. Data Format . 4 Activities use these disciplines: Activity 1: Differentiating Weather and Climate . 5 Blank Venn Diagram (Illustration A) 6 1. Internet Usage Venn Diagram with Answers (Illustration B) 7 For Further Discussion 8 2.
    [Show full text]
  • Engilab Units 2018 V2.2
    EngiLab Units 2021 v3.1 (v3.1.7864) User Manual www.engilab.com This page intentionally left blank. EngiLab Units 2021 v3.1 User Manual (c) 2021 EngiLab PC All rights reserved. No parts of this work may be reproduced in any form or by any means - graphic, electronic, or mechanical, including photocopying, recording, taping, or information storage and retrieval systems - without the written permission of the publisher. Products that are referred to in this document may be either trademarks and/or registered trademarks of the respective owners. The publisher and the author make no claim to these trademarks. While every precaution has been taken in the preparation of this document, the publisher and the author assume no responsibility for errors or omissions, or for damages resulting from the use of information contained in this document or from the use of programs and source code that may accompany it. In no event shall the publisher and the author be liable for any loss of profit or any other commercial damage caused or alleged to have been caused directly or indirectly by this document. "There are two possible outcomes: if the result confirms the Publisher hypothesis, then you've made a measurement. If the result is EngiLab PC contrary to the hypothesis, then you've made a discovery." Document type Enrico Fermi User Manual Program name EngiLab Units Program version v3.1.7864 Document version v1.0 Document release date July 13, 2021 This page intentionally left blank. Table of Contents V Table of Contents Chapter 1 Introduction to EngiLab Units 1 1 Overview ..................................................................................................................................
    [Show full text]
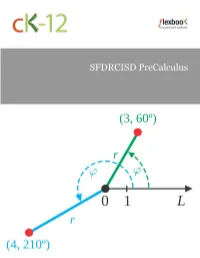
  • SFDRCISD Precalculus
    SFDRCISD PreCalculus SFDR Precalculus EPISD Precalculus Team Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) www.ck12.org AUTHORS SFDR Precalculus To access a customizable version of this book, as well as other EPISD Precalculus Team interactive content, visit www.ck12.org CK-12 Foundation is a non-profit organization with a mission to reduce the cost of textbook materials for the K-12 market both in the U.S. and worldwide. Using an open-source, collaborative, and web-based compilation model, CK-12 pioneers and promotes the creation and distribution of high-quality, adaptive online textbooks that can be mixed, modified and printed (i.e., the FlexBook® textbooks). Copyright © 2015 CK-12 Foundation, www.ck12.org The names “CK-12” and “CK12” and associated logos and the terms “FlexBook®” and “FlexBook Platform®” (collectively “CK-12 Marks”) are trademarks and service marks of CK-12 Foundation and are protected by federal, state, and international laws. Any form of reproduction of this book in any format or medium, in whole or in sections must include the referral attribution link http://www.ck12.org/saythanks (placed in a visible location) in addition to the following terms. Except as otherwise noted, all CK-12 Content (including CK-12 Curriculum Material) is made available to Users in accordance with the Creative Commons Attribution-Non-Commercial 3.0 Unported (CC BY-NC 3.0) License (http://creativecommons.org/ licenses/by-nc/3.0/), as amended and updated by Creative Com- mons from time to time (the “CC License”), which is incorporated herein by this reference.
    [Show full text]
  • Unit 3 – Trigonometric Functions Unit 3 – Trigonometric Functions
    UNIT 3 – TRIGONOMETRIC FUNCTIONS UNIT 3 – TRIGONOMETRIC FUNCTIONS .................................................................................................................................. 1 ESSENTIAL CONCEPTS OF TRIGONOMETRY ......................................................................................................................... 4 INTRODUCTION................................................................................................................................................................................. 4 WHAT IS TRIGONOMETRY? ............................................................................................................................................................... 4 WHY TRIANGLES? ............................................................................................................................................................................ 4 EXAMPLES OF PROBLEMS THAT CAN BE SOLVED USING TRIGONOMETRY ........................................................................................... 4 GENERAL APPLICATIONS OF TRIGONOMETRIC FUNCTIONS ................................................................................................................ 4 WHY TRIGONOMETRY WORKS.......................................................................................................................................................... 4 EXTREMELY IMPORTANT NOTE ON THE NOTATION OF TRIGONOMETRY ............................................................................................
    [Show full text]
  • A Modeling Approach to Calculus
    626 APPENDIX B. TRIGONOMETRY BASICS B.2 Measuring Arbitrary Angles B.2.1 Angles and Rotation In the previous section, we focused on the trigonometry of right triangles, which involve angles smaller than a right angle. The more significant use of measuring angles involve angles of rotation which can be significantly greater than 90 degrees. Before we proceed, we need to discuss how angles are measured. Have you ever considered why we measure angles in degrees? What is so special about a degree? One thing nice about the number 360 is that it has so many factors, including 2, 3, 4, 5, 6, 8, 9, 10 and 12. (That only misses 7 and 11!) This makes it easy to divide into fractions that simplify cleanly with integers. Having an easily divisible number that is so close to the number of days in the year, so that 1 degree is close to the change in the daily position of stars in the sky, would have been convenient to ancient astronomers. What other ways are there to measure rotations? If a right angle is considered the fundamental unit, then we might consider measuring an angle as a percentage of a right angle, so that 90 degrees counts as 100 percent. This idea led to the development of what is called a gradian. So an angle of 1 gradian is exactly 1 percent of a right angle, and there are 400 gradians in a circle. Alternatively, if we think of a full rotation as the fundamental unit, then we might measure an angle as a fraction of a rotation.
    [Show full text]
  • TI-36X Pro Calculator Important Information
    TI-36X Pro Calculator Important information............................................................. 2 Examples............................................................................... 3 Switching the calculator on and off........................................ 3 Display contrast ..................................................................... 3 Home screen ......................................................................... 3 2nd functions ......................................................................... 5 Modes.................................................................................... 5 Multi-tap keys......................................................................... 8 Menus.................................................................................... 8 Scrolling expressions and history .......................................... 9 Answer toggle...................................................................... 10 Last answer ......................................................................... 10 Order of operations.............................................................. 11 Clearing and correcting........................................................ 13 Fractions.............................................................................. 13 Percentages......................................................................... 15 EE key ................................................................................. 16 Powers, roots and inverses ................................................
    [Show full text]
  • Trigonometry Introducing Mathematics (Fx350ex/Fx82ex)
    Barry Kissane Module 4 Trigonometry A calculator is a useful tool for many aspects of trigonometry, both for solving problems involving measurement and understanding relationships among angles. To start with check that your calculator is set to use degrees (by looking for a small D symbol on the display). Use T to change it if necessary. Start this module in Calculate mode, by tapping p1. Trigonometry and right triangles Definitions of trigonometric functions can be based on right triangles, such as the one shown below, for which C is a right angle. A C B AC BC AC For this triangle, sine B = , cosine B = and tangent B = . AB AB BC In addition, because the triangle is right angled, the Theorem of Pythagoras allows us to see the relationship between the lengths of the two sides (AC and BC) and the hypotenuse (AB): AC 2 BC 2 AB2 Together, these relationships allow us to determine all the sides and the angles of a right triangle, even when only some of the information is known. For example, if we know that angle B is 38o and that AB = 4.2 m, we can find the length of AC using the definition of sine above: AC AC sin B = = , so AC = 4.2 sin B. AB 4.2 Computations like this are easily performed on the calculator. It is a good practice to include the bracket after the angle size, even though the calculator will calculate correctly without it. Notice that it is not necessary to use a multiplication sign in this case to find that AC ≈ 2.59 m.
    [Show full text]
  • Engineering Calculations Lecture Notes – Part 1
    YILDIZ TECHNICAL UNIVERSITY, FACULTY OF CIVIL ENG. DEPT. OF GEOMATIC ENG. ENGINEERING CALCULATIONS LECTURE NOTES – PART 1 Assoc. Prof. Dr. Bahattin Erdoğan and Assoc.Prof.Dr.Nursu Tunalıoğlu Spring Term Engineering Calculations | 1 Contents 1 INTRODUCTION TO GEOMATICS ................................................................................................................ 2 Types of survey .......................................................................................................................................... 2 Standards and Specifications..................................................................................................................... 5 2 MEASURING SYSTEM and UNITS ................................................................................................................ 7 Basic SI Units.............................................................................................................................................. 8 The Units for Length, Area and Volume ................................................................................................ 8 SI Units for Plane Angles ........................................................................................................................ 9 Measured Angles: ................................................................................................................................ 10 Degree ................................................................................................................................................
    [Show full text]
  • How to Measure Navigational Velocity Using the Metric System by Stanley M
    Gradians, Not Degrees: How to Measure Navigational Velocity Using the Metric System by Stanley M. Max Lecturer, Department of Mathematics, Towson University Certified Metrication Specialist, U.S. Metric Association Abstract Even in countries where the metric system has been long established, knots are used to measure navigational velocity on the sea and in the air. This is surprising because a knot, which equals one nautical mile per hour, is not a metric unit. However, the knot is based upon the size and shape of the Earth, so this unit has natural appeal to navigators. Does a method exist to use the metric unit of kilometers per hour for measuring navigational velocity that is also based upon the size and shape of the Earth, and which would therefore provide equal appeal to navigators? Yes it does, provided that angular measurement is performed using gradians (also called gons) instead of degrees. Measuring navigational velocity In air and sea navigation throughout much of the world, horizontal velocity is measured in knots (kn). This is not a metric unit, which is to say that it does not comply with the international standards officially known as the International System of Units (known in short as SI). For a knot, the metric equivalent is kilometers per hour (km/h). I strongly advocate for the metric system, and I decry the continued and stubborn refusal of the United States to fully metricate its system of weights and measures. I believe that having to learn two systems of measurement — one of which (the inch-pound system) is archaic and inefficient — very much contributes to the poor mathematical skills exhibited by Americans.
    [Show full text]
  • Learning Mathematics with Graphics Calculators 1 Barry Kissane & Marian Kemp
    PREFACE Over 40 years, calculators have evolved from being computational devices for scientists and engineers to becoming important educational tools. What began as a tool to answer numerical questions has evolved to become an affordable, powerful and flexible environment for students and their teachers to explore mathematical ideas and relationships. CASIO’s invention of a graphics screen on scientific calculators almost 30 years added significant educational power to these devices. Following many years of advice from experienced teachers, the CASIO fx-9860GII series of calculators include substantial mathematical capabilities, innovative use of a graphics screen for mathematical purposes and extensive use of natural displays of mathematical notation. Continuing this evolutionary process, the CASIO fx-CG 20 includes a colour graphics screen and innovative applications to enhance its educational value. This publication comprises a series of modules to help make best use of the opportunities for mathematics education afforded by these developments. The focus of the modules is on the use of the calculators in the development of students’ understanding of mathematical concepts and relationships, as an integral part of the development of mathematical meaning for the students. The calculator is not just a device for computation, once the mathematics has been understood. It is now best thought of as a laboratory in which students can experiment with mathematical ideas and deepen their understanding of the mathematics involved. The similarities between the two calculator models allows users of either calculator to make use of the modules, except for three special modules which require the enhanced features of the CASIO fx-CG 20, the colour graphics calculator.
    [Show full text]
  • Angle Measurement by Myron Berg Dickinson State University Abstract
    Angle Measurement By Myron Berg Dickinson State University abstract • This PowerPoint deck was created for a presentation. • I discuss some ways other than degrees or radians in which angles are measured • Instead of using a radius of 1 to create radians, I discusses the results of using 1 as the circumference or area of a circle to create an alternative unit of measure. Then I examined whether these units have any advantage, including greater simplicity, when compared to the values that result from radians. Goals • Provide background information for instruction about angle measurement • Cover some strategies for helping students understand radian measure Overview • History of angle measurements • Common methods used to measure angles today • Cyclical angles • Advantages of using radians to measure angles • Helping students remember angle measurement values The Unit Circle • Expecting it to be simple – but can be a struggle Angle measurement strategies Slope Examples of grade: Grade % not evenly spaced Degrees vs Grade 50 45 40 35 30 25 20 degrees 15 10 5 0 0 20 40 60 80 100 120 grade Angles formed by repeated bisection • 256 units would be closest to 360 Compass Points use 16 divisions Wind Directions Using a scale with 0 and 360 being north Degrees Circular Reasoning to describe Circles • Why is there 360 degrees in a circle? • Because 4 right angles make a circle, and each right angle is 90° • Why is there 90 degrees in a right angle? • Because there are 360 degrees in a circle and a right angle is ¼ of a circle 360° • Reason for using 360 is unknown • 365 days in a year could be explanation • Babylonians divided circle using the angle of an equilateral triangle, then subdivided that using their sexagesimal numeric system • They inherited sexagesimal from Sumerians, who developed it around 2000 B.C.
    [Show full text]