Entropy and Energy Dissipation of a Braided River System
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Revised Master Plan and Zoning Regulations for Greater Tezpur -2031
REVISED MASTER PLAN AND ZONING REGULATIONS FOR GREATER TEZPUR -2031 PREPARED BY DISTRICT OFFICE TOWN AND COUNTRY PLANNING GOVERNMENT OF ASSAM TEZPUR: ASSAM SCHEDULE a) Situation of the Area : District : Sonitpur Sub Division : Tezpur Area : 12,659Hect. Or 126.60 Sq Km. TOWN & VILLAGES INCLUDED IN THE REVISED MASTER PLAN AREA FOR GREATER TEZPUR – 2031 MOUZA TOWN & VILLAGES Mahabhairab Tezpur Town & 1. Kalibarichuk, 2. Balichapari, 3. Barikachuburi, 4. Hazarapar Dekargaon, 5. Batamari, 6. Bhojkhowa Chapari, 7. Bhojkhowa Gaon, 8. Rajbharal, 9. Bhomoraguri Pahar, 10. Jorgarh, 11. Karaiyani Bengali, 12. Morisuti, 13. Chatai Chapari, 14. Kacharipam, 15. Bhomoraguri Gaon, 16. Purani Alimur, 17. Uriamguri, 18. Alichinga Uriamguri. Bhairabpad 19. Mazgaon, 20. Dekargaon, 21. Da-parbatia, 22. Parbatia, 23. Deurigaon, 24. Da-ati gaon, 25. Da-gaon pukhuria, 26. Bamun Chuburi, 27. Vitarsuti, 28. Khanamukh, 29. Dolabari No.1, 30. Dolabari No.2, 31. Gotlong, 32. Jahajghat 33. Kataki chuburi, 34. Sopora Chuburi, 35. Bebejia, 36. Kumar Gaon. Halleswar 37. Saikiachuburi Dekargaon, 38. Harigaon, 39. Puthikhati, 40. Dekachuburi Kundarbari, 41. Parowa gaon, 42. Parowa TE, 43. Saikia Chuburi Teleria, 44. Dipota Hatkhola, 45. Udmari Barjhar, 46. Nij Halleswar, 47. Halleswar Devalaya, 48. Betonijhar, 49. Goroimari Borpukhuri, 50. Na-pam, 51. Amolapam, 52. Borguri, 53. Gatonga Kahdol, 54. Dihingia Gaon, 55. Bhitar Parowa, 56. Paramaighuli, 57. Solmara, 58. Rupkuria, 59. Baghchung, 60. Kasakani, 61. Ahatguri, 62. Puniani Gaon, 63. Salanigaon, 64. Jagalani. Goroimari 65. Goroimari Gaon, 66. Goroimari RF 1 CHAPTER – I INTRODUCTION Tezpur town is the administrative H/Q of Sonitpur Dist. Over the years this town has emerged as on the few major important urban centers of Assam & the North Eastern Region of India. -

Conservation of Gangetic Dolphin in Brahmaputra River System, India
CONSERVATION OF GANGETIC DOLPHIN IN BRAHMAPUTRA RIVER SYSTEM, INDIA Final Technical Report A. Wakid Project Leader, Gangetic Dolphin Conservation Project Assam, India Email: [email protected] 2 ACKNOWLEDGEMENT There was no comprehensive data on the conservation status of Gangetic dolphin in Brahmaputra river system for last 12 years. Therefore, it was very important to undertake a detail study on the species from the conservation point of view in the entire river system within Assam, based on which site and factor specific conservation actions would be worthwhile. However, getting the sponsorship to conduct this task in a huge geographical area of about 56,000 sq. km. itself was a great problem. The support from the BP Conservation Programme (BPCP) and the Rufford Small Grant for Nature Conservation (RSG) made it possible for me. I am hereby expressing my sincere thanks to both of these Funding Agencies for their great support to save this endangered species. Besides their enormous workload, Marianne Dunn, Dalgen Robyn, Kate Stoke and Jaimye Bartake of BPCP spent a lot of time for my Project and for me through advise, network and capacity building, which helped me in successful completion of this project. I am very much grateful to all of them. Josh Cole, the Programme Manager of RSG encouraged me through his visit to my field area in April, 2005. I am thankful to him for this encouragement. Simon Mickleburgh and Dr. Martin Fisher (Flora & Fauna International), Rosey Travellan (Tropical Biology Association), Gill Braulik (IUCN), Brian Smith (IUCN), Rundall Reeves (IUCN), Dr. A. R. Rahmani (BNHS), Prof. -
Bangladesh-India Protocol Routes
TEJPUR NAGALAND SILGHAT 31C BANGLADESH-INDIA I N D I A A S S A M 36 JOGIGHOPA DISPUR 37 31 PANDU DHUBRI 37 PROTOCOL ROUTES KOHIMA 40 SHISHUMARA SHILLONG 31 51 CHILMARI M E G H A L A Y A 53 MANIPUR ZAKIGANJ LAKHIPUR 34 BAHADURABAD 53 IMPHAL KARIMGANJ MARKULI FENCHUGANJ SHERPUR FARAKKA B A N G L A D E S H AJMIRIGANJ DHULIAN GODAGARI SIRAJGANJ RAJSHAHI 54 N BHAIRAB 44 BAZAR ASHUGANJ BAGHABARI TRIPURA ARICHA AGARTALA AIZWAL DHAKA MIZORAM NARAYANGANJ Legend Declared National waterway Proposed National waterway 2 CHANDPUR Protocol route Road Rail NH 51 35 KHULNA BARISAL Protocol route distances CHALNA KAUKHALI KOLKATA Kolkata - Guwahati/Pandu..….. 1535 km MONGLA 6 Kolkata - Karimganj............…....1318 km 41 HALDIA Dhulian-Rajshahi...............….........78 km NAMKHANA Bay of Bengal Myanmar(Burma) Summary of the Protocol Protocol on Inland Water Transit and Trade between Bangladesh and India In accordance with Article viii of the trade Agreement between Bangladesh & India Protocol on Inland Water Transit and Trade (PIWT&T) between the countries was signed to make mutually beneficial arrangements for the use of their waterways for commerce between the two countries and for passage of goods between two places in one country and to third countries through the territory of the other under the terms mutually agreed upon. In such cases, fees and charges, if leviable as per international agreements, conventions or practices, may be applied and transit guarantee regime may be established through mutual consultations. The Protocol was first signed in 1972 and since then it has been continuing without any interruption. -

Expanding Tradable Benefits of Inland Waterways Case of India
Expanding Tradable Benefits of Inland Waterways Case of India Published By D-217, Bhaskar Marg, Bani Park, Jaipur 302016, India Tel: +91.141.2282821, Fax: +91.141.2282485 Email: [email protected], Web site: www.cuts-international.org With the support of © CUTS International, 2017 First published: December 2017 This document has been produced by CUTS International Printed in India by M S Printer, Jaipur This document is the output of the study designed and implemented by CUTS International and its strategic partners – Royal Society for Protection of Nature (RSPN), South Asia Watch on Trade, Economics and Environment (SAWTEE) and Unnayan Shamannay which contributes to the project ‘Expanding tradable benefits of trans-boundary water: Promoting navigational usage of inland waterways in Ganga and Brahmaputra basins’. More details are available at: www.cuts- citee.org/IW/ This publication is made possible with the support of The Asia Foundation. The views and opinions expressed in this publication is that of CUTS International and partners and not of The Asia Foundation. #1715 2 Contents Acknowledgement...................................................................................................... 5 Abbreviations ............................................................................................................ 6 Contributors .............................................................................................................. 7 Executive Summary................................................................................................... -

A Study on Indian Participation in the Protocol of Inland Water Transit & Trade (PIWTT)
A study on Indian participation in the Protocol of Inland Water Transit & Trade (PIWTT) Sponsored by the High Commission of India in Bangladesh and Investment & Technology Promotion Division, Ministry of External Affairs, Government of India Mahboob Ahmed Senior Consultant and Managing Director Shipwrights Resources Limited House # 102 (1st Floor) Road # 102, Block-F Banani Dhaka-1213, Bangladesh 1 Table of Contents Contents Page No. I Introduction to the Study 3 Section-I Ii Points of Entry & Exit on the PIWTT route 5 iii River Routes & Ports of Call 6 Section-II iv 7 Regulatory & Procedural requirement for Indian Vessels V IWAI rules & Applicable vessel & cargo related charges 8 9 BIWTA rules & Applicable vessel & cargo related charges vi Applicable Charges for Indian vessels for transit & 11 transshipment (by modal): vii Customs & Immigration procedures in the PIWTT route 12 viii Freights earned by the Indian vessels 13 Section-III ix Review of transit/ transshipment activity by Indian Shippers 14 under PIWTT x Current outlook of transit & transshipment activity 17 Section-IV xi Evaluation of dismal participation of Indian Vessels under PIWTT Section-V 21 State of Transshipment Infrastructures 24 Section-VI xii Challenges & Opportunities 26 2 A Study on Indian Participation in Transit and Transshipment trade under the PIWTT (The following report had been developed after extensive interactions with number of Indian shippers and ship operators based in Kolkata, IWAI, State & Central Government officials, political personalities and private business people accumulated in a recent FICI NE connectivity Summit held in Agartala (21-23 Sept., 2016), Tripura Introduction The PIWTT has taken a new dimension in recent times for east west connectivity by inland waterways. -
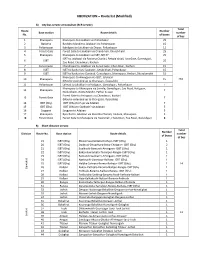
UBERIZATION – Route List (Modified)
UBERIZATION – Route list (Modified) A) City bus service at Guwahati (SCR service) Total Route Number Base station Route details number No. of buses of bus 1 Khanapara Khanapara to Jalukbari via Paltanbazar 25 2 Basistha Basistha Mandir to Jalukbari via Paltanbazar 15 3 Paltanbazar Kahilipara to Jalukbari via Dispur, Paltanbazar 12 4 Forest Gate Forest Gate to Jalukbari via Chandmari, Church field 25 5 Khanapara Khanapara to Jalukbari via ISBT, NH 37 25 ISBT to Jalukbari via Basistha Chariali, Beltola tiniali, Last Gate, Ganeshguri, 6 ISBT 20 Zoo Road, Chandmari, Kachari 7 Forest Gate Chandrapur to Jalukbari via Forest Gate, Chandmari, Kachari 15 8 ISBT ISBT to Kachari via Saukuchi, Serab bhati, Paltanbazar 15 9 ISBT ISBT to Kachari via Garchuk, Ganeshpara, Dhirenpara, Ambari, Bharalumukh 15 Khanapara to Amingaon via ISBT, Jalukbari 10 Khanapara 15 233 (May be extended up to Changsari, if possible) 11 Paltanbazar Lalmati to Jalukbari via Hatigaon, Ganeshguri, Paltanbazar 7 Khanapara to Khanapara via Sixmile, Ganeshguri, Zoo Road, Hatigaon, 12 Khanapara 7 Narikolbasti, Geeta Mandir, Pathar Kuwari Forest Gate to Amingaon via Chandmari, Kachari 13 Forest Gate 7 (May be extended up to Changsari, if possible) 14 ISBT (Ghy) ISBT (Ghy) to Hajo via Adabari 7 15 ISBT (Ghy) ISBT (Ghy) to Soalkuchi via Adabari 5 16 Soygaon Soygaon to Adabari 5 17 Khanapara Byrnihat to Jalukbari via Basistha Chariali, Lakhara, Khanapara 5 18 Forest Gate Forest Gate to Khanapara via Noonmati, Chandmari, Zoo Road, Ganeshguri 8 B) Short distance service Total Number -

Tender of Bank Protection at Silghat
FOR BANK PROTECTION WORK AT SILGHAT TERMINAL ON NATIONAL WATERWAY - 2 TENDER No . IWAI/GHY/3(13)/SIL/2013-14 INLAND WATERWAYS AUTHORITY OF INDIA (Ministry of Shipping, Govt. of India ) Pandu Port Complex, Pandu Port, Guwahati – 781012 (ASSAM). Telephone Nos. 0361-2570055, 2570099 Page 1 of 55 INLAND WATERWAYS AUTHORITY OF INDIA (Ministry of Shipping, Govt. of India ) Pandu Port Complex Pandu Port, Guwahati – 781 012, (ASSAM). Telephone Nos. 0361-2570055, 2570099 No: Date: To Sub: Tender document for bank protection work at Silghat terminal of IWAI on National Waterway - 2 Ref: Your letter no. Dated Sir, With reference to your letter cited on the above-mentioned subject, please find enclosed herewith one set of tender document for the subject work. You are requested to go through the terms and conditions carefully and also visit the site to familiarize and submit your tender as per procedure explained therein. The last date for receipt of tender is 19.8.2013 up to 3.00 PM at IWAI, Guwahati Issuance of tender document will not construe that such bidders are automatically considered qualified. Yours faithfully Director Page 2 of 55 INLAND WATERWAYS AUTHORITY OF INDIA (Ministry of Shipping, Govt. of India ) Pandu Port Complex Pandu Port, Guwahati – 781012, (ASSAM). Telephone Nos. 0361-2570055, 2570099 , NOTICE INVITING TENDER No. IWAI/GHY/3(13)/SIL/2013-14 Name of Work: Tender document for bank protection work at Silghat terminal of IWAI on National Waterway - 2 1. Estimated Cost of the work and EMD requirement are as under: Sl.No Name of Works Estimated Cost EMD (Rs.) (Rs) Tender document for bank pro tection 193750.00 4000/- A. -

Bharatmala Pariyojana October 2017 Bharatmala Pariyojana
Bharatmala Pariyojana October 2017 Bharatmala Pariyojana Why Bharatmala Components of Bharatmala Bharatmala Network identification methodology Highlights of Bharatmala Pariyojana Impact of Bharatmala 2 Visionary Corridor-based development initiated under National Highways Development Prog. NHDP-I: Golden Quadrilateral NHDP-II: NS-EW Corridors Later Phases of NHDP were taken up as projects instead of corridors 3 Illustration of infrastructure inconsistencies: Mumbai – Kolkata corridor Kolkata –Mumbai NH 6 Kolkata Baharagora Amravati Durg Raipur 2 4 Tileibani Nagpur Bhilai Khambale Jalna Karanja 4 2 4 2 4 2 2 4 Sultanpur2 Sonewadi 2 4 Mumbai Legend Lane Length2 (km, %) 2 Lane 798 45% 4 Lane 1,013 55% Later Phases of NHDP were taken up as projects, leading to inconsistent infrastructure in corridors 4 Components of Bharatmala Pariyojana National Corridors Lane expansion, de-congestion of existing National Efficiency Improvement Corridors (GQ, NS-EW) Economic Corridors Connection of economically important production & development consumption centers; 44 corridors identified Inter-corridor and Feeder Inter-connection between different economic corridors, routes development development of first mile & last mile connectivity Coastal and Port Connectivity to coastal areas to enable port-led economic Connectivity Roads development & coastal tourism Border and International Connectivity to border areas & trade points with neighboring Connectivity Roads countries(Nepal, Bhutan, Bangladesh, Myanmar) Expressways Greenfield expressways (high density -

Inland Water Transport in NER By
Presentation on Inland Water Transport in NER By Inland Waterways Authority of India (Ministry of Shipping, Road Transport & Highways) Guwahati, the 9th March 2007 SADIYA Subansiri Hydel project SAIKHOWA Digboi refinery JAMGURI DIBRUGARH BOGIBIL TEJPUR Bongaigon refinery NEAMATI Numaligarh refinery JOGIGHOPA SILGHAT Legend Guwahati refinery DHUBRI Declared waterway (SHISHUMARA) PANDU BANGLADESH River distance B.Border (Dhubri) – Guwahati 260 km BANGLADESH Guwahati - Dibrugarh 508 km Dibrugarh– Sadiya 123 km Total length 891 km 1 North Bank South Bank Subanasiri Noa dihang Burali Burhi dihang Bargang Disang SADIYA Dhansiri Dikhu Puthimari Jhanju SAIKHOWA Pagladiya Dhansiri DIBRUGARH Beki Kopili Manas Kulsi BOGIBIL Aie Krishnai JAMGURI Champamati Jinary Gadadhar TEJPUR SILGHAT R. RA PUT HMA JOGIGHOPA BRA GUWAHATI DHUBRI PANDU H B A N G L A D SHISHUMARA E S Barak Valley Bhanga Badarpur Silchar 2 Objective Freight transportation by IWT to rise from the present level of 0.03 btkm to 5 btkm by 2025 Importance of IWT for NER z IWT offers shorter route compared to Road/rail z IWT operational even during flood season z Best suited for bulk commodities & Project cargo/ODC- z Provides best and low cost connectivity to hinterland z Employment potential enormous (NCAER Study Feb 2006) every km of IWT operation generates about 3000 jobs 1 lakh investment in IWT results in 6.5 manyears while in rail 0.58 and in other modes 0.87 manyears 3 Importance of IWT for NER Therefore, z Development of IWT mode in NER a strategic & economic imperative z Need for an investment & development strategy z Also need for increasing the efficiency of IWT mode. -

Capacity Building Workshop on Strenthening Transport
&$3$&,7<%8,/',1*:25.6+2321 675(17+(1,1*75$163257&211(&7,9,7< $021*&/097&28175,(6 '$7(7+ 2&72%(5 0,1,675<2)52$'75$163257$1'+,*+:$<6 1$7,21$/+,*+:$<6$1',1)5$6758&785( '(9(/230(17&25325$7,21/,0,7(' *29(510(172),1',$ &$3$&,7<%8,/',1*:25.6+2321 675(17+(1,1*75$163257&211(&7,9,7< $021*&/097&28175,(6 52$'6&211(&7,1*,1',$:,7+&/09± 7 &28175,(6 | ,1',$± 0<$10$5± 7+$,/$1' $6,$1+,*+:$<± , ¾ 7+( +,*+:$< 81'(5 &216758&7,21 81'(5 ,1',$¶6 /22. ($67 32/,&< 7+$7 :,// &211(&7 025(+ ,1',$ :,7+ 0$( 627 7+$,/$1' 9,$ 0<$10$5 7+( 21/< $6($1 &28175< 7+$7 6+$5(6 /$1' %25'(5 :,7+ ,1',$ :,7+ %,//,21 75$'( ¾ ,03+$/ ± 0$1'$/$< ± %$1*.2. &216,676 2) ,03+$/ 0$1'$/$< .0 $1' 0$1'$/$< %$1*.2. .0 727$/ /(1*7+ ± .0 ¾ .0 /21* <$*<, ± .$/(:$ 675(7&+ %(,1* 83*5$'(' 72 /$1( +,*+:$< %< ,1',$ ¾ 7+( 56 &525( 352-(&7 +$6 %((1 )81'(' %< ,1',$¶6 0,1,675< 2) (;7(51$/ $))$,56 ¾ ,1',$ +$6 $/5($'< %8,/7 7+( .0 6(&7,21 5()(55(' 72 $6 )5,(1'6+,3 +,*+:$< )520 7+( %25'(5 72:1 2) 7$08 72 .$/(:$ $ 6(3$5$7( &2175$&7 ,6 81'(5:$< )25 83*5$'$7,21 2) %5,'*(6 $/21* 7+( 7$08.$/(:$ 675(7&+ ¾ ,1',$ 3/$16 72 (;7(1' 52$' &211(&7,9,7< 72 7+( (17,5( &/09 &$0%2',$ /$26 0<$10$5 $1' 9,(71$0 5(*,21 52$'6&211(&7,1*,1',$:,7+&/09± 7 &28175,(6 | <$*<, .$/(:$6(&7,212)75,/$7(5$/+,*+:$< ¾ 7+,6 352-(&7 ,6 3$57 2) ,1',$1 ± 0<$10$5 ± 7+$,/$1' 75,/$7(5$/ +,*+:$< 0,1,675< 2) (;7(51$/ $))$,56 0($ +$6 (0%$5.(' 8321 $ 352*5$0 )25 &216758&7,21 7+528*+ 1$7,21$/ +,*+:$< $87+25,7< 2) ,1',$ ¾ 7+( 352-(&7 ,6 7+( '(9(/230(17 2) (;,67,1* .0 2) +,*+:$< 7:2 /$1( :,7+ ($57+(1 6+28/'(5 &21),*85$7,21 &211(&7,1* <$*<, 72 .$/(:$ -

2022 Brahmaputra River Cruise with Darjeeling
Brahmaputra River Cruise with Darjeeling, India Train rides, tea gardens and the mighty Brahmaputra River. Group departures See overleaf for departure dates Holiday overview Style Adventure Cruising Accommodation Hotels, Luxury Cruise Boat Grade Tour Duration 17 days from London to London Min/Max group size 2 / 12. Guaranteed to run for 2 Trip Leader Local Station & River Cruise Guides Land only Joining in Kolkata (Calcutta), India Max altitude 2,590m/8,497ft, Tiger Hill, Darjeeling, Day 5 Private Departures & Tailor Made itineraries available Watch related videos online: Brahmaputra River Cruise tel: +44 (0)1453 844400 fax: +44 (0)1453 844422 [email protected] www.mountainkingdoms.com Mountain Kingdoms Ltd, 20 Long Street, Wotton-under-Edge, Gloucestershire GL12 7BT UK Managing Director: Steven Berry. Registered in England No. 2118433. VAT No. 496 6511 08 Last updated: 11 May 2021 Departures Group departures 2022 Dates: Sat 26 Feb - Mon 14 Mar Sat 08 Oct – Mon 24 Oct 2023 Dates: Sat 25 Feb – Mon 13 Mar Deposit and payments A higher deposit is required to secure your booking on this holiday and your final balance is due 95 days before departure. For full details please contact the office or refer to our terms and conditions on our website http://www.mountainkingdoms.com/essential-information. Group prices and optional supplements Please contact us on +44 (0)1453 844400 or visit our website for our land only and flight inclusive prices and single supplement options. Single cabins: If you are travelling on your own and are willing to share, we will attempt to pair you up with another solo, same sex traveller.Where this is not possible a resulting single cabin has to be paid for. -

Playing to Strengths a Policy Framework for Mainstreaming Northeast India
Playing to Strengths Playing to Playing to Strengths A Policy Framework for Mainstreaming Northeast India Kathuria and Mathur Sanjay Kathuria and Priya Mathur, Editors INTERNATIONAL DEVELOPMENT IN FOCUS INTERNATIONAL INTERNATIONAL DEVELOPMENT IN FOCUS Playing to Strengths A Policy Framework for Mainstreaming Northeast India SANJAY KATHURIA AND PRIYA MATHUR, EDITORS © 2020 International Bank for Reconstruction and Development / The World Bank 1818 H Street NW, Washington, DC 20433 Telephone: 202-473-1000; Internet: www.worldbank.org Some rights reserved 1 2 3 4 22 21 20 19 Books in this series are published to communicate the results of Bank research, analysis, and operational experience with the least possible delay. The extent of language editing varies from book to book. This work is a product of the staff of The World Bank with external contributions. The findings, inter- pretations, and conclusions expressed in this work do not necessarily reflect the views of The World Bank, its Board of Executive Directors, or the governments they represent. The World Bank does not guarantee the accuracy of the data included in this work. The boundaries, colors, denominations, and other informa- tion shown on any map in this work do not imply any judgment on the part of The World Bank concerning the legal status of any territory or the endorsement or acceptance of such boundaries. Nothing herein shall constitute or be considered to be a limitation upon or waiver of the privileges and immunities of The World Bank, all of which are specifically reserved. Rights and Permissions This work is available under the Creative Commons Attribution 3.0 IGO license (CC BY 3.0 IGO) http:// creativecommons.org/licenses/by/3.0/igo.