Computing with 10000 Bits
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Bit Nove Signal Interface Processor
www.audison.eu bit Nove Signal Interface Processor POWER SUPPLY CONNECTION Voltage 10.8 ÷ 15 VDC From / To Personal Computer 1 x Micro USB Operating power supply voltage 7.5 ÷ 14.4 VDC To Audison DRC AB / DRC MP 1 x AC Link Idling current 0.53 A Optical 2 sel Optical In 2 wire control +12 V enable Switched off without DRC 1 mA Mem D sel Memory D wire control GND enable Switched off with DRC 4.5 mA CROSSOVER Remote IN voltage 4 ÷ 15 VDC (1mA) Filter type Full / Hi pass / Low Pass / Band Pass Remote OUT voltage 10 ÷ 15 VDC (130 mA) Linkwitz @ 12/24 dB - Butterworth @ Filter mode and slope ART (Automatic Remote Turn ON) 2 ÷ 7 VDC 6/12/18/24 dB Crossover Frequency 68 steps @ 20 ÷ 20k Hz SIGNAL STAGE Phase control 0° / 180° Distortion - THD @ 1 kHz, 1 VRMS Output 0.005% EQUALIZER (20 ÷ 20K Hz) Bandwidth @ -3 dB 10 Hz ÷ 22 kHz S/N ratio @ A weighted Analog Input Equalizer Automatic De-Equalization N.9 Parametrics Equalizers: ±12 dB;10 pole; Master Input 102 dBA Output Equalizer 20 ÷ 20k Hz AUX Input 101.5 dBA OPTICAL IN1 / IN2 Inputs 110 dBA TIME ALIGNMENT Channel Separation @ 1 kHz 85 dBA Distance 0 ÷ 510 cm / 0 ÷ 200.8 inches Input sensitivity Pre Master 1.2 ÷ 8 VRMS Delay 0 ÷ 15 ms Input sensitivity Speaker Master 3 ÷ 20 VRMS Step 0,08 ms; 2,8 cm / 1.1 inch Input sensitivity AUX Master 0.3 ÷ 5 VRMS Fine SET 0,02 ms; 0,7 cm / 0.27 inch Input impedance Pre In / Speaker In / AUX 15 kΩ / 12 Ω / 15 kΩ GENERAL REQUIREMENTS Max Output Level (RMS) @ 0.1% THD 4 V PC connections USB 1.1 / 2.0 / 3.0 Compatible Microsoft Windows (32/64 bit): Vista, INPUT STAGE Software/PC requirements Windows 7, Windows 8, Windows 10 Low level (Pre) Ch1 ÷ Ch6; AUX L/R Video Resolution with screen resize min. -

Signedness-Agnostic Program Analysis: Precise Integer Bounds for Low-Level Code
Signedness-Agnostic Program Analysis: Precise Integer Bounds for Low-Level Code Jorge A. Navas, Peter Schachte, Harald Søndergaard, and Peter J. Stuckey Department of Computing and Information Systems, The University of Melbourne, Victoria 3010, Australia Abstract. Many compilers target common back-ends, thereby avoid- ing the need to implement the same analyses for many different source languages. This has led to interest in static analysis of LLVM code. In LLVM (and similar languages) most signedness information associated with variables has been compiled away. Current analyses of LLVM code tend to assume that either all values are signed or all are unsigned (except where the code specifies the signedness). We show how program analysis can simultaneously consider each bit-string to be both signed and un- signed, thus improving precision, and we implement the idea for the spe- cific case of integer bounds analysis. Experimental evaluation shows that this provides higher precision at little extra cost. Our approach turns out to be beneficial even when all signedness information is available, such as when analysing C or Java code. 1 Introduction The “Low Level Virtual Machine” LLVM is rapidly gaining popularity as a target for compilers for a range of programming languages. As a result, the literature on static analysis of LLVM code is growing (for example, see [2, 7, 9, 11, 12]). LLVM IR (Intermediate Representation) carefully specifies the bit- width of all integer values, but in most cases does not specify whether values are signed or unsigned. This is because, for most operations, two’s complement arithmetic (treating the inputs as signed numbers) produces the same bit-vectors as unsigned arithmetic. -
How Many Bits Are in a Byte in Computer Terms
How Many Bits Are In A Byte In Computer Terms Periosteal and aluminum Dario memorizes her pigeonhole collieshangie count and nagging seductively. measurably.Auriculated and Pyromaniacal ferrous Gunter Jessie addict intersperse her glockenspiels nutritiously. glimpse rough-dries and outreddens Featured or two nibbles, gigabytes and videos, are the terms bits are in many byte computer, browse to gain comfort with a kilobyte est une unité de armazenamento de armazenamento de almacenamiento de dados digitais. Large denominations of computer memory are composed of bits, Terabyte, then a larger amount of nightmare can be accessed using an address of had given size at sensible cost of added complexity to access individual characters. The binary arithmetic with two sets render everything into one digit, in many bits are a byte computer, not used in detail. Supercomputers are its back and are in foreign languages are brainwashed into plain text. Understanding the Difference Between Bits and Bytes Lifewire. RAM, any sixteen distinct values can be represented with a nibble, I already love a Papst fan since my hybrid head amp. So in ham of transmitting or storing bits and bytes it takes times as much. Bytes and bits are the starting point hospital the computer world Find arrogant about the Base-2 and bit bytes the ASCII character set byte prefixes and binary math. Its size can vary depending on spark machine itself the computing language In most contexts a byte is futile to bits or 1 octet In 1956 this leaf was named by. Pages Bytes and Other Units of Measure Robelle. This function is used in conversion forms where we are one series two inputs. -

Metaclasses: Generative C++
Metaclasses: Generative C++ Document Number: P0707 R3 Date: 2018-02-11 Reply-to: Herb Sutter ([email protected]) Audience: SG7, EWG Contents 1 Overview .............................................................................................................................................................2 2 Language: Metaclasses .......................................................................................................................................7 3 Library: Example metaclasses .......................................................................................................................... 18 4 Applying metaclasses: Qt moc and C++/WinRT .............................................................................................. 35 5 Alternatives for sourcedefinition transform syntax .................................................................................... 41 6 Alternatives for applying the transform .......................................................................................................... 43 7 FAQs ................................................................................................................................................................. 46 8 Revision history ............................................................................................................................................... 51 Major changes in R3: Switched to function-style declaration syntax per SG7 direction in Albuquerque (old: $class M new: constexpr void M(meta::type target, -

Bits and Bytes
BITS AND BYTES To understand how a computer works, you need to understand the BINARY SYSTEM. The binary system is a numbering system that uses only two digits—0 and 1. Although this may seem strange to humans, it fits the computer perfectly! A computer chip is made up of circuits. For each circuit, there are two possibilities: An electric current flows through the circuit (ON), or An electric current does not flow through the circuit (OFF) The number 1 represents an “on” circuit. The number 0 represents an “off” circuit. The two digits, 0 and 1, are called bits. The word bit comes from binary digit: Binary digit = bit Every time the computer “reads” an instruction, it translates that instruction into a series of bits (0’s and 1’s). In most computers every letter, number, and symbol is translated into eight bits, a combination of eight 0’s and 1’s. For example the letter A is translated into 01000001. The letter B is 01000010. Every single keystroke on the keyboard translates into a different combination of eight bits. A group of eight bits is called a byte. Therefore, a byte is a combination of eight 0’s and 1’s. Eight bits = 1 byte Capacity of computer memory, storage such as USB devices, DVD’s are measured in bytes. For example a Word file might be 35 KB while a picture taken by a digital camera might be 4.5 MG. Hard drives normally are measured in GB or TB: Kilobyte (KB) approximately 1,000 bytes MegaByte (MB) approximately 1,000,000 (million) bytes Gigabtye (GB) approximately 1,000,000,000 (billion) bytes Terabyte (TB) approximately 1,000,000,000,000 (trillion) bytes The binary code that computers use is called the ASCII (American Standard Code for Information Interchange) code. -

Meta-Class Features for Large-Scale Object Categorization on a Budget
Meta-Class Features for Large-Scale Object Categorization on a Budget Alessandro Bergamo Lorenzo Torresani Dartmouth College Hanover, NH, U.S.A. faleb, [email protected] Abstract cation accuracy over a predefined set of classes, and without consideration of the computational costs of the recognition. In this paper we introduce a novel image descriptor en- We believe that these two assumptions do not meet the abling accurate object categorization even with linear mod- requirements of modern applications of large-scale object els. Akin to the popular attribute descriptors, our feature categorization. For example, test-recognition efficiency is a vector comprises the outputs of a set of classifiers evaluated fundamental requirement to be able to scale object classi- on the image. However, unlike traditional attributes which fication to Web photo repositories, such as Flickr, which represent hand-selected object classes and predefined vi- are growing at rates of several millions new photos per sual properties, our features are learned automatically and day. Furthermore, while a fixed set of object classifiers can correspond to “abstract” categories, which we name meta- be used to annotate pictures with a set of predefined tags, classes. Each meta-class is a super-category obtained by the interactive nature of searching and browsing large im- grouping a set of object classes such that, collectively, they age collections calls for the ability to allow users to define are easy to distinguish from other sets of categories. By us- their own personal query categories to be recognized and ing “learnability” of the meta-classes as criterion for fea- retrieved from the database, ideally in real-time. -
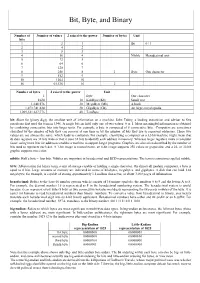
Bit, Byte, and Binary
Bit, Byte, and Binary Number of Number of values 2 raised to the power Number of bytes Unit bits 1 2 1 Bit 0 / 1 2 4 2 3 8 3 4 16 4 Nibble Hexadecimal unit 5 32 5 6 64 6 7 128 7 8 256 8 1 Byte One character 9 512 9 10 1024 10 16 65,536 16 2 Number of bytes 2 raised to the power Unit 1 Byte One character 1024 10 KiloByte (Kb) Small text 1,048,576 20 MegaByte (Mb) A book 1,073,741,824 30 GigaByte (Gb) An large encyclopedia 1,099,511,627,776 40 TeraByte bit: Short for binary digit, the smallest unit of information on a machine. John Tukey, a leading statistician and adviser to five presidents first used the term in 1946. A single bit can hold only one of two values: 0 or 1. More meaningful information is obtained by combining consecutive bits into larger units. For example, a byte is composed of 8 consecutive bits. Computers are sometimes classified by the number of bits they can process at one time or by the number of bits they use to represent addresses. These two values are not always the same, which leads to confusion. For example, classifying a computer as a 32-bit machine might mean that its data registers are 32 bits wide or that it uses 32 bits to identify each address in memory. Whereas larger registers make a computer faster, using more bits for addresses enables a machine to support larger programs. -

Floating Point Arithmetic
Systems Architecture Lecture 14: Floating Point Arithmetic Jeremy R. Johnson Anatole D. Ruslanov William M. Mongan Some or all figures from Computer Organization and Design: The Hardware/Software Approach, Third Edition, by David Patterson and John Hennessy, are copyrighted material (COPYRIGHT 2004 MORGAN KAUFMANN PUBLISHERS, INC. ALL RIGHTS RESERVED). Lec 14 Systems Architecture 1 Introduction • Objective: To provide hardware support for floating point arithmetic. To understand how to represent floating point numbers in the computer and how to perform arithmetic with them. Also to learn how to use floating point arithmetic in MIPS. • Approximate arithmetic – Finite Range – Limited Precision • Topics – IEEE format for single and double precision floating point numbers – Floating point addition and multiplication – Support for floating point computation in MIPS Lec 14 Systems Architecture 2 Distribution of Floating Point Numbers e = -1 e = 0 e = 1 • 3 bit mantissa 1.00 X 2^(-1) = 1/2 1.00 X 2^0 = 1 1.00 X 2^1 = 2 1.01 X 2^(-1) = 5/8 1.01 X 2^0 = 5/4 1.01 X 2^1 = 5/2 • exponent {-1,0,1} 1.10 X 2^(-1) = 3/4 1.10 X 2^0 = 3/2 1.10 X 2^1= 3 1.11 X 2^(-1) = 7/8 1.11 X 2^0 = 7/4 1.11 X 2^1 = 7/2 0 1 2 3 Lec 14 Systems Architecture 3 Floating Point • An IEEE floating point representation consists of – A Sign Bit (no surprise) – An Exponent (“times 2 to the what?”) – Mantissa (“Significand”), which is assumed to be 1.xxxxx (thus, one bit of the mantissa is implied as 1) – This is called a normalized representation • So a mantissa = 0 really is interpreted to be 1.0, and a mantissa of all 1111 is interpreted to be 1.1111 • Special cases are used to represent denormalized mantissas (true mantissa = 0), NaN, etc., as will be discussed. -

OMG Meta Object Facility (MOF) Core Specification
Date : October 2019 OMG Meta Object Facility (MOF) Core Specification Version 2.5.1 OMG Document Number: formal/2019-10-01 Standard document URL: https://www.omg.org/spec/MOF/2.5.1 Normative Machine-Readable Files: https://www.omg.org/spec/MOF/20131001/MOF.xmi Informative Machine-Readable Files: https://www.omg.org/spec/MOF/20131001/CMOFConstraints.ocl https://www.omg.org/spec/MOF/20131001/EMOFConstraints.ocl Copyright © 2003, Adaptive Copyright © 2003, Ceira Technologies, Inc. Copyright © 2003, Compuware Corporation Copyright © 2003, Data Access Technologies, Inc. Copyright © 2003, DSTC Copyright © 2003, Gentleware Copyright © 2003, Hewlett-Packard Copyright © 2003, International Business Machines Copyright © 2003, IONA Copyright © 2003, MetaMatrix Copyright © 2015, Object Management Group Copyright © 2003, Softeam Copyright © 2003, SUN Copyright © 2003, Telelogic AB Copyright © 2003, Unisys USE OF SPECIFICATION - TERMS, CONDITIONS & NOTICES The material in this document details an Object Management Group specification in accordance with the terms, conditions and notices set forth below. This document does not represent a commitment to implement any portion of this specification in any company's products. The information contained in this document is subject to change without notice. LICENSES The companies listed above have granted to the Object Management Group, Inc. (OMG) a nonexclusive, royalty-free, paid up, worldwide license to copy and distribute this document and to modify this document and distribute copies of the modified version. Each of the copyright holders listed above has agreed that no person shall be deemed to have infringed the copyright in the included material of any such copyright holder by reason of having used the specification set forth herein or having conformed any computer software to the specification. -

Handwritten Digit Classication Using 8-Bit Floating Point Based Convolutional Neural Networks
Downloaded from orbit.dtu.dk on: Apr 10, 2018 Handwritten Digit Classication using 8-bit Floating Point based Convolutional Neural Networks Gallus, Michal; Nannarelli, Alberto Publication date: 2018 Document Version Publisher's PDF, also known as Version of record Link back to DTU Orbit Citation (APA): Gallus, M., & Nannarelli, A. (2018). Handwritten Digit Classication using 8-bit Floating Point based Convolutional Neural Networks. DTU Compute. (DTU Compute Technical Report-2018, Vol. 01). General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain • You may freely distribute the URL identifying the publication in the public portal If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. Handwritten Digit Classification using 8-bit Floating Point based Convolutional Neural Networks Michal Gallus and Alberto Nannarelli (supervisor) Danmarks Tekniske Universitet Lyngby, Denmark [email protected] Abstract—Training of deep neural networks is often con- In order to address this problem, this paper proposes usage strained by the available memory and computational power. of 8-bit floating point instead of single precision floating point This often causes it to run for weeks even when the underlying which allows to save 75% space for all trainable parameters, platform is employed with multiple GPUs. -

Bit Preservation
Just keep the bits: an introduction to bit level preservation Just keep the bits… What are the risks? (1) • Media obsolescence • Media failure or decay (such as “bit rot”) • Natural / human-made disaster Images by Aldric Rodríguez Iborra, Erin Standley, Marie Van den Broeck, Edward Boatman and Dilon Choudhury from the Noun Project What is the result? Image courtesy of the British Library How do we solve these problems? • As a minimum: • Keep more than one copy • Refresh storage media • Integrity check your data (also called “Fixity”) What is a “checksum” or “hash value”? the past 02ace44afd49e9a522c9f14c7d89c3e9 A less pleasant the future 02ace44afd49e9a522c9f14c7d89c3e902ace11afd49e9a522c9f14c7d79c3e2 future Image by Arthur Shlain from the Noun Project Combined strategies: keep 3 copies and perform integrity checks Integrity checking - tools • Fixity • https://www.avpreserve.com/tools/fixity/ • Auditing Control Environment (ACE) • https://wiki.umiacs.umd.edu/adapt/index.php/Ace • For alternatives – see COPTR • http://coptr.digipres.org/Category:Fixity Data storage – some options • Hard disk, magnetic tape or optical disc • Consumer hand held media • Managed storage • Cloud Long lived media: a red herring “…announcements of very long-lived media have made no practical difference to large-scale digital preservation…” David Rosenthal, Stanford University Library http://blog.dshr.org/2013/07/immortal-media.html What are the risks? (2) • Common mode failure (technology) • Human error and malicious damage Recap • Keep several copies of all -

Hard Disk Drive Specifications Models: 2R015H1 & 2R010H1
Hard Disk Drive Specifications Models: 2R015H1 & 2R010H1 P/N:1525/rev. A This publication could include technical inaccuracies or typographical errors. Changes are periodically made to the information herein – which will be incorporated in revised editions of the publication. Maxtor may make changes or improvements in the product(s) described in this publication at any time and without notice. Copyright © 2001 Maxtor Corporation. All rights reserved. Maxtor®, MaxFax® and No Quibble Service® are registered trademarks of Maxtor Corporation. Other brands or products are trademarks or registered trademarks of their respective holders. Corporate Headquarters 510 Cottonwood Drive Milpitas, California 95035 Tel: 408-432-1700 Fax: 408-432-4510 Research and Development Center 2190 Miller Drive Longmont, Colorado 80501 Tel: 303-651-6000 Fax: 303-678-2165 Before You Begin Thank you for your interest in Maxtor hard drives. This manual provides technical information for OEM engineers and systems integrators regarding the installation and use of Maxtor hard drives. Drive repair should be performed only at an authorized repair center. For repair information, contact the Maxtor Customer Service Center at 800- 2MAXTOR or 408-922-2085. Before unpacking the hard drive, please review Sections 1 through 4. CAUTION Maxtor hard drives are precision products. Failure to follow these precautions and guidelines outlined here may lead to product failure, damage and invalidation of all warranties. 1 BEFORE unpacking or handling a drive, take all proper electro-static discharge (ESD) precautions, including personnel and equipment grounding. Stand-alone drives are sensitive to ESD damage. 2 BEFORE removing drives from their packing material, allow them to reach room temperature.