DOCSLIB.ORG

Table Look-Up CORDIC: Effective Rotations Through Angle Partitioning

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Table Look-Up CORDIC: Effective Rotations Through Angle Partitioning Copyright by Jason Todd Arbaugh 2004 The Dissertation Committee for Jason Todd Arbaugh certifies that this is the approved version of the following dissertation: Table Look -up CORDIC: Effective Rotations Through Angle Partitioning Committee: ______________________________ Earl E. Swartzlander, Jr., Supervisor ______________________________ Anthony P. Ambler ______________________________ John H. Davis ______________________________ Chang Yong Kang ______________________________ Nur A. To uba Table Look -up CORDIC: Effective Rotations Through Angle Partitioning by Jason Todd Arbaugh, B.S., M.S. Dissertation Presented to the Faculty of the Graduate School of the University of Texas at Austin in Partial Fulfillment of the Requirements for the degree of Doctor of Philosophy The University of Texas at Austin December 2004 This dissertation is dedicated to all of the teachers in my life: those who have taught me theory in my classrooms, application in my jobs in industry, hard wo rk in my activities, integrity in my interactions, and balance in my life. Acknowledgements There are many people that deserve acknowledgement for their help in completing this dissertation. The help they provided, while not always technical in nature, was sorely needed at various times during my research, implementation, writing, and editing. I would like to thank Dr. Earl E. Swartzlander, Jr. for all of his teaching, help, and encouragement in graduate school. From his class on High Speed Arithmetic to his advice as my supervisor, I have enjoyed his humor, imagination, knowledge, and support. I have, and will continue to appreciate his mentorship. And even when he insists that I call him Earl, I will always regard him as Dr. Swartzlander. I am also thankful to the members of my dissertation committee Dr. Tony Ambler, Dr. John Davis, Dr. Chang Yong Kang, and Dr. Nur Touba. In addition to their time, which is so very valuable in today’s hectic world, they have provided valuable insights and timely sug gestions that have widened the scope and improved the content and quality of my dissertation. Brian P. Klawinski, Esquire, provided seemingly instantaneous assistance in the development of several of the C++ programs used in the calculation, evaluation, an d verification of the Table Look-up CORDIC algorithm. Mr. Paul T. Muehr helped with the setup of the backend tools. Without his help with the environment, scripts for the synthesis, auto place and route, and static timing analysis of my Verilog, I would not have been able to meet my deadlines. In addition to my committee and supervisor, Mr. Charles Pummill and Mrs. Sherri Staley assisted in reading, critiquing, and improving this dissertation. Their help on my dissertation has been greatly appreciated. My close friend, Mr. Chris W. Mobley, helped keep me motivated and healthy through the many long days of sitting in front of the computer typing. The v games of racquetball, the workouts, the pep talks, the reality checks, and the social interaction have kept me from going completely insane. I would like to thank Dr. Dhananjay Phatak, Associate Professor at the University of Maryland, Baltimore County, for providing my a copy of some of the C code used in simulating his Double Step Branching CORDIC algorithm. The C code was very helpful for figuring out some of the nuances of the algorithm that were not covered in the published paper. And finally, I would like to thank my entire family for helping make me who I am today: my mother and father, Sherri E. Staley and Wayne L. Arbaugh, my stepparents, Dr. Leo G. Staley and Kathy Arbaugh, my brothers and step -sister, “Huck” Fenn J. Arbaugh, Dr. Jesse L. Arbaugh, and Kristi Bogans. vi Table Look -up CORDIC: Effective Rotations Through Angle Partitioning Publication No . ___________________ Jason Todd Arbaugh, Ph.D. The University of Texas at Austin, 2004 Supervisor: Earl E. Swartzlander, Jr. This dissertation documents the development, derivation, verification, implementation, and evaluation of an improved versio n of the COordinate Rotation DIgital Computer (CORDIC) algorithm for calculating sine and cosine values. The CORDIC algorithm was originally developed to calculate trigonometric relationships in navigation systems using a family of linearly converging ite ration equations. The CORDIC algorithm computes numerous elementary functions including powers, exponentials, logarithms, trigonometric and hyperbolic functions. Many different versions of the classic CORDIC algorithm have been developed to enhance the performance of calculating these elementary functions. These alternative algorithms utilize methods that vary from using different number systems, to increasing the number of rotations performed in each iteration, to calculating the rotations using differen t Arc Tangent Radices. Even though each of vii these methods improves the performance of the CORDIC calculations, they still require a significant number of iterations through the CORDIC equations to obtain the final answer. The new CORDIC algorithm utilizes look-up tables and standard microprocessor arithmetic functional units to perform the calculations. The look-up tables employ either the traditional CORDIC or the new Parallel Arc Tangent Radix (ATR). The traditional CORDIC ATR combines multiple CORDIC iterations into a single effective rotation. The parallel ATR uses the exact angle value to perform the rotation rather than a summation of CORDIC ATR angles. Utilizing exact angles reduces the complexity of the decoders and permits parallel access to th e ROMs. The Table Look-up CORDIC (TLC) algorithm is shown to be correct through the development of a mathematical proof utilizing the polar form of the CORDIC iteration equations. The TLC algorithm and other versions of the CORDIC algorithm are implemente d in MatLab and simulated. The results of these simulations are compared with the bit correct value calculated with MatLab’s built in trigonometric functions to verify the correct operation. The same CORDIC algorithms are then modeled in Verilog. The Ver ilog models are synthesized to gates, placed and routed, and statically timed. The auto place and route of these circuits allows area estimates to be obtained for the different algorithms. The static timing analysis allows the worst -case path to be timed for frequency and latency comparisons. viii Table of Contents List of Tables ............................................................................................................. xii List of Figures ........................................................................................................... xiv List of Supplemental Files ........................................................................................ xvi Chapter 1 Introduction .................................................................................................1 1.1 Elementary Functions .................................................................................. 1 1.2 Previous Research ........................................................................................ 3 1.3 Table Look-up CORDIC .............................................................................. 6 Chapter 2 Algorithm Classes ....................................................................................... 8 2.1 Polynomial Approximation.......................................................................... 8 2.2 Rational Approximation............................................................................. 10 2.3 Linear Convergence ................................................................................... 13 2.4 Quadratic Convergence .............................................................................. 14 2.5 Research Opportunities .............................................................................. 16 Chapter 3 Classic CORDIC Algorithm...................................................................... 18 3.1 The Unit Circle .......................................................................................... 19 3.2 Calculation by Rotation ............................................................................. 21 3.3 Angle Selection.......................................................................................... 26 3.4 Rotation Direction...................................................................................... 28 3.5 Scale Factor................................................................................................ 28 3.6 Angle Criteria ............................................................................................. 29 3.7 Iteration Equations..................................................................................... 30 3.8 Pseudo Rotations........................................................................................ 31 Chapter 4 Previous Work ........................................................................................... 32 4.1 Unified CORDIC ....................................................................................... 33 4.2 Step -Branching CORDIC .......................................................................... 34 4.3 Double Step -Branching CORDIC .............................................................. 37 ix 4.4 Hybrid CORDIC ........................................................................................ 40 Chapter 5 Table Look-up CORDIC Algorit hm ......................................................... 42 5.1 Effective Rotations....................................................................................
Load more

Recommended publications
  • Comparison of Parallel and Pipelined CORDIC Algorithm Using RCA and CSA
    Comparison of Parallel and Pipelined CORDIC algorithm using RCA and CSA Diego Barragan´ Guerrero Lu´ıs Geraldo P. Meloni FEEC - UNICAMP FEEC - UNICAMP Campinas, Sao˜ Paulo, Brazil, 13083-852 Campinas, Sao˜ Paulo, Brazil, 13083-852 +5519 9308-9952 +5519 9778-1523 [email protected] [email protected] Abstract— This paper presents an implementation of the algorithm has two modes of operation: the rotational mode CORDIC algorithm in digital hardware using two types of (RM) where the vector (xi; yi) is rotated by an angle θ to algebraic adders: Ripple-Carry Adder (RCA) and Carry-Select obtain a new vector (x ; y ), and the vectoring mode (VM) Adder (CSA), both in parallel and pipelined architectures. Anal- N N ysis of time performance and resources utilization was carried in which the algorithm computes the modulus R and phase α out by changing the algorithm number of iterations. These results from the x-axis of the vector (x0; y0). The basic principle of demonstrate the efficiency in operating frequency of the pipelined the algorithm is shown in Figure 1. architecture with respect to the parallel architecture. Also it is shown that the use of CSA reduce the timing processing without significantly increasing the slice use. The code was synthesized us- ing FPGA development tools for the Xilinx Spartan-3E xc3s500e ' ' E N y family. N E N Index Terms— CORDIC, pipelined, parallel, RCA, CSA, y N trigonometrics functions. Rotação Pseudo-rotação R N I. INTRODUCTION E i In Digital Signal Processing with FPGA, trigonometric y i R i functions are used in many signal algorithms, for instance N synchronization and equalization [12].
    [Show full text]
  • Basics of Logic Design Arithmetic Logic Unit (ALU) Today's Lecture
    Basics of Logic Design Arithmetic Logic Unit (ALU) CPS 104 Lecture 9 Today’s Lecture • Homework #3 Assigned Due March 3 • Project Groups assigned & posted to blackboard. • Project Specification is on Web Due April 19 • Building the building blocks… Outline • Review • Digital building blocks • An Arithmetic Logic Unit (ALU) Reading Appendix B, Chapter 3 © Alvin R. Lebeck CPS 104 2 Review: Digital Design • Logic Design, Switching Circuits, Digital Logic Recall: Everything is built from transistors • A transistor is a switch • It is either on or off • On or off can represent True or False Given a bunch of bits (0 or 1)… • Is this instruction a lw or a beq? • What register do I read? • How do I add two numbers? • Need a method to reason about complex expressions © Alvin R. Lebeck CPS 104 3 Review: Boolean Functions • Boolean functions have arguments that take two values ({T,F} or {0,1}) and they return a single or a set of ({T,F} or {0,1}) value(s). • Boolean functions can always be represented by a table called a “Truth Table” • Example: F: {0,1}3 -> {0,1}2 a b c f1f2 0 0 0 0 1 0 0 1 1 1 0 1 0 1 0 0 1 1 0 0 1 0 0 1 0 1 1 0 0 1 1 1 1 1 1 © Alvin R. Lebeck CPS 104 4 Review: Boolean Functions and Expressions F(A, B, C) = (A * B) + (~A * C) ABCF 0000 0011 0100 0111 1000 1010 1101 1111 © Alvin R. Lebeck CPS 104 5 Review: Boolean Gates • Gates are electronics devices that implement simple Boolean functions Examples a a AND(a,b) OR(a,b) a NOT(a) b b a XOR(a,b) a NAND(a,b) b b a NOR(a,b) a XNOR(a,b) b b © Alvin R.
    [Show full text]
  • Binary Counter
    Systems I: Computer Organization and Architecture Lecture 8: Registers and Counters Registers • A register is a group of flip-flops. – Each flip-flop stores one bit of data; n flip-flops are required to store n bits of data. – There are several different types of registers available commercially. – The simplest design is a register consisting only of flip- flops, with no other gates in the circuit. • Loading the register – transfer of new data into the register. • The flip-flops share a common clock pulse (frequently using a buffer to reduce power requirements). • Output could be sampled at any time. • Clearing the flip-flop (placing zeroes in all its bit) can be done through a special terminal on the flip-flop. 1 4-bit Register I0 D Q A0 Clock C I1 D Q A1 C I D Q 2 A2 C D Q A I3 3 C Clear Registers With Parallel Load • The clock usually provides a steady stream of pulses which are applied to all flip-flops in the system. • A separate control system is needed to determine when to load a particular register. • The Register with Parallel Load has a separate load input. – When it is cleared, the register receives it output as input. – When it is set, it received the load input. 2 4-bit Register With Parallel Load Load D Q A0 I0 C D Q A1 C I1 D Q A2 I2 C D Q A3 I3 C Clock Shift Registers • A shift register is a register which can shift its data in one or both directions.
    [Show full text]
  • Unit Circle Trigonometry
    UNIT CIRCLE TRIGONOMETRY The Unit Circle is the circle centered at the origin with radius 1 unit (hence, the “unit” circle). The equation of this circle is xy22+ =1. A diagram of the unit circle is shown below: y xy22+ = 1 1 x -2 -1 1 2 -1 -2 We have previously applied trigonometry to triangles that were drawn with no reference to any coordinate system. Because the radius of the unit circle is 1, we will see that it provides a convenient framework within which we can apply trigonometry to the coordinate plane. Drawing Angles in Standard Position We will first learn how angles are drawn within the coordinate plane. An angle is said to be in standard position if the vertex of the angle is at (0, 0) and the initial side of the angle lies along the positive x-axis. If the angle measure is positive, then the angle has been created by a counterclockwise rotation from the initial to the terminal side. If the angle measure is negative, then the angle has been created by a clockwise rotation from the initial to the terminal side. θ in standard position, where θ is positive: θ in standard position, where θ is negative: y y Terminal side θ Initial side x x Initial side θ Terminal side Unit Circle Trigonometry Drawing Angles in Standard Position Examples The following angles are drawn in standard position: y y 1. θ = 40D 2. θ =160D θ θ x x y 3. θ =−320D Notice that the terminal sides in examples 1 and 3 are in the same position, but they do not represent the same angle (because x the amount and direction of the rotation θ in each is different).
    [Show full text]
  • Cross Architectural Power Modelling
    Cross Architectural Power Modelling Kai Chen1, Peter Kilpatrick1, Dimitrios S. Nikolopoulos2, and Blesson Varghese1 1Queen’s University Belfast, UK; 2Virginia Tech, USA E-mail: [email protected]; [email protected]; [email protected]; [email protected] Abstract—Existing power modelling research focuses on the processor are extensively explored using a cumbersome trial model rather than the process for developing models. An auto- and error approach after which a suitable few are selected [7]. mated power modelling process that can be deployed on different Such an approach does not easily scale for various processor processors for developing power models with high accuracy is developed. For this, (i) an automated hardware performance architectures since a different set of hardware counters will be counter selection method that selects counters best correlated to required to model power for each processor. power on both ARM and Intel processors, (ii) a noise filter based Currently, there is little research that develops automated on clustering that can reduce the mean error in power models, and (iii) a two stage power model that surmounts challenges in methods for selecting hardware counters to capture proces- using existing power models across multiple architectures are sor power over multiple processor architectures. Automated proposed and developed. The key results are: (i) the automated methods are required for easily building power models for a hardware performance counter selection method achieves compa- collection of heterogeneous processors as seen in traditional rable selection to the manual method reported in the literature, data centers that host multiple generations of server proces- (ii) the noise filter reduces the mean error in power models by up to 55%, and (iii) the two stage power model can predict sors, or in emerging distributed computing environments like dynamic power with less than 8% error on both ARM and Intel fog/edge computing [8] and mobile cloud computing (in these processors, which is an improvement over classic models.
    [Show full text]
  • Implementation of Carry Tree Adders and Compare with RCA and CSLA
    International Journal of Emerging Engineering Research and Technology Volume 4, Issue 1, January 2016, PP 1-11 ISSN 2349-4395 (Print) & ISSN 2349-4409 (Online) Implementation of Carry Tree Adders and Compare with RCA and CSLA 1 2 G. Venkatanaga Kumar , C.H Pushpalatha Department of ECE, GONNA INSTITUTE OF TECHNOLOGY, Vishakhapatnam, India (PG Scholar) Department of ECE, GONNA INSTITUTE OF TECHNOLOGY, Vishakhapatnam, India (Associate Professor) ABSTRACT The binary adder is the critical element in most digital circuit designs including digital signal processors (DSP) and microprocessor data path units. As such, extensive research continues to be focused on improving the power delay performance of the adder. In VLSI implementations, parallel-prefix adders are known to have the best performance. Binary adders are one of the most essential logic elements within a digital system. In addition, binary adders are also helpful in units other than Arithmetic Logic Units (ALU), such as multipliers, dividers and memory addressing. Therefore, binary addition is essential that any improvement in binary addition can result in a performance boost for any computing system and, hence, help improve the performance of the entire system. Parallel-prefix adders (also known as carry-tree adders) are known to have the best performance in VLSI designs. This paper investigates three types of carry-tree adders (the Kogge- Stone, sparse Kogge-Stone, Ladner-Fischer and spanning tree adder) and compares them to the simple Ripple Carry Adder (RCA) and Carry Skip Adder (CSA). In this project Xilinx-ISE tool is used for simulation, logical verification, and further synthesizing. This algorithm is implemented in Xilinx 13.2 version and verified using Spartan 3e kit.
    [Show full text]
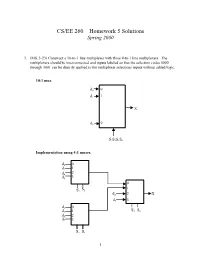
  • CS/EE 260 – Homework 5 Solutions Spring 2000
    CS/EE 260 – Homework 5 Solutions Spring 2000 1. (MK 3-23) Construct a 10-to-1 line multiplexer with three 4-to-1 line multiplexers. The multiplexers should be interconnected and inputs labeled so that the selection codes 0000 through 1001 can be directly applied to the multiplexer selections inputs without added logic. 10:1 mux d0 0 1 d1 1 X d9 9 S3S2S1S0 Implementation using 4:1 muxes. d0 0 d2 1 d4 2 d6 3 0 S 1 S2 1 d8 2 X d9 3 d 0 1 S S d3 1 3 0 d5 2 d7 3 S2 S1 1 2. (MK 3-27) Implement a binary full adder with a dual 4-to-1 line multiplexer and a single inverter. AB Ci S Co 00 0 0 0 C 0 00 1 1 i 0 01 0 1 0 C ´ C 01 1 0 i 1 i 10 0 1 0 10 1 0Ci´ 1 Ci 11 0 0 1 C 1 11 1 1 i 1 0 C 1 i 4:1 2 S 3 mux S1 S0 A B 0 0 1 4:1 Co 2 mux 1 3 S1S0 2 3. (MK 3-34) Design a combinational circuit that forms the 2-bit binary sum S1S0 of two 2-bit numbers A1A0 and B1B0 and has both input C0 and a carry output C2. Do not use half adders or full adders, but instead use a two-level circuit plus inverters for the input variables, as needed. Design the circuit by starting with the following equations for each of the two bits of the adder.
    [Show full text]
  • 3.2 the CORDIC Algorithm
    UC San Diego UC San Diego Electronic Theses and Dissertations Title Improved VLSI architecture for attitude determination computations Permalink https://escholarship.org/uc/item/5jf926fv Author Arrigo, Jeanette Fay Freauf Publication Date 2006 Peer reviewed|Thesis/dissertation eScholarship.org Powered by the California Digital Library University of California 1 UNIVERSITY OF CALIFORNIA, SAN DIEGO Improved VLSI Architecture for Attitude Determination Computations A dissertation submitted in partial satisfaction of the requirements for the degree Doctor of Philosophy in Electrical and Computer Engineering (Electronic Circuits and Systems) by Jeanette Fay Freauf Arrigo Committee in charge: Professor Paul M. Chau, Chair Professor C.K. Cheng Professor Sujit Dey Professor Lawrence Larson Professor Alan Schneider 2006 2 Copyright Jeanette Fay Freauf Arrigo, 2006 All rights reserved. iv DEDICATION This thesis is dedicated to my husband Dale Arrigo for his encouragement, support and model of perseverance, and to my father Eugene Freauf for his patience during my pursuit. In memory of my mother Fay Freauf and grandmother Fay Linton Thoreson, incredible mentors and great advocates of the quest for knowledge. iv v TABLE OF CONTENTS Signature Page...............................................................................................................iii Dedication … ................................................................................................................iv Table of Contents ...........................................................................................................v
    [Show full text]
  • CORDIC-Like Method for Solving Kepler's Equation
    A&A 619, A128 (2018) Astronomy https://doi.org/10.1051/0004-6361/201833162 & c ESO 2018 Astrophysics CORDIC-like method for solving Kepler’s equation M. Zechmeister Institut für Astrophysik, Georg-August-Universität, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany e-mail: [email protected] Received 4 April 2018 / Accepted 14 August 2018 ABSTRACT Context. Many algorithms to solve Kepler’s equations require the evaluation of trigonometric or root functions. Aims. We present an algorithm to compute the eccentric anomaly and even its cosine and sine terms without usage of other transcen- dental functions at run-time. With slight modifications it is also applicable for the hyperbolic case. Methods. Based on the idea of CORDIC, our method requires only additions and multiplications and a short table. The table is inde- pendent of eccentricity and can be hardcoded. Its length depends on the desired precision. Results. The code is short. The convergence is linear for all mean anomalies and eccentricities e (including e = 1). As a stand-alone algorithm, single and double precision is obtained with 29 and 55 iterations, respectively. Half or two-thirds of the iterations can be saved in combination with Newton’s or Halley’s method at the cost of one division. Key words. celestial mechanics – methods: numerical 1. Introduction expansion of the sine term and yielded with root finding methods a maximum error of 10−10 after inversion of a fifteen-degree Kepler’s equation relates the mean anomaly M and the eccentric polynomial. Another possibility to reduce the iteration is to use anomaly E in orbits with eccentricity e.
    [Show full text]
  • Experiment No
    1 LIST OF EXPERIMENTS 1. Study of logic gates. 2. Design and implementation of adders and subtractors using logic gates. 3. Design and implementation of code converters using logic gates. 4. Design and implementation of 4-bit binary adder/subtractor and BCD adder using IC 7483. 5. Design and implementation of 2-bit magnitude comparator using logic gates, 8- bit magnitude comparator using IC 7485. 6. Design and implementation of 16-bit odd/even parity checker/ generator using IC 74180. 7. Design and implementation of multiplexer and demultiplexer using logic gates and study of IC 74150 and IC 74154. 8. Design and implementation of encoder and decoder using logic gates and study of IC 7445 and IC 74147. 9. Construction and verification of 4-bit ripple counter and Mod-10/Mod-12 ripple counter. 10. Design and implementation of 3-bit synchronous up/down counter. 11. Implementation of SISO, SIPO, PISO and PIPO shift registers using flip-flops. KCTCET/2016-17/Odd/3rd/ETE/CSE/LM 2 EXPERIMENT NO. 01 STUDY OF LOGIC GATES AIM: To study about logic gates and verify their truth tables. APPARATUS REQUIRED: SL No. COMPONENT SPECIFICATION QTY 1. AND GATE IC 7408 1 2. OR GATE IC 7432 1 3. NOT GATE IC 7404 1 4. NAND GATE 2 I/P IC 7400 1 5. NOR GATE IC 7402 1 6. X-OR GATE IC 7486 1 7. NAND GATE 3 I/P IC 7410 1 8. IC TRAINER KIT - 1 9. PATCH CORD - 14 THEORY: Circuit that takes the logical decision and the process are called logic gates.
    [Show full text]
  • CORDIC V6.0 Logicore IP Product Guide
    CORDIC v6.0 LogiCORE IP Product Guide Vivado Design Suite PG105 August 6, 2021 Table of Contents IP Facts Chapter 1: Overview Navigating Content by Design Process . 5 Core Overview . 5 Feature Summary. 6 Applications . 6 Licensing and Ordering . 7 Chapter 2: Product Specification Performance. 8 Resource Utilization. 9 Port Descriptions . 9 Chapter 3: Designing with the Core Clocking. 12 Resets . 12 Protocol Description – AXI4-Stream . 12 Functional Description. 17 Input/Output Data Representation . 30 Chapter 4: Design Flow Steps Customizing and Generating the Core . 38 System Generator for DSP. 44 Constraining the Core . 44 Simulation . 45 Synthesis and Implementation . 46 Chapter 5: C Model Features . 47 Overview . 47 Installation . 48 C Model Interface. 49 CORDIC v6.0 Send Feedback 2 PG105 August 6, 2021 www.xilinx.com Compiling . 53 Linking. 53 Dependent Libraries . 54 Example . 55 Chapter 6: Test Bench Demonstration Test Bench . 56 Appendix A: Upgrading Migrating to the Vivado Design Suite. 58 Upgrading in the Vivado Design Suite . 58 Appendix B: Debugging Finding Help on Xilinx.com . 62 Debug Tools . 63 Simulation Debug. 64 AXI4-Stream Interface Debug . 65 Appendix C: Additional Resources and Legal Notices Xilinx Resources . 66 Documentation Navigator and Design Hubs . 66 References . 67 Revision History . 67 Please Read: Important Legal Notices . 68 CORDIC v6.0 Send Feedback 3 PG105 August 6, 2021 www.xilinx.com IP Facts Introduction LogiCORE IP Facts Table Core Specifics This Xilinx® LogiCORE™ IP core implements a Versal™ ACAP
    [Show full text]
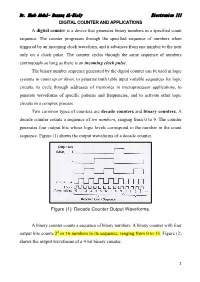
  • 1 DIGITAL COUNTER and APPLICATIONS a Digital Counter Is
    Dr. Ehab Abdul- Razzaq AL-Hialy Electronics III DIGITAL COUNTER AND APPLICATIONS A digital counter is a device that generates binary numbers in a specified count sequence. The counter progresses through the specified sequence of numbers when triggered by an incoming clock waveform, and it advances from one number to the next only on a clock pulse. The counter cycles through the same sequence of numbers continuously so long as there is an incoming clock pulse. The binary number sequence generated by the digital counter can be used in logic systems to count up or down, to generate truth table input variable sequences for logic circuits, to cycle through addresses of memories in microprocessor applications, to generate waveforms of specific patterns and frequencies, and to activate other logic circuits in a complex process. Two common types of counters are decade counters and binary counters. A decade counter counts a sequence of ten numbers, ranging from 0 to 9. The counter generates four output bits whose logic levels correspond to the number in the count sequence. Figure (1) shows the output waveforms of a decade counter. Figure (1): Decade Counter Output Waveforms. A binary counter counts a sequence of binary numbers. A binary counter with four output bits counts 24 or 16 numbers in its sequence, ranging from 0 to 15. Figure (2) shows-the output waveforms of a 4-bit binary counter. 1 Dr. Ehab Abdul- Razzaq AL-Hialy Electronics III Figure (2): Binary Counter Output Waveforms. EXAMPLE (1): Decade Counter. Problem: Determine the 4-bit decade counter output that corresponds to the waveforms shown in Figure (1).
    [Show full text]