VALUES of NON-ATOMIC VECTOR MEASURE GAMES Abraham
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

2Majors and Minors.Qxd.KA
APPLIED MATHEMATICS AND STATISTICS Spring 2007: updates since Fall 2006 are in red Applied Mathematics and Statistics (AMS) Major and Minor in Applied Mathematics and Statistics Department of Applied Mathematics and Statistics, College of Engineering and Applied Sciences CHAIRPERSON: James Glimm UNDERGRADUATE PROGRAM DIRECTOR: Alan C. Tucker UNDERGRADUATE SECRETARY: Elizabeth Ahmad OFFICE: P-139B Math Tower PHONE: (631) 632-8370 E-MAIL: [email protected] WEB ADDRESS: http://naples.cc.sunysb.edu/CEAS/amsweb.nsf Students majoring in Applied Mathematics and Statistics often double major in one of the following: Computer Science (CSE), Economics (ECO), Information Systems (ISE) Faculty Bradley Plohr, Adjunct Professor, Ph.D., he undergraduate program in Princeton University: Conservation laws; com- Hongshik Ahn, Associate Professor, Ph.D., Applied Mathematics and Statistics putational fluid dynamics. University of Wisconsin: Biostatistics; survival Taims to give mathematically ori- analysis. John Reinitz, Professor, Ph.D., Yale University: ented students a liberal education in quan- Mathematical biology. Esther Arkin, Professor, Ph.D., Stanford titative problem solving. The courses in University: Computational geometry; combina- Robert Rizzo, Assistant Professor, Ph.D., Yale this program survey a wide variety of torial optimization. University: Bioinformatics; drug design. mathematical theories and techniques Edward J. Beltrami, Professor Emeritus, Ph.D., David Sharp, Adjunct Professor, Ph.D., that are currently used by analysts and Adelphi University: Optimization; stochastic California Institute of Technology: Mathematical researchers in government, industry, and models. physics. science. Many of the applied mathematics Yung Ming Chen, Professor Emeritus, Ph.D., Ram P. Srivastav, Professor, D.Sc., University of courses give students the opportunity to New York University: Partial differential equa- Glasgow; Ph.D., University of Lucknow: Integral develop problem-solving techniques using equations; numerical solutions. -

Games of Threats
Accepted Manuscript Games of threats Elon Kohlberg, Abraham Neyman PII: S0899-8256(17)30190-2 DOI: https://doi.org/10.1016/j.geb.2017.10.018 Reference: YGAME 2771 To appear in: Games and Economic Behavior Received date: 30 August 2017 Please cite this article in press as: Kohlberg, E., Neyman, A. Games of threats. Games Econ. Behav. (2017), https://doi.org/10.1016/j.geb.2017.10.018 This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain. GAMES OF THREATS ELON KOHLBERG∗ AND ABRAHAM NEYMAN+ Abstract. Agameofthreatsonafinitesetofplayers,N, is a function d that assigns a real number to any coalition, S ⊆ N, such that d(S)=−d(N \S). A game of threats is not necessarily a coalitional game as it may fail to satisfy the condition d(∅)=0.We show that analogs of the classic Shapley axioms for coalitional games determine a unique value for games of threats. This value assigns to each player an average of d(S)acrossall the coalitions that include the player. Games of threats arise naturally in value theory for strategic games, and may have applications in other branches of game theory. 1. Introduction The Shapley value is the most widely studied solution concept of cooperative game theory. -

DEPARTMENT of ECONOMICS NEWSLETTER Issue #1
DEPARTMENT OF ECONOMICS NEWSLETTER Issue #1 DEPARTMENT OF ECONOMICS SEPTEMBER 2017 STONY BROOK UNIVERSITY IN THIS ISSUE Message from the Chair by Juan Carlos Conesa Greetings from the Department of Regarding news for the coming Economics in the College of Arts and academic year, we are very excited to Sciences at Stony Brook University! announce that David Wiczer, currently Since the beginning of the spring working for the Research Department of semester, we’ve celebrated several the Federal Reserve Bank of St Louis, 2017 Commencement Ceremony accomplishments of both students and will be joining us next semester as an Juan Carlos Conesa, Vincent J. Cassidy (BA ‘81), Anand George (BA ‘02) and Hugo faculty alike. I’d also like to tell you of Assistant Professor. David is an what’s to come for next year. enthusiastic researcher working on the Benitez‐Silva intersection of Macroeconomics and The beginning of 2017 has been a very Labor Economics, with a broad exciting time for our students. Six of our perspective combining theoretical, PhD students started looking for options computational and data analysis. We are to start exciting professional careers. really looking forward to David’s Arda Aktas specializes in Demographics, interaction with both students and and will be moving to a Post‐doctoral faculty alike. We are also happy to position at the World Population welcome Prof. Basak Horowitz, who will Program in the International Institute for join the Economics Department in Fall Applied Systems Analysis (IIASA), in 2017, as a new Lecturer. Basak’s Austria. Anju Bhandari specializes in research interests are microeconomic Macroeconomics, and has accepted a theory, economics of networks and New faculty, David Wiczer position as an Assistant Vice President matching theory, industrial organization with Citibank, NY. -

Games of Threats
Games of Threats The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters Citation Kohlberg, Elon, and Abraham Neyman. "Games of Threats." Games and Economic Behavior 108 (March 2018): 139–145. Citable link http://nrs.harvard.edu/urn-3:HUL.InstRepos:39148383 Terms of Use This article was downloaded from Harvard University’s DASH repository, and is made available under the terms and conditions applicable to Open Access Policy Articles, as set forth at http:// nrs.harvard.edu/urn-3:HUL.InstRepos:dash.current.terms-of- use#OAP GAMES OF THREATS ELON KOHLBERG∗ AND ABRAHAM NEYMAN+ Abstract. Agameofthreatsonafinitesetofplayers,N, is a function d that assigns a real number to any coalition, S ⊆ N, such that d(S)=−d(N \S). A game of threats is not necessarily a coalitional game as it may fail to satisfy the condition d(∅)=0.We show that analogs of the classic Shapley axioms for coalitional games determine a unique value for games of threats. This value assigns to each player an average of d(S)acrossall the coalitions that include the player. Games of threats arise naturally in value theory for strategic games, and may have applications in other branches of game theory. 1. Introduction The Shapley value is the most widely studied solution concept of cooperative game theory. It is defined on coalitional games, which are the standard objects of the theory. A coalitional game on a finite set of players, N, is a function v that assigns a real number to any subset (“coalition”), S ⊆ N, such that v(∅) = 0. -

2018 Unité De Recherche Dossier D'autoévaluation
Évaluation des unités de recherche Novembre 2016 Vague D Campagne d’évaluation 2017 – 2018 Unité de recherche Dossier d’autoévaluation Informations générales Nom de l’unité : Centre de Recherche en Mathématiques de la Décision Acronyme : CEREMADE UMR CNRS 7534 Champ de recherche de rattachement : Recherche Nom du directeur pour le contrat en cours : Vincent Rivoirard Nom du directeur pour le contrat à venir : Vincent Rivoirard Type de demande : Renouvellement à l’identique x Restructuration □ Création ex nihilo □ Établissements et organismes de rattachement : Liste des établissements et organismes tutelles de l’unité de recherche pour le contrat en cours et pour le prochain contrat (tutelles). Contrat en cours : | Prochain contrat : - Université Paris-Dauphine |- Université Paris-Dauphine - CNRS |- CNRS Choix de l’évaluation interdisciplinaire de l’unité de recherche ou de l’équipe interne : Oui □ Non x Vague D : campagne d’évaluation 2017 – 2018 1 Département d’évaluation de la recherche 2 Table des matières 1 Présentation du Ceremade7 1.1 Introduction..............................................7 1.2 Tableau des effectifs et moyens du Ceremade............................7 1.2.1 Effectifs............................................7 1.2.2 Parité.............................................9 1.2.3 Moyens financiers......................................9 1.2.4 Locaux occupés........................................ 10 1.2.5 Ressources documentaires.................................. 10 1.3 Politique scientifique......................................... 10 1.3.1 Missions et objectifs scientifiques.............................. 10 1.3.2 Structuration......................................... 11 1.3.3 Recrutements......................................... 12 1.3.4 Illustration de la mise en œuvre de la stratégie scientifique adoptée en 2012 en direction des applications........................................ 14 1.3.5 Programmes de soutien à la recherche du Ceremade déployés par la Fondation Dauphine, PSL, la FSMP et la Région Ile-de-France......................... -

2Majors and Minors.Qxd.KA
APPLIED MATHEMATICS AND STATISTICSSpring 2006: updates since Spring 2005 are in red Applied Mathematics and Statistics (AMS) Major and Minor in Applied Mathematics and Statistics Department of Applied Mathematics and Statistics, College of Engineering and Applied Sciences CHAIRPERSON: James Glimm UNDERGRADUATE PROGRAM DIRECTOR: Alan C. Tucker UNDERGRADUATE SECRETARY: Christine Rota OFFICE: P-139B Math Tower PHONE: (631) 632-8370 E-MAIL: [email protected] WEB ADDRESS: http://naples.cc.sunysb.edu/CEAS/amsweb.nsf Students majoring in Applied Mathematics and Statistics often double major in one of the following: Computer Science (CSE), Economics (ECO), Information Systems (ISE) Faculty Robert Rizzo, Assistant Professor, Ph.D., Yale he undergraduate program in University: Bioinformatics; drug design. Hongshik Ahn, Associate Professor, Ph.D., Applied Mathematics and Statistics University of Wisconsin: Biostatistics; survival David Sharp, Adjunct Professor, Ph.D., Taims to give mathematically ori- analysis. California Institute of Technology: Mathematical ented students a liberal education in quan- physics. Esther Arkin, Professor, Ph.D., Stanford titative problem solving. The courses in University: Computational geometry; combina- Ram P. Srivastav, Professor, D.Sc., University of this program survey a wide variety of torial optimization. Glasgow; Ph.D., University of Lucknow: Integral mathematical theories and techniques equations; numerical solutions. Edward J. Beltrami, Professor Emeritus, Ph.D., that are currently used by analysts and Adelphi University: Optimization; stochastic Michael Taksar, Professor Emeritus, Ph.D., researchers in government, industry, and models. Cornell University: Stochastic processes. science. Many of the applied mathematics Yung Ming Chen, Professor Emeritus, Ph.D., Reginald P. Tewarson, Professor Emeritus, courses give students the opportunity to New York University: Partial differential equa- Ph.D., Boston University: Numerical analysis; develop problem-solving techniques using biomathematics. -

A Formula for the Value of a Stochastic Game
A formula for the value of a stochastic game Luc Attiaa,1 and Miquel Oliu-Bartonb,1,2 aCentre de Mathematiques´ Appliquees,´ Ecole´ Polytechnique, 91128 Palaiseau, France; and bCentre de Recherches en Mathematiques´ de la Decision,´ Universite´ Paris-Dauphine, Paris Sciences et Lettres, 75016 Paris, France Edited by Robert J. Aumann, The Hebrew University, Jerusalem, Israel, and approved November 12, 2019 (received for review May 21, 2019) In 1953, Lloyd Shapley defined the model of stochastic games, a formula for the value (proved in Section 4). Section 5 describes which were the first general dynamic model of a game to be the algorithmic implications and tractability of these 2 formulas. defined, and proved that competitive stochastic games have a Section 6 concludes with remarks and extensions. discounted value. In 1982, Jean-Franc¸ois Mertens and Abraham Neyman proved that competitive stochastic games admit a robust 2. Context and Main Results solution concept, the value, which is equal to the limit of the To state our results precisely, we recall some definitions and well- discounted values as the discount rate goes to 0. Both contribu- known results about 2-player zero-sum games (Section 2A) and tions were published in PNAS. In the present paper, we provide a about finite competitive stochastic games (Section 2B). In Sec- tractable formula for the value of competitive stochastic games. tion 2C we give a brief overview of the relevant literature on finite competitive stochastic games. Our results are described in stochastic games j repeated games j dynamic programming Section 2D. Notation. Throughout this paper, N denotes the set of positive 1. -

Special Issue in Honor of Abraham Neyman
Int J Game Theory (2016) 45:3–9 DOI 10.1007/s00182-015-0518-2 PREFACE Special issue in honor of Abraham Neyman Olivier Gossner1 · Ori Haimanko2 · Eilon Solan3 Published online: 16 March 2016 © Springer-Verlag Berlin Heidelberg 2016 Preface The International Journal of Game Theory is proud to publish a special issue in honor of the contributions of Prof. Abraham Neyman to Game Theory. Abraham Neyman graduated from the Hebrew University of Jerusalem in 1977. His dissertaton, titled “Values of Games with a Continuum of Players”, was completed under the supervi- sion of Robert Aumann and was awarded the Aharon Katzir Prize for an Excellent Ph.D. thesis. After graduation he obtained a visiting position at Cornell University, from where he continued on to Berkeley. In 1982 Abraham Neyman joined the Hebrew University of Jerusalem, where he participated in the founding of the Center for the Study of Rationality in 1991. In 1985 he became one of the founders of the Center for Game Theory at Stony Brook University, where he worked for 16 years, in 1989 he was elected as a Fellow of the Econometric Society, and in 1999 he was selected a Charter Member of the Game Theory Society. Abraham Neyman was the advisor of 12 Ph.D. students. He has thus far published 67 articles and co-edited three books. He has also been the co-organizer of numer- ous conferences and workshops. He served as the Area Editor for Game Theory in B Eilon Solan [email protected] Olivier Gossner [email protected] Ori Haimanko [email protected] 1 École Polytechnique - CNRS, France, and London School of Economics, Paris, France, UK 2 Department of Economics, Ben-Gurion University of the Negev, Beer-Sheva 84105, Israel 3 School of Mathematical Sciences, Tel Aviv University, Tel Aviv 6997800, Israel 123 4 O. -

Cooperative Strategic Games
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Harvard University - DASH Cooperative Strategic Games The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters Citation Kohlberg, Elon, and Abraham Neyman. "Cooperative Strategic Games." Harvard Business School Working Paper, No. 17-075, February 2017. Citable link http://nrs.harvard.edu/urn-3:HUL.InstRepos:30838137 Terms of Use This article was downloaded from Harvard University’s DASH repository, and is made available under the terms and conditions applicable to Open Access Policy Articles, as set forth at http:// nrs.harvard.edu/urn-3:HUL.InstRepos:dash.current.terms-of- use#OAP Cooperative Strategic Games Elon Kohlberg Abraham Neyman Working Paper 17-075 Cooperative Strategic Games Elon Kohlberg Harvard Business School Abraham Neyman The Hebrew University of Jerusalem Working Paper 17-075 Copyright © 2017 by Elon Kohlberg and Abraham Neyman Working papers are in draft form. This working paper is distributed for purposes of comment and discussion only. It may not be reproduced without permission of the copyright holder. Copies of working papers are available from the author. Cooperative Strategic Games Elon Kohlberg∗ and Abraham Neymany February 5, 2017 Abstract We examine a solution concept, called the \value," for n-person strategic games. In applications, the value provides an a-priori assessment of the monetary worth of a player's position in a strategic game, comprising not only the player's contribution to the total payoff but also the player's ability to inflict losses on other players. -
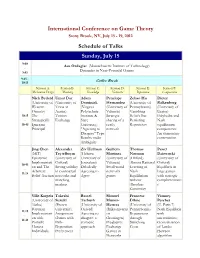
International Conference on Game Theory Schedule of Talks Sunday
International Conference on Game Theory Stony Brook, NY, July 15 - 19, 2012 Schedule of Talks Sunday, July 15 9:00 Asu Ozdaglar (Massachusetts Institute of Technology) - Dynamics in Near-Potential Games 9:45 9:45 - 10:15 Coffee Break Session A: Session B: Session C: Session D: Session E: Session F: Mechanism Design Matching Knowledge Networks Reputation Computation Nick Bedard Umut Dur Adam Penelope Zehao Hu Dieter (University of (University of Dominiak Hernandez (University of Balkenborg Western Texas at (Virginia (University of Pennsylvania) (University of Ontario) Austin) Polytechnic Valencia) Vanishing Exeter) 10:15 The Tuition Institute & Strategic Beliefs But Polyhedra and - Strategically Exchange State sharing of a Persisting Nash 10:45 Ignorant University) costly Reputation equilibrium Principal "Agreeing to network components: Disagree" Type An elementary Results under construction. Ambiguity Jing Chen Alexander Ziv Hellman Guillem Thomas Pawel (MIT) Teytelboym (Hebrew Martinez Norman Dziewuski Epistemic (University of University of (University of (Oxford) (University of Implementati Oxford) Jerusalem) Valencia) Almost-Rational Oxford) 10:45 on and The Strong stability Deludedly Small world Learning of Equilibria in - Arbitrary- in contractual Agreeing to networks Nash large games 11:15 Belief Auction networks and Agree games Equilibrium with strategic matching without complementarie markets Absolute s Continuity Ville Korpela Takeshi Bassel Manuel Francesc Vianney (University of Suzuki Tarbush Munoz- Dilme Perchet Turku) (Brown -

Curriculum Vitae Pradeep Dubey
Curriculum Vitae Pradeep Dubey Address Office: Center for Game Theory, Department of Economics SUNY at Stony Brook Stony Brook, NY 11794-4384 USA Phone: 631 632-7514 Fax: 631 632-7516 e-mail: [email protected] Field of Interest Game Theory and Mathematical Economics Degrees B.Sc. (Physics Honours), Delhi University, India, June 1971 Ph.D. (Applied Mathematics), Cornell University, Ithaca, NY, June, 1975 Scientific Societies Fellow of the Econometric Society Founding Member, Game Theory Society Economic Theory Fellow Academic Positions 1975-1978 Assistant Professor, School of Organization and Management (SOM) / Cowles Foundation for Research in Economics, Yale University. 1978-1984 Associate Professor, SOM and Cowles, Yale University. 1979-1980 Research Fellow (for the special year of game theory and mathematical economics), Institute for Advanced Studies, Hebrew University, Jerusalem (on leave from Yale University). 1982-1983 Senior Research Fellow, International Institute for Applied Systems Analysis, Austria (on leave, with a Senior Faculty Fellowship from Yale University). 1984-1985 Professor, Department of Economics, University of Illinois at Urbana-Champaign. 1985-1986 Professor, Department of Applied Mathematics and Statistics / Institute for Decision Sciences (IDS), SUNY Stony Brook. 1986-present: Leading Professor and Co-Director, Center for Game Theory in Economics, Department of Economics, SUNY Stony Brook. 2005-present: Visiting Professor, Cowles Foundation for Research in Economics, Yale University. Publications Dubey, Pradeep ; Sahi Siddhartha; Shubik, Martin. Money as Minimal Complexity , Games &Economic Behavior, 2018 Dubey, Pradeep ; Sahi Siddhartha; Shubik, Martin. Graphical Exchange Mechanisms, Games &Economic Behavior, 2018 Dubey, Pradeep ; Sahi, Siddhartha. Eliciting Performance: Deterministic versus Proportional Prizes, International Journal of Game Theory (Special issue in honor of Abraham Neyman). -

Game Theory Honoring Abraham Neyman's Scientific Achievements
Game Theory Honoring Abraham Neyman's Scientific Achievements: June 16-19, 2015 PROGRAM TUESDAY June 16, 2015 09:00 - 09:30 Welcome Session I Chair: Eilon Solan (Tel-Aviv University) 09:30 - 09:50 Eilon Solan (Tel-Aviv University) Stopping Games with Termination Rates 09:50 - 10:10 Fabien Gensbittel (Toulouse School of Economics) Zero-Sum Stopping Games with Asymmetric Information (joint with Christine Grün) 10:10 - 10:30 Miquel Oliu-Barton (Université Paris-Dauphine) The Asymptotic Value in Stochastic Games 10:30 - 10:50 Xiaoxi Li (University of Paris VI) Limit Value in Optimal Control with General Means (joint with Marc Quincampoix and Jérome Renault) 10:50 - 11:10 Break Session II Chair: Dov Samet (Tel-Aviv University) 11:10 - 11:30 Ehud Lehrer (Tel-Aviv University) No Folk Theorem in Repeated Games with Costly Monitoring 11:30 - 11:50 Antoine Salomon (Université Paris-Dauphine) Bayesian Repeated Games and Reputation 11:50 - 12:10 John Hillas (University of Auckland) Correlated Equilibria of Two Person Repeated Games with Random Signals (joint with Min Liu) 12:10 - 12:30 Gilad Bavly (Bar-Ilan University) How to Gamble Against All Odds 12:30 - 14:00 Lunch Session III Chair: John Hillas (University of Auckland) 14:00 - 14:20 Yoav Shoham (Stanford University) Intention, or, why the Formal Study of Rationality is Relevant to Software Engineering 14:20 - 14:40 Rene Levinsky (Max Planck Institute) Should I Remember More than You?: Best Response to Factor-Based Strategies 14:40 - 15:00 Dov Samet (Tel-Aviv University) Weak Dominance 15:00