Memory and C++
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Bit Nove Signal Interface Processor
www.audison.eu bit Nove Signal Interface Processor POWER SUPPLY CONNECTION Voltage 10.8 ÷ 15 VDC From / To Personal Computer 1 x Micro USB Operating power supply voltage 7.5 ÷ 14.4 VDC To Audison DRC AB / DRC MP 1 x AC Link Idling current 0.53 A Optical 2 sel Optical In 2 wire control +12 V enable Switched off without DRC 1 mA Mem D sel Memory D wire control GND enable Switched off with DRC 4.5 mA CROSSOVER Remote IN voltage 4 ÷ 15 VDC (1mA) Filter type Full / Hi pass / Low Pass / Band Pass Remote OUT voltage 10 ÷ 15 VDC (130 mA) Linkwitz @ 12/24 dB - Butterworth @ Filter mode and slope ART (Automatic Remote Turn ON) 2 ÷ 7 VDC 6/12/18/24 dB Crossover Frequency 68 steps @ 20 ÷ 20k Hz SIGNAL STAGE Phase control 0° / 180° Distortion - THD @ 1 kHz, 1 VRMS Output 0.005% EQUALIZER (20 ÷ 20K Hz) Bandwidth @ -3 dB 10 Hz ÷ 22 kHz S/N ratio @ A weighted Analog Input Equalizer Automatic De-Equalization N.9 Parametrics Equalizers: ±12 dB;10 pole; Master Input 102 dBA Output Equalizer 20 ÷ 20k Hz AUX Input 101.5 dBA OPTICAL IN1 / IN2 Inputs 110 dBA TIME ALIGNMENT Channel Separation @ 1 kHz 85 dBA Distance 0 ÷ 510 cm / 0 ÷ 200.8 inches Input sensitivity Pre Master 1.2 ÷ 8 VRMS Delay 0 ÷ 15 ms Input sensitivity Speaker Master 3 ÷ 20 VRMS Step 0,08 ms; 2,8 cm / 1.1 inch Input sensitivity AUX Master 0.3 ÷ 5 VRMS Fine SET 0,02 ms; 0,7 cm / 0.27 inch Input impedance Pre In / Speaker In / AUX 15 kΩ / 12 Ω / 15 kΩ GENERAL REQUIREMENTS Max Output Level (RMS) @ 0.1% THD 4 V PC connections USB 1.1 / 2.0 / 3.0 Compatible Microsoft Windows (32/64 bit): Vista, INPUT STAGE Software/PC requirements Windows 7, Windows 8, Windows 10 Low level (Pre) Ch1 ÷ Ch6; AUX L/R Video Resolution with screen resize min. -

The Hexadecimal Number System and Memory Addressing
C5537_App C_1107_03/16/2005 APPENDIX C The Hexadecimal Number System and Memory Addressing nderstanding the number system and the coding system that computers use to U store data and communicate with each other is fundamental to understanding how computers work. Early attempts to invent an electronic computing device met with disappointing results as long as inventors tried to use the decimal number sys- tem, with the digits 0–9. Then John Atanasoff proposed using a coding system that expressed everything in terms of different sequences of only two numerals: one repre- sented by the presence of a charge and one represented by the absence of a charge. The numbering system that can be supported by the expression of only two numerals is called base 2, or binary; it was invented by Ada Lovelace many years before, using the numerals 0 and 1. Under Atanasoff’s design, all numbers and other characters would be converted to this binary number system, and all storage, comparisons, and arithmetic would be done using it. Even today, this is one of the basic principles of computers. Every character or number entered into a computer is first converted into a series of 0s and 1s. Many coding schemes and techniques have been invented to manipulate these 0s and 1s, called bits for binary digits. The most widespread binary coding scheme for microcomputers, which is recog- nized as the microcomputer standard, is called ASCII (American Standard Code for Information Interchange). (Appendix B lists the binary code for the basic 127- character set.) In ASCII, each character is assigned an 8-bit code called a byte. -

Midterm-2020-Solution.Pdf
HONOR CODE Questions Sheet. A Lets C. [6 Points] 1. What type of address (heap,stack,static,code) does each value evaluate to Book1, Book1->name, Book1->author, &Book2? [4] 2. Will all of the print statements execute as expected? If NO, write print statement which will not execute as expected?[2] B. Mystery [8 Points] 3. When the above code executes, which line is modified? How many times? [2] 4. What is the value of register a6 at the end ? [2] 5. What is the value of register a4 at the end ? [2] 6. In one sentence what is this program calculating ? [2] C. C-to-RISC V Tree Search; Fill in the blanks below [12 points] D. RISCV - The MOD operation [8 points] 19. The data segment starts at address 0x10000000. What are the memory locations modified by this program and what are their values ? E Floating Point [8 points.] 20. What is the smallest nonzero positive value that can be represented? Write your answer as a numerical expression in the answer packet? [2] 21. Consider some positive normalized floating point number where p is represented as: What is the distance (i.e. the difference) between p and the next-largest number after p that can be represented? [2] 22. Now instead let p be a positive denormalized number described asp = 2y x 0.significand. What is the distance between p and the next largest number after p that can be represented? [2] 23. Sort the following minifloat numbers. [2] F. Numbers. [5] 24. What is the smallest number that this system can represent 6 digits (assume unsigned) ? [1] 25. -

2018-19 MAP 160 Byte File Layout Specifications
2018-19 MAP 160 Byte File Layout Specifications OVERVIEW: A) ISAC will provide an Eligibility Status File (ESF) record for each student to all schools listed as a college choice on the student’s Student Aid Report (SAR). The ESF records will be available daily as Record Type = 7. ESF records may be retrieved via the File Extraction option in MAP. B) Schools will transmit Payment Requests to ISAC via File Transfer Protocol (FTP) using the MAP 160byte layout and identify these with Record Type = 4. C) When payment requests are processed, ISAC will provide payment results to schools through the MAP system. The payment results records can be retrieved in the 160 byte format using the MAP Payment Results File Extraction Option. MAP results records have a Record Type = 5. The MAP Payment Results file contains some eligibility status data elements. Also, the same student record may appear on both the Payment Results and the Eligibility Status extract files. Schools may also use the Reports option in MAP to obtain payment results. D) To cancel Payment Requests, the school with the current Payment Results record on ISAC's Payment Database must transmit a matching record with MAP Payment Request Code = C, with the Requested Award Amount field equal to zero and the Enrollment Hours field equal to 0 along with other required data elements. These records must be transmitted to ISAC as Record Type = 4. E) Summary of Data Element Changes, revision (highlighted in grey) made to the 2018-19 layout. NONE 1 2018-19 MAP 160 Byte File Layout Specifications – 9/17 2018-19 MAP 160 Byte File Layout Specifications F) The following 160 byte record layout will be used for transmitting data between schools and ISAC. -

POINTER (IN C/C++) What Is a Pointer?
POINTER (IN C/C++) What is a pointer? Variable in a program is something with a name, the value of which can vary. The way the compiler and linker handles this is that it assigns a specific block of memory within the computer to hold the value of that variable. • The left side is the value in memory. • The right side is the address of that memory Dereferencing: • int bar = *foo_ptr; • *foo_ptr = 42; // set foo to 42 which is also effect bar = 42 • To dereference ted, go to memory address of 1776, the value contain in that is 25 which is what we need. Differences between & and * & is the reference operator and can be read as "address of“ * is the dereference operator and can be read as "value pointed by" A variable referenced with & can be dereferenced with *. • Andy = 25; • Ted = &andy; All expressions below are true: • andy == 25 // true • &andy == 1776 // true • ted == 1776 // true • *ted == 25 // true How to declare pointer? • Type + “*” + name of variable. • Example: int * number; • char * c; • • number or c is a variable is called a pointer variable How to use pointer? • int foo; • int *foo_ptr = &foo; • foo_ptr is declared as a pointer to int. We have initialized it to point to foo. • foo occupies some memory. Its location in memory is called its address. &foo is the address of foo Assignment and pointer: • int *foo_pr = 5; // wrong • int foo = 5; • int *foo_pr = &foo; // correct way Change the pointer to the next memory block: • int foo = 5; • int *foo_pr = &foo; • foo_pr ++; Pointer arithmetics • char *mychar; // sizeof 1 byte • short *myshort; // sizeof 2 bytes • long *mylong; // sizeof 4 byts • mychar++; // increase by 1 byte • myshort++; // increase by 2 bytes • mylong++; // increase by 4 bytes Increase pointer is different from increase the dereference • *P++; // unary operation: go to the address of the pointer then increase its address and return a value • (*P)++; // get the value from the address of p then increase the value by 1 Arrays: • int array[] = {45,46,47}; • we can call the first element in the array by saying: *array or array[0]. -

Signedness-Agnostic Program Analysis: Precise Integer Bounds for Low-Level Code
Signedness-Agnostic Program Analysis: Precise Integer Bounds for Low-Level Code Jorge A. Navas, Peter Schachte, Harald Søndergaard, and Peter J. Stuckey Department of Computing and Information Systems, The University of Melbourne, Victoria 3010, Australia Abstract. Many compilers target common back-ends, thereby avoid- ing the need to implement the same analyses for many different source languages. This has led to interest in static analysis of LLVM code. In LLVM (and similar languages) most signedness information associated with variables has been compiled away. Current analyses of LLVM code tend to assume that either all values are signed or all are unsigned (except where the code specifies the signedness). We show how program analysis can simultaneously consider each bit-string to be both signed and un- signed, thus improving precision, and we implement the idea for the spe- cific case of integer bounds analysis. Experimental evaluation shows that this provides higher precision at little extra cost. Our approach turns out to be beneficial even when all signedness information is available, such as when analysing C or Java code. 1 Introduction The “Low Level Virtual Machine” LLVM is rapidly gaining popularity as a target for compilers for a range of programming languages. As a result, the literature on static analysis of LLVM code is growing (for example, see [2, 7, 9, 11, 12]). LLVM IR (Intermediate Representation) carefully specifies the bit- width of all integer values, but in most cases does not specify whether values are signed or unsigned. This is because, for most operations, two’s complement arithmetic (treating the inputs as signed numbers) produces the same bit-vectors as unsigned arithmetic. -

Metaclasses: Generative C++
Metaclasses: Generative C++ Document Number: P0707 R3 Date: 2018-02-11 Reply-to: Herb Sutter ([email protected]) Audience: SG7, EWG Contents 1 Overview .............................................................................................................................................................2 2 Language: Metaclasses .......................................................................................................................................7 3 Library: Example metaclasses .......................................................................................................................... 18 4 Applying metaclasses: Qt moc and C++/WinRT .............................................................................................. 35 5 Alternatives for sourcedefinition transform syntax .................................................................................... 41 6 Alternatives for applying the transform .......................................................................................................... 43 7 FAQs ................................................................................................................................................................. 46 8 Revision history ............................................................................................................................................... 51 Major changes in R3: Switched to function-style declaration syntax per SG7 direction in Albuquerque (old: $class M new: constexpr void M(meta::type target, -

Bits and Bytes
BITS AND BYTES To understand how a computer works, you need to understand the BINARY SYSTEM. The binary system is a numbering system that uses only two digits—0 and 1. Although this may seem strange to humans, it fits the computer perfectly! A computer chip is made up of circuits. For each circuit, there are two possibilities: An electric current flows through the circuit (ON), or An electric current does not flow through the circuit (OFF) The number 1 represents an “on” circuit. The number 0 represents an “off” circuit. The two digits, 0 and 1, are called bits. The word bit comes from binary digit: Binary digit = bit Every time the computer “reads” an instruction, it translates that instruction into a series of bits (0’s and 1’s). In most computers every letter, number, and symbol is translated into eight bits, a combination of eight 0’s and 1’s. For example the letter A is translated into 01000001. The letter B is 01000010. Every single keystroke on the keyboard translates into a different combination of eight bits. A group of eight bits is called a byte. Therefore, a byte is a combination of eight 0’s and 1’s. Eight bits = 1 byte Capacity of computer memory, storage such as USB devices, DVD’s are measured in bytes. For example a Word file might be 35 KB while a picture taken by a digital camera might be 4.5 MG. Hard drives normally are measured in GB or TB: Kilobyte (KB) approximately 1,000 bytes MegaByte (MB) approximately 1,000,000 (million) bytes Gigabtye (GB) approximately 1,000,000,000 (billion) bytes Terabyte (TB) approximately 1,000,000,000,000 (trillion) bytes The binary code that computers use is called the ASCII (American Standard Code for Information Interchange) code. -

Meta-Class Features for Large-Scale Object Categorization on a Budget
Meta-Class Features for Large-Scale Object Categorization on a Budget Alessandro Bergamo Lorenzo Torresani Dartmouth College Hanover, NH, U.S.A. faleb, [email protected] Abstract cation accuracy over a predefined set of classes, and without consideration of the computational costs of the recognition. In this paper we introduce a novel image descriptor en- We believe that these two assumptions do not meet the abling accurate object categorization even with linear mod- requirements of modern applications of large-scale object els. Akin to the popular attribute descriptors, our feature categorization. For example, test-recognition efficiency is a vector comprises the outputs of a set of classifiers evaluated fundamental requirement to be able to scale object classi- on the image. However, unlike traditional attributes which fication to Web photo repositories, such as Flickr, which represent hand-selected object classes and predefined vi- are growing at rates of several millions new photos per sual properties, our features are learned automatically and day. Furthermore, while a fixed set of object classifiers can correspond to “abstract” categories, which we name meta- be used to annotate pictures with a set of predefined tags, classes. Each meta-class is a super-category obtained by the interactive nature of searching and browsing large im- grouping a set of object classes such that, collectively, they age collections calls for the ability to allow users to define are easy to distinguish from other sets of categories. By us- their own personal query categories to be recognized and ing “learnability” of the meta-classes as criterion for fea- retrieved from the database, ideally in real-time. -

IEEE Standard 754 for Binary Floating-Point Arithmetic
Work in Progress: Lecture Notes on the Status of IEEE 754 October 1, 1997 3:36 am Lecture Notes on the Status of IEEE Standard 754 for Binary Floating-Point Arithmetic Prof. W. Kahan Elect. Eng. & Computer Science University of California Berkeley CA 94720-1776 Introduction: Twenty years ago anarchy threatened floating-point arithmetic. Over a dozen commercially significant arithmetics boasted diverse wordsizes, precisions, rounding procedures and over/underflow behaviors, and more were in the works. “Portable” software intended to reconcile that numerical diversity had become unbearably costly to develop. Thirteen years ago, when IEEE 754 became official, major microprocessor manufacturers had already adopted it despite the challenge it posed to implementors. With unprecedented altruism, hardware designers had risen to its challenge in the belief that they would ease and encourage a vast burgeoning of numerical software. They did succeed to a considerable extent. Anyway, rounding anomalies that preoccupied all of us in the 1970s afflict only CRAY X-MPs — J90s now. Now atrophy threatens features of IEEE 754 caught in a vicious circle: Those features lack support in programming languages and compilers, so those features are mishandled and/or practically unusable, so those features are little known and less in demand, and so those features lack support in programming languages and compilers. To help break that circle, those features are discussed in these notes under the following headings: Representable Numbers, Normal and Subnormal, Infinite -

Numerical Computing with IEEE Floating Point Arithmetic This Page Intentionally Left Blank Numerical Computing with IEEE Floating Point Arithmetic
Numerical Computing with IEEE Floating Point Arithmetic This page intentionally left blank Numerical Computing with IEEE Floating Point Arithmetic Including One Theorem, One Rule of Thumb, and One Hundred and One Exercises Michael L. Overton Courant Institute of Mathematical Sciences New York University New York, New York siam. Society for Industrial and Applied Mathematics Philadelphia Copyright © 2001 by the Society for Industrial and Applied Mathematics. 1098765432 All rights reserved. Printed in the United States of America. No part of this book may be reproduced, stored, or transmitted in any manner without the written permission of the publisher. For information, write to the Society for Industrial and Applied Mathematics, 3600 University City Science Center, Philadelphia, PA 19104-2688. Library of Congress Cataloging-in-Publication Data Overton, Michael L Numerical computing with IEEE floating point arithmetic / Michael L Overton. p. cm. Includes bibliographical references and index. ISBN 0-89871-571-7 I. Computer arithmetic. 2. Floating-point arithmetic. 3. Numerical calculations. I. Title. QA76.9.M35O94200I O04'.0l'5l--dc2l 00-067941 SlcLJTL is a registered trademark. Dedicated to girls who like math especially my daughter Eleuthera Overton Sa This page intentionally left blank Contents Preface ix Acknowledgments xi 1 Introduction 1 2 The Real Numbers 5 3 Computer Representation of Numbers 9 4 IEEE Floating Point Representation 17 5 Rounding 25 6 Correctly Rounded Floating Point Operations 31 7 Exceptions 41 8 The Intel Microprocessors 49 9 Programming Languages 55 10 Floating Point in C 59 11 Cancellation 71 12 Conditioning of Problems 77 13 Stability of Algorithms 83 14 Conclusion 97 Bibliography 101 vii This page intentionally left blank Preface Numerical computing is a vital part of the modern scientific infrastructure. -
Bit, Byte, and Binary
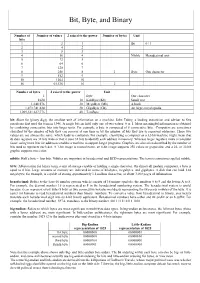
Bit, Byte, and Binary Number of Number of values 2 raised to the power Number of bytes Unit bits 1 2 1 Bit 0 / 1 2 4 2 3 8 3 4 16 4 Nibble Hexadecimal unit 5 32 5 6 64 6 7 128 7 8 256 8 1 Byte One character 9 512 9 10 1024 10 16 65,536 16 2 Number of bytes 2 raised to the power Unit 1 Byte One character 1024 10 KiloByte (Kb) Small text 1,048,576 20 MegaByte (Mb) A book 1,073,741,824 30 GigaByte (Gb) An large encyclopedia 1,099,511,627,776 40 TeraByte bit: Short for binary digit, the smallest unit of information on a machine. John Tukey, a leading statistician and adviser to five presidents first used the term in 1946. A single bit can hold only one of two values: 0 or 1. More meaningful information is obtained by combining consecutive bits into larger units. For example, a byte is composed of 8 consecutive bits. Computers are sometimes classified by the number of bits they can process at one time or by the number of bits they use to represent addresses. These two values are not always the same, which leads to confusion. For example, classifying a computer as a 32-bit machine might mean that its data registers are 32 bits wide or that it uses 32 bits to identify each address in memory. Whereas larger registers make a computer faster, using more bits for addresses enables a machine to support larger programs.