ANALYTICAL CHEMISTRY for TECHNOLOGISTS Part 1
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Transport of Dangerous Goods
ST/SG/AC.10/1/Rev.16 (Vol.I) Recommendations on the TRANSPORT OF DANGEROUS GOODS Model Regulations Volume I Sixteenth revised edition UNITED NATIONS New York and Geneva, 2009 NOTE The designations employed and the presentation of the material in this publication do not imply the expression of any opinion whatsoever on the part of the Secretariat of the United Nations concerning the legal status of any country, territory, city or area, or of its authorities, or concerning the delimitation of its frontiers or boundaries. ST/SG/AC.10/1/Rev.16 (Vol.I) Copyright © United Nations, 2009 All rights reserved. No part of this publication may, for sales purposes, be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, electrostatic, magnetic tape, mechanical, photocopying or otherwise, without prior permission in writing from the United Nations. UNITED NATIONS Sales No. E.09.VIII.2 ISBN 978-92-1-139136-7 (complete set of two volumes) ISSN 1014-5753 Volumes I and II not to be sold separately FOREWORD The Recommendations on the Transport of Dangerous Goods are addressed to governments and to the international organizations concerned with safety in the transport of dangerous goods. The first version, prepared by the United Nations Economic and Social Council's Committee of Experts on the Transport of Dangerous Goods, was published in 1956 (ST/ECA/43-E/CN.2/170). In response to developments in technology and the changing needs of users, they have been regularly amended and updated at succeeding sessions of the Committee of Experts pursuant to Resolution 645 G (XXIII) of 26 April 1957 of the Economic and Social Council and subsequent resolutions. -

1 Abietic Acid R Abrasive Silica for Polishing DR Acenaphthene M (LC
1 abietic acid R abrasive silica for polishing DR acenaphthene M (LC) acenaphthene quinone R acenaphthylene R acetal (see 1,1-diethoxyethane) acetaldehyde M (FC) acetaldehyde-d (CH3CDO) R acetaldehyde dimethyl acetal CH acetaldoxime R acetamide M (LC) acetamidinium chloride R acetamidoacrylic acid 2- NB acetamidobenzaldehyde p- R acetamidobenzenesulfonyl chloride 4- R acetamidodeoxythioglucopyranose triacetate 2- -2- -1- -β-D- 3,4,6- AB acetamidomethylthiazole 2- -4- PB acetanilide M (LC) acetazolamide R acetdimethylamide see dimethylacetamide, N,N- acethydrazide R acetic acid M (solv) acetic anhydride M (FC) acetmethylamide see methylacetamide, N- acetoacetamide R acetoacetanilide R acetoacetic acid, lithium salt R acetobromoglucose -α-D- NB acetohydroxamic acid R acetoin R acetol (hydroxyacetone) R acetonaphthalide (α)R acetone M (solv) acetone ,A.R. M (solv) acetone-d6 RM acetone cyanohydrin R acetonedicarboxylic acid ,dimethyl ester R acetonedicarboxylic acid -1,3- R acetone dimethyl acetal see dimethoxypropane 2,2- acetonitrile M (solv) acetonitrile-d3 RM acetonylacetone see hexanedione 2,5- acetonylbenzylhydroxycoumarin (3-(α- -4- R acetophenone M (LC) acetophenone oxime R acetophenone trimethylsilyl enol ether see phenyltrimethylsilyl... acetoxyacetone (oxopropyl acetate 2-) R acetoxybenzoic acid 4- DS acetoxynaphthoic acid 6- -2- R 2 acetylacetaldehyde dimethylacetal R acetylacetone (pentanedione -2,4-) M (C) acetylbenzonitrile p- R acetylbiphenyl 4- see phenylacetophenone, p- acetyl bromide M (FC) acetylbromothiophene 2- -5- -

STEM Issue 4 : Friday 26Th February 2021
STEM Issue 4 : Friday 26th February 2021 Bioprinting: Tissue Regeneration Structure of Computers J-58: The Heart of the Blackbird Dark Matter Welcome It has been over a year since we released our first issue of the Wilson’s Intrigue, the school STEM magazine written by students for the students. We would never have guessed a year ago that we would be facing a global pandemic. However, during these trying times, we should recognise the role of scientific innovation in our society as we seek to control the pandemic and try to adapt to the new normal. This issue, we have 23 excellent new articles for you to enjoy. We hope that, after reading them, you will agree with us when we say that issue 4 is our best issue yet. We also have lots of exciting things planned for the future. Issue 5 will have a new editorial team, led by Divy Dayal, and a number of new writers. Our Mission • Expand your knowledge • Contribute to the Wilson’s community • Make complicated parts of science more accessible • Popularise science and make it more interesting • Inspire creativity through wider research Acknowledgements Thank you to Mr Carew-Robinson, Mr Benn and Miss Roberts for their help in confirming the scientific accuracy of the articles. Thank you also to Mr Lissimore for helping publish this magazine and to Dr Whiting for letting us use S5 for our meetings. “Nothing in life is to be feared, it is only to be understood. Now is the time to understand more, so that we may fear less.” ― Marie Curie 2 The Wilson’s Intrigue Team Thank you to all these people who -

WO 2016/196440 Al 8 December 2016 (08.12.2016) P O P C T
(12) INTERNATIONAL APPLICATION PUBLISHED UNDER THE PATENT COOPERATION TREATY (PCT) (19) World Intellectual Property Organization International Bureau (10) International Publication Number (43) International Publication Date WO 2016/196440 Al 8 December 2016 (08.12.2016) P O P C T (51) International Patent Classification: (81) Designated States (unless otherwise indicated, for every A61P 3/04 (2006.01) A61K 33/40 (2006.01) kind of national protection available): AE, AG, AL, AM, A61P 9/10 (2006.01) A61K 38/44 (2006.01) AO, AT, AU, AZ, BA, BB, BG, BH, BN, BR, BW, BY, A61K 35/74 (2015.01) A61K 31/17 (2006.01) BZ, CA, CH, CL, CN, CO, CR, CU, CZ, DE, DK, DM, DO, DZ, EC, EE, EG, ES, FI, GB, GD, GE, GH, GM, GT, (21) International Application Number: HN, HR, HU, ID, IL, IN, IR, IS, JP, KE, KG, KN, KP, KR, PCT/US20 16/034973 KZ, LA, LC, LK, LR, LS, LU, LY, MA, MD, ME, MG, (22) International Filing Date: MK, MN, MW, MX, MY, MZ, NA, NG, NI, NO, NZ, OM, 3 1 May 2016 (3 1.05.2016) PA, PE, PG, PH, PL, PT, QA, RO, RS, RU, RW, SA, SC, SD, SE, SG, SK, SL, SM, ST, SV, SY, TH, TJ, TM, TN, (25) Filing Language: English TR, TT, TZ, UA, UG, US, UZ, VC, VN, ZA, ZM, ZW. (26) Publication Language: English (84) Designated States (unless otherwise indicated, for every (30) Priority Data: kind of regional protection available): ARIPO (BW, GH, 62/169,480 1 June 2015 (01 .06.2015) US GM, KE, LR, LS, MW, MZ, NA, RW, SD, SL, ST, SZ, 62/327,283 25 April 2016 (25.04.2016) US TZ, UG, ZM, ZW), Eurasian (AM, AZ, BY, KG, KZ, RU, TJ, TM), European (AL, AT, BE, BG, CH, CY, CZ, DE, (71) Applicant: XENO BIOSCIENCES INC. -

Chapter 2. Theoretical Background
Chapter 2 Chapter 2. Theoretical Background 2.1 Introduction Ferrites are the ferrimagnetic oxide which are semiconductors in nature, opened another entryway in material science. The necessity of ferrites with high resistivity led to synthesize different type of ferrites. The rising interest of low loss ferrites provoked in detail investigations on the different features of its conductivity and the effect of the different dopants on the structure, electrical and thermoelectric properties, hall mobility etc. The structural, magnetic and electrical properties of ferrites hinge on numerous factors such as preparation technique, synthesis parameters, site preference and cation distribution etc. [145-147]. In this chapter different theory, mathematical formulae for structural, dielectric, electrical and magnetic behaviors of ferrite and various synthesis procedures are briefly discussed. These theoretical models and formulae help in different ways for analysis, evaluation, conclusion and discussion of the outcomes obtained. Hence different theoretical models and synthesis techniques have been illustrated which endorse to understand the properties of ferrites. Page | 83 Theoretical background 2.2 Synthesis techniques A small amount of non-magnetic substitution can drastically change the properties of magnetic materials. So these are very conscious to its preparation procedure, processing parameters and impurity levels. In this manner the choice of synthesis technique for the ferrites and its composites is exceptionally critical. This guarantee to get profoundly pure single phasic materials. There are bunches of approach accessible for synthesizing ferrite materials. Here some preparation methods are briefly discussed. 2.2.1 Solid state reaction method The most versatile technique of synthesizing different metal oxides and other solid materials is solid state reaction technique or ceramic technique which include grinding of metal oxides, metal carbonates, metal oxalates or other compounds of relevant metals and heating the mixed powder at high temperature. -

Chemical Names and CAS Numbers Final
Chemical Abstract Chemical Formula Chemical Name Service (CAS) Number C3H8O 1‐propanol C4H7BrO2 2‐bromobutyric acid 80‐58‐0 GeH3COOH 2‐germaacetic acid C4H10 2‐methylpropane 75‐28‐5 C3H8O 2‐propanol 67‐63‐0 C6H10O3 4‐acetylbutyric acid 448671 C4H7BrO2 4‐bromobutyric acid 2623‐87‐2 CH3CHO acetaldehyde CH3CONH2 acetamide C8H9NO2 acetaminophen 103‐90‐2 − C2H3O2 acetate ion − CH3COO acetate ion C2H4O2 acetic acid 64‐19‐7 CH3COOH acetic acid (CH3)2CO acetone CH3COCl acetyl chloride C2H2 acetylene 74‐86‐2 HCCH acetylene C9H8O4 acetylsalicylic acid 50‐78‐2 H2C(CH)CN acrylonitrile C3H7NO2 Ala C3H7NO2 alanine 56‐41‐7 NaAlSi3O3 albite AlSb aluminium antimonide 25152‐52‐7 AlAs aluminium arsenide 22831‐42‐1 AlBO2 aluminium borate 61279‐70‐7 AlBO aluminium boron oxide 12041‐48‐4 AlBr3 aluminium bromide 7727‐15‐3 AlBr3•6H2O aluminium bromide hexahydrate 2149397 AlCl4Cs aluminium caesium tetrachloride 17992‐03‐9 AlCl3 aluminium chloride (anhydrous) 7446‐70‐0 AlCl3•6H2O aluminium chloride hexahydrate 7784‐13‐6 AlClO aluminium chloride oxide 13596‐11‐7 AlB2 aluminium diboride 12041‐50‐8 AlF2 aluminium difluoride 13569‐23‐8 AlF2O aluminium difluoride oxide 38344‐66‐0 AlB12 aluminium dodecaboride 12041‐54‐2 Al2F6 aluminium fluoride 17949‐86‐9 AlF3 aluminium fluoride 7784‐18‐1 Al(CHO2)3 aluminium formate 7360‐53‐4 1 of 75 Chemical Abstract Chemical Formula Chemical Name Service (CAS) Number Al(OH)3 aluminium hydroxide 21645‐51‐2 Al2I6 aluminium iodide 18898‐35‐6 AlI3 aluminium iodide 7784‐23‐8 AlBr aluminium monobromide 22359‐97‐3 AlCl aluminium monochloride -

2020 Emergency Response Guidebook
2020 A guidebook intended for use by first responders A guidebook intended for use by first responders during the initial phase of a transportation incident during the initial phase of a transportation incident involving hazardous materials/dangerous goods involving hazardous materials/dangerous goods EMERGENCY RESPONSE GUIDEBOOK THIS DOCUMENT SHOULD NOT BE USED TO DETERMINE COMPLIANCE WITH THE HAZARDOUS MATERIALS/ DANGEROUS GOODS REGULATIONS OR 2020 TO CREATE WORKER SAFETY DOCUMENTS EMERGENCY RESPONSE FOR SPECIFIC CHEMICALS GUIDEBOOK NOT FOR SALE This document is intended for distribution free of charge to Public Safety Organizations by the US Department of Transportation and Transport Canada. This copy may not be resold by commercial distributors. https://www.phmsa.dot.gov/hazmat https://www.tc.gc.ca/TDG http://www.sct.gob.mx SHIPPING PAPERS (DOCUMENTS) 24-HOUR EMERGENCY RESPONSE TELEPHONE NUMBERS For the purpose of this guidebook, shipping documents and shipping papers are synonymous. CANADA Shipping papers provide vital information regarding the hazardous materials/dangerous goods to 1. CANUTEC initiate protective actions. A consolidated version of the information found on shipping papers may 1-888-CANUTEC (226-8832) or 613-996-6666 * be found as follows: *666 (STAR 666) cellular (in Canada only) • Road – kept in the cab of a motor vehicle • Rail – kept in possession of a crew member UNITED STATES • Aviation – kept in possession of the pilot or aircraft employees • Marine – kept in a holder on the bridge of a vessel 1. CHEMTREC 1-800-424-9300 Information provided: (in the U.S., Canada and the U.S. Virgin Islands) • 4-digit identification number, UN or NA (go to yellow pages) For calls originating elsewhere: 703-527-3887 * • Proper shipping name (go to blue pages) • Hazard class or division number of material 2. -
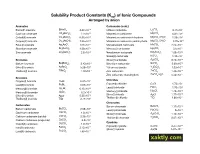
Solubility Product Constants (Ksp) of Ionic Compounds Arranged by Anion
Solubility Product Constants (Ksp) of Ionic Compounds Arranged by anion Arsenates Carbonates (cont.) -10 -4 Bismuth arsenate BiAsO4 4.43 10 Lithium carbonate Li2CO3 8.15 10 -33 -6 Cadmium arsenate Cd3(AsO4)2 2.2 10 Magnesium carbonate MgCO3 6.82 10 -29 -6 Cobalt(II) arsenate Co3(AsO4)2 6.80 10 Magnesium carbonate trihydrate MgCO3·3H2O 2.38 10 -36 -6 Copper(II) arsenate Cu3(AsO4)2 7.95 10 Magnesium carbonate pentahydrate MgCO3·5H2O 3.79 10 -22 -11 Silver(I) arsenate Ag3AsO4 1.03 10 Manganese(II) carbonate MnCO3 2.24 10 -19 -17 Strontium arsenate Sr3(AsO4)2 4.29 10 Mercury(I) carbonate Hg2CO3 3.6 10 -28 -33 Zinc arsenate Zn3(AsO4)2 2.8 10 Neodymium carbonate Nd2(CO3)3 1.08 10 -7 Nickel(II) carbonate NiCO3 1.42 10 -12 Bromates Silver(I) carbonate Ag2CO3 8.46 10 -4 -10 Barium bromate Ba(BrO3)2 2.43 10 Strontium carbonate SrCO3 5.60 10 -5 -31 Silver(I) bromate AgBrO3 5.38 10 Yttrium carbonate Y2(CO3)3 1.03 10 -4 -10 Thallium(I) bromate TlBrO3 1.10 10 Zinc carbonate ZnCO3 1.46 10 -11 Zinc carbonate monohydrate ZnCO3·H2O 5.42 10 Bromides -9 Chlorides Copper(I) bromide CuBr 6.27 10 -7 -6 Copper(I) chloride CuCl 1.72 10 Lead(II) bromide PbBr2 6.60 10 -5 -23 Lead(II) chloride PbCl2 1.70 10 Mercury(I) bromide Hg2Br2 6.40 10 -18 -20 Mercury(I) chloride Hg2Cl2 1.43 10 HgBr2 Mercury(II) bromide 6.2 10 -10 -13 Silver(I) chloride AgCl 1.77 10 Silver(I) bromide AgBr 5.35 10 -4 -6 Thallium(I) chloride TlCl 1.86 10 Thallium(I) bromide TlBr 3.71 10 Chromates Carbonates -10 Barium chromate BaCrO4 1.17 10 -9 Barium carbonate BaCO3 2.58 10 -13 Lead(II) chromate -

The Physico-Chemical Properties of Supramolecular Systems Involving Pharmaceuticals and Anions
THE PHYSICO-CHEMICAL PROPERTIES OF SUPRAMOLECULAR SYSTEMS INVOLVING PHARMACEUTICALS AND ANIONS By Maan Abdulrazzaq Suwiad Al-Nuaim A Thesis is Submitted for the Degree of Doctor of Philosophy Thermochemistry Laboratory Department of Chemistry Faculty of Engineering and Physical Sciences University of Surrey, United Kingdom January, 2016 © Maan Abdulrazzq Suwaid Al-Nuaim Abstract Abstract Currently, the discharge of pollutants to the environment is considered one of the biggest problems challenging chemists and environmental scientists. These pollutants come from different sources and might be carcinogenic, toxic or radioactive compounds which can cause serious health hazards to humans, animals and plants. Intensive thermodynamic studies by Danil de Namor and co-workers in the Thermochemistry Laboratory indicated that functionalisation of calix[4]pyrroles, cyclodextrines and calix[n]arenes ( n=4,6 ) leads to the production of selective macrocyclic receptors for the removal of anions, toxic heavy metals and other pollutants from water. The objective of this thesis is to design, synthesise and characterise macrocyclic receptors with suitable functional groups for the selective removal of drugs and anions from water. The drugs selected for this study are diclofenac, sodium diclofenac, clofibric acid, carbamazepine, aspirin and ibuprofen. This selection is based on the fact that these drugs are extensively used and as a result these contaminate sewage, surface and ground water. Supramolecular chemistry is one of the most important areas of chemistry which offers many advantages due to the efficient, fast and economical way for removing pollutants from water. In this thesis a large number of macrocycles based on calix[4]arene, calix[4]pyrrole resorc[4]arene and pyrogalol[4]arene have been synthesised and characterised by 1H NMR and microanalysis. -

Nomenclature of Inorganic Chemistry (IUPAC Recommendations 2005)
NOMENCLATURE OF INORGANIC CHEMISTRY IUPAC Recommendations 2005 IUPAC Periodic Table of the Elements 118 1 2 21314151617 H He 3 4 5 6 7 8 9 10 Li Be B C N O F Ne 11 12 13 14 15 16 17 18 3456 78910 11 12 Na Mg Al Si P S Cl Ar 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 K Ca Sc Ti V Cr Mn Fe Co Ni Cu Zn Ga Ge As Se Br Kr 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 Rb Sr Y Zr Nb Mo Tc Ru Rh Pd Ag Cd In Sn Sb Te I Xe 55 56 * 57− 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 Cs Ba lanthanoids Hf Ta W Re Os Ir Pt Au Hg Tl Pb Bi Po At Rn 87 88 ‡ 89− 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 Fr Ra actinoids Rf Db Sg Bh Hs Mt Ds Rg Uub Uut Uuq Uup Uuh Uus Uuo * 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 La Ce Pr Nd Pm Sm Eu Gd Tb Dy Ho Er Tm Yb Lu ‡ 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 Ac Th Pa U Np Pu Am Cm Bk Cf Es Fm Md No Lr International Union of Pure and Applied Chemistry Nomenclature of Inorganic Chemistry IUPAC RECOMMENDATIONS 2005 Issued by the Division of Chemical Nomenclature and Structure Representation in collaboration with the Division of Inorganic Chemistry Prepared for publication by Neil G. -

Chemistry-Iv
B.Ed. Science Education CHEMISTRY-IV UNIT 1-9 Course Code: 6459 Science Education Department Faculty of Education ALLAMA IQBAL OPEN UNIVERSITY ISLAMABAD i (All rights reserved with the publisher) 1st Printing ..................................................................................................... 2020 Number of Copies ................................................................................................ 1000 Course Coordinator ................................................................................ Dr. Aftab Ahmed Printer .............................................Allama Iqbal Open University, Islamabad Publisher .............................................Allama Iqbal Open University, Islamabad ii COURSE TEAM Dean Prof. Dr. Nasir Mehmood Chairman Prof. Dr. Nasir Mahmood Course Development Coordinator Dr. Aftab Ahmed Writers: 1. Dr. Aftab Ahmed Lecturer, Department of Science Education, AIOU. 2. Ms. Raheela Department of Chemistry, University of Wah, Wah Cantt. 3. Ms. Fareeha Department of Chemistry, University of Wah, Wah Cantt. 4. Mr. Zia ul Haq Zia Lecturer, Federal College of Education, Islamabad. 5. Syeda Koukab Lecturer, Federal College of Education, Islamabad. 6. Ms. Sadia Khatoon M.Phil. Scholar, Department of Science Education, AIOU. Reviewers: 1. Dr. Muhammad Zaigham Qadeer Associate Professor, Department of Chemistry, AIOU 2. Dr. Aftab Ahmed Lecturer, Department of Science Education, AIOU. 3. Mr. Arshad Mehmood Qamar Lecturer, Department of Science Education, AIOU. 4. Mr. Zia ul Haq Zia Lecturer, -

TAC-Hazgoods
Tariff Advisory Committee Sheet No.1 CATEGORY I Accoroides Gums Acrylic sheets Accumulator Acid Activated carbon Acenaphthene Activated Manganese Acetate Silk Agarbatti (Dhoop) Acetoacetanilide Agerite powder Acetylene black Acid (not otherwise specifically provided) Acrylamide Acrylic acid Aldrin (insecticide) Acrylic powder Algae Tariff Advisory Committee Sheet No.2 All flammable liquids having Animal oil flash point above 65oC. Animal protein Almond oil Animal skin Aloe resin Anime (a resin) Aluminium Chloride Anthracene Aluminium paste Antimony Pentafluoride Aluminium resinate Antimony Pentasulfide Amber Antimony sulphate Ammonium Bromide Antimony sulphide Ammonium Chloride Antimony trisulphate Ammonium Fluoride Antimony trisulphide Ammonium Sulphate Arachis oil Amonia-acqueous soln. or spirits Arecanuts of ammonia exceeding 30% Arsenic Chloride concentration Arsenic pentasulphide Anethole Arsenic sulphide Animal black Arsenic Trisulfide Animal glue Artificial edible fat Tariff Advisory Committee Sheet No.3 Artificial horn Beet tallow (Aldrin) Artificial leather Benzoin (resin) Artificial Silk Benzoin (resinoid) Artificial wool Betal Nuts Asafoetida (gum resin) Birch (bark) oil Asafoetida oil Bisphenol Asphalt /Asphalt sheet Bitumen/Bituminised Asphalted paper craftpaper/felt Balata , Balsam of Peru Blacks of all kinds (not otherwise Bamboo mats Speciafically provided for) Barium Carbonate Borneo Camphor Barium Sulphide Borneol Barley Borneo tallow Baryllium Dustor powder Bornyl acetate Bed feathers (Down) Boron trichloride Beedi leaves