DOCSLIB.ORG

Arithmetic Circuits & Multipliers

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Arithmetic Circuits & Multipliers Arithmetic Circuits & Multipliers • Addition, subtraction • Performance issues -- ripple carry -- carry bypass -- carry skip -- carry lookahead • Multipliers Reminder: Lab #3 due tonight! Pizza Wed 6p 6.111 Fall 2017 Lecture 8 1 Signed integers: 2’s complement N bits -2N-1 2N-2 … … … 23 22 21 20 Range: – 2N-1 to 2N-1 –1 “sign bit” “decimal” point 8-bit 2’s complement example: 11010110 = –27 + 26 + 24 + 22 + 21 = – 128 + 64 + 16 + 4 + 2 = – 42 If we use a two’s complement representation for signed integers, the same binary addition mod 2n procedure will work for adding positive and negative numbers (don’t need separate subtraction rules). The same procedure will also handle unsigned numbers! By moving the implicit location of “decimal” point, we can represent fractions too: 1101.0110 = –23 + 22 + 20 + 2-2 + 2-3 = – 8 + 4 + 1 + 0.25 + 0.125 = – 2.625 6.111 Fall 2017 Lecture 8 2 Sign extension Consider the 8-bit 2’s complement representation of: 42 = 00101010 -5 = ~00000101 + 1 = 11111010 + 1 = 11111011 What is their 16-bit 2’s complement representation? 4242 == 00000000________00101010000000000010101000101010 -5-5 == ________11111011________111110111111111111111011 Extend the MSB (aka the “sign bit”) into the higher-order bit positions 6.111 Fall 2017 Lecture 8 3 Adder: a circuit that does addition Here’s an example of binary addition as one might do it by “hand”: Carries from previous 1 1 0 1 column Adding two N-bit 1101 numbers produces an + 0101 (N+1)-bit result 10010 If we build a circuit that implements one column: we can quickly build a circuit to add two 4-bit numbers… “Ripple- carry adder” 6.111 Fall 2017 Lecture 8 4 “Full Adder” building block ABCSCO 00000 00110 01010 The “half adder” circuit has only the 01101 A and B inputs 10010 10101 11001 11111 S A B C CO ABC ABC ABC ABC (A A)BC (B B)AC AB(C C) BC AC AB 6.111 Fall 2017 Lecture 8 5 Subtraction: A-B = A + (-B) Using 2’s complement representation: –B = ~B + 1 ~ = bit-wise complement So let’s build an arithmetic unit that does both addition and subtraction. Operation selected by control input: But what about the “+1”? 6.111 Fall 2017 Lecture 8 6 Condition Codes Besides the sum, one often wants four other bits of information from an arithmetic unit: To compare A and B, perform A–B and use Z (zero): result is = 0 big NOR gate condition codes: Signed comparison: N (negative): result is < 0 S N-1 LT NV C (carry): indicates an add in the most LE Z+(N V) significant position produced a carry, e.g., EQ Z 1111 + 0001 from last FA NE ~Z GE ~(NV) V (overflow): indicates that the answer GT ~(Z+(NV)) has too many bits to be represented correctly by the result width, e.g., Unsigned comparison: 0111 + 0111 LTU C LEU C+Z V A B S A B S GEU ~C N1 N1 N1 N1 N1 N1 GTU ~(C+Z) V COUT CIN N1 N1 6.111 Fall 2017 Lecture 8 7 Condition Codes in Verilog Z (zero): result is = 0 N (negative): result is < 0 C (carry): indicates an add wire signed [31:0] a,b,s; in the most significant wire z,n,v,c; assign {c,s} = a + b; position produced a carry, assign z = ~|s; e.g., 1111 + 0001 assign n = s[31]; assign v = a[31]^b[31]^s[31]^c; V (overflow): indicates that the answer has too many Might be better to use sum-of- bits to be represented products formula for V from previous correctly by the result slide if using LUT implementation width, e.g., 0111 + 0111 (only 3 variables instead of 4). 6.111 Fall 2017 Lecture 8 8 Modular Arithmetic The Verilog arithmetic operators (+,-,*) all produce full-precision results, e.g., adding two 8-bit numbers produces a 9-bit result. In many designs one chooses a “word size” (many computers use 32 or 64 bits) and all arithmetic results are truncated to that number of bits, i.e., arithmetic is performed modulo 2word size. Using a fixed word size can lead to overflow, e.g., when the operation produces a result that’s too large to fit in the word size. One can •Avoid overflow: choose a sufficiently large word size •Detect overflow: have the hardware remember if an operation produced an overflow – trap or check status at end •Embrace overflow: sometimes this is exactly what you want, e.g., when doing index arithmetic for circular buffers of size 2N. •“Correct” overflow: replace result with most positive or most negative number as appropriate, aka saturating arithmetic. Good for digital signal processing. 6.111 Fall 2017 Lecture 8 9 Speed: tPD of Ripple-carry Adder CO = AB + ACI + BCI Worst-case path: carry propagation from LSB to MSB, (N) is read e.g., when adding 11…111 to 00…001. “order N” : means that the latency of our tPD = (N-1)*(tPD,OR + tPD,AND) + tPD,XOR (N) adder grows at worst in proportion to CI to CO CIN-1 to SN-1 the number of bits in the operands. 6.111 Fall 2017 Lecture 8 10 How about the tPD of this circuit? Cn-1 Cn-2 C2 C1 C0 Is the tPD of this circuit = 2 * tPD,N-BIT RIPPLE ? Nope! tPD of this circuit = tPD,N-BIT RIPPLE + tPD,FA !!! Timing analysis is tricky! 6.111 Fall 2017 Lecture 8 11 Alternate Adder Logic Formulation How to Speed up the Critical (Carry) Path? (How to Build a Fast Adder?) A B Full Cin C Adder o S Generate (G) = AB Propagate (P) = A B Note: can also use P = A + B for Co Faster carry logic Let’s see if we can improve the speed by rewriting the equations for COUT: C = AB + AC + BC AB OUT IN IN = AB + (A + B)CIN where G = AB COUT CIN = G + P CIN P = A + B generate propagate S Actually, P is usually module fa(input a,b,cin, output s,cout); wire g = a & b; defined as P = A^B wire p = a ^ b; which won’t change assign s = p ^ cin; COUT but will allow us assign cout = g | (p & cin); to express S as a endmodule simple function : S = P^CIN 6.111 Fall 2017 Lecture 8 13 Virtex II Adder Implementation Cout LUT: AB B A Y = A B Cin P G Dedicated adder logic 1 half-Slice = 1-bit adder Cin 6.111 Fall 2017 Lecture 8 14 Virtex II Carry Chain 1 CLB = 4 Slices = 2, 4-bit adders 64-bit Adder: 16 CLBs A[63:0] + Y[63:0] B[63:0] Y[64] A[63:60] CLB15 B[63:60] Y[63:60] A[7:4] CLB1 B[7:4] Y[7:4] A[3:0] CLB0 B[3:0] Y[3:0] CLBs must be in same column 6.111 Fall 2017 Lecture 8 15 Carry Bypass Adder A0 B0 A1 B1 A2 B2 A3 B3 P,G P,G P,G P,G Can compute P, G P0 G0 P1 G1 P2 G2 P3 G3 in parallel for all bits C/S C/S C/S Ci,0 C/S Co,0 Co,1 Co,2 Co,3 BP= P0P1P2P3 P,G P,G P,G P,G P0 G0 P1 G1 P2 G2 P3 G3 Ci,0 0 C/S C/S C/S C/S Co,3 Co,0 Co,1 Co,2 1 Key Idea: if (P0 P1 P2 P3) then Co,3 = Ci,0 6.111 Fall 2017 Lecture 8 16 16-bit Carry Bypass Adder BP= P0P1P2P3 BP= P4P5P6P7 BP= P8P9P10P11 BP= P12P13P14P15 P,G P,G P,G P,G P,G P,G P,G P,G P,G P,G P,G P,G P,G P,G P,G P,G Ci,0 Co,3 C C C/S C/S C/S C/S 0 o,7 o,11 C/S C/S C/S C/S 0 C/S C/S C/S C/S 0 C/S C/S C/S C/S 0 Co,0 Co,1 C C C o,2 1 o,4 o,5 Co,6 C C C C C C 1 o,8 o,9 o,10 1 o,12 o,13 o,14 1 Co,15 What is the worst case propagation delay for the 16-bit adder? Assume the following for delay each gate: P, G from A, B: 1 delay unit P, G, Ci to Co or Sum for a C/S: 1 delay unit 2:1 mux delay: 1 delay unit 6.111 Fall 2017 Lecture 8 17 Critical Path Analysis BP= P P P P 0 1 2 3 BP2= P4P5P6P7 BP3= P8P9P10P11 BP4= P12P13P14P15 P,G P,G P,G P,G P,G P,G P,G P,G P,G P,G P,G P,G P,G P,G P,G P,G Ci,0 Co,3 C C C/S C/S C/S C/S 0 o,7 o,11 C/S C/S C/S C/S 0 C/S C/S C/S C/S 0 C/S C/S C/S C/S 0 Co,0 Co,1 C C C o,2 1 o,4 o,5 Co,6 C C C C C C 1 o,8 o,9 o,10 1 o,12 o,13 o,14 1 Co,15 For the second stage, is the critical path: BP2 = 0 or BP2 = 1 ? Message: Timing analysis is very tricky – Must carefully consider data dependencies for false paths 6.111 Fall 2017 Lecture 8 18 Carry Bypass vs Ripple Carry Ripple Carry: tadder = (N-1) tcarry + tsum Carry Bypass: tadder = 2(M-1) tcarry + tsum + (N/M-1) tbypass This image cannot currently Thisbe imagedisplayed.
Load more

Recommended publications
  • Lesson 2: the Multiplication of Polynomials
    NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 2 M1 ALGEBRA II Lesson 2: The Multiplication of Polynomials Student Outcomes . Students develop the distributive property for application to polynomial multiplication. Students connect multiplication of polynomials with multiplication of multi-digit integers. Lesson Notes This lesson begins to address standards A-SSE.A.2 and A-APR.C.4 directly and provides opportunities for students to practice MP.7 and MP.8. The work is scaffolded to allow students to discern patterns in repeated calculations, leading to some general polynomial identities that are explored further in the remaining lessons of this module. As in the last lesson, if students struggle with this lesson, they may need to review concepts covered in previous grades, such as: The connection between area properties and the distributive property: Grade 7, Module 6, Lesson 21. Introduction to the table method of multiplying polynomials: Algebra I, Module 1, Lesson 9. Multiplying polynomials (in the context of quadratics): Algebra I, Module 4, Lessons 1 and 2. Since division is the inverse operation of multiplication, it is important to make sure that your students understand how to multiply polynomials before moving on to division of polynomials in Lesson 3 of this module. In Lesson 3, division is explored using the reverse tabular method, so it is important for students to work through the table diagrams in this lesson to prepare them for the upcoming work. There continues to be a sharp distinction in this curriculum between justification and proof, such as justifying the identity (푎 + 푏)2 = 푎2 + 2푎푏 + 푏 using area properties and proving the identity using the distributive property.
    [Show full text]
  • Chapter 2. Multiplication and Division of Whole Numbers in the Last Chapter You Saw That Addition and Subtraction Were Inverse Mathematical Operations
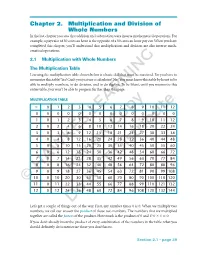
    Chapter 2. Multiplication and Division of Whole Numbers In the last chapter you saw that addition and subtraction were inverse mathematical operations. For example, a pay raise of 50 cents an hour is the opposite of a 50 cents an hour pay cut. When you have completed this chapter, you’ll understand that multiplication and division are also inverse math- ematical operations. 2.1 Multiplication with Whole Numbers The Multiplication Table Learning the multiplication table shown below is a basic skill that must be mastered. Do you have to memorize this table? Yes! Can’t you just use a calculator? No! You must know this table by heart to be able to multiply numbers, to do division, and to do algebra. To be blunt, until you memorize this entire table, you won’t be able to progress further than this page. MULTIPLICATION TABLE ϫ 012 345 67 89101112 0 000 000LEARNING 00 000 00 1 012 345 67 89101112 2 024 681012Copy14 16 18 20 22 24 3 036 9121518212427303336 4 0481216 20 24 28 32 36 40 44 48 5051015202530354045505560 6061218243036424854606672Distribute 7071421283542495663707784 8081624324048566472808896 90918273HAWKESReview645546372819099108 10 0 10 20 30 40 50 60 70 80 90 100 110 120 ©11 0 11 22 33 44NOT 55 66 77 88 99 110 121 132 12 0 12 24 36 48 60 72 84 96 108 120 132 144 Do Let’s get a couple of things out of the way. First, any number times 0 is 0. When we multiply two numbers, we call our answer the product of those two numbers.
    [Show full text]
  • Grade 7/8 Math Circles the Scale of Numbers Introduction
    Faculty of Mathematics Centre for Education in Waterloo, Ontario N2L 3G1 Mathematics and Computing Grade 7/8 Math Circles November 21/22/23, 2017 The Scale of Numbers Introduction Last week we quickly took a look at scientific notation, which is one way we can write down really big numbers. We can also use scientific notation to write very small numbers. 1 × 103 = 1; 000 1 × 102 = 100 1 × 101 = 10 1 × 100 = 1 1 × 10−1 = 0:1 1 × 10−2 = 0:01 1 × 10−3 = 0:001 As you can see above, every time the value of the exponent decreases, the number gets smaller by a factor of 10. This pattern continues even into negative exponent values! Another way of picturing negative exponents is as a division by a positive exponent. 1 10−6 = = 0:000001 106 In this lesson we will be looking at some famous, interesting, or important small numbers, and begin slowly working our way up to the biggest numbers ever used in mathematics! Obviously we can come up with any arbitrary number that is either extremely small or extremely large, but the purpose of this lesson is to only look at numbers with some kind of mathematical or scientific significance. 1 Extremely Small Numbers 1. Zero • Zero or `0' is the number that represents nothingness. It is the number with the smallest magnitude. • Zero only began being used as a number around the year 500. Before this, ancient mathematicians struggled with the concept of `nothing' being `something'. 2. Planck's Constant This is the smallest number that we will be looking at today other than zero.
    [Show full text]
  • Vax 6135 Car Vax Uk - Service Parts List
    VAX 6135 CAR VAX UK - SERVICE PARTS LIST Item Vax Part No. Description Price Code Service Item Item Vax Part No. Description Price Code Service Item 2 1-2-31-01-006 FILTER-FOAM-EXHAUST S1 CS 34 1-2-30-01-015 SEAL-FILTER/RESERVOIR K1 S 5 1-2-11-04-007 CABLE CLAMP L1 CS 35 1-3-15-03-007 FILTER HSG ASSY-UNIV-BLACK T3 S 29 1-2-31-01-002 FILTER DISC-BONDINI A1 CS 39 1-2-14-02-001 BALL VALVE N1 S 32 1-2-31-01-007 FILTER -FIBRE-MOULDED X1 CS 40 1-3-09-06-007 RESERVOIR ASSY-UNIV-BLACK W3 S 44 1-3-13-02-001 UPHOLSTERY TOOL Y1 CS 41 1-2-30-02-002 SEAL-CONICAL DUCT D2 S 47 1-2-39-01-010 CREVICE TOOL Y1 CS 42 1-2-30-02-003 SEAL-EXHAUST D2 S 48 1-3-13-01-001 DUSTBRUSH H2 CS 43 1-2-124731-12 RECOVERY BUCKET/SPIDER ASSY Z3 S 50 1-2-13-02-002 TUBE-EXTN-STAINLESS B3 CS 45 1-2-32-01-002 CASTOR-TWO WHEEL X1 S 52 1-3-18-01-022 HOSE & GRIP ASSY W3 CS 60 1-9-124423-00 TUBE-PUMP TO QRV A1 S 53 1-9-124962-00 WASH HEAD J3 CS 62 1-1-06-01-073 FEMALE QRV ASSY S2 S 54 1-9-124961-00 FLOOR BRUSH F3 CS 63 1-3-124422-00 ELBOW-QRV-ET408 C2 S 64 1-2-11-03-007 RETAINER CLIP-SPRING H1 CS 65 1-2-13-04-008 INLET TUBE-PVC A1 S 74 1-2-124594-00 UPHOLSTERY WASH TOOL K3 CS 66 1-3-124424-00 FIXING STRAP-ET408 L1 S 75 1-9-125226-00 TURBO TOOL-100mm R3 CS 67 1-7-124677-00 FILTER-WATER-INLET E2 S 77 1-9-125549-00 CREVICE TOOL-EXTRA LONG G2 CS 68 1-5-124419-00 PUMP-ET408 S3 S 101 1-2-124805-00 WATER TUBE ASSY-STRAIGHT Z2 CS 69 1-6-124425-00 SEAL-PUMP ET408 L1 S 3 1-3-124588-03 COVER-ACCESS-B R GREEN X1 NS 99 1-2-07-03-001 DUCT-CONICAL X1 S 6 1-2-36-04-004 CORD PROTECTOR A1 NS 102
    [Show full text]
  • CS 6290 Chapter 1
    Spring 2011 Prof. Hyesoon Kim Xbox 360 System Architecture, „Anderews, Baker • 3 CPU cores – 4-way SIMD vector units – 8-way 1MB L2 cache (3.2 GHz) – 2 way SMT • 48 unified shaders • 3D graphics units • 512-Mbyte DRAM main memory • FSB (Front-side bus): 5.4 Gbps/pin/s (16 pins) • 10.8 Gbyte/s read and write • Xbox 360: Big endian • Windows: Little endian http://msdn.microsoft.com/en-us/library/cc308005(VS.85).aspx • L2 cache : – Greedy allocation algorithm – Different workloads have different working set sizes • 2-way 32 Kbyte L1 I-cache • 4-way 32 Kbyte L1 data cache • Write through, no write allocation • Cache block size :128B (high spatial locality) • 2-way SMT, • 2 insts/cycle, • In-order issue • Separate vector/scalar issue queue (VIQ) Vector Vector Execution Unit Instructions Scalar Scalar Execution Unit • First game console by Microsoft, released in 2001, $299 Glorified PC – 733 Mhz x86 Intel CPU, 64MB DRAM, NVIDIA GPU (graphics) – Ran modified version of Windows OS – ~25 million sold • XBox 360 – Second generation, released in 2005, $299-$399 – All-new custom hardware – 3.2 Ghz PowerPC IBM processor (custom design for XBox 360) – ATI graphics chip (custom design for XBox 360) – 34+ million sold (as of 2009) • Design principles of XBox 360 [Andrews & Baker] - Value for 5-7 years -!ig performance increase over last generation - Support anti-aliased high-definition video (720*1280*4 @ 30+ fps) - extremely high pixel fill rate (goal: 100+ million pixels/s) - Flexible to suit dynamic range of games - balance hardware, homogenous resources - Programmability (easy to program) Slide is from http://www.cis.upenn.edu/~cis501/lectures/12_xbox.pdf • Code name of Xbox 360‟s core • Shared cell (playstation processor) ‟s design philosophy.
    [Show full text]
  • The Notion Of" Unimaginable Numbers" in Computational Number Theory
    Beyond Knuth’s notation for “Unimaginable Numbers” within computational number theory Antonino Leonardis1 - Gianfranco d’Atri2 - Fabio Caldarola3 1 Department of Mathematics and Computer Science, University of Calabria Arcavacata di Rende, Italy e-mail: [email protected] 2 Department of Mathematics and Computer Science, University of Calabria Arcavacata di Rende, Italy 3 Department of Mathematics and Computer Science, University of Calabria Arcavacata di Rende, Italy e-mail: [email protected] Abstract Literature considers under the name unimaginable numbers any positive in- teger going beyond any physical application, with this being more of a vague description of what we are talking about rather than an actual mathemati- cal definition (it is indeed used in many sources without a proper definition). This simply means that research in this topic must always consider shortened representations, usually involving recursion, to even being able to describe such numbers. One of the most known methodologies to conceive such numbers is using hyper-operations, that is a sequence of binary functions defined recursively starting from the usual chain: addition - multiplication - exponentiation. arXiv:1901.05372v2 [cs.LO] 12 Mar 2019 The most important notations to represent such hyper-operations have been considered by Knuth, Goodstein, Ackermann and Conway as described in this work’s introduction. Within this work we will give an axiomatic setup for this topic, and then try to find on one hand other ways to represent unimaginable numbers, as well as on the other hand applications to computer science, where the algorith- mic nature of representations and the increased computation capabilities of 1 computers give the perfect field to develop further the topic, exploring some possibilities to effectively operate with such big numbers.
    [Show full text]
  • MPC5634M Microcontroller Data Sheet, Rev
    Freescale Semiconductor MPC5634M Rev. 9.2, 01/2015 MPC5634M Microcontroller Datasheet This is the MPC5634M Datasheet set consisting of the following files: • MPC5634M Datasheet Addendum (MPC5634M_AD), Rev. 1 • MPC5634M Datasheet (MPC5634M), Rev. 9 © Freescale Semiconductor, Inc., 2015. All rights reserved. Freescale Semiconductor MPC5634M_AD Datasheet Addendum Rev. 1.0, 01/2015 MPC5634M Microcontroller Datasheet Addendum This addendum describes corrections to the MPC5634M Table of Contents Microcontroller Datasheet, order number MPC5634M. 1 Addendum List for Revision 9 . 2 For convenience, the addenda items are grouped by 2 Revision History . 2 revision. Please check our website at http://www.freescale.com/powerarchitecture for the latest updates. The current version available of the MPC5634M Microcontroller Datasheet is Revision 9. © Freescale Semiconductor, Inc., 2015. All rights reserved. 1 Addendum List for Revision 9 4 Table 1. MPC5634M Rev 9 Addendum Location Description Section 4.11, “Temperature In “Temperature Sensor Electrical Characteristics” table, update the Min and Max value of Sensor Electrical “Accuracy” parameter to -20oC and +20oC, respectively. Characteristics”, Page 81 2 Revision History Table 2 provides a revision history for this datasheet addendum document. Table 2. Revision History Table Rev. Number Substantive Changes Date of Release 1.0 Initial release. 12/2014 MPC5634M_AD, Rev. 1.0 2 Freescale Semiconductor How to Reach Us: Information in this document is provided solely to enable system and software Home Page: implementers to use Freescale products. There are no express or implied copyright freescale.com licenses granted hereunder to design or fabricate any integrated circuits based on the Web Support: information in this document. freescale.com/support Freescale reserves the right to make changes without further notice to any products herein.
    [Show full text]
  • Multiplication Fact Strategies Assessment Directions and Analysis
    Multiplication Fact Strategies Wichita Public Schools Curriculum and Instructional Design Mathematics Revised 2014 KCCRS version Table of Contents Introduction Page Research Connections (Strategies) 3 Making Meaning for Operations 7 Assessment 9 Tools 13 Doubles 23 Fives 31 Zeroes and Ones 35 Strategy Focus Review 41 Tens 45 Nines 48 Squared Numbers 54 Strategy Focus Review 59 Double and Double Again 64 Double and One More Set 69 Half and Then Double 74 Strategy Focus Review 80 Related Equations (fact families) 82 Practice and Review 92 Wichita Public Schools 2014 2 Research Connections Where Do Fact Strategies Fit In? Adapted from Randall Charles Fact strategies are considered a crucial second phase in a three-phase program for teaching students basic math facts. The first phase is concept learning. Here, the goal is for students to understand the meanings of multiplication and division. In this phase, students focus on actions (i.e. “groups of”, “equal parts”, “building arrays”) that relate to multiplication and division concepts. An important instructional bridge that is often neglected between concept learning and memorization is the second phase, fact strategies. There are two goals in this phase. First, students need to recognize there are clusters of multiplication and division facts that relate in certain ways. Second, students need to understand those relationships. These lessons are designed to assist with the second phase of this process. If you have students that are not ready, you will need to address the first phase of concept learning. The third phase is memorization of the basic facts. Here the goal is for students to master products and quotients so they can recall them efficiently and accurately, and retain them over time.
    [Show full text]
  • Automated Synthesis of Symbolic Instruction Encodings from I/O Samples
    Automated Synthesis of Symbolic Instruction Encodings from I/O Samples Patrice Godefroid Ankur Taly Microsoft Research Stanford University PLDI’2012 Page 1 June 2012 Need for Symbolic Instruction Encodings Symbolic Execution is a key l 1 : m o v eax, i n p 1 component of precise binary m o v c l , i n p 2 program analysis tools s h l eax, c l j n z l2 j m p l3 - SAGE, BitBlaze, BAP, etc. l 2 : d i v ebx, eax // Is this safe ? - Static analysis tools / / I s e a x ! = 0 ? l 3 : … PLDI’2012 Page 2 June 2012 Problem: Symbolic Instruction Encoding Bit Vector[X] Instruction Bit Vector[Y] Inp 1 ? Op1 Inpn Opm Problem: Given a processor and an instruction name, symbolically describe the input-output function for the instruction • Express the encoding as bit-vector constraints (ex: SMT-Lib format) PLDI’2012 Page 3 June 2012 So far, only manual solutions… • From the instruction architecture manual (X86, ARM, …) implemented by the processor Limitations: • Tedious, expensive - X86 has more than 300 unique instructions, each with ~10 OPCodes, 2000 pages • Error-prone - Written in English, many corner cases • Imprecise - Spec is often under-specified • Partial - Not all instructions are covered X86 spec for SHLD • Can we trust the spec ? PLDI’2012 Page 4 June 2012 Here: Automated Synthesis Approach Searches for a function f that respects truth table Partial Truth- table S Sample inputs Synthesis Function (C with in-lined engine f assembly) Goals: • As automated as possible so that we can boot-strap a symbolic execution engine on an arbitrary instruction
    [Show full text]
  • Matrix Multiplication. Diagonal Matrices. Inverse Matrix. Matrices
    MATH 304 Linear Algebra Lecture 4: Matrix multiplication. Diagonal matrices. Inverse matrix. Matrices Definition. An m-by-n matrix is a rectangular array of numbers that has m rows and n columns: a11 a12 ... a1n a21 a22 ... a2n . .. . am1 am2 ... amn Notation: A = (aij )1≤i≤n, 1≤j≤m or simply A = (aij ) if the dimensions are known. Matrix algebra: linear operations Addition: two matrices of the same dimensions can be added by adding their corresponding entries. Scalar multiplication: to multiply a matrix A by a scalar r, one multiplies each entry of A by r. Zero matrix O: all entries are zeros. Negative: −A is defined as (−1)A. Subtraction: A − B is defined as A + (−B). As far as the linear operations are concerned, the m×n matrices can be regarded as mn-dimensional vectors. Properties of linear operations (A + B) + C = A + (B + C) A + B = B + A A + O = O + A = A A + (−A) = (−A) + A = O r(sA) = (rs)A r(A + B) = rA + rB (r + s)A = rA + sA 1A = A 0A = O Dot product Definition. The dot product of n-dimensional vectors x = (x1, x2,..., xn) and y = (y1, y2,..., yn) is a scalar n x · y = x1y1 + x2y2 + ··· + xnyn = xk yk . Xk=1 The dot product is also called the scalar product. Matrix multiplication The product of matrices A and B is defined if the number of columns in A matches the number of rows in B. Definition. Let A = (aik ) be an m×n matrix and B = (bkj ) be an n×p matrix.
    [Show full text]
  • Toshiba 32-Bit Arm Core-Based Microcontroller Product Guide
    SUBSIDIARIES AND AFFILIATES (As of July 1, 2017) Toshiba America Toshiba Electronics Europe GmbH Toshiba Electronics Asia, Ltd. Nov. 2017 Semiconductor Catalog Nov. 2017 Electronic Components, Inc. • Düsseldorf Head Office Tel: 2375-6111 Fax: 2375-0969 • Irvine, Headquarters Tel: (0211)5296-0 Fax: (0211)5296-400 Toshiba Electronics (China) Co., Ltd. BCE0085H Tel: (949)462-7700 Fax: (949)462-2200 • France Branch • Shanghai Head Office • Buffalo Grove (Chicago) Tel: (1)47282181 Tel: (021)6139-3888 Fax: (021)6190-8288 Tel: (847)484-2400 Fax: (847)541-7287 • Italy Branch • Beijing Branch • Duluth/Atlanta Tel: (039)68701 Fax:(039)6870205 Tel: (010)6590-8796 Fax: (010)6590-8791 Tel: (404)639-9520 Fax: (404)634-4434 • Munich Office • Chengdu Branch • El Paso Tel: (089)20302030 Fax: (089)203020310 Tel: (028)8675-1773 Fax: (028)8675-1065 Tel: (915)533-4242 • Spain Branch • Hangzhou Office • Marlborough Tel: (91)660-6794 Tel: (0571)8717-5004 Fax: (0571)8717-5013 Tel: (508)481-0034 Fax: (508)481-8828 • Sweden Branch • Nanjing Office • Parsippany Tel: (08)704-0900 Fax: (08)80-8459 Tel: (025)8689-0070 Fax: (025)5266-5106 Tel: (973)541-4715 Fax: (973)541-4716 • U.K. Branch • Qingdao Branch 32-Bit Microcontrollers 32-Bit Microcontrollers • San Jose Tel: (1932)841600 Tel: (532)8579-3328 Fax: (532)8579-3329 Tel: (408)526-2400 Fax: (408)526-2410 Toshiba Electronics Asia (Singapore) Pte. Ltd. • Shenzhen Branch • Wixom (Detroit) Tel: (65)6278-5252 Fax: (65)6271-5155 Tel: (0755)3686-0880 Fax: (0755)3686-0816 Tel: (248)347-2607 Fax: (248)347-2602 Toshiba Electronics Service (Thailand) Co., Ltd.
    [Show full text]
  • Multiplication and Divisions
    Third Grade Math nd 2 Grading Period Power Objectives: Academic Vocabulary: multiplication array Represent and solve problems involving multiplication and divisor commutative division. (P.O. #1) property Understand properties of multiplication and the distributive property relationship between multiplication and divisions. estimation division factor column (P.O. #2) Multiply and divide with 100. (P.O. #3) repeated addition multiple Solve problems involving the four operations, and identify associative property quotient and explain the patterns in arithmetic. (P.O. #4) rounding row product equation Multiplication and Division Enduring Understandings: Essential Questions: Mathematical operations are used in solving problems In what ways can operations affect numbers? in which a new value is produced from one or more How can different strategies be helpful when solving a values. problem? Algebraic thinking involves choosing, combining, and How does knowing and using algorithms help us to be applying effective strategies for answering questions. Numbers enable us to use the four operations to efficient problem solvers? combine and separate quantities. How are multiplication and addition alike? See below for additional enduring understandings. How are subtraction and division related? See below for additional essential questions. Enduring Understandings: Multiplication is repeated addition, related to division, and can be used to solve story problems. For a given set of numbers, there are relationships that
    [Show full text]