DOCSLIB.ORG

Episodes in the History of Modern Algebra (1800–1950)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Episodes in the History of Modern Algebra (1800–1950) HISTORY OF MATHEMATICS • VOLUME 32 Episodes in the History of Modern Algebra (1800–1950) Jeremy J. Gray Karen Hunger Parshall Editors American Mathematical Society • London Mathematical Society Episodes in the History of Modern Algebra (1800–1950) https://doi.org/10.1090/hmath/032 HISTORY OF MATHEMATICS v VOLUME 32 Episodes in the History of Modern Algebra (1800–1950) Jeremy J. Gray Karen Hunger Parshall Editors Editorial Board American Mathematical Society London Mathematical Society Joseph W. Dauben Alex D. D. Craik Peter Duren Jeremy J. Gray Karen Parshall, Chair Robin Wilson, Chair MichaelI.Rosen 2000 Mathematics Subject Classification. Primary 01A55, 01A60, 01A70, 01A72, 01A73, 01A74, 01A80. For additional information and updates on this book, visit www.ams.org/bookpages/hmath-32 Library of Congress Cataloging-in-Publication Data Episodes in the history of modern algebra (1800–1950) / Jeremy J. Gray and Karen Hunger Parshall, editors. p. cm. Includes bibliographical references and index. ISBN-13: 978-0-8218-4343-7 (alk. paper) ISBN-10: 0-8218-4343-5 (alk. paper) 1. Algebra—History. I. Gray, Jeremy, 1947– II. Parshall, Karen Hunger, 1955– QA151.E65 2007 512.009—dc22 2007060683 AMS softcover ISBN: 978-0-8218-6904-8 Copying and reprinting. Individual readers of this publication, and nonprofit libraries acting for them, are permitted to make fair use of the material, such as to copy a chapter for use in teaching or research. Permission is granted to quote brief passages from this publication in reviews, provided the customary acknowledgment of the source is given. Republication, systematic copying, or multiple reproduction of any material in this publication is permitted only under license from the American Mathematical Society. Requests for such permission should be addressed to the Acquisitions Department, American Mathematical Society, 201 Charles Street, Providence, Rhode Island 02904-2294 USA. Requests can also be made by e-mail to [email protected]. c 2007 by the American Mathematical Society. All rights reserved. Reprinted in softcover by the American Mathematical Society, 2011. Printed in the United States of America. Copyright of individual articles may revert to the public domain 28 years after publication. Contact the AMS for copyright status of individual articles. The American Mathematical Society retains all rights except those granted to the United States Government. ∞ The paper used in this book is acid-free and falls within the guidelines established to ensure permanence and durability. The London Mathematical Society is incorporated under Royal Charter and is registered with the Charity Commissioners. Visit the AMS home page at http://www.ams.org/ 10987654321 161514131211 Contents Acknowledgments 1 Chapter 1. Introduction Jeremy J. Gray and Karen Hunger Parshall 3 Algebra: What? When? Where? 3 Episodes in the History of Modern Algebra 5 Concluding Remarks 10 References 10 Chapter 2. Babbage and French Id´eologie: Functional Equations, Language, and the Analytical Method Eduardo L. Ortiz 13 Introduction 13 Speculation on the Origin of Languages 14 Senses, Languages, and the Elaboration of a Theory of Signs 16 The Position of Grammar 17 On the Language of Calculation 18 Babbage and a “Language” for the Solution of Functional Equations 19 Babbage’s Notation 21 Babbage’s Treatment of Functional Equations 23 Babbage and First-Order Functional Equations in One Variable 26 The Aftermath of Condillac in France: The Beginning of a Discussion 28 De G´erando’s Critique of Condillac: A Turning Point in Id´eologie 31 De G´erando’s Theory of Signs and Its Mathematical Implications 33 Babbage and de G´erando’s Views on Signs 36 Destutt de Tracy’s El´´ emens d’id´eologie 37 Destutt de Tracy’s Views on Artificial Languages 39 Final Remarks 40 References 42 Chapter 3. “Very Full of Symbols”: Duncan F. Gregory, the Calculus of Operations, and the Cambridge Mathematical Journal Sloan Evans Despeaux 49 Introduction 49 The Establishment of a “Proper Channel” for the Research of Junior British Mathematicians 50 The Calculus of Operations before the Cambridge Mathematical Journal 52 The Revival: The Introduction of the Calculus of Operations into the Cambridge Mathematical Journal 54 v vi CONTENTS The Conversation Begins: The Adoption of the Calculus of Operations by Contributors to the Cambridge Mathematical Journal 60 Conclusion 67 References 69 Chapter 4. Divisibility Theories in the Early History of Commutative Algebra and the Foundations of Algebraic Geometry Olaf Neumann 73 On Some Developments Rooted in the Eighteenth Century 74 Developments Inspired by Gauss 77 From Kummer to Zolotarev 84 Complex Analytic and Algebraic Functions 87 Kronecker’s Modular Systems 89 The Work of David Hilbert and Emanuel Lasker 94 The Work of Emmy Noether and Her Successors 97 Concluding Remarks 99 References 100 Chapter 5. Kronecker’s Fundamental Theorem of General Arithmetic Harold M. Edwards 107 Introduction 107 Statement and Proof of Kronecker’s Theorem 109 Conclusions 114 References 115 Chapter 6. Developments in the Theory of Algebras over Number Fields: A New Foundation for the Hasse Norm Residue Symbol and New Approaches to Both the Artin Reciprocity Law and Class Field Theory Gunther¨ Frei 117 Introduction 117 The Beginnings of Structure Theory 118 Wedderburn’s General Structure Theorems 121 Hurwitz and the Arithmetic of Quaternions 122 The Structure of Skew Fields: Connections with Algebraic Number Theory 124 The Theory of Semisimple Algebras 127 The Local Theory and the Theorem of Brauer-Hasse-Noether 133 The New Norm Residue Symbol and New Approaches to Both the Reciprocity Law and Class Field Theory 135 Summary and Conclusions 141 References 143 Chapter 7. Minkowski, Hensel, and Hasse: On The Beginnings of the Local-Global Principle Joachim Schwermer 153 Introduction 153 Toward an Arithmetic Theory of Quadratic Forms 155 Mathematical Digression: Quadratic Forms over Rings 158 Hermann Minkowski’s Early Work 159 Hermann Minkowski’s Letter to Adolf Hurwitz in 1890 161 CONTENTS vii Hensel’s p-adic Numbers: Series, Expansions, or Numbers as Functions 162 Mathematical Digression: Valuations and p-adic Fields 164 Hasse’s Thesis and Habilitationsschrift 165 From the Small to the Large, or a Local-Global Principle 167 A Talk by Hasse in K¨onigsberg in 1936 168 Conclusion 170 Appendix: Helmut Hasse to Hermann Weyl, 15 December, 1931 171 References 173 Chapter 8. Research in Algebra at the University of Chicago: Leonard Eugene Dickson and A. Adrian Albert Della Dumbaugh Fenster 179 Introduction 179 Leonard Dickson: Student 179 Leonard Dickson: University of Chicago Faculty Member 180 A. Adrian Albert and the Classification of Division Algebras 181 A. Adrian Albert: Professional Overview 188 Conclusions 192 References 194 Chapter 9. Emmy Noether’s 1932 ICM Lecture on Noncommutative Methods in Algebraic Number Theory Charles W. Curtis 199 Introduction 199 Brauer’s Factor Sets, the Brauer Group, and Crossed Products 202 Cyclic Algebras and the Albert-Brauer-Hasse-Noether Theorem 206 The Principal Genus Theorem 210 Applications to Algebraic Number Theory by Hasse and Chevalley 212 Conclusion 215 References 217 Chapter 10. From Algebra (1895) to Moderne Algebra (1930): Changing Conceptions of a Discipline–A Guided Tour Using the Jahrbuch uber¨ die Fortschritte der Mathematik Leo Corry 221 Introduction 221 The Jahrbuchuber ¨ die Fortschritte der Mathematik 225 Algebra by the Turn of the Century: The Jahrbuch in 1900 227 Some Tentative Changes: 1905–1915 229 Transactions of the American Mathematical Society: 1910 232 The Jahrbuch after 1916 233 Concluding Remarks 237 References 239 Chapter 11. A Historical Sketch of B. L. van der Waerden’s Work in Algebraic Geometry: 1926–1946 Norbert Schappacher 245 Introduction 245 1925: Algebraizing Algebraic Geometry `alaEmmy Noether 250 1927–1932: Forays into Intersection Theory 256 viii CONTENTS 1933–1939: When in Rome . ? 264 1933–1946: The Construction Site of Algebraic Geometry 272 Appendix: Extract from a Letter from Hasse to Severi 276 References 278 Chapter 12. On the Arithmetization of Algebraic Geometry Silke Slembek 285 Introduction 285 Earlier Rewritings of Algebraic Geometry 286 The Mathematical Situation: Why Another Rewriting Seemed Necessary 289 Imitating Geometry with Modern Algebra and Arithmetic Ideal Theory 292 Leaving the Beaten Path 294 The Arithmetic Proof 296 Conclusion 296 References 298 Chapter 13. The Rising Sea: Grothendieck on Simplicity and Generality Colin McLarty 301 The Weil Conjectures 303 Abelian Categories 305 The Larger Vision 311 Anticipations of Schemes 313 Schemes in Paris 315 Schemes in Grothendieck 317 Toward the S´eminaire de G´eom´etrie Alg´ebrique 321 References 322 Index 327 Index Abel, Niels Henrik, 4, 76 internationalization of, 192 as father of the theory of algebraic func- Kronecker’s views on the foundations of, tions, 87 107–109 on the solution of algebraic equations, 111 origin of the term, 3 Abelian categories, 305–311 Peacock’s views on, 58–59 Abelian functions research in around 1800, 74 Riemann’s work on, 87–88 the role of the calculus of operations in theory of, 87–88 the development of in Britain, 68 al-Khw¯arizm¯ı, 3 Algebraic functions Albert, A. Adrian Abel as father of, 87 as an adviser, 190 Dedekind’s work on, 88–89 broader community interests of, 189–190 E. Noether’s work on, 89 career of, 188–192 Kronecker’s work on, 88 correspondence of with Hasse, 184–187 theory of, 87–89 early education of, 181–183 Weber’s work on, 88–89 joint paper
Load more

Recommended publications
  • Hasse Principles for Higher-Dimensional Fields 3
    Annals of Mathematics 183 (2016), 1{71 http://dx.doi.org/10.4007/annals.2016.183.1.1 Hasse principles for higher-dimensional fields By Uwe Jannsen dedicated to J¨urgen Neukirch Abstract For rather general excellent schemes X, K. Kato defined complexes of Gersten-Bloch-Ogus type involving the Galois cohomology groups of all residue fields of X. For arithmetically interesting schemes, he developed a fascinating web of conjectures on some of these complexes, which generalize the classical Hasse principle for Brauer groups over global fields, and proved these conjectures for low dimensions. We prove Kato's conjecture over number fields in any dimension. This gives a cohomological Hasse principle for function fields F over a number field K, involving the corresponding function fields Fv over the completions Kv of K. For global function fields K we prove the part on injectivity for coefficients invertible in K. Assuming resolution of singularities, we prove a similar conjecture of Kato over finite fields, and a generalization to arbitrary finitely generated fields. Contents 0. Introduction1 1. First reductions and a Hasse principle for global fields7 2. Injectivity of the global-local map for coefficients invertible in K 16 3. A crucial exact sequence, and a Hasse principle for unramified cohomology 26 4. A Hasse principle for Bloch-Ogus-Kato complexes 40 5. Weight complexes and weight cohomology 52 References 67 0. Introduction In this paper we prove some conjectures of K. Kato [Kat86] which were formulated to generalize the classical exact sequence of Brauer groups for a global field K, L (0.1) 0 −! Br(K) −! Br(Kv) −! Q=Z −! 0; v c 2016 Department of Mathematics, Princeton University.
    [Show full text]
  • Lesson 2: the Multiplication of Polynomials
    NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 2 M1 ALGEBRA II Lesson 2: The Multiplication of Polynomials Student Outcomes . Students develop the distributive property for application to polynomial multiplication. Students connect multiplication of polynomials with multiplication of multi-digit integers. Lesson Notes This lesson begins to address standards A-SSE.A.2 and A-APR.C.4 directly and provides opportunities for students to practice MP.7 and MP.8. The work is scaffolded to allow students to discern patterns in repeated calculations, leading to some general polynomial identities that are explored further in the remaining lessons of this module. As in the last lesson, if students struggle with this lesson, they may need to review concepts covered in previous grades, such as: The connection between area properties and the distributive property: Grade 7, Module 6, Lesson 21. Introduction to the table method of multiplying polynomials: Algebra I, Module 1, Lesson 9. Multiplying polynomials (in the context of quadratics): Algebra I, Module 4, Lessons 1 and 2. Since division is the inverse operation of multiplication, it is important to make sure that your students understand how to multiply polynomials before moving on to division of polynomials in Lesson 3 of this module. In Lesson 3, division is explored using the reverse tabular method, so it is important for students to work through the table diagrams in this lesson to prepare them for the upcoming work. There continues to be a sharp distinction in this curriculum between justification and proof, such as justifying the identity (푎 + 푏)2 = 푎2 + 2푎푏 + 푏 using area properties and proving the identity using the distributive property.
    [Show full text]
  • Conics Over Function Fields and the Artin-Tate Conjecture José Felipe
    Conics over function fields and the Artin-Tate conjecture Jos´eFelipe Voloch Abstract: We prove that the Hasse principle for conics over function fields is a simple consequence of a provable case of the Artin-Tate conjecture for surfaces over finite fields. Hasse proved that a conic over a global field has a rational point if and only if it has points over all completions of the global field, an instance of the so-called local-global or Hasse principle. The case of the rational numbers is an old result of Legendre, who gave an elementary proof and a similar proof can be given in the case of rational functions over a finite field. Hasse’s proof, on the other hand, is a consequence of a more general result in Class Field Theory, the Hasse norm theorem. One purpose of this paper is to give a new proof of the local-global principle for conics over function fields, as a relatively simple consequence of a provable case of the Artin-Tate conjecture for surfaces over finite fields. This proof might be more complicated overall, once the work on the Artin-Tate conjecture is factored in, but it might be worthwhile recording since it suggests a new approach to local-global principles which might work in other contexts, such as number fields or higher dimensions. We also deduce from the Artin-Tate conjecture, together with a recent result [LLR] on Brauer groups, the Hilbert reciprocity law. We also do a careful study of conic bundles over curves over finite fields which might have independent interest.
    [Show full text]
  • Counterexamples to the Hasse Principle
    COUNTEREXAMPLES TO THE HASSE PRINCIPLE W. AITKEN AND F. LEMMERMEYER Abstract. This article explains the Hasse principle and gives a self-contained development of certain counterexamples to this principle. The counterexam- ples considered are similar to the earliest counterexample discovered by Lind and Reichardt. This type of counterexample is important in the theory of elliptic curves: today they are interpreted as nontrivial elements in Tate– Shafarevich groups. 1. Introduction In this article we develop counterexamplestotheHasseprincipleusingonlytech- niques from undergraduate number theory and algebra. By keeping the technical prerequisites to a minimum, we hope to provide a path for nonspecialists to this interesting area of number theory. The counterexamples considered here extend the classical counterexample of Lind and Reichardt. As discussed in an appendix, such counterexamples are important in the theory of elliptic curves, and today are interpreted as nontrivial elements in Tate–Shafarevich groups. 2. Background The problem of determining if the Diophantine equation aX2 + bY 2 + cZ2 =0 (1) has nontrivial solutions with values in Z has played a prominent role in the history of number theory. We assume that a, b, and c are nonzero integers and, using a simple argument, we reduce to the case where the product abc is square-free. Lagrange (1768) solved the problem by giving a descent procedure which determines in a finite number of steps whether or not (1) has a nontrivial Z-solution, but Legendre (1788) gave the definitive solution. Legendre proved that the following conditions, known by Euler to be necessary, are sufficient for the existence of a nontrivial Z- solution: (i) a, b,andc do not all have the same sign, and (ii) ab is a square modulo c , ca is a square modulo b ,and bc is a square modulo− a .
    [Show full text]
  • Algebraic Tori — Thirty Years After
    ALGEBRAIC TORI | THIRTY YEARS AFTER BORIS KUNYAVSKI˘I To my teacher Valentin Evgenyevich Voskresenski˘ı, with gratitude and admiration This article is an expanded version of my talk given at the Interna- tional Conference \Algebra and Number Theory" dedicated to the 80th anniversary of V. E. Voskresenski˘ı, which was held at the Samara State University in May 2007. The goal is to give an overview of results of V. E. Voskresenski˘ı on arithmetic and birational properties of algebraic tori which culminated in his monograph [Vo77] published 30 years ago. I shall try to put these results and ideas into somehow broader context and also to give a brief digest of the relevant activity related to the period after the English version of the monograph [Vo98] appeared. 1. Rationality and nonrationality problems A classical problem, going back to Pythagorean triples, of describing the set of solutions of a given system of polynomial equations by ratio- nal functions in a certain number of parameters (rationality problem) has been an attraction for many generations. Although a lot of various techniques have been used, one can notice that after all, to establish rationality, one usually has to exhibit some explicit parameterization such as that obtained by stereographic projection in the Pythagoras problem. The situation is drastically different if one wants to estab- lish non-existence of such a parameterization (nonrationality problem): here one usually has to use some known (or even invent some new) bi- rational invariant allowing one to detect nonrationality by comparing its value for the object under consideration with some \standard" one known to be zero; if the computation gives a nonzero value, we are done.
    [Show full text]
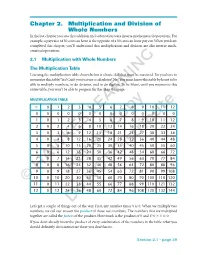
  • Chapter 2. Multiplication and Division of Whole Numbers in the Last Chapter You Saw That Addition and Subtraction Were Inverse Mathematical Operations
    Chapter 2. Multiplication and Division of Whole Numbers In the last chapter you saw that addition and subtraction were inverse mathematical operations. For example, a pay raise of 50 cents an hour is the opposite of a 50 cents an hour pay cut. When you have completed this chapter, you’ll understand that multiplication and division are also inverse math- ematical operations. 2.1 Multiplication with Whole Numbers The Multiplication Table Learning the multiplication table shown below is a basic skill that must be mastered. Do you have to memorize this table? Yes! Can’t you just use a calculator? No! You must know this table by heart to be able to multiply numbers, to do division, and to do algebra. To be blunt, until you memorize this entire table, you won’t be able to progress further than this page. MULTIPLICATION TABLE ϫ 012 345 67 89101112 0 000 000LEARNING 00 000 00 1 012 345 67 89101112 2 024 681012Copy14 16 18 20 22 24 3 036 9121518212427303336 4 0481216 20 24 28 32 36 40 44 48 5051015202530354045505560 6061218243036424854606672Distribute 7071421283542495663707784 8081624324048566472808896 90918273HAWKESReview645546372819099108 10 0 10 20 30 40 50 60 70 80 90 100 110 120 ©11 0 11 22 33 44NOT 55 66 77 88 99 110 121 132 12 0 12 24 36 48 60 72 84 96 108 120 132 144 Do Let’s get a couple of things out of the way. First, any number times 0 is 0. When we multiply two numbers, we call our answer the product of those two numbers.
    [Show full text]
  • Grade 7/8 Math Circles the Scale of Numbers Introduction
    Faculty of Mathematics Centre for Education in Waterloo, Ontario N2L 3G1 Mathematics and Computing Grade 7/8 Math Circles November 21/22/23, 2017 The Scale of Numbers Introduction Last week we quickly took a look at scientific notation, which is one way we can write down really big numbers. We can also use scientific notation to write very small numbers. 1 × 103 = 1; 000 1 × 102 = 100 1 × 101 = 10 1 × 100 = 1 1 × 10−1 = 0:1 1 × 10−2 = 0:01 1 × 10−3 = 0:001 As you can see above, every time the value of the exponent decreases, the number gets smaller by a factor of 10. This pattern continues even into negative exponent values! Another way of picturing negative exponents is as a division by a positive exponent. 1 10−6 = = 0:000001 106 In this lesson we will be looking at some famous, interesting, or important small numbers, and begin slowly working our way up to the biggest numbers ever used in mathematics! Obviously we can come up with any arbitrary number that is either extremely small or extremely large, but the purpose of this lesson is to only look at numbers with some kind of mathematical or scientific significance. 1 Extremely Small Numbers 1. Zero • Zero or `0' is the number that represents nothingness. It is the number with the smallest magnitude. • Zero only began being used as a number around the year 500. Before this, ancient mathematicians struggled with the concept of `nothing' being `something'. 2. Planck's Constant This is the smallest number that we will be looking at today other than zero.
    [Show full text]
  • License Or Copyright Restrictions May Apply to Redistribution; See Https
    License or copyright restrictions may apply to redistribution; see https://www.ams.org/journal-terms-of-use License or copyright restrictions may apply to redistribution; see https://www.ams.org/journal-terms-of-use EMIL ARTIN BY RICHARD BRAUER Emil Artin died of a heart attack on December 20, 1962 at the age of 64. His unexpected death came as a tremendous shock to all who knew him. There had not been any danger signals. It was hard to realize that a person of such strong vitality was gone, that such a great mind had been extinguished by a physical failure of the body. Artin was born in Vienna on March 3,1898. He grew up in Reichen- berg, now Tschechoslovakia, then still part of the Austrian empire. His childhood seems to have been lonely. Among the happiest periods was a school year which he spent in France. What he liked best to remember was his enveloping interest in chemistry during his high school days. In his own view, his inclination towards mathematics did not show before his sixteenth year, while earlier no trace of mathe­ matical aptitude had been apparent.1 I have often wondered what kind of experience it must have been for a high school teacher to have a student such as Artin in his class. During the first world war, he was drafted into the Austrian Army. After the war, he studied at the University of Leipzig from which he received his Ph.D. in 1921. He became "Privatdozent" at the Univer­ sity of Hamburg in 1923.
    [Show full text]
  • Cohomological Hasse Principle and Motivic Cohomology for Arithmetic Schemes
    COHOMOLOGICAL HASSE PRINCIPLE AND MOTIVIC COHOMOLOGY FOR ARITHMETIC SCHEMES by MORITZ KERZ and SHUJI SAITO ABSTRACT In 1985 Kazuya Kato formulated a fascinating framework of conjectures which generalizes the Hasse principle for the Brauer group of a global field to the so-called cohomological Hasse principle for an arithmetic scheme X. In this paper we prove the prime-to-characteristic part of the cohomological Hasse principle. We also explain its implications on finiteness of motivic cohomology and special values of zeta functions. CONTENTS Introduction........................................................ 123 1.Homologytheory................................................... 129 2.Log-pairsandconfigurationcomplexes....................................... 135 3.Lefschetzcondition.................................................. 140 4.Pullbackmap(firstconstruction)........................................... 146 5.Pullbackmap(secondconstruction)......................................... 159 6.Maintheorem..................................................... 162 7.Resultwithfinitecoefficients............................................. 166 8.Kato’sconjectures................................................... 169 9.Applicationtocyclemaps............................................... 174 10.Applicationtospecialvaluesofzetafunctions.................................... 176 Acknowledgements..................................................... 178 Appendix A: Galois cohomology with compact support . .............................. 179 References........................................................
    [Show full text]
  • Mathematicians Fleeing from Nazi Germany
    Mathematicians Fleeing from Nazi Germany Mathematicians Fleeing from Nazi Germany Individual Fates and Global Impact Reinhard Siegmund-Schultze princeton university press princeton and oxford Copyright 2009 © by Princeton University Press Published by Princeton University Press, 41 William Street, Princeton, New Jersey 08540 In the United Kingdom: Princeton University Press, 6 Oxford Street, Woodstock, Oxfordshire OX20 1TW All Rights Reserved Library of Congress Cataloging-in-Publication Data Siegmund-Schultze, R. (Reinhard) Mathematicians fleeing from Nazi Germany: individual fates and global impact / Reinhard Siegmund-Schultze. p. cm. Includes bibliographical references and index. ISBN 978-0-691-12593-0 (cloth) — ISBN 978-0-691-14041-4 (pbk.) 1. Mathematicians—Germany—History—20th century. 2. Mathematicians— United States—History—20th century. 3. Mathematicians—Germany—Biography. 4. Mathematicians—United States—Biography. 5. World War, 1939–1945— Refuges—Germany. 6. Germany—Emigration and immigration—History—1933–1945. 7. Germans—United States—History—20th century. 8. Immigrants—United States—History—20th century. 9. Mathematics—Germany—History—20th century. 10. Mathematics—United States—History—20th century. I. Title. QA27.G4S53 2008 510.09'04—dc22 2008048855 British Library Cataloging-in-Publication Data is available This book has been composed in Sabon Printed on acid-free paper. ∞ press.princeton.edu Printed in the United States of America 10 987654321 Contents List of Figures and Tables xiii Preface xvii Chapter 1 The Terms “German-Speaking Mathematician,” “Forced,” and“Voluntary Emigration” 1 Chapter 2 The Notion of “Mathematician” Plus Quantitative Figures on Persecution 13 Chapter 3 Early Emigration 30 3.1. The Push-Factor 32 3.2. The Pull-Factor 36 3.D.
    [Show full text]
  • Counterexamples to the Local-Global Principle for Non-Singular Plane Curves and a Cubic Analogue of Ankeny-Artin-Chowla-Mordell Conjecture
    COUNTEREXAMPLES TO THE LOCAL-GLOBAL PRINCIPLE FOR NON-SINGULAR PLANE CURVES AND A CUBIC ANALOGUE OF ANKENY-ARTIN-CHOWLA-MORDELL CONJECTURE YOSHINOSUKE HIRAKAWA AND YOSUKE SHIMIZU Abstract. In this article, we introduce a systematic and uniform construction of non- singular plane curves of odd degrees n ≥ 5 which violate the local-global principle. Our construction works unconditionally for n divisible by p2 for some odd prime number p. Moreover, our construction also works for n divisible by some p ≥ 5 which satisfies 1=3 1=3 a conjecture on p-adic properties of the fundamental units of Q(p ) and Q((2p) ). This conjecture is a natural cubic analogue of the classical Ankeny-Artin-Chowla-Mordell 1=2 conjecture for Q(p ) and easily verified numerically. 1. Introduction In the theory of Diophantine equations, the local-global principle for quadratic forms established by Minkowski and Hasse is one of the major culminations (cf. [31, Theorem 8, Ch. IV]). In contrast, there exist many homogeneous forms of higher degrees which violate the local-global principle (i.e., counterexamples to the local-global principle). For example, Selmer [30] found that a non-singular plane cubic curve defined by (1) 3X3 + 4Y 3 = 5Z3 has rational points over R and Qp for every prime number p but not over Q. From eq. (1), we can easily construct reducible (especially singular) counterexamples of higher degrees. After that, Fujiwara [13] found that a non-singular plane quintic curve defined by (2) (X3 + 5Z3)(X2 + XY + Y 2) = 17Z5 violates the local-global principle. More recently, Cohen [9, Corollary 6.4.11] gave several p p p counterexamples of the form x + by + cz = 0 of degree p = 3; 5; 7; 11 with b; c 2 Z, and Nguyen [23, 24] gave recipes for counterexamples of even degrees and more complicated forms.
    [Show full text]
  • The Notion Of" Unimaginable Numbers" in Computational Number Theory
    Beyond Knuth’s notation for “Unimaginable Numbers” within computational number theory Antonino Leonardis1 - Gianfranco d’Atri2 - Fabio Caldarola3 1 Department of Mathematics and Computer Science, University of Calabria Arcavacata di Rende, Italy e-mail: [email protected] 2 Department of Mathematics and Computer Science, University of Calabria Arcavacata di Rende, Italy 3 Department of Mathematics and Computer Science, University of Calabria Arcavacata di Rende, Italy e-mail: [email protected] Abstract Literature considers under the name unimaginable numbers any positive in- teger going beyond any physical application, with this being more of a vague description of what we are talking about rather than an actual mathemati- cal definition (it is indeed used in many sources without a proper definition). This simply means that research in this topic must always consider shortened representations, usually involving recursion, to even being able to describe such numbers. One of the most known methodologies to conceive such numbers is using hyper-operations, that is a sequence of binary functions defined recursively starting from the usual chain: addition - multiplication - exponentiation. arXiv:1901.05372v2 [cs.LO] 12 Mar 2019 The most important notations to represent such hyper-operations have been considered by Knuth, Goodstein, Ackermann and Conway as described in this work’s introduction. Within this work we will give an axiomatic setup for this topic, and then try to find on one hand other ways to represent unimaginable numbers, as well as on the other hand applications to computer science, where the algorith- mic nature of representations and the increased computation capabilities of 1 computers give the perfect field to develop further the topic, exploring some possibilities to effectively operate with such big numbers.
    [Show full text]