DOCSLIB.ORG

The Formal Rules of Algebra

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Formal Rules of Algebra The Formal Rules of Algebra Summary of the formal rules of algebra on the set of real numbers 1. The axioms of "equality" a = a Reflexive or Identity If a = b, then b = a. Symmetry If a = b and b = c, then a = c. Transitivity These are the "rules" that govern the use of the = sign. 2. The commutative rules of addition and multiplication + = + 풂 · 풃 = 풃· 풂 3. The associative풂 rules풃 of풃 addition풂 and multiplication ( + ) + = + ( + ) ( ) ( ) 풂 × 풃 × 풄 = 풂 × 풃× 풄 4. The identity풂 elements풃 풄 of addition풂 풃 and풄 multiplication: + = + = 풂 · ퟎ= ퟎ· =풂 풂 0 and 1are풂 theퟏ identityퟏ elements풂 풂 for addition and multiplication respectively 5. The additive inverse of a is −a + ( ) = + = 6. The multiplicative inverse or 풂reciprocal−풂 of a− is풂 symbolized풂 ퟎ as (a 0) ퟏ 풂 × = = , The product of a number and its reciprocal is 1 ퟏ 풂 Two풂 numbers풂 풂 areퟏ called reciprocals of one another if their product is 1. 1/a and a are reciprocal to each other. The reciprocal of p/q is q/p. 7. The algebraic definition of subtraction = + ( ) Subtraction, in algebra, is defined풂 as− addition풃 풂 of the− inverse풃 . 1 8. The algebraic definition of division ÷ = = × , 풂 ퟏ Division,풂 풃 in algebra,풃 풂 is defined풃 풃 ≠ asퟎ multiplication by the reciprocal. Hence, algebra has two fundamental operations: addition and multiplication. 9. The inverse of the inverse ( ) = 10. The− relationship−풂 풂 of = ( 풃 − 풂) 풕풐 풂 − 풃 11. The풃 Rule− 풂of Signs− for풂 multiplication,− 풃 division, and fractions ( ) = . ( ) = . ( )( ) = . 풂 −=풃 =−풂풃 and− 풂 풃= − 풂풃 −풂 −풃 풂풃 풂 −풂 풂 −풂 풂 Note: "Like−풃 signs풃 produce− 풃 a positive−풃 number;풃 unlike signs, a negative number." 12. Rules for 0 · = · = If풂 ퟎ , thenퟎ 풂= ,ퟎ but is not defined ퟎ 풂 풂 ≠ ퟎ 풂 ퟎ ퟎ 13. Multiplying/Factoring ( + ) = + The distributive rule/ Common factor 14. The풎 same풂 operation풃 on풎풂 both sides풎풃 of an equation If = , then + = + If = , then = 풂 풃 풂 풄 풃 풄 We may풂 add풃 the same풂풄 number to풃풄 both sides of an equation; we may multiply both sides by the same number. 15. Change of sign on both sides of an equation If = , then = . We may change−풂 every풃 sign on풂 both sides−풃 of an equation. 2 16. Change of sign on both sides of an inequality: Change of direction (sense) If < , then > . When풂 we change풃 the− 풂signs on− both풃 sides of an inequality, we must change the direction (sense) of the inequality. 17. The Four Forms of equations corresponding to the 16. Four Operations and their inverses If + = , then = . If – = , then = + . 풙 풂 풃 풙 풃 − 풂 If = , then = 풙 풂 풃 풙 풂 풃 풃 If 풂풙 = 풃 , then 풙 = �풂 18. Change풙 of sense when solving an inequality ⁄풂 풃 풙 풂풃 If < , then > 풃 19. Multiplication−풂풙 of풃 fractions 풙 − 풂 × = and × = 풂 풄 풂풄 풄 풂풄 20. Division풃 풅 of fractions풃풅 풂 (Complex풅 풅 fractions) ÷ = × = or equivalently 풂 풄 풂 풅 풂풅 Division풃 풅 is multiplication풃 풄 풃풄 by the reciprocal. 21. Addition/Subtraction of fractions ± ± = Same denominator 풂 풃 풂 풃 풄 풄 풄 ± ± = Different denominators 풂 풃 풂풅 풃풄 풄 풅 풄풅 22. Power and exponents Let n be a natural number, then = × × × . × 풏 풂 풂����풂���풂��������풂 풏−풇풂풄풕풐풓풔 Here, is called power, n is called exponent and a the 풏 풂 3 Laws of Exponents Laws Examples 1) = = ퟏ ퟏ 2) 풙 = 풙 ퟔ = ퟔ ퟎ ퟎ 3) 풙 =ퟏ / ퟕ =ퟏ / −ퟏ −ퟏ 4) 풙 =ퟏ 풙 ퟒ =ퟏ ퟒ = 풎 풏 풎+풏 ퟐ ퟑ ퟐ+ퟑ ퟓ 5) 풙 풙/ =풙 풙 풙/ =풙 =풙 풎 풏 풎−풏 ퟔ ퟐ ퟔ−ퟐ ퟒ × 6) (풙 )풙 = 풙 풙( )풙 = 풙 = 풙 풎 풏 풎풏 ퟐ ퟑ ퟐ ퟑ ퟔ 풙 풙 풙 풙 풙 7) ( ) = ( ) = 풏 풏 풏 ퟑ ퟑ ퟑ 풙풚 풙 풚 풙풚 풙 풚 8) ( / ) = / ( / ) = / 풏 풏 풏 ퟐ ퟐ ퟐ 풙 풚 풙 풚 풙 풚 풙 풚 9) = / = / −풏 풏 −ퟑ ퟑ 풙 ퟏ 풙 풙 ퟏ 풙 And the Laws about Fractional Exponents: / / 10) = = 풏 ퟑ ퟏ 풏 ퟏ ퟑ = = = = 11) 풙 풎 풙 풙ퟐ 풙 풏 √ 풏 풎 ퟑ √ ퟑ ퟐ 풏 풎 ퟑ ퟐ 풙 √풙 �√풙� 풙 √풙 �√풙� = = Proof of 11): 풎 follows from the fact that 풏 풏 풎 풏 풎 풙 = √×풙 ( / )�=√풙( �/ ) × 풎 풏 풎 ퟏ 풏 ퟏ 풏 풎 4 .
Load more

Recommended publications
  • 2.1 the Algebra of Sets
    Chapter 2 I Abstract Algebra 83 part of abstract algebra, sets are fundamental to all areas of mathematics and we need to establish a precise language for sets. We also explore operations on sets and relations between sets, developing an “algebra of sets” that strongly resembles aspects of the algebra of sentential logic. In addition, as we discussed in chapter 1, a fundamental goal in mathematics is crafting articulate, thorough, convincing, and insightful arguments for the truth of mathematical statements. We continue the development of theorem-proving and proof-writing skills in the context of basic set theory. After exploring the algebra of sets, we study two number systems denoted Zn and U(n) that are closely related to the integers. Our approach is based on a widely used strategy of mathematicians: we work with specific examples and look for general patterns. This study leads to the definition of modified addition and multiplication operations on certain finite subsets of the integers. We isolate key axioms, or properties, that are satisfied by these and many other number systems and then examine number systems that share the “group” properties of the integers. Finally, we consider an application of this mathematics to check digit schemes, which have become increasingly important for the success of business and telecommunications in our technologically based society. Through the study of these topics, we engage in a thorough introduction to abstract algebra from the perspective of the mathematician— working with specific examples to identify key abstract properties common to diverse and interesting mathematical systems. 2.1 The Algebra of Sets Intuitively, a set is a “collection” of objects known as “elements.” But in the early 1900’s, a radical transformation occurred in mathematicians’ understanding of sets when the British philosopher Bertrand Russell identified a fundamental paradox inherent in this intuitive notion of a set (this paradox is discussed in exercises 66–70 at the end of this section).
    [Show full text]
  • Db Math Marco Zennaro Ermanno Pietrosemoli Goals
    dB Math Marco Zennaro Ermanno Pietrosemoli Goals ‣ Electromagnetic waves carry power measured in milliwatts. ‣ Decibels (dB) use a relative logarithmic relationship to reduce multiplication to simple addition. ‣ You can simplify common radio calculations by using dBm instead of mW, and dB to represent variations of power. ‣ It is simpler to solve radio calculations in your head by using dB. 2 Power ‣ Any electromagnetic wave carries energy - we can feel that when we enjoy (or suffer from) the warmth of the sun. The amount of energy received in a certain amount of time is called power. ‣ The electric field is measured in V/m (volts per meter), the power contained within it is proportional to the square of the electric field: 2 P ~ E ‣ The unit of power is the watt (W). For wireless work, the milliwatt (mW) is usually a more convenient unit. 3 Gain and Loss ‣ If the amplitude of an electromagnetic wave increases, its power increases. This increase in power is called a gain. ‣ If the amplitude decreases, its power decreases. This decrease in power is called a loss. ‣ When designing communication links, you try to maximize the gains while minimizing any losses. 4 Intro to dB ‣ Decibels are a relative measurement unit unlike the absolute measurement of milliwatts. ‣ The decibel (dB) is 10 times the decimal logarithm of the ratio between two values of a variable. The calculation of decibels uses a logarithm to allow very large or very small relations to be represented with a conveniently small number. ‣ On the logarithmic scale, the reference cannot be zero because the log of zero does not exist! 5 Why do we use dB? ‣ Power does not fade in a linear manner, but inversely as the square of the distance.
    [Show full text]
  • The Five Fundamental Operations of Mathematics: Addition, Subtraction
    The five fundamental operations of mathematics: addition, subtraction, multiplication, division, and modular forms Kenneth A. Ribet UC Berkeley Trinity University March 31, 2008 Kenneth A. Ribet Five fundamental operations This talk is about counting, and it’s about solving equations. Counting is a very familiar activity in mathematics. Many universities teach sophomore-level courses on discrete mathematics that turn out to be mostly about counting. For example, we ask our students to find the number of different ways of constituting a bag of a dozen lollipops if there are 5 different flavors. (The answer is 1820, I think.) Kenneth A. Ribet Five fundamental operations Solving equations is even more of a flagship activity for mathematicians. At a mathematics conference at Sundance, Robert Redford told a group of my colleagues “I hope you solve all your equations”! The kind of equations that I like to solve are Diophantine equations. Diophantus of Alexandria (third century AD) was Robert Redford’s kind of mathematician. This “father of algebra” focused on the solution to algebraic equations, especially in contexts where the solutions are constrained to be whole numbers or fractions. Kenneth A. Ribet Five fundamental operations Here’s a typical example. Consider the equation y 2 = x3 + 1. In an algebra or high school class, we might graph this equation in the plane; there’s little challenge. But what if we ask for solutions in integers (i.e., whole numbers)? It is relatively easy to discover the solutions (0; ±1), (−1; 0) and (2; ±3), and Diophantus might have asked if there are any more.
    [Show full text]
  • Lesson 2: the Multiplication of Polynomials
    NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 2 M1 ALGEBRA II Lesson 2: The Multiplication of Polynomials Student Outcomes . Students develop the distributive property for application to polynomial multiplication. Students connect multiplication of polynomials with multiplication of multi-digit integers. Lesson Notes This lesson begins to address standards A-SSE.A.2 and A-APR.C.4 directly and provides opportunities for students to practice MP.7 and MP.8. The work is scaffolded to allow students to discern patterns in repeated calculations, leading to some general polynomial identities that are explored further in the remaining lessons of this module. As in the last lesson, if students struggle with this lesson, they may need to review concepts covered in previous grades, such as: The connection between area properties and the distributive property: Grade 7, Module 6, Lesson 21. Introduction to the table method of multiplying polynomials: Algebra I, Module 1, Lesson 9. Multiplying polynomials (in the context of quadratics): Algebra I, Module 4, Lessons 1 and 2. Since division is the inverse operation of multiplication, it is important to make sure that your students understand how to multiply polynomials before moving on to division of polynomials in Lesson 3 of this module. In Lesson 3, division is explored using the reverse tabular method, so it is important for students to work through the table diagrams in this lesson to prepare them for the upcoming work. There continues to be a sharp distinction in this curriculum between justification and proof, such as justifying the identity (푎 + 푏)2 = 푎2 + 2푎푏 + 푏 using area properties and proving the identity using the distributive property.
    [Show full text]
  • A Quick Algebra Review
    A Quick Algebra Review 1. Simplifying Expressions 2. Solving Equations 3. Problem Solving 4. Inequalities 5. Absolute Values 6. Linear Equations 7. Systems of Equations 8. Laws of Exponents 9. Quadratics 10. Rationals 11. Radicals Simplifying Expressions An expression is a mathematical “phrase.” Expressions contain numbers and variables, but not an equal sign. An equation has an “equal” sign. For example: Expression: Equation: 5 + 3 5 + 3 = 8 x + 3 x + 3 = 8 (x + 4)(x – 2) (x + 4)(x – 2) = 10 x² + 5x + 6 x² + 5x + 6 = 0 x – 8 x – 8 > 3 When we simplify an expression, we work until there are as few terms as possible. This process makes the expression easier to use, (that’s why it’s called “simplify”). The first thing we want to do when simplifying an expression is to combine like terms. For example: There are many terms to look at! Let’s start with x². There Simplify: are no other terms with x² in them, so we move on. 10x x² + 10x – 6 – 5x + 4 and 5x are like terms, so we add their coefficients = x² + 5x – 6 + 4 together. 10 + (-5) = 5, so we write 5x. -6 and 4 are also = x² + 5x – 2 like terms, so we can combine them to get -2. Isn’t the simplified expression much nicer? Now you try: x² + 5x + 3x² + x³ - 5 + 3 [You should get x³ + 4x² + 5x – 2] Order of Operations PEMDAS – Please Excuse My Dear Aunt Sally, remember that from Algebra class? It tells the order in which we can complete operations when solving an equation.
    [Show full text]
  • 7.2 Binary Operators Closure
    last edited April 19, 2016 7.2 Binary Operators A precise discussion of symmetry benefits from the development of what math- ematicians call a group, which is a special kind of set we have not yet explicitly considered. However, before we define a group and explore its properties, we reconsider several familiar sets and some of their most basic features. Over the last several sections, we have considered many di↵erent kinds of sets. We have considered sets of integers (natural numbers, even numbers, odd numbers), sets of rational numbers, sets of vertices, edges, colors, polyhedra and many others. In many of these examples – though certainly not in all of them – we are familiar with rules that tell us how to combine two elements to form another element. For example, if we are dealing with the natural numbers, we might considered the rules of addition, or the rules of multiplication, both of which tell us how to take two elements of N and combine them to give us a (possibly distinct) third element. This motivates the following definition. Definition 26. Given a set S,abinary operator ? is a rule that takes two elements a, b S and manipulates them to give us a third, not necessarily distinct, element2 a?b. Although the term binary operator might be new to us, we are already familiar with many examples. As hinted to earlier, the rule for adding two numbers to give us a third number is a binary operator on the set of integers, or on the set of rational numbers, or on the set of real numbers.
    [Show full text]
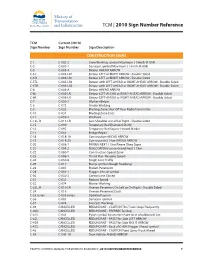
  • 2010 Sign Number Reference for Traffic Control Manual
    TCM | 2010 Sign Number Reference TCM Current (2010) Sign Number Sign Number Sign Description CONSTRUCTION SIGNS C-1 C-002-2 Crew Working symbol Maximum ( ) km/h (R-004) C-2 C-002-1 Surveyor symbol Maximum ( ) km/h (R-004) C-5 C-005-A Detour AHEAD ARROW C-5 L C-005-LR1 Detour LEFT or RIGHT ARROW - Double Sided C-5 R C-005-LR1 Detour LEFT or RIGHT ARROW - Double Sided C-5TL C-005-LR2 Detour with LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-5TR C-005-LR2 Detour with LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-6 C-006-A Detour AHEAD ARROW C-6L C-006-LR Detour LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-6R C-006-LR Detour LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-7 C-050-1 Workers Below C-8 C-072 Grader Working C-9 C-033 Blasting Zone Shut Off Your Radio Transmitter C-10 C-034 Blasting Zone Ends C-11 C-059-2 Washout C-13L, R C-013-LR Low Shoulder on Left or Right - Double Sided C-15 C-090 Temporary Red Diamond SLOW C-16 C-092 Temporary Red Square Hazard Marker C-17 C-051 Bridge Repair C-18 C-018-1A Construction AHEAD ARROW C-19 C-018-2A Construction ( ) km AHEAD ARROW C-20 C-008-1 PAVING NEXT ( ) km Please Obey Signs C-21 C-008-2 SEALCOATING Loose Gravel Next ( ) km C-22 C-080-T Construction Speed Zone C-23 C-086-1 Thank You - Resume Speed C-24 C-030-8 Single Lane Traffic C-25 C-017 Bump symbol (Rough Roadway) C-26 C-007 Broken Pavement C-28 C-001-1 Flagger Ahead symbol C-30 C-030-2 Centre Lane Closed C-31 C-032 Reduce Speed C-32 C-074 Mower Working C-33L, R C-010-LR Uneven Pavement On Left or On Right - Double Sided C-34
    [Show full text]
  • Rules for Matrix Operations
    Math 2270 - Lecture 8: Rules for Matrix Operations Dylan Zwick Fall 2012 This lecture covers section 2.4 of the textbook. 1 Matrix Basix Most of this lecture is about formalizing rules and operations that we’ve already been using in the class up to this point. So, it should be mostly a review, but a necessary one. If any of this is new to you please make sure you understand it, as it is the foundation for everything else we’ll be doing in this course! A matrix is a rectangular array of numbers, and an “m by n” matrix, also written rn x n, has rn rows and n columns. We can add two matrices if they are the same shape and size. Addition is termwise. We can also mul tiply any matrix A by a constant c, and this multiplication just multiplies every entry of A by c. For example: /2 3\ /3 5\ /5 8 (34 )+( 10 Hf \i 2) \\2 3) \\3 5 /1 2\ /3 6 3 3 ‘ = 9 12 1 I 1 2 4) \6 12 1 Moving on. Matrix multiplication is more tricky than matrix addition, because it isn’t done termwise. In fact, if two matrices have the same size and shape, it’s not necessarily true that you can multiply them. In fact, it’s only true if that shape is square. In order to multiply two matrices A and B to get AB the number of columns of A must equal the number of rows of B. So, we could not, for example, multiply a 2 x 3 matrix by a 2 x 3 matrix.
    [Show full text]
  • Operations with Algebraic Expressions: Addition and Subtraction of Monomials
    Operations with Algebraic Expressions: Addition and Subtraction of Monomials A monomial is an algebraic expression that consists of one term. Two or more monomials can be added or subtracted only if they are LIKE TERMS. Like terms are terms that have exactly the SAME variables and exponents on those variables. The coefficients on like terms may be different. Example: 7x2y5 and -2x2y5 These are like terms since both terms have the same variables and the same exponents on those variables. 7x2y5 and -2x3y5 These are NOT like terms since the exponents on x are different. Note: the order that the variables are written in does NOT matter. The different variables and the coefficient in a term are multiplied together and the order of multiplication does NOT matter (For example, 2 x 3 gives the same product as 3 x 2). Example: 8a3bc5 is the same term as 8c5a3b. To prove this, evaluate both terms when a = 2, b = 3 and c = 1. 8a3bc5 = 8(2)3(3)(1)5 = 8(8)(3)(1) = 192 8c5a3b = 8(1)5(2)3(3) = 8(1)(8)(3) = 192 As shown, both terms are equal to 192. To add two or more monomials that are like terms, add the coefficients; keep the variables and exponents on the variables the same. To subtract two or more monomials that are like terms, subtract the coefficients; keep the variables and exponents on the variables the same. Addition and Subtraction of Monomials Example 1: Add 9xy2 and −8xy2 9xy2 + (−8xy2) = [9 + (−8)] xy2 Add the coefficients. Keep the variables and exponents = 1xy2 on the variables the same.
    [Show full text]
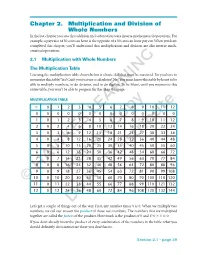
  • Chapter 2. Multiplication and Division of Whole Numbers in the Last Chapter You Saw That Addition and Subtraction Were Inverse Mathematical Operations
    Chapter 2. Multiplication and Division of Whole Numbers In the last chapter you saw that addition and subtraction were inverse mathematical operations. For example, a pay raise of 50 cents an hour is the opposite of a 50 cents an hour pay cut. When you have completed this chapter, you’ll understand that multiplication and division are also inverse math- ematical operations. 2.1 Multiplication with Whole Numbers The Multiplication Table Learning the multiplication table shown below is a basic skill that must be mastered. Do you have to memorize this table? Yes! Can’t you just use a calculator? No! You must know this table by heart to be able to multiply numbers, to do division, and to do algebra. To be blunt, until you memorize this entire table, you won’t be able to progress further than this page. MULTIPLICATION TABLE ϫ 012 345 67 89101112 0 000 000LEARNING 00 000 00 1 012 345 67 89101112 2 024 681012Copy14 16 18 20 22 24 3 036 9121518212427303336 4 0481216 20 24 28 32 36 40 44 48 5051015202530354045505560 6061218243036424854606672Distribute 7071421283542495663707784 8081624324048566472808896 90918273HAWKESReview645546372819099108 10 0 10 20 30 40 50 60 70 80 90 100 110 120 ©11 0 11 22 33 44NOT 55 66 77 88 99 110 121 132 12 0 12 24 36 48 60 72 84 96 108 120 132 144 Do Let’s get a couple of things out of the way. First, any number times 0 is 0. When we multiply two numbers, we call our answer the product of those two numbers.
    [Show full text]
  • Grade 7/8 Math Circles the Scale of Numbers Introduction
    Faculty of Mathematics Centre for Education in Waterloo, Ontario N2L 3G1 Mathematics and Computing Grade 7/8 Math Circles November 21/22/23, 2017 The Scale of Numbers Introduction Last week we quickly took a look at scientific notation, which is one way we can write down really big numbers. We can also use scientific notation to write very small numbers. 1 × 103 = 1; 000 1 × 102 = 100 1 × 101 = 10 1 × 100 = 1 1 × 10−1 = 0:1 1 × 10−2 = 0:01 1 × 10−3 = 0:001 As you can see above, every time the value of the exponent decreases, the number gets smaller by a factor of 10. This pattern continues even into negative exponent values! Another way of picturing negative exponents is as a division by a positive exponent. 1 10−6 = = 0:000001 106 In this lesson we will be looking at some famous, interesting, or important small numbers, and begin slowly working our way up to the biggest numbers ever used in mathematics! Obviously we can come up with any arbitrary number that is either extremely small or extremely large, but the purpose of this lesson is to only look at numbers with some kind of mathematical or scientific significance. 1 Extremely Small Numbers 1. Zero • Zero or `0' is the number that represents nothingness. It is the number with the smallest magnitude. • Zero only began being used as a number around the year 500. Before this, ancient mathematicians struggled with the concept of `nothing' being `something'. 2. Planck's Constant This is the smallest number that we will be looking at today other than zero.
    [Show full text]
  • Glossary of Linear Algebra Terms
    INNER PRODUCT SPACES AND THE GRAM-SCHMIDT PROCESS A. HAVENS 1. The Dot Product and Orthogonality 1.1. Review of the Dot Product. We first recall the notion of the dot product, which gives us a familiar example of an inner product structure on the real vector spaces Rn. This product is connected to the Euclidean geometry of Rn, via lengths and angles measured in Rn. Later, we will introduce inner product spaces in general, and use their structure to define general notions of length and angle on other vector spaces. Definition 1.1. The dot product of real n-vectors in the Euclidean vector space Rn is the scalar product · : Rn × Rn ! R given by the rule n n ! n X X X (u; v) = uiei; viei 7! uivi : i=1 i=1 i n Here BS := (e1;:::; en) is the standard basis of R . With respect to our conventions on basis and matrix multiplication, we may also express the dot product as the matrix-vector product 2 3 v1 6 7 t î ó 6 . 7 u v = u1 : : : un 6 . 7 : 4 5 vn It is a good exercise to verify the following proposition. Proposition 1.1. Let u; v; w 2 Rn be any real n-vectors, and s; t 2 R be any scalars. The Euclidean dot product (u; v) 7! u · v satisfies the following properties. (i:) The dot product is symmetric: u · v = v · u. (ii:) The dot product is bilinear: • (su) · v = s(u · v) = u · (sv), • (u + v) · w = u · w + v · w.
    [Show full text]