Session 20 Astrophysics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Additional Karaoke Listings Updated February 2021! 1
Artist Song Title 1975 Chocolate 1975, The Sincerity is Scary 5 Seconds of Summer Want you back 5 Seconds of Summer Easier ACDC Big Balls Adele All I Ask Adele Cold Shoulder Adele Melt My Heart to Stone Adele Million Years Ago Adele Sweetest Devotion Adele Hello Adele I Can't Make You Love Me Adele Love in The Dark Adele One and Only Adele Send My Love to Your New Lover Adele Take It All Adele When We Were Young Adele Remedy Adele Love Song Afroman Colt 45 AJR Burn the House Down Alabama Angels Among us Alabama Forty Hour Week Alabama Roll on Eighteen Wheeler Alabama Lady down on love Alaina, Lauren Road Less Traveled Alaina, Lauren Wings of an Angel Alaina, Lauren Ladies in the 90s Alaina, Lauren Getting Good Alaina, Lauren Other Side, The Aldean, Jason Tattoos on this town ADDITIONAL KARAOKE LISTINGS UPDATED FEBRUARY 2021! 1 Aldean, Jason Just Getting Started Aldean, Jason Lights Come On Aldean, Jason Little More Summertime, A Aldean, Jason This Plane Don't Go There Aldean, Jason Tonight Looks Good On You Aldean, Jason Gettin Warmed up Aldean, Jason Truth, The Aldean, Jason You make it easy Aldean, Jason Girl Like you Aldean, Jason Camouflage Hat Aldean, Jason We Back Aldean, Jason Rearview Town Aldean, Jason & Miranda Lambert Drowns The Whiskey Alice in Chains Man In The Box Alice in Chains No Excuses Alice in Chains Your Decision Alice in Chains Nutshell Alice in Chains Rooster Allan, Gary Every Storm (Runs Out of Rain) Allan, Gary Runaway Allen, Jimmie Best shot Anderson, John Swingin' Andress, Ingrid Lady Like Andress, Ingrid More Hearts Than Mine Angels and Airwaves Kiss & Tell Angston, Jon When it comes to loving you Animals, The Bring It On Home To Me Arctic Monkeys Do I Wanna Know Ariana Grande Breathin Arthur, James Say You Won't Let Go Arthur, James Naked Arthur, James Empty Space ADDITIONAL KARAOKE LISTINGS UPDATED FEBRUARY 2021! 2 Arthur, James Falling like the stars Arthur, James & Anne Marie Rewrite the Stars Arthur, James & Anne Marie Rewrite The Stars Ashanti Happy Ashanti Helpless (ft. -

Bell & Company Complete Song List
Bell & Company Complete Song List A-Ha Take On Me AC/DC It's A Long Way To The Top Highway to Hell Andy Grammer Honey I'm Good Avicii Wake Me Up Backstreet Boys I Want It That Way Beatles, The Across The Universe All You Need Is Love Blackbird Girl Here Comes The Sun Hey Jude I’ve Just Seen A Face In My Life Norwegian Wood Ob La Di Ob La Da Oh! Darling Please Please Me Twist and Shout Two of Us We Can Work It Out When I’m Sixty-Four With A Little Help From My Friends Yellow Submarine Beck Loser Bee Gees, The Stayin' Alive Ben E. King Stand By Me Ben Harper Steal My Kisses Bill Conti Gonna Fly Now (Theme From Rocky) Bill Withers Ain't No Sunshine Lovely Day Billy Idol Dancing With Myself Rebel Yell Billy Joel Only The Good Die Young Piano Man You May Be Right Black Eyed Peas I Got A Feeling Blink 182 All The Small Things Bloodhound Gang The Bad Touch Blur Girls And Boys Bob Dylan Don't Think Twice Knockin’ On Heavens Door Shelter From The Storm Tangled Up In Blue Bob Marley Is This Love Bon Jovi Dead Or Alive Boz Scaggs Lido Shuffle Britney Spears Toxic Brooks And Dunn Boot Scootin' Boogie Bruce Springsteen Blinded By The Light I’m On Fire Bruno Mars The Lazy Song Uptown Bryan Adams Summer Of '69 Buddy Holly Everyday Not Fade Away Capital Cities Safe And Sound Cat Stevens Father And Son If You Want To Sing Out Into White The Wind CeeLo Green Forget You Cheap Trick I Want You To Want Me Chris Isaak Wicked Game Christina Perri A Thousand Years Christopher Cross Ride Like The Wind Chuck Berry Johnny B. -

Satisfaction Rolling Stones 1965 3 American Pie Don Mclean 1972 4
AS VOTED AT OLDIESBOARD.COM 10/30/17 THROUGH 12/4/17 CONGRATULATIONS TO “HEY JUDE”, THE #1 SELECTION FOR THE 19 TH TIME IN 20 YEARS! Ti tle Artist Year 1 Hey Jude Beatles 1968 2 (I Can’t Get No) Satisfaction Rolling Stones 1965 3 American Pie Don McLean 1972 4 Light My Fire Doors 1967 5 In The Still Of The Nite Five Satins 1956 6 I Want To Hold Your Hand Beatles 1964 7 MacArthur Park Richard Harris 1968 8 Rag Doll Four Seasons 1964 9 God Only Knows Beach Boys 1966 10 Ain't No Mount ain High Enough Diana Ross 1970 11 Bridge Over Troubled Water Simon and Garfunkel 1970 12 Because Dave Clark Five 1964 13 Good Vibrations Beach Boys 1966 14 Cherish Association 1966 15 She Loves You Beatles 1964 16 Hotel California Eagles 1977 17 St airway To Heaven Led Zeppelin 1971 18 Born To Run Bruce Springsteen 1975 19 My Girl Temptations 1965 20 Let It Be Beatles 1970 21 Be My Baby Ronettes 1963 22 Downtown Petula Clark 1965 23 Since I Don't Have You Skyliners 1959 24 To Sir With Love Lul u 1967 25 Brandy (You're A Fine Girl) Looking Glass 1972 26 Suspicious Minds Elvis Presley 1969 27 You've Lost That Lovin' Feelin' Righteous Brothers 1965 28 You Really Got Me Kinks 19 64 29 Wichita Lineman Glen Campbell 1968 30 The Rain The Park & Ot her Things Cowsills 1967 31 A Hard Day's Night Beatles 1964 32 A Day In The Life Beatles 1967 33 Rock Around The Clock Bill Haley & His Comets 1955 34 Imagine John Lennon 1971 35 I Only Have Eyes For You Flamingos 1959 36 Waterloo Sunset Kinks 1967 37 Bohemian Rhapsody Queen 76 -92 38 Sugar Sugar Archies 1969 39 What's -

Horizon's Door
Bard College Bard Digital Commons Senior Projects Spring 2018 Bard Undergraduate Senior Projects Spring 2018 Horizon's Door Mackenzie Kristofco Bard College, [email protected] Follow this and additional works at: https://digitalcommons.bard.edu/senproj_s2018 Part of the Poetry Commons This work is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 4.0 License. Recommended Citation Kristofco, Mackenzie, "Horizon's Door" (2018). Senior Projects Spring 2018. 338. https://digitalcommons.bard.edu/senproj_s2018/338 This Open Access work is protected by copyright and/or related rights. It has been provided to you by Bard College's Stevenson Library with permission from the rights-holder(s). You are free to use this work in any way that is permitted by the copyright and related rights. For other uses you need to obtain permission from the rights- holder(s) directly, unless additional rights are indicated by a Creative Commons license in the record and/or on the work itself. For more information, please contact [email protected]. Horizon’s Door Senior Project Submitted to The Division of Language and Literature of Bard College By Mackenzie James Kristofco Annandale-on-Hudson, NY May 2018 Acknowledgements for my family, without whom I would never understand the necessity of care for my dear friends, whose compassion, support, humor and strangeness lift my steps each day for Robert, who continually shows me that I know how to listen to the world who continually shows me what any of us mean by poetry for Katie, who turned on the light 1 Contents I. The Approaching Vista 6 Poem For Beginning 7 Thalassocracy 8 Recalling The Conversation 9 After Sze Tsung Leong’s Photograph of Cairo 10 Secret Places 11 Remembrance Of The Island 12 Warmth 13 Between Breaths 14 Back Breathes The Ocean 15 Moon’s Language 16 In The Morning 17 II. -
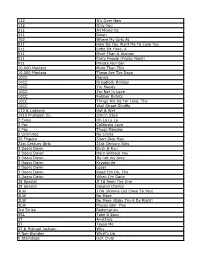
112 It's Over Now 112 Only You 311 All Mixed up 311 Down
112 It's Over Now 112 Only You 311 All Mixed Up 311 Down 702 Where My Girls At 911 How Do You Want Me To Love You 911 Little Bit More, A 911 More Than A Woman 911 Party People (Friday Night) 911 Private Number 10,000 Maniacs More Than This 10,000 Maniacs These Are The Days 10CC Donna 10CC Dreadlock Holiday 10CC I'm Mandy 10CC I'm Not In Love 10CC Rubber Bullets 10CC Things We Do For Love, The 10CC Wall Street Shuffle 112 & Ludacris Hot & Wet 1910 Fruitgum Co. Simon Says 2 Evisa Oh La La La 2 Pac California Love 2 Pac Thugz Mansion 2 Unlimited No Limits 20 Fingers Short Dick Man 21st Century Girls 21st Century Girls 3 Doors Down Duck & Run 3 Doors Down Here Without You 3 Doors Down Its not my time 3 Doors Down Kryptonite 3 Doors Down Loser 3 Doors Down Road I'm On, The 3 Doors Down When I'm Gone 38 Special If I'd Been The One 38 Special Second Chance 3LW I Do (Wanna Get Close To You) 3LW No More 3LW No More (Baby I'm A Do Right) 3LW Playas Gon' Play 3rd Strike Redemption 3SL Take It Easy 3T Anything 3T Tease Me 3T & Michael Jackson Why 4 Non Blondes What's Up 5 Stairsteps Ooh Child 50 Cent Disco Inferno 50 Cent If I Can't 50 Cent In Da Club 50 Cent In Da Club 50 Cent P.I.M.P. (Radio Version) 50 Cent Wanksta 50 Cent & Eminem Patiently Waiting 50 Cent & Nate Dogg 21 Questions 5th Dimension Aquarius_Let the sunshine inB 5th Dimension One less Bell to answer 5th Dimension Stoned Soul Picnic 5th Dimension Up Up & Away 5th Dimension Wedding Blue Bells 5th Dimension, The Last Night I Didn't Get To Sleep At All 69 Boys Tootsie Roll 8 Stops 7 Question -
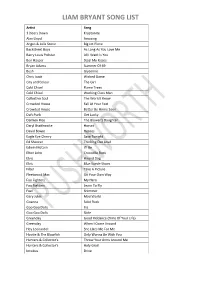
Liam Bryant Song List
LIAM BRYANT SONG LIST Artist Song 3 Doors Down Kryptonite Alex Lloyd Amazing Angus & Julia Stone Big Jet Plane Backstreet Boys As Long As You Love Me Barry Louis Polistar All I Want Is You Ben Harper Steal My Kisses Bryan Adams Summer Of 69 Bush Glycerine Chris Isaak Wicked Game City and Colour The Girl Cold Chisel Flame Trees Cold Chisel Working Class Man Collective Soul The World I Know Crowded House Fall At Your Feet Crowded House Better Be Home Soon Daft Punk Get Lucky Damien Rice The Blower's Daughter Daryl Braithwaite Horses David Bowie Heroes Eagle Eye Cherry Save Tonight Ed Sheeran Thinking Out Loud Edwin McCain I'll Be Elton John Crocodile Rock Elvis Hound Dog Elvis Blue Suede Shoes Filter Take A Picture Fleetwood Mac Go Your Own Way Foo Fighters My Hero Foo Fighters Learn To Fly Fuel Shimmer Gary Jules Mad World Goanna Solid Rock Goo Goo Dolls Iris Goo Goo Dolls Slide Greenday Good Riddance (Time Of Your Life) Greenday When I Come Around Hey Leonardo! She Likes Me For Me Hootie & The Blowfish Only Wanna Be With You Hunters & Collector's Throw Your Arms Around Me Hunters & Collector's Holy Grail Incubus Drive LIAM BRYANT SONG LIST Inner Circle Sweat Jack Johnson Flake Jack Johnson Sitting, Waiting, Wishing Jeff Buckley Halleluiah Jennifer Paige Crush Jimmy Buffett Escape Pina Colada John Legend All Of Me John Lennon Imagine Johnny Cash Ring of Fire Jose Gonzalez Heartbeats Kenny Rogers The Gambler Kings Of Leon Use Somebody Lauryn Hill Can't Take My Eyes Off You Lenny Kravitz Again Leonardo's Bride Even When I'm Sleeping Lifehouse -

Pink Floyd - Dark Side of the Moon Speak to Me Breathe on the Run Time the Great Gig in the Sky Money Us and Them Any Colour You Like Brain Damage Eclipse
Pink Floyd - Dark Side of the Moon Speak to Me Breathe On the Run Time The Great Gig in the Sky Money Us and Them Any Colour You Like Brain Damage Eclipse Pink Floyd – The Wall In the Flesh The Thin Ice Another Brick in the Wall (Part 1) The Happiest Days of our Lives Another Brick in the Wall (Part 2) Mother Goodbye Blue Sky Empty Spaces Young Lust Another Brick in the Wall (Part 3) Hey You Comfortably Numb Stop The Trial Run Like Hell Laser Queen Bicycle Race Don't Stop Me Now Another One Bites The Dust I Want To Break Free Under Pressure Killer Queen Bohemian Rhapsody Radio Gaga Princes Of The Universe The Show Must Go On 1 Laser Rush 2112 I. Overture II. The Temples of Syrinx III. Discovery IV. Presentation V. Oracle: The Dream VI. Soliloquy VII. Grand Finale A Passage to Bangkok The Twilight Zone Lessons Tears Something for Nothing Laser Radiohead Airbag The Bends You – DG High and Dry Packt like Sardine in a Crushd Tin Box Pyramid song Karma Police The National Anthem Paranoid Android Idioteque Laser Genesis Turn It On Again Invisible Touch Sledgehammer Tonight, Tonight, Tonight Land Of Confusion Mama Sussudio Follow You, Follow Me In The Air Tonight Abacab 2 Laser Zeppelin Song Remains the Same Over the Hills, and Far Away Good Times, Bad Times Immigrant Song No Quarter Black Dog Livin’, Lovin’ Maid Kashmir Stairway to Heaven Whole Lotta Love Rock - n - Roll Laser Green Day Welcome to Paradise She Longview Good Riddance Brainstew Jaded Minority Holiday BLVD of Broken Dreams American Idiot Laser U2 Where the Streets Have No Name I Will Follow Beautiful Day Sunday, Bloody Sunday October The Fly Mysterious Ways Pride (In the Name of Love) Zoo Station With or Without You Desire New Year’s Day 3 Laser Metallica For Whom the Bell Tolls Ain’t My Bitch One Fuel Nothing Else Matters Master of Puppets Unforgiven II Sad But True Enter Sandman Laser Beatles Magical Mystery Tour I Wanna Hold Your Hand Twist and Shout A Hard Day’s Night Nowhere Man Help! Yesterday Octopus’ Garden Revolution Sgt. -

C a L L a N S E T L I
C A L L A N S E T L I S T Aloe Blacc - I Need A Dollar Alt-J - Breezeblocks Angus & Julia Stone - Big Jet Plane Angus & Julia Stone - Wedding Song Birds Of Tokyo - Lanterns Birds Of Tokyo - Plans Bon Iver -Skinny Love Chris Isaak - Wicked Game Christina Perri - Thousand Years Coldplay - Clocks Coldplay - Don’t Panic Coldplay - God Put A Smile Upon Your Face Coldplay - Scientist Coldplay - Viva La Vida Crowded House - Don’t Dream Its Over Crowded House - Fall At Your Feet Damien Rice - The Blowers Daughter Dean Lewis - Waves Disclosure - Latch Drake - Hotline Bling Ed Sheeran - Castle On The Hill Ed Sheeran - Shape Of You Ed Sheeran - Thinking Out Loud Elvis - Can't Help Falling In Love Gary Jewels - Mad World Gotye - Hearts A Mess James Bay - Let It Go Jamie Lawson - I Wasn't Expecting That John Legend - All Of Me José González - Heart Beats Julia Jacklin - Pool Party Keane - Somewhere Only We Know Kimbra - Settle Down Kyle Lionhart - Slow Sips Maroon 5 - Sunday Morning Matt Corby - Resolution Nick Cave & The Bad Seeds - Into My Arms Paramore - Only Exception Pearl Jam - Breathe Radiohead - Paranoid Android Red Hot Chili Peppers - Zephyr Zong Snow Patrol - Chasing Cars Sticky Fingers - Gold Snafu Tamia - So Into You Tears For Fears - Everybody Wants To Rule The World The Church - Under The Milky Way The Fray - How To Save A Life The Paper Kites - Bloom The Reubens - Elvis The Reubens - Paddy The Subways - Strawberry Blonde The Wombats - Turn The Xx - Angels Youth Group - Forever Young -

Jonny Maldonado Song List
JONNY MALDONADO SONG LIST A Day in the Life: The Beatles Across the Universe: The Beatles Ain’t No Sunshine: Bill Withers All Along the Watchtower: Bob Dylan All the Way: Frank Sinatra And I Love Her: The Beatles And I Love You So: Don McLean Another Brick in the Wall: Pink Floyd Autumn Leaves: Nat King Cole Baby Come Back: Player Baby I Love Your Way: Peter Frampton Besame Mucho: Spanish Classic Best of My Love: The Eagles Big Yellow Taxi: Joni Mitchell Billy Jean: Michael Jackson Black and Gold: Sam Sparro Black Hole Sun: Chris Cornell Black Velvet: Alannah Myles Black: Pearl Jam Brandy: Looking Glass Bridge Over Troubled Water: Simon and Garfunkel California Dreaming: The Mamas and the Papas Can’t Help Falling in Love: Elvis Presley Can’t Make You Love Me: Bonnie Raitt Cannonball: Damien Rice Careless Whispers: George Michaels Carolina on My Mind: James Taylor Cats in the Cradle: Harry Chapin Change the World: Eric Clapton Chasing Cars: Snow Patrol Chim Chimney: Mary Poppins Close to You: The Carpenters Come as You Are: Nirvana Come Out Tonight: Jeffrey Gaines Come Together: The Beatles Constant Craving: kd Lang Cool Change: Little River Band Corcovado: Brazilian Classic Country Road: John Denver Crazy Little Thing Called Love: Queen Crazy Love: Van Morrison Cream: Prince Creep: Radiohead Cuts Like a Knife: Bryan Adams Dance Me Till the End of Love: Leonard Cohen Daniel: Elton John Danny’s Song: Kenny Loggins Delicate: Damien Rice Do it Again: Steely Dan Don’t Change a Thing: INXS Don’t Dream it’s Over: Crowded House Don’t Know Why: -

Music Inspired by Astronomy, Organized by Topic an Annotated Listing by Andrew Fraknoi
Music Inspired by Astronomy, Organized by Topic An Annotated Listing by Andrew Fraknoi © copyright 2019 by Andrew Fraknoi. All rights reserved. Used with permission. Borresen: At Uranienborg Cage: Atlas Eclipticalis Glass: Orion Connections between astronomy and music have been proposed since the time of the ancient Greeks. This annotated listing of both classical and popular music inspired by astronomy restricts itself to music that has connections to real science -- not just an astronomical term or two in the title or lyrics. For example, we do not list Gustav Holst’s popular symphonic suite The Planets, because it draws its inspiration from the astrological, and not astronomical, characteristics of the worlds in the solar system. Similarly, songs like Soundgarden’s “Black Hole Sun” or the Beatles’ “Across the Universe” just don’t contain enough serious astronomy to make it into our guide. When possible, we give links to a CD and a YouTube recording or explanation for each piece. The music is arranged in categories by astronomical topic, from asteroids to Venus. Additions to this list are most welcome (as long as they follow the above guidelines); please send them to the author at: fraknoi {at} fhda {dot} edu Table of Contents Asteroids Meteors and Meteorites Astronomers Moon Astronomy in General Nebulae Black Holes Physics Related to Astronomy Calendar, Time, Seasons Planets (in General) Comets Pluto Constellations Saturn Cosmology SETI (Search for Intelligent Life Out There) Earth Sky Phenomena Eclipses Space Travel Einstein Star Clusters Exoplanets Stars and Stellar Evolution Galaxies and Quasars Sun History of Astronomy Telescopes and Observatories Jupiter Venus Mars 1 Asteroids Coates, Gloria Among the Asteroids on At Midnight (on Tzadik). -

Acoustic Avenue Duo/Trio Song List
ACOUSTIC AVENUE DUO/TRIO SONG LIST This list does not include all songs performed Aint Seen Nothin Yet Bachman Turner Leaving On a Jet Plane Bob Dylan Across The Universe The Beatles Mr Jones Counting Crows Ain’t No Sunshine Bill Withers My Happiness Powderfinger All I Have To Do The Everly Brothers Mrs. Robinson Simon and Garfunkle Amazing Alex Lloyd Open Your Eyes Snow Patrol Another Lonely Day Ben Harper Only Wanna be with you Hootie and The Blowfish April Sun Dragon Peaches and Cream John Butler Trio Better Be Home Soon Crowded House Purple Sneakers You Am I Better Man Pearl Jam Put Your Records On Corinne Bailey Rae Breakfast at Tiffanys Deep Blue Something Passenger Powderfinger Boys Light Up Australian Crawl Pictures Sneaky Sound System Baby I Love Your Way Pater Frampton Run To Paradise The Choirboys Bad Moon Rising CCR Steal My Kisses Ben Harper Brown Eyed Girl Van Morrison Summer Of 69 Bryan Adams Black Finger Nails Eskimo Joe Save Tonight Eagle Eye Cherry Clocks Coldplay Somebody Told Me The Killers Cherry Bomb John Mellencamp Stuck In The Middle Steelers Wheel Dumb Things Paul Kelly Strong Enough Sheryl Crow Drugs Don’t Work The Verve Sitting On The Dock Otis Redding Down Hearted Australian Crawl Suddenly I see KT Tunstall Don’t Dream Its Over Crowded House Something So Strong Crowded House Dreams Fleetwood Mac Shot Through The Heart Bon Jovi Daydream Believer The Monkeys Take It Easy The Eagles Don’t Look Back Oasis 20 Good Reasons Thirsty Merc Don’t Stop Fleetwood Mac Throw Your Arms Hunters and Collectors Down On The Corner -

Rachel Laing Song List - Updated 28 02 2019
RACHEL LAING SONG LIST - UPDATED 28 02 2019 SONG TITLE ORIGINAL ARTIST VERSION (IF NOT ORIGINAL) 3AM MATCHBOX 20 100 YEARS FIVE FOR FIGHTING 500 MILES (I'M GONNA BE) THE PROCLAIMERS 93 MILLION MILES JASON MRAZ A HORSE WITH NO NAME AMERICA A THOUSAND MILES VANESSA CARLTON A THOUSAND YEARS CHRISTINA PERRI A WHITE SPORTS COAT MARTY ROBBINS ABOVE GROUND NORAH JONES ADORN MIGUEL ADVANCE AUSTRALIA FAIR NATIONAL ANTHEM AHEAD OF MYSELF JAMIE LAWSON AINT NO SUNSHINE BILL WITHERS ALIVE SIA ALL ABOUT THAT BASS MEGHAN TRAINOR ALL OF ME JOHN LEGEND ALL THE SMALL THINGS BLINK 182 ALL TIME LOW JOHN BELLION ANDY GRAMMER ALWAYS ON MY MIND ELVIS AM I EVER GONNA SEE YOUR FACE AGAIN THE ANGELS RACHEL LAING AM I NOT PRETTY ENOUGH KASEY CHAMBERS AM I WRONG NICO & VINZ AMAZING GRACE AND THE BOYS ANGUS & JULIA STONE ANGEL SARAH MCLAUGHLAN ANGELS ROBBIE WILLIAMS ANNIES SONG JOHN DENVER ANOTHER DAY IN PARADISE PHIL COLLINS APOLOGIZE ONE REPUBLIC APRIL SUN IN CUBA DRAGON ARE YOU GONNA BE MY GIRL JET ARE YOU OLD ENOUGH DRAGON ARMY OF TWO OLLY MURS AT LAST ETTA JAMES AULD LANG SYNE AUTUMN LEAVES NAT KING COLE EVA CASSIDY BABY CAN I HOLD YOU TRACEY CHAPMAN BACK TO DECEMBER TAYLOR SWIFT BAD MOON RISING CREEDENCE CLEARWATER REVIVAL BAIL ME OUT PETE MURRAY BASKET CASE SARA BARELLIS BE HERE TO LOVE ME NORAH JONES BE MY SOMEBODY NORAH JONES BEAUTIFUL IN MY EYES JOSHUA KADISON BESEME MUCHO BEST FRIENDS BRANDY BETTE DAVIS EYES KIM CARNES BETTER BE HOME SOON CROWDED HOUSE BETTER MAN PEARL JAM BETTER THAN JOHN BUTLER TRIO BIG DEAL LEANNE RIMES BIG JET PLANE ANGUS & JULIA STONE