DOCSLIB.ORG

Nureg/Cr-7206 Pnnl-23701

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Nureg/Cr-7206 Pnnl-23701 NUREG/CR-7206 PNNL-23701 Spent Fuel Transportation Package Response to the MacArthur Maze Fire Scenario Final Report Office of Nuclear Material Safety and Safeguards NUREG/CR-7206 PNNL-23701 Spent Fuel Transportation Package Response to the MacArthur Maze Fire Scenario Final Report Manuscript Completed: July 2016 Date Published: October 2016 Prepared by: H. E. Adkins, Jr.1, J. M. Cuta1, N. A. Klymyshyn1, S. R. Suffield1, C. S. Bajwa2, K. B. McGrattan3, C. E. Beyer1, and A. Sotomayor-Rivera4 1Pacific Northwest National Laboratory P. O. Box 999 Richland, WA 99352 2International Atomic Energy Agency Vienna International Centre P.O. Box 100 A-1400 Vienna, Austria 3National Institute of Standards and Technology Engineering Laboratory 100 Bureau Drive, Stop 8600 Gaithersburg, MD 20899-8600 4U.S. Nuclear Regulatory Commission J. Piotter, NRC Project Manager NRC Job Code J5710 Office of Nuclear Material Safety and Safeguards ABSTRACT The U.S. Nuclear Regulatory Commission has established requirements for packaging and transportation of spent nuclear fuel assemblies under normal conditions of transport and for hypothetical accident conditions. Real-world accidents of greater severity are possible, but are of much lower probability, and the probability of such an accident involving a spent nuclear fuel (SNF) package is even lower. However, because of the potential consequences, the U.S. Nuclear Regulatory Commission has undertaken the examination of specific accidents to determine the potential consequences to an SNF package. The MacArthur Maze accident of April 2007, which did not involve SNF, was selected for evaluation because of the severity of the fire and the unusual structural consequences, in which the heat from the fire caused the overhead roadway segments to collapse onto the roadway where the fire was burning. The General Atomics GA-4 legal weight truck transportation package was selected for this investigation. Based on fire modeling with the Fire Dynamics Simulator code, and physical examination of material samples obtained onsite, a bounding fire scenario was defined for this accident. The complex and dynamic fire conditions are represented as a fully engulfing pool fire at 2012°F (1100°C) prior to the overhead roadway collapse, and as a smaller and less severe fully engulfing pool fire at 1652°F (900°C) afterward. Thermal models of the GA-4 package were constructed for the ANSYS and COBRA-SFS codes, to determine the response of the package to the fire scenario, including the long post-fire cooldown transient. Additional detailed structural and thermal-structural models were developed using ANSYS and LS-DYNA for the roadway and package, which showed that the falling overhead segments could impose only relatively innocuous loads on the stainless steel body and DU gamma shield, compared to the hypothetical accident conditions structural loading that the package is designed to withstand. Thermal evaluations of the package response to this fire scenario predict that the peak cladding temperature would exceed the short-term limit of 1058°F (570°C) long before the end of the fire. Maximum cladding temperatures on all rods in the package are predicted to exceed this temperature limit in the course of the transient, and remain above this limit for several hours. The maximum peak cladding temperature in the transient is predicted to be in the range of 1350-1400°F (732-760°C), and occurs approximately 3 hours after the end of the postulated fire accident. Temperatures in the regions of the package seals exceed the seal material limits for most of the fire duration. The FRAPTRAN-1.4 code was used to estimate a fuel rod burst rupture temperature of 1097°F (592°C). Together with the temperature histories of the fuel, this suggests that there is the potential for all rods in the package to rupture in this fire scenario. The package seals are assumed to fail. However, a detailed thermo-structural model showed that the lid closure bolts maintain a positive clamping force throughout the transient, thus limiting the release. Using conservative and bounding modeling assumptions, the total possible release was estimated at approximately one-fourth of the mixture A2. Since the regulatory limit is specified as an A2 quantity per week for accident conditions, the estimated release is below the prescribed limit for safety. Therefore this very conservative estimate indicates that the potential release from this package, were it to be involved in a fire accident as severe as the MacArthur Maze fire scenario, would not pose a risk to public health and safety. iii TABLE OF CONTENTS ABSTRACT ................................................................................................................... iii LIST OF FIGURES........................................................................................................ vii LIST OF TABLES .......................................................................................................... xi EXECUTIVE SUMMARY ............................................................................................. xiii ACKNOWLEDGMENTS ............................................................................................. xxv ABBREVIATIONS AND ACRONYMS ...................................................................... xxvii 1.0 INTRODUCTION .................................................................................................. 1-1 2.0 THE MACARTHUR MAZE FIRE ......................................................................... 2-1 2.1 Description of the MacArthur Maze Fire ................................................................. 2-1 2.2 Maximum Material Temperatures in the MacArthur Maze Fire ............................... 2-7 3.0 NUMERICAL MODELING OF THE MACARTHUR MAZE FIRE ......................... 3-1 3.1 FDS Model Geometry ............................................................................................ 3-1 3.2 FDS Model Fire ..................................................................................................... 3-3 3.3 FDS Fire Model Output .......................................................................................... 3-5 3.4 Fire Model Results for Pre-Collapse Configuration ................................................ 3-9 3.5 Bounding Assumptions for Post-Collapse Fire ..................................................... 3-10 4.0 THE MACARTHUR MAZE FIRE SCENARIO...................................................... 4-1 4.1 Thermal Conditions in MacArthur Maze Fire Scenario ........................................... 4-1 4.2 Structural Loads in MacArthur Maze Fire Scenario ................................................ 4-2 5.0 ANALYTICAL MODELS FOR THE MACARTHUR MAZE FIRE SCENARIO ..... 5-1 5.1 GA-4 Legal Weight Truck Spent Fuel Shipping Package ....................................... 5-1 5.2 ANSYS Model of GA-4 Package ............................................................................ 5-3 5.2.1 GA-4 Package Representation .................................................................. 5-3 5.2.2 GA-4 Package beneath Collapsed Roadway ............................................ 5-9 5.2.3 Material Properties for GA-4 Package in ANSYS Model .......................... 5-15 5.3 COBRA-SFS Model of GA-4 Package ................................................................. 5-17 5.3.1 COBRA-SFS Model of GA-4 Package in Fully Engulfing Pool Fire .......... 5-18 5.3.2 COBRA-SFS Model of GA-4 Package beneath Collapsed Upper Roadway ................................................................................................. 5-19 5.4 Structural Models for the MacArthur Maze Fire Scenario ..................................... 5-20 5.4.1 Structural Models for Roadway Drop Scenarios ...................................... 5-20 5.4.2 Preliminary Models for GA-4 Bolt Thermal Expansion Calculations ......... 5-27 5.4.3 Detailed Models for GA-4 Closure Lid Bolt Evaluations ........................... 5-31 6.0 ANALYSIS METHOD .......................................................................................... 6-1 6.1 NCT and HAC Fire for GA-4 Package .................................................................... 6-1 6.2 Thermal Modeling Assumptions ............................................................................. 6-2 6.3 Thermal Boundary Conditions for GA-4 Package Models ...................................... 6-4 6.3.1 Thermal Boundary Conditions ................................................................... 6-5 6.4 Structural Impact Model Assumptions and Analysis Method .................................. 6-8 6.4.1 Overpass Temperature Evaluation .......................................................... 6-10 v 7.0 ANALYSIS RESULTS ......................................................................................... 7-1 7.1 GA-4 Package: Thermal Results for Fire Transient ................................................ 7-1 7.1.1 Pre-collapse Fire (2012°F [1100°C]) ......................................................... 7-2 7.1.2 Post-collapse Fire (1352°F [900°C]) .......................................................... 7-5 7.2 GA-4 Package: Thermal Results for Post-Fire Cooldown Transient ....................... 7-9 7.3 GA-4 Package: Structural Evaluation ................................................................... 7-15 7.3.1 Structural Case #1: Package Perpendicular to Upper Roadway Girders ...................................................................................................
Load more

Recommended publications
  • Please Refrain from Wearing Scented Products (Perfume, Cologne
    SAN FRANCISCO BAY AREA RAPID TRANSIT DISTRICT 300 Lakeside Drive, P. O. Box 12688, Oakland, CA 94604-2688 NOTICE OF MEETING AND AGENDA BOND OVERSIGHT COMMITTEE Wednesday, July 26, 2017 4:00 p.m. – 6:00 p.m. COMMITTEE MEMBERS: Marian Breitbart, Michael Day, Daren Gee, Christine D. Johnson, Michael McGill, Anu Natarajan, John Post Meeting of the Bond Oversight Committee on Wednesday, July 26, 2017, at 4:00 p.m. The Meeting will be held in the 1800 Conference Room, 300 Lakeside Dr., 18th Floor, Oakland, California. AGENDA 1. CALL TO ORDER A. Roll Call. 2. INTRODUCTION OF COMMITTEE MEMBERS 3. INTRODUCTION OF BART STAFF 4. COMMITTEE ROLE A. Controller-Treasurer’s Office is official point of contact for all matters B. Audio recording of meetings C. Meeting Agendas/Minutes D. Annual Report writing and approval process E. Request for photos and bio for website F. Clipper Card/Travel reimbursement G. Introduce process of selecting Committee Chair and Vice Chair 5. PRESENTATION: MEASURE RR OVERALL PROGRAM 6. PRESENTATION: STATUS OF BONDS SOLD 7. Q&A WITH STAFF 8. STAFF REQUEST TO PRESENT ASSET MANAGEMENT AT NEXT MEETING 9. SETTING NEXT MEETING DATE AND AGENDA 10. PUBLIC COMMENT Please refrain from wearing scented products (perfume, cologne, after-shave, etc.) to this meeting, as there may be people in attendance susceptible to environmental illnesses. BART provides services/accommodations upon request to persons with disabilities and individuals who are limited English proficient who wish to address BART Board matters. A request must be made within one and five days in advance of a Board or committee meeting, depending on the service requested.
    [Show full text]
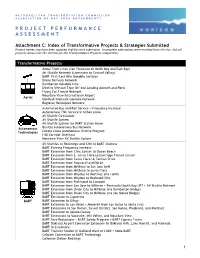
  • Attachment C: Index of Transformative Projects & Strategies Submitted Project Names May Have Been Updated Slightly Since Submission
    METROPOLITAN TRANSPORTATION COMMISSION ASSOCIATION OF BAY AREA GOVERNMENTS PROJECT PERFORMANCE ASSESSMENT Attachment C: Index of Transformative Projects & Strategies Submitted Project names may have been updated slightly since submission. Incomplete submissions were omitted from this list. Not all projects shown met the criteria for the Transformative Projects competition. Transformative Projects Aerial Tram Lines (San Francisco to North Bay and East Bay) Air Shuttle Network (Livermore to Central Valley) BART First/Last Mile Gondola Services Drone Delivery Network Dumbarton Gondola Line Electric Vertical Take Off and Landing Aircraft and Ports Flying Car Transit Network Mountain View International Airport Aerial Oakland/Alameda Gondola Network Regional Helicopter Network Automated Bus and Rail Service + Frequency Increase Autonomous TNC Service in Urban Areas AV Shuttle Circulators AV Shuttle System AV Shuttle System for BART Station Areas Autonomous Benicia Autonomous Bus Network Technologies Contra Costa Autonomous Shuttle Program I-80 Corridor Overhaul Mountain View AV Shuttle System AV Shuttles at Rockridge and 12th St BART Stations BART Evening Frequency Increase BART Extension from Civic Center to Ocean Beach BART Extension from E. Santa Clara to Eastridge Transit Center BART Extension from Santa Clara to Tasman Drive BART Extension from Hayward to Millbrae BART Extension from Millbrae to San Jose (x4) BART Extension from Millbrae to Santa Clara BART Extension from Milpitas to Martinez (via I-680) BART Extension from Milpitas to
    [Show full text]
  • Map of All Transbay Bus Lines
    ORINDA CITY COUNTRY OFFICES ORINDA OrindaWY. BART PABLO CLUB PO FOOTHILL SQUARE CASTRO VALLEY BART ORINDA ROCKRIDGE BART OAKLAND AIRPORT CAMINO ASHBY BART PINOLE RD. VALLEY Upper San Leandro HAYWARD BART Reservoir MISSION PEAK REGIONAL PRESERVE APPIAN KENNEDY GROVE 19TH ST. BART/ 12TH ST. BART LAKE MERRITT BART FREMONT BART REGIONAL MACARTHUR BART UPTOWN TRANSIT WY. RECREATIONAL C A AREA CENTER MISSION PEAK S ADMIN. T CROW FAIRVIEW REGIONAL PT. WILSON R RD. ROC BLDG. PINOLE RD. O KHUR PRESERVE REDWOOD ST AV. 580 San Pablo Reservoir RD. MID. SCH. R APPIAN REDWOOD C MARKETPLACE AV. A RD. A N PO MADISON N AMEND C RD. Y H O STONEBRAE RD. AV. N APPIAN 80 RD. A DR. ELEM. SCH. CENTER PINOLE VISTA RD. RD. CENTER DON CASTRO D. DAM R VIEW PROCTOR WY. CENTER Y SAN REDWOOD AITKEN AV. REGIONAL NAOMI DR. RD. COST RICHMOND PKWY. LE RD. EDDY ST. SHEILA ST. BLVD. OHLONE MONUMENT PEAK L V PABLO RD. FRUITVALE BART COMM. RECREATION E A A RD. SAN LEANDRO BART BAY FAIR BART HEYER N REGIONAL LL W & SR. CTR. COLLEGE I TRANSIT CENTER V EY VIE SAN PABLO AREA MISSION BRUHNES EASTMONT RD. P PRESERVE DR. WY. DAM WILLOW PARK SEAVIEW OLIVE HYDE AMPHITHEATER CREEKSIDE - RD. REDWOOD ACE COMM. CTR. RD. MID. SCH. A AV. OLINDA TRANSIT CENTER ST. GLEN ELLEN DR. Z PO PUBLIC SHAWN MISSION COLISEUM BART N DE ANZA/ DAM CENTER FremontA MAY PINEHURST DELTA GOLF COURSE NILES MUSEUM R PO AV. HIGH SCH. PABLO ANTHONY CHABOT W BLVD. O ANTHONY CHABOT O BRYANT OF LOCAL SAN O SKYLINE C N REGIONAL PARK D HISTORY RD.
    [Show full text]
  • The East Bay Hills Fire, Oakland-Berkeley, California
    U.S. Fire Administration/Technical Report Series The East Bay Hills Fire Oakland-Berkeley, California USFA-TR-060/October 1991 U.S. Fire Administration Fire Investigations Program he U.S. Fire Administration develops reports on selected major fires throughout the country. The fires usually involve multiple deaths or a large loss of property. But the primary criterion T for deciding to do a report is whether it will result in significant “lessons learned.” In some cases these lessons bring to light new knowledge about fire--the effect of building construction or contents, human behavior in fire, etc. In other cases, the lessons are not new but are serious enough to highlight once again, with yet another fire tragedy report. In some cases, special reports are devel- oped to discuss events, drills, or new technologies which are of interest to the fire service. The reports are sent to fire magazines and are distributed at National and Regional fire meetings. The International Association of Fire Chiefs assists the USFA in disseminating the findings throughout the fire service. On a continuing basis the reports are available on request from the USFA; announce- ments of their availability are published widely in fire journals and newsletters. This body of work provides detailed information on the nature of the fire problem for policymakers who must decide on allocations of resources between fire and other pressing problems, and within the fire service to improve codes and code enforcement, training, public fire education, building technology, and other related areas. The Fire Administration, which has no regulatory authority, sends an experienced fire investigator into a community after a major incident only after having conferred with the local fire authorities to insure that the assistance and presence of the USFA would be supportive and would in no way interfere with any review of the incident they are themselves conducting.
    [Show full text]
  • 2020 Performance Report Transportation and Covid-19 in Alameda County
    2020 Performance Report Transportation and Covid-19 in Alameda County Prepared by: Alameda County Transportation Commission February 2021 Contents About the 2020 Performance Report ........................................................................... 1 Before COVID: Transportation in 2019 ......................................................................... 3 2020: A Year Like No Other .......................................................................................... 5 Transit in 2020 ................................................................................................................ 6 Goods Movement in 2020 ............................................................................................ 9 Roads and Congestion in 2020 .................................................................................. 10 Active Transportation in 2020 ..................................................................................... 12 Opportunities and Challenges .................................................................................. 14 2020 PERFORMANCE REPORT: TRANSPORTATION AND COVID-19 | Page i Page ii | ALAMEDA COUNTY TRANSPORTATION COMMISSION About the 2020 Performance Report Each year the Alameda County Transportation Commission (Alameda CTC) prepares a performance report to highlight the current state of the transportation system, key trends and changes in transportation, and what conditions are driving them. This report synthesizes the most recent data available for a variety of indicators to
    [Show full text]
  • Claremont Canyon
    Claremont Canyon voir ORINDA San Pablo Reser AD RO 24 PABLO DAM SAN FISH T Botanic RANCH EHURS Claremont and Blind (which became the University of California’s Huckleberry PIN D Garden ROAD Sibley Year opened: 1985 Acres: 208 ROA Volcanic Botanic Reg. Preserve ark Clark Kerr Campus). In the following few decades R. BL. Preserve Redwood K D AR . P Highlights: Hiking, horseback riding, connections Tilden Regional PaSrk. S D Regional P K Roberts . Y R the Park District acquired land eastward from many N L I D CY NE Regional T PEAK BL. CA R D N with UC Berkeley trails, good views west to S.F. IL Claremont E Rec. Area W H O Canyon individual landowners, the legacy of land subdivision Y P . Y Canyon Reg. RT N E I GRIZZL N H U R AV Preserve A S E Bay and the Golden Gate Bridge. BA C Q L “paper lots” sold door-to-door or by mail in the 1910s SPRUCE A IL BERKELEY JO M Did you know? Claremont Canyon was known for a 13 CLAREMONT V. L MARIN MARIN Regional Preserve I and 20s. In 1982 the Park District purchased a 64-acre O Temescal A XFORD N SHA P TELEGRAPH Reg.Rec. Area ARK C time as Telegraph Canyon because in 1858 it became AV TTUCK O . Y parcel covering most of Gwin Canyon, which com- L A GA . AV N W A the route for the first transcontinental telegraph. D V . OAKLAND . BL. pleted the preserve. A Berkeley, Oakland AV TER.
    [Show full text]
  • The Oakland-Berkeley Hills Fire of 19911
    PLENARY SESSION—ISSUES 6 USDA Forest Service Gen. Tech. Rep. PSW-GTR-158. 1995. The Biswell Symposium: Fire Issues and Solutions in Urban Interface and Wildland Ecosystems Plenary Session—Issues The Oakland-Berkeley Hills Fire of 19911 P. Lamont Ewell2 unday, October 20, 1991, will be remembered as the night. Fire crews had returned that morning to check for any Sdate of America’s most costly urban-wildland fire (FEMA hot spots and to pick up equipment, and were on the scene 1992) and one of the worst fires involving loss of life and for 2 hours before the fire suddenly escaped the area of property since the Great San Francisco Earthquake and Fire origin because of high winds. of 1906 (OFD 1992). Eyewitness accounts testify that a sole ember blew into The magnitude and range of what is simply referred to a tree just outside the burn area, and the tree exploded into as the “Tunnel Fire” is far beyond the experience of any flames. The resulting fire was quickly out of control—raging living American firefighter. Only those who fought the around and over firefighters who were suddenly fighting for Chicago Fire last century and those who battled the Great their lives. Over the course of the next several days, the fire Fire in San Francisco would be able to identify with this would leave 25 dead, 150 injured, and a total of 3,810 conflagration and firestorm. dwelling units destroyed. The fire, which burned over 1,500 A firestorm is defined as a fire which creates its own acres within an area of 5.25 square miles, would result in weather.
    [Show full text]
  • RM2 Capital Projects Summary
    Appendix A-1 Regional Measure 2 - Capital Program Project List RM2 Deliv. Capital Funding Segment Project No. ($1,000) No. Project Description Sponsor/ Implementing Agency 1 $ 3,000 1 BART/MUNI Access on Market Street Corridor BART 2 $ 30,000 2 SF MUNI Metro 3rd Street LRT Extension SF MUNI 3.1 SF MUNI E-Line - Acquire 11 Historic Streetcars SF MUNI 3 $ 10,000 3.2 SF MUNI E-Embarcadero Line Rehab 5 Double ended Vehicles SF MUNI 4.1 Dumbarton Commuter Rail Service San Mateo TA, ACCMA, ACTIA 4 $ 9,057 4.2 Union City Intermodal Station Environmental Impact Report Union City 4.3 ROW Acquisition Strategy ACTC 5 $ 26,000 5 Vallejo Ferry Intermodal Station City of Vallejo 6.1 Solano County Express Bus Intermodal Facilities - Vallejo Curtola Transit Center STA/ City of Vallejo 6.2 Solano Co. Express Bus Intermodal Facilities - Benicia Intermodal Facility STA/ City of Benicia 6 $ 12,251 6.3 Solano Co. Express Bus Intermodal Facilities - Fairfield Transporation Center STA/ Fairfield/Suisun Transit 6.4 Solano Co. Express Bus Intermodal Facilities - Vacaville Intermodal Station STA/ City of Vacaville 7.1 Solano North Connector (Abernathy to Green Valley Road) STA 7.2 Solano I-80/I-680 Interchange Complex (HOV Lanes from SR12 W to Airbase Parkway) STA 7 $ 100,000 7.3 I-80/I-680/SR-12 Interchange in Solano County STA 7.4 I-80 Eastbound Cordelia Truck Scales Relocation STA 7.5 I-80 High Occupancy / Express Lanes STA 8 $ 37,175 8 I-80 EB HOV Lane Extension from Route 4 to Carquinez Bridge Caltrans 9 $ 3,850 9 Richmond Parkway Park & Ride AC Transit 10.1 Cal Park Hill Tunnel Rehabilitation and Bikeway SMART 10.2 SMART Initial Operating Segment SMART 10 $ 56,500 10.3 SMART Seventh Train Set SMART 10.4 SMART Extension to Larkspur SMART 11.1 U.S.
    [Show full text]
  • Ground Transportation to the Walnut Creek Marriott
    Ground Transportation to the Walnut Creek Marriott ◆ BART (Bay Area Rapid Transit) ◆ Hours of operation: Monday through Friday 4:00 AM - Midnight Saturday 6:00 AM - Midnight Sunday 8:00 AM - Midnight From San Francisco International Airport: The BART Station is located in the International Terminal. There’s a free AirTrain to the BART Station from Terminals 1, 2, and 3. Take the Pittsburg/Bay Point train, and exit at the Walnut Creek BART Station. From Oakland International Airport: Take the AirBART shuttle service to the Coliseum BART station. At the Coliseum Station take the Richmond train. Transfer at the Oakland City Center/12th Street station to the Pittsburg/Bay Point train. Exit at the Walnut Creek BART Station. If you need the hotel shuttle to pick you up at the Walnut Creek BART station and bring you to the hotel, call our Bell Desk when you arrive, at (925) 934-2000. For additional BART fare or schedule information, call (925) 676-2278 or go to www.bart.gov. ◆ Airport Shuttle Service ◆ Reservations are required! East Bay Connection (800) 675-3278 www.eastbayconnection.net A-1 Express Shuttle (888) 698-2663 ◆ Towncar & Limousine Service ◆ Butler Limousine Services (866) 789-0340 www.butlerlimousineservices.com Ariana Limousine (925) 680-1010 RV Sedan & Limousine Service (510) 783-7260 Bay Magic Tours (925) 932-8687 www.baymagictours.com (For group transportation and local area tours) ◆ Local Taxi Service ◆ City Cab (925) 672-4400 East Bay Cab (925) 280-7200 ◆ 2355 North Main Street, Walnut Creek, California, 94596 ◆ 925-934-2000 Fax 925-933-6043 www.WalnutCreekMarriott.com Directions to the Walnut Creek Marriott Driving From San Francisco: Take US 101 to I-80 East “Sacramento” and cross the Bay Bridge.
    [Show full text]
  • Initial Study: Caldecott Improvement Project
    Initial Study: Caldecott Improvement Project On Route ALA/CC 24 From: ALA 24 KP 6.4 (PM 4.0) To: CC 24 KP 3.7 (PM 2.3) Caltrans Contract No. 04a1394 Lead Agency: California Department of Transportation 111 Grand Avenue Oakland, CA 94612-3006 Contact: Leo Scott (510) 286-5546 John Webb Date Leo Scott Date Division Chief Acting Division Chief North Region Environmental Planning Project Management - East Region California Department of Transportation California Department of Transportation, District 4 November 2002 California Department of Transportation. 2002. Initial study: Caldecott Improvement Project. November. (J&S 02-301) Oakland, CA. Prepared for Parsons Brinckerhoff by Jones & Stokes, Sacramento, CA. Contents Chapter 1. Introduction and Project Description ...............................................1-1 Introduction .......................................................................................1-1 Background.................................................................................1-1 Existing Conditions .....................................................................1-2 Project Location ................................................................................1-3 Project Description............................................................................1-3 Project Alternatives.....................................................................1-3 Purpose and Need............................................................................1-4 Chapter 2. Environmental Checklist....................................................................2-1
    [Show full text]
  • 2019 Annual Report: Sustainability
    2019 Annual Report: Sustainability San Francisco Bay Area Rapid Transit District GM Message I’m pleased to present to you BART’s 2019 Annual Report: Sustainability. This document comes at a time of daunt- ing challenges and unequaled uncertainty. Nevertheless, BART’s mission to provide safe, reliable, clean, and quality transit service for riders remains unchanged. BART is widely recognized as an environmental leader through its advancement of regional sustainability and improved public health outcomes. In the following pages, we think you will see that BART is making important strides in addressing climate change, environmental justice, and the housing crisis. BART is far more than trains and tracks. The District, now operating in five Bay Area counties, includes real estate assets that can be used to catalyze transit-oriented development. BART leverages these opportunities by working in partnership with the communities we serve in order to implement our regional land use vision and achieve local and regional economic development goals. Additionally, BART has made improvements that help BART customers access our stations via sustainable forms of transportation. Strengthening the connections between people, places, and services enhances BART’s value as a regional resource. The Coliseum Connections project is a shining example. This residential project has exceptional access to public transportation and is a true mixed-income property, with half its 110 apartment units designated as moderate- income rentals and half set aside as affordable housing for those making 50%-60% of the median income for Oakland. Also, consider that BART is one of Northern California’s largest consumers of electricity.
    [Show full text]
  • The Suburbanization of Manufacturing in the San Francisco Bay Area, 1850-1940
    INDUSTRY BUILDS OUT THE CITY: THE SUBURBANIZATION OF MANUFACTURING IN THE SAN FRANCISCO BAY AREA, 1850-1940 By Richard A. Walker Department of Geography University of California Berkeley, CA 94720 [email protected] Published version (with maps) in The Manufactured Metropolis edited by Robert Lewis Temple University Press 2004 pp. 92-123 ANYONE MAY DOWNLOAD AND USE THIS PAPER WITH THE USUAL COURTESY OF CITATION. COPYRIGHT 2004. 2 ABSTRACT The San Francisco Bay Area provides a clear example of industrial dispersal creating the sprawling form of the American metropolis. Neither change in transport modes nor residential suburbanization is principally responsible for shaping the outward spiral of urbanization. Manufacturing began its outward march from the outset of the city’s industrialization, establishing peripheral nodes of employment and working class residence within San Francisco, then beyond the city limits in South San Francisco and especially the East Bay. The primary cause of decentralization has been industrial shifts, or the outbreak of new activities in new places; these have normally taken the form of industrial districts, at various spatial scales. A second cause has been the orchestration of development by business leaders through property ownership and political maneuvering guided by a general vision of metropolitan expansion (whether in cooperation or competition with one another). List of Figures 1. Bay Area manufacturing (employment & output), 1860-1940 2. Bird’s eye view of San Francisco -- lithograph by Currier & Ives, c. 1880 3. Schematic map of industrial zones of San Francisco, c. 1890 4. Bird’s eye view of Bay Area -- San Francisco Daily Commercial News, c.
    [Show full text]