DOCSLIB.ORG

Parallel Balanced Binary Trees in Shared-Memory

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Parallel Balanced Binary Trees in Shared-Memory Parallel Balanced SPAA2020 Tutorial Binary trees in Shared-Memory Yihan Sun University of California, Riverside What’s in this tutorial • Algorithms and implementation details about parallel balanced binary trees (P-trees) • Simple with various functionalities • An open-source parallel library (PAM) and example code to use it • Applications that can be solved using the algorithms and the library in this tutorial 2 [Sedgewick and Wayne] Sec. 3.2 Binary Search Trees Trees Sec. 3.3 Balanced Search Trees • Trees are fundamental data structures for organizing data • Taught in entry-level [TAOCP] 2.3 Trees undergraduate courses 6.2.2. Binary Tree Searching 6.2.3. Balanced Trees 6.2.4. Multiway Trees • In real-world applications, things are more complicated… [CLRS] Especially in parallel 12 Binary Search Trees 13 Red-Black Trees 14.3 Interval trees 3 Applications Using Trees Document Search Engine Struct Doc { int l; Find information about pair<Word, Weight>* w; “balanced” and “binary” }; class doc_tree { Balanced AND Binary void build(Doc* d); Doc_set search(Word w); 1,234,567 results Doc_set and_search(Word* w); Doc 1: Balanced binary tree Doc_set or_search(Word* w); A binary tree is balanced if it void add_doc(Doc d); keeps its height small … …… Doc 2: AVL tree }; AVL tree is a balanced binary search tree structure … Searching and updating may need to be done concurrently Applications using trees Databases Find all young CS Struct Student { students with good grade id name, grade, age, major, … }; select class database { name void build(Doc* d); from Student* search(int id); students Student* fitler(function f); where void add_student(Student s); age < 25 …… and major = ‘CS’ }; and grade >= ‘A’ 5 Applications Using Trees Geometric queries (A 2D range query) struct Point { Find average temperature X x; Y y; Weight w; in Riverside }; class range_tree { void build(Point* p); Double ave_weight_search(X x1, X x2, Y y1, Y y2); int count_search(X x1, X x2, Y y1, Y y2); int list_all_search(X x1, X x2, Y y1, Y y2); Riverside void insert(Point p); range_tree filter(func f); Point* output(); void update(X x, Y y, Weight w); }; Balanced Binary Trees • Binary: each tree node has at most two children • Balanced: the tree has bounded height • Usually 푂(log 푛) for size 푛 A wild balanced hyphaene compressa binary tree 7 Balanced Binary Trees • Binary: each tree node has at most two children • Balanced: the tree has bounded height • Usually 푂(log 푛) for size 푛 A wild balanced binary tree 8 Balanced Binary Trees • Binary: each tree node has at most two children • Balanced: the tree has bounded height • Usually 푂(log 푛) for size 푛 An abstract balanced binary tree 9 Balanced Binary Trees • Balancing schemes: invariants to keep the tree balanced and to bound the tree height • We discuss four standard balancing schemes Height balanced Size balanced Randomized balanced Red- Weight- AVL black balanced Treaps Trees Trees Trees 10 Applications Using Trees Document Search Engine Databases Geometric queries Find information about Find all young CS (A 2D range query) “balanced” and “binary” students with good Find average temperature grade in Riverside area: 62 F BalancedlANDlBinary Eleganceselect – Framework 1,234,567 results Genericlfor balancingname schemes Doc 1: Balancedlbinary treeGenericiforfromapplications A binary tree is balanced if it students keeps its height small … Massivewhere Data - Performance Doc 2: AVL tree age < 25 Parallelism and concurrency AVL tree is a balanced binary and major = ‘CS’ Riverside search tree structure … Efficiency bothand in grade theory >= ‘A’and in practice Comprehensive Queries – Functionality Range queries, bulk updates, … What we want Augmentation, … Dynamicity, multi-versioning, … 11 What does P-tree look like? Elegance • Genericlfor balancing schemes Framework • Genericifor applications Massive Data Performance • Parallelism and concurrency • Efficiency both in theory and in practice Functionality Comprehensive Queries • Range queries, bulk updates, … • Augmentation, … Join • Dynamicity, multi-versioning, … (A primitive for trees) 12 1 Genericlfor balancing schemes All algorithms except join are identical across balancing schemes One algorithm for multiple balancing schemes! 2 Genericifor applications Multiple applications based on the same tree structure One tree for different problems! A primitive for trees: Join 13 The Primitive Join • 푇 =Join(푇퐿, 푒, 푇푅) : 푇퐿 and 푇푅 are two trees of a certain balancing scheme, 푒 is an entry/node (the pivot). • 푻푳 < 풆 < 푻푹 • It returns a valid tree 푇, which is 푇퐿 ∪ 푒 ∪ 푇푅 푇퐿 푇 푒4 푅2 푇 = 2 10 푒 푇푅 푇퐿 (Rebalance if necessary) 14 The Primitive Join 4 2 10 8 12 1 3 6 9 11 13 5 7 14 푇퐿 푒 푇푅 15 The Primitive Join • Connect at a balancing point 10 4 8 12 2 6 9 11 13 1 3 5 7 14 Balanced! 16 The Primitive Join • Connect at a balancing point 10 8 12 9 11 4 13 2 6 14 1 3 5 7 17 The Primitive Join • Connect at a balancing point • Rebalance (specific to balancing schemes) • Join algorithms for four balancing schemes and the cost bound [SPAA’16] 10 4 12 2 8 11 13 1 3 6 9 14 5 7 18 How does Join help? Applications 1 Algorithms Using Join Experiments • Generic across balancing schemes • Highly-Parallel • Theoretically efficient 2 Augmentation Using Join • A unified framework for augmentation • Model multiple applications 3 Persistence Using Join • Multi-versioning on trees 19 PART 1 Algorithms Using Join Generic algorithms across balancing schemes Parallel algorithms using divide-and-conquer paradigm Theoretically efficient 20 Join-based insertion 21 Join-based Algorithms: insertion insert(푻, 풌) CompareInsert if 푇 = ∅ then return Singleton(푘) 4 else let 퐿, 푘′, 푅 = 푇 if 푘 < 푘′ then 5 return Join (Insert(퐿, 푘),푘′,푅) else if 푘 > 푘(푇) then 2 9 return Join (퐿, 푘′, Insert(푅, 푘)) 1 3 else return 푇 Join-based Algorithms: insertion insert(푻, 풌) Join results if 푇 = ∅ then return Singleton(푘) (rebalanced may else let 퐿, 푘′, 푅 = 푇 be required) if 푘 < 푘′ then 5 return Join (Insert(퐿, 푘),푘′,푅) else if 푘 > 푘(푇) then 2 9 return Join (퐿, 푘′, Insert(푅, 푘)) 1 3 else return 푇 4 Join-based Algorithms: insertion insert(푻, 풌) Join results if 푇 = ∅ then return Singleton(푘) (rebalanced may else let 퐿, 푘′, 푅 = 푇 be required) if 푘 < 푘′ then 3 Join will return Join (Insert(퐿, 푘),푘′,푅) 2 5 rebalance else if 푘 > 푘(푇) then for Insert! return Join (퐿, 푘′, Insert(푅, 푘)) 1 4 9 else return 푇 푂(log 푛) Join-based split and Join2 25 The Inverse of Join: Split 25 13 51 • ⟨푻푳, 풃, 푻푹⟩ =Split (푻, 풌) • 푇퐿: all keys in 푇 < 푘 8 17 36 80 • 푇푅: all keys in 푇 > 푘 • A bit 푏 indicating whether 푘 ∈ 푇 5 12 15 22 30 42 70 95 22 Split by 42 13 30 70 8 17 22 36 푏 = 푡푟푢푒 51 80 5 12 15 95 푇퐿 푇푅 The Inverse of Join: Split split(푻, 풌) if 푇 = ∅ then return (∅, 퐟퐚퐥퐬퐞, ∅); 푘 ? 푘′ else { 푘′ = key at the root of 푇 if 푘 = 푘′ then { // same key as the root 푇퐿 = 푇. left; 푇푅 = 푇. right; flag = true} if 푘 < 푘′ then { // split the left subtree 푇. right (퐿, flag, 푅) = split(푇. left, 푘); 퐿 푅 푇퐿 = 퐿; 푇푅 = Join (푅, 푘′, 푇. right); } if 푘 > 푘′ then { /* symmetric*/ } 푇퐿 = 퐿 return (푇퐿, flag, 푇푅) ′ 푇푅 = join (푅, 푘 , 푇. 푟푔ℎ푡) 27 Another helper function: join2 • join2(푻푳, 푻푹) • Similar to join, but without the middle key • Can be done by first split out the last key in 푻푳, then use it to join the rest of 푻푳 and 푻푹 join2(푇퐿, 푇푅) { ′ u v (푇퐿, 푘) = split_last(푇퐿); ′ return join(푇퐿, 푘, 푇푅);} 푇퐿 푇푅 k Other Join-based algorithms 29 BST Algorithms • BST algorithms using divide-and-conquer scheme • Recursively deal with two subtrees (possibly in parallel) • Combine results of recursive calls and the root (e.g., using join or join2) • Usually gives polylogarithmic bounds on span func(T, …) { if (T is empty) return base_case; M = do_something(T.root); in parallel: L=func(T.left, …); R=func(T.right, …); return combine_results(L, R, M, …) } Get the maximum value • In each node we store a key and a value. The nodes are sorted by the keys. get_max(Tree T) { if (T is empty) return −∞; in parallel: L=get_max(T.left); R=get_max(T.right); return max(max(L, T.root.value), R); 푂(푛) work and 푂(log 푛) span Similar algorithm work on any map-reduce function Map and reduce • Maps each entry on the tree to a certain value using function map, then reduce all the mapped values using reduce (with identity identity). • Assume map and reduce both have constant cost. map_reduce(Tree T, function map, function reduce, value_type identity) { if (T is empty) return identity; M=map(t.root); in parallel: L=map_reduce(T.left, map, reduce, identity); R=map_reduce(T.right, map, reduce, identity); return reduce(reduce(L, M), R); 푂(푛) work and 푂(log 푛) span Filter • Select all entries in the tree that satisfy function 푓 • Return a tree of all these entries filter(Tree T, function f) { if (T is empty) return an empty tree; in parallel: L=filter(T.left, f); R=filter(T.right, f); if (f(T.root)) return join(L, T.root, R); else return join2(L, R); } 푂(푛) work and 푂(log2 푛) span Construction T=build(Array A, int size) { 푂(푛 log 푛) work and 퐴′=parallel_sort(A, size); 푂(log 푛) span, ′ return build_sorted(퐴 , 푠); bounded by the } sorting algorithm T=build_sorted(Arrary A, int start, int end) { if (start == end) return an empty tree; if (start == end-1) return singleton(A[start]); mid = (start+end)/2; 푂(푛) work and in parallel: 푂(log 푛) span L = build_sorted(A, start, mid); R = build_sorted(A, mid+1, end); return join(L, A[mid], R); Output to array • Output the entries in a tree 푇 to an array in its in-order • Assume each tree node stores its subtree size (an empty tree has size 0) to_array(Tree T, array A, int offset) { 풆 if (T is empty) return; A[offset+T.left.size] = get_entry(T.root); in parallel: 푇.
Load more

Recommended publications
  • Interval Trees Storing and Searching Intervals
    Interval Trees Storing and Searching Intervals • Instead of points, suppose you want to keep track of axis-aligned segments: • Range queries: return all segments that have any part of them inside the rectangle. • Motivation: wiring diagrams, genes on genomes Simpler Problem: 1-d intervals • Segments with at least one endpoint in the rectangle can be found by building a 2d range tree on the 2n endpoints. - Keep pointer from each endpoint stored in tree to the segments - Mark segments as you output them, so that you don’t output contained segments twice. • Segments with no endpoints in range are the harder part. - Consider just horizontal segments - They must cross a vertical side of the region - Leads to subproblem: Given a vertical line, find segments that it crosses. - (y-coords become irrelevant for this subproblem) Interval Trees query line interval Recursively build tree on interval set S as follows: Sort the 2n endpoints Let xmid be the median point Store intervals that cross xmid in node N intervals that are intervals that are completely to the completely to the left of xmid in Nleft right of xmid in Nright Another view of interval trees x Interval Trees, continued • Will be approximately balanced because by choosing the median, we split the set of end points up in half each time - Depth is O(log n) • Have to store xmid with each node • Uses O(n) storage - each interval stored once, plus - fewer than n nodes (each node contains at least one interval) • Can be built in O(n log n) time. • Can be searched in O(log n + k) time [k = #
    [Show full text]
  • Neuron C Reference Guide Iii • Introduction to the LONWORKS Platform (078-0391-01A)
    Neuron C Provides reference info for writing programs using the Reference Guide Neuron C programming language. 078-0140-01G Echelon, LONWORKS, LONMARK, NodeBuilder, LonTalk, Neuron, 3120, 3150, ShortStack, LonMaker, and the Echelon logo are trademarks of Echelon Corporation that may be registered in the United States and other countries. Other brand and product names are trademarks or registered trademarks of their respective holders. Neuron Chips and other OEM Products were not designed for use in equipment or systems, which involve danger to human health or safety, or a risk of property damage and Echelon assumes no responsibility or liability for use of the Neuron Chips in such applications. Parts manufactured by vendors other than Echelon and referenced in this document have been described for illustrative purposes only, and may not have been tested by Echelon. It is the responsibility of the customer to determine the suitability of these parts for each application. ECHELON MAKES AND YOU RECEIVE NO WARRANTIES OR CONDITIONS, EXPRESS, IMPLIED, STATUTORY OR IN ANY COMMUNICATION WITH YOU, AND ECHELON SPECIFICALLY DISCLAIMS ANY IMPLIED WARRANTY OF MERCHANTABILITY OR FITNESS FOR A PARTICULAR PURPOSE. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior written permission of Echelon Corporation. Printed in the United States of America. Copyright © 2006, 2014 Echelon Corporation. Echelon Corporation www.echelon.com Welcome This manual describes the Neuron® C Version 2.3 programming language. It is a companion piece to the Neuron C Programmer's Guide.
    [Show full text]
  • Augmentation: Range Trees (PDF)
    Lecture 9 Augmentation 6.046J Spring 2015 Lecture 9: Augmentation This lecture covers augmentation of data structures, including • easy tree augmentation • order-statistics trees • finger search trees, and • range trees The main idea is to modify “off-the-shelf” common data structures to store (and update) additional information. Easy Tree Augmentation The goal here is to store x.f at each node x, which is a function of the node, namely f(subtree rooted at x). Suppose x.f can be computed (updated) in O(1) time from x, children and children.f. Then, modification a set S of nodes costs O(# of ancestors of S)toupdate x.f, because we need to walk up the tree to the root. Two examples of O(lg n) updates are • AVL trees: after rotating two nodes, first update the new bottom node and then update the new top node • 2-3 trees: after splitting a node, update the two new nodes. • In both cases, then update up the tree. Order-Statistics Trees (from 6.006) The goal of order-statistics trees is to design an Abstract Data Type (ADT) interface that supports the following operations • insert(x), delete(x), successor(x), • rank(x): find x’s index in the sorted order, i.e., # of elements <x, • select(i): find the element with rank i. 1 Lecture 9 Augmentation 6.046J Spring 2015 We can implement the above ADT using easy tree augmentation on AVL trees (or 2-3 trees) to store subtree size: f(subtree) = # of nodes in it. Then we also have x.size =1+ c.size for c in x.children.
    [Show full text]
  • Advanced Data Structures
    Advanced Data Structures PETER BRASS City College of New York CAMBRIDGE UNIVERSITY PRESS Cambridge, New York, Melbourne, Madrid, Cape Town, Singapore, São Paulo Cambridge University Press The Edinburgh Building, Cambridge CB2 8RU, UK Published in the United States of America by Cambridge University Press, New York www.cambridge.org Information on this title: www.cambridge.org/9780521880374 © Peter Brass 2008 This publication is in copyright. Subject to statutory exception and to the provision of relevant collective licensing agreements, no reproduction of any part may take place without the written permission of Cambridge University Press. First published in print format 2008 ISBN-13 978-0-511-43685-7 eBook (EBL) ISBN-13 978-0-521-88037-4 hardback Cambridge University Press has no responsibility for the persistence or accuracy of urls for external or third-party internet websites referred to in this publication, and does not guarantee that any content on such websites is, or will remain, accurate or appropriate. Contents Preface page xi 1 Elementary Structures 1 1.1 Stack 1 1.2 Queue 8 1.3 Double-Ended Queue 16 1.4 Dynamical Allocation of Nodes 16 1.5 Shadow Copies of Array-Based Structures 18 2 Search Trees 23 2.1 Two Models of Search Trees 23 2.2 General Properties and Transformations 26 2.3 Height of a Search Tree 29 2.4 Basic Find, Insert, and Delete 31 2.5ReturningfromLeaftoRoot35 2.6 Dealing with Nonunique Keys 37 2.7 Queries for the Keys in an Interval 38 2.8 Building Optimal Search Trees 40 2.9 Converting Trees into Lists 47 2.10
    [Show full text]
  • Search Trees
    Lecture III Page 1 “Trees are the earth’s endless effort to speak to the listening heaven.” – Rabindranath Tagore, Fireflies, 1928 Alice was walking beside the White Knight in Looking Glass Land. ”You are sad.” the Knight said in an anxious tone: ”let me sing you a song to comfort you.” ”Is it very long?” Alice asked, for she had heard a good deal of poetry that day. ”It’s long.” said the Knight, ”but it’s very, very beautiful. Everybody that hears me sing it - either it brings tears to their eyes, or else -” ”Or else what?” said Alice, for the Knight had made a sudden pause. ”Or else it doesn’t, you know. The name of the song is called ’Haddocks’ Eyes.’” ”Oh, that’s the name of the song, is it?” Alice said, trying to feel interested. ”No, you don’t understand,” the Knight said, looking a little vexed. ”That’s what the name is called. The name really is ’The Aged, Aged Man.’” ”Then I ought to have said ’That’s what the song is called’?” Alice corrected herself. ”No you oughtn’t: that’s another thing. The song is called ’Ways and Means’ but that’s only what it’s called, you know!” ”Well, what is the song then?” said Alice, who was by this time completely bewildered. ”I was coming to that,” the Knight said. ”The song really is ’A-sitting On a Gate’: and the tune’s my own invention.” So saying, he stopped his horse and let the reins fall on its neck: then slowly beating time with one hand, and with a faint smile lighting up his gentle, foolish face, he began..
    [Show full text]
  • Computational Geometry: 1D Range Tree, 2D Range Tree, Line
    Computational Geometry Lecture 17 Computational geometry Algorithms for solving “geometric problems” in 2D and higher. Fundamental objects: point line segment line Basic structures: point set polygon L17.2 Computational geometry Algorithms for solving “geometric problems” in 2D and higher. Fundamental objects: point line segment line Basic structures: triangulation convex hull L17.3 Orthogonal range searching Input: n points in d dimensions • E.g., representing a database of n records each with d numeric fields Query: Axis-aligned box (in 2D, a rectangle) • Report on the points inside the box: • Are there any points? • How many are there? • List the points. L17.4 Orthogonal range searching Input: n points in d dimensions Query: Axis-aligned box (in 2D, a rectangle) • Report on the points inside the box Goal: Preprocess points into a data structure to support fast queries • Primary goal: Static data structure • In 1D, we will also obtain a dynamic data structure supporting insert and delete L17.5 1D range searching In 1D, the query is an interval: First solution using ideas we know: • Interval trees • Represent each point x by the interval [x, x]. • Obtain a dynamic structure that can list k answers in a query in O(k lg n) time. L17.6 1D range searching In 1D, the query is an interval: Second solution using ideas we know: • Sort the points and store them in an array • Solve query by binary search on endpoints. • Obtain a static structure that can list k answers in a query in O(k + lg n) time. Goal: Obtain a dynamic structure that can list k answers in a query in O(k + lg n) time.
    [Show full text]
  • Navigation Techniques in Augmented and Mixed Reality: Crossing the Virtuality Continuum
    Chapter 20 NAVIGATION TECHNIQUES IN AUGMENTED AND MIXED REALITY: CROSSING THE VIRTUALITY CONTINUUM Raphael Grasset 1,2, Alessandro Mulloni 2, Mark Billinghurst 1 and Dieter Schmalstieg 2 1 HIT Lab NZ University of Canterbury, New Zealand 2 Institute for Computer Graphics and Vision Graz University of Technology, Austria 1. Introduction Exploring and surveying the world has been an important goal of humankind for thousands of years. Entering the 21st century, the Earth has almost been fully digitally mapped. Widespread deployment of GIS (Geographic Information Systems) technology and a tremendous increase of both satellite and street-level mapping over the last decade enables the public to view large portions of the 1 2 world using computer applications such as Bing Maps or Google Earth . Mobile context-aware applications further enhance the exploration of spatial information, as users have now access to it while on the move. These applications can present a view of the spatial information that is personalised to the user’s current context (context-aware), such as their physical location and personal interests. For example, a person visiting an unknown city can open a map application on her smartphone to instantly obtain a view of the surrounding points of interest. Augmented Reality (AR) is one increasingly popular technology that supports the exploration of spatial information. AR merges virtual and real spaces and offers new tools for exploring and navigating through space [1]. AR navigation aims to enhance navigation in the real world or to provide techniques for viewpoint control for other tasks within an AR system. AR navigation can be naively thought to have a high degree of similarity with real world navigation.
    [Show full text]
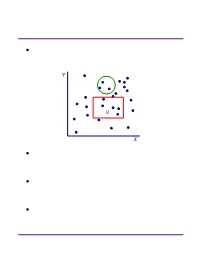
  • Range Searching
    Range Searching ² Data structure for a set of objects (points, rectangles, polygons) for efficient range queries. Y Q X ² Depends on type of objects and queries. Consider basic data structures with broad applicability. ² Time-Space tradeoff: the more we preprocess and store, the faster we can solve a query. ² Consider data structures with (nearly) linear space. Subhash Suri UC Santa Barbara Orthogonal Range Searching ² Fix a n-point set P . It has 2n subsets. How many are possible answers to geometric range queries? Y 5 Some impossible rectangular ranges 6 (1,2,3), (1,4), (2,5,6). 1 4 Range (1,5,6) is possible. 3 2 X ² Efficiency comes from the fact that only a small fraction of subsets can be formed. ² Orthogonal range searching deals with point sets and axis-aligned rectangle queries. ² These generalize 1-dimensional sorting and searching, and the data structures are based on compositions of 1-dim structures. Subhash Suri UC Santa Barbara 1-Dimensional Search ² Points in 1D P = fp1; p2; : : : ; png. ² Queries are intervals. 15 71 3 7 9 21 23 25 45 70 72 100 120 ² If the range contains k points, we want to solve the problem in O(log n + k) time. ² Does hashing work? Why not? ² A sorted array achieves this bound. But it doesn’t extend to higher dimensions. ² Instead, we use a balanced binary tree. Subhash Suri UC Santa Barbara Tree Search 15 7 24 3 12 20 27 1 4 9 14 17 22 25 29 1 3 4 7 9 12 14 15 17 20 22 24 25 27 29 31 u v xlo =2 x hi =23 ² Build a balanced binary tree on the sorted list of points (keys).
    [Show full text]
  • I/O-Efficient Spatial Data Structures for Range Queries
    I/O-Efficient Spatial Data Structures for Range Queries Lars Arge Kasper Green Larsen MADALGO,∗ Department of Computer Science, Aarhus University, Denmark E-mail: [email protected],[email protected] 1 Introduction Range reporting is a one of the most fundamental topics in spatial databases and computational geometry. In this class of problems, the input consists of a set of geometric objects, such as points, line segments, rectangles etc. The goal is to preprocess the input set into a data structure, such that given a query range, one can efficiently report all input objects intersecting the range. The ranges most commonly considered are axis-parallel rectangles, halfspaces, points, simplices and balls. In this survey, we focus on the planar orthogonal range reporting problem in the external memory model of Aggarwal and Vitter [2]. Here the input consists of a set of N points in the plane, and the goal is to support reporting all points inside an axis-parallel query rectangle. We use B to denote the disk block size in number of points. The cost of answering a query is measured in the number of I/Os performed and the space of the data structure is measured in the number of disk blocks occupied, hence linear space is O(N=B) disk blocks. Outline. In Section 2, we set out by reviewing the classic B-tree for solving one- dimensional orthogonal range reporting, i.e. given N points on the real line and a query interval q = [q1; q2], report all T points inside q. In Section 3 we present optimal solutions for planar orthogonal range reporting, and finally in Section 4, we briefly discuss related range searching problems.
    [Show full text]
  • Parallel Range, Segment and Rectangle Queries with Augmented Maps
    Parallel Range, Segment and Rectangle Queries with Augmented Maps Yihan Sun Guy E. Blelloch Carnegie Mellon University Carnegie Mellon University [email protected] [email protected] Abstract The range, segment and rectangle query problems are fundamental problems in computational geometry, and have extensive applications in many domains. Despite the significant theoretical work on these problems, efficient implementations can be complicated. We know of very few practical implementations of the algorithms in parallel, and most implementations do not have tight theoretical bounds. In this paper, we focus on simple and efficient parallel algorithms and implementations for range, segment and rectangle queries, which have tight worst-case bound in theory and good parallel performance in practice. We propose to use a simple framework (the augmented map) to model the problem. Based on the augmented map interface, we develop both multi-level tree structures and sweepline algorithms supporting range, segment and rectangle queries in two dimensions. For the sweepline algorithms, we also propose a parallel paradigm and show corresponding cost bounds. All of our data structures are work-efficient to build in theory (O(n log n) sequential work) and achieve a low parallel depth (polylogarithmic for the multi-level tree structures, and O(n) for sweepline algorithms). The query time is almost linear to the output size. We have implemented all the data structures described in the paper using a parallel augmented map library. Based on the library each data structure only requires about 100 lines of C++ code. We test their performance on large data sets (up to 108 elements) and a machine with 72-cores (144 hyperthreads).
    [Show full text]
  • Handwritten Digit Classication Using 8-Bit Floating Point Based Convolutional Neural Networks
    Downloaded from orbit.dtu.dk on: Apr 10, 2018 Handwritten Digit Classication using 8-bit Floating Point based Convolutional Neural Networks Gallus, Michal; Nannarelli, Alberto Publication date: 2018 Document Version Publisher's PDF, also known as Version of record Link back to DTU Orbit Citation (APA): Gallus, M., & Nannarelli, A. (2018). Handwritten Digit Classication using 8-bit Floating Point based Convolutional Neural Networks. DTU Compute. (DTU Compute Technical Report-2018, Vol. 01). General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain • You may freely distribute the URL identifying the publication in the public portal If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. Handwritten Digit Classification using 8-bit Floating Point based Convolutional Neural Networks Michal Gallus and Alberto Nannarelli (supervisor) Danmarks Tekniske Universitet Lyngby, Denmark [email protected] Abstract—Training of deep neural networks is often con- In order to address this problem, this paper proposes usage strained by the available memory and computational power. of 8-bit floating point instead of single precision floating point This often causes it to run for weeks even when the underlying which allows to save 75% space for all trainable parameters, platform is employed with multiple GPUs.
    [Show full text]
  • Lecture Notes of CSCI5610 Advanced Data Structures
    Lecture Notes of CSCI5610 Advanced Data Structures Yufei Tao Department of Computer Science and Engineering Chinese University of Hong Kong July 17, 2020 Contents 1 Course Overview and Computation Models 4 2 The Binary Search Tree and the 2-3 Tree 7 2.1 The binary search tree . .7 2.2 The 2-3 tree . .9 2.3 Remarks . 13 3 Structures for Intervals 15 3.1 The interval tree . 15 3.2 The segment tree . 17 3.3 Remarks . 18 4 Structures for Points 20 4.1 The kd-tree . 20 4.2 A bootstrapping lemma . 22 4.3 The priority search tree . 24 4.4 The range tree . 27 4.5 Another range tree with better query time . 29 4.6 Pointer-machine structures . 30 4.7 Remarks . 31 5 Logarithmic Method and Global Rebuilding 33 5.1 Amortized update cost . 33 5.2 Decomposable problems . 34 5.3 The logarithmic method . 34 5.4 Fully dynamic kd-trees with global rebuilding . 37 5.5 Remarks . 39 6 Weight Balancing 41 6.1 BB[α]-trees . 41 6.2 Insertion . 42 6.3 Deletion . 42 6.4 Amortized analysis . 42 6.5 Dynamization with weight balancing . 43 6.6 Remarks . 44 1 CONTENTS 2 7 Partial Persistence 47 7.1 The potential method . 47 7.2 Partially persistent BST . 48 7.3 General pointer-machine structures . 52 7.4 Remarks . 52 8 Dynamic Perfect Hashing 54 8.1 Two random graph results . 54 8.2 Cuckoo hashing . 55 8.3 Analysis . 58 8.4 Remarks . 59 9 Binomial and Fibonacci Heaps 61 9.1 The binomial heap .
    [Show full text]