Representing Things with Bits
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Ill[S ADJUSTMENTS
B249 DATA TRANSMISSION CONTROL UNIT INTRODUCTION AND OPERATION Burroughs FUNCTIONAL DETAIL FIELD ENGINEERING CIRCUIT DETAIL lJrn~[}{] ~ D~ill[s ADJUSTMENTS MAINTENANCE ~ ill ~ OD ill [S PROCEDURES INST ALLAT ION PROCEDURES RELIABILITY IMPROVEMENT NOTICES OPTIONAL FEATURES MODIFICATIONS (BRANCH LIBRARIES) Printed in U.S. America 9-15-66 Form 1026259 Burroughs - B249 Data Transmission ~echnical Manual I N D E X INTRODUCTION & OPERATION - SECTION I Page No. B249 Data Transmission Control Unit - General Descript ion . 1 Glossary - Data Transmission Terminal Unit and MCU. 5 Glossary - DTCU & System . 3 Physical De$cr1ption . 2 FUNCTIONAL DETAIL - SECTION II B300 Active Interrogate. · . · . · · 57 B300 Data Communications Read. · · . · · · · 62 B300 Data Communications Write · · . 78 B300 Passive Interrogate · · 49 VB300 Passive Interrogate - ITU (B486) Mode · . 92 v13300 Read - ITU (B486) Mode. · · . · · . · . 95 V'B300 Write - ITU (13486) Mode · · . · · 108 B5500 Data Communications Interrogate. · . 1 B5500 Data Communications Read . · 9 B5500 Data Communications Write. · 21 CIRCUIT DETAIL - SECTION III "AU Register Load - (Normal & Reverse) 1 Clock Control. ... 11 Scan . 3 Translator . 4 ADJUSTMENTS - SECTION IV Clock Adjustments ..... 1 Variable Bias Adjustment . 1 MAINTENANCE PROCEDURES - SECTION V Maintenance Panel ... 1 INSTALLATION PROCEDURES - SECTION VI DTCU Installation. 1 Pluggable Options. 2 Power ON . 3 Special Inquiry Terminal Connection .. 2 NOTE: Pages for Sections VII, VIII and IX will be furnished when applicable. Printed in U. S. America Revised 4/1/67 For Form 1026259 Burroughs - B249 Data Transmission Technical Manual Sec, I Page 1 Introduction & Operation B249 DATA TRANSMISSION CONTROL UNIT - GENERAL DESCRIPTION The B249 DTCU is required when: 1. More than one B487 DTTU is used on a single Processing System. -

Relink Eo 3-11-97
CHAPTER 1 COMMUNICATIONS As an Aviation Electronics Technician, you will be communication circuits. These operations are accom- tasked to operate and maintain many different types of plished through the use of compatible and flexible airborne communications equipment. These systems communication systems. may differ in some respects, but they are similar in many Radio is the most important means of com- ways. As an example, there are various models of AM municating in the Navy today. There are many methods radios, yet they all serve the same function and operate of transmitting in use throughout the world. This manual on the same basic principles. It is beyond the scope of will discuss three types. They are radiotelegraph, this manual to discuss each and every model of radiotelephone, and teletypewriter. communication equipment used on naval aircraft; therefore, only representative systems will be discussed. Every effort has been made to use not only systems that Radiotelegraph are common to many of the different platforms, but also have not been used in the other training manuals. It is Radiotelegraph is commonly called CW (con- the intent of this manual to have systems from each and tinuous wave) telegraphy. Telegraphy is accomplished every type of aircraft in use today. by opening and closing a switch to separate a continuously transmitted wave. The resulting “dots” and “dashes” are based on the Morse code. The major RADIO COMMUNICATIONS disadvantage of this type of communication is the relatively slow speed and the need for experienced Learning Objective: Recognize the various operators at both ends. types of radio communications. -

Ascii, Baudot, and the Radio Amateur
ASCII, BAUDOT AND THE RADIO AMATEUR George W. Henry, Jr. K9GWT Copyright © 1980by Hal Communications Corp., Urbana, Illinois HAL COMMUNICATIONS CORP. BOX365 ASCII, BAUDOT, AND THE RADIO AMATEUR The 1970's have brought a revolution to amateur radio RTTY equipment separate wire to and from the terminal device. Such codes are found in com and techniques, the latest being the addition of the ASCII computer code. mon use with computer and line printer devices. Radio amateurs in the Effective March 17, 1980, radio amateurs in the United States have been United States are currently authorized to use either the Baudot or ASCII authorized by the FCC to use the American Standard Code for Information serial asynchronous TTY codes. Interchange(ASCII) as well as the older "Baudot" code for RTTY com munications. This paper discusses the differences between the two codes, The Baudot TTY Code provides some definitions for RTTY terms, and examines the various inter facing standards used with ASCII and Baudot terminals. One of the first data codes used with mechanical printing machines uses a total of five data pulses to represent the alphabet, numerals, and symbols. Constructio11 of RTTY Codes This code is commonly called the Baudot or Murray telegraph code after the work done by these two pioneers. Although commonly called the Baudot Mark Ull s,.ce: code in the United States, a similar code is usually called the Murray code in other parts of the world and is formally defined as the International Newcomers to amateur radio RTTY soon discover a whole new set of terms, Telegraphic Alphabet No. -

Teletypewriter Communication Codes
Teletypewriter Communication Codes Gil Smith [email protected] 2001 (Document Notes) Abstract Preliminary -- 5/01 gil smith Corrections or comments to [email protected] This information is pulled from a variety of sources, such as various emails of the greenkeys group. For more discussion of teletypewriter code development, see: http://www.nadcomm.com/fiveunit/fiveunits.htm http://fido.wps.com/texts/codes/index.html http://www.science.uva.nl/faculteit/museum/DWcodes.html FIVE-UNIT CODES: USTTY and ITA2 (aka BAUDOT) There were a few variations in character codes for five-level teletypewriter machines. The two most-common character codes were ITA2 and USTTY (a variation of ITA2). The USTTY and ITA2 5-level teletypewriter codes are commonly referred to as "Baudot" codes. While this is technically incorrect, these popular 5-level codes evolved from the work of Jean Maurice Emile Baudot of France - - it seems fitting to accept the defacto reference to "Baudot" as implying USTTY or ITA2 codes, since they were the 5-level codes that saw practical use in teletypewriter systems. However, the true Baudot code dates to around 1874, when Baudot designed the "Baudot Multiplex System," a printing telegraph. The system used a 5-level code generated by a device with five keys, operated with two left-hand fingers, and three right-hand fingers -- this required great skill on the part of the operator who entered the code directly. However, it was still a major improvement in communications -- prior to Baudot's design, communication was carried out using Morse code with a telegraph key. The 5-level "Baudot" code was actually designed by Johann Gauss and Wilhelm Weber. -

Introduction to Computer Data Representation
Introduction to Computer Data Representation Peter Fenwick The University of Auckland (Retired) New Zealand Bentham Science Publishers Bentham Science Publishers Bentham Science Publishers Executive Suite Y - 2 P.O. Box 446 P.O. Box 294 PO Box 7917, Saif Zone Oak Park, IL 60301-0446 1400 AG Bussum Sharjah, U.A.E. USA THE NETHERLANDS [email protected] [email protected] [email protected] Please read this license agreement carefully before using this eBook. Your use of this eBook/chapter constitutes your agreement to the terms and conditions set forth in this License Agreement. This work is protected under copyright by Bentham Science Publishers to grant the user of this eBook/chapter, a non- exclusive, nontransferable license to download and use this eBook/chapter under the following terms and conditions: 1. This eBook/chapter may be downloaded and used by one user on one computer. The user may make one back-up copy of this publication to avoid losing it. The user may not give copies of this publication to others, or make it available for others to copy or download. For a multi-user license contact [email protected] 2. All rights reserved: All content in this publication is copyrighted and Bentham Science Publishers own the copyright. You may not copy, reproduce, modify, remove, delete, augment, add to, publish, transmit, sell, resell, create derivative works from, or in any way exploit any of this publication’s content, in any form by any means, in whole or in part, without the prior written permission from Bentham Science Publishers. 3. The user may print one or more copies/pages of this eBook/chapter for their personal use. -

(Düsseldorf, 1990): Volume VIII
This electronic version (PDF) was scanned by the International Telecommunication Union (ITU) Library & Archives Service from an original paper document in the ITU Library & Archives collections. La présente version électronique (PDF) a été numérisée par le Service de la bibliothèque et des archives de l'Union internationale des télécommunications (UIT) à partir d'un document papier original des collections de ce service. Esta versión electrónica (PDF) ha sido escaneada por el Servicio de Biblioteca y Archivos de la Unión Internacional de Telecomunicaciones (UIT) a partir de un documento impreso original de las colecciones del Servicio de Biblioteca y Archivos de la UIT. (ITU) ﻟﻼﺗﺼﺎﻻﺕ ﺍﻟﺪﻭﻟﻲ ﺍﻻﺗﺤﺎﺩ ﻓﻲ ﻭﺍﻟﻤﺤﻔﻮﻇﺎﺕ ﺍﻟﻤﻜﺘﺒﺔ ﻗﺴﻢ ﺃﺟﺮﺍﻩ ﺍﻟﻀﻮﺋﻲ ﺑﺎﻟﻤﺴﺢ ﺗﺼﻮﻳﺮ ﻧﺘﺎﺝ (PDF) ﺍﻹﻟﻜﺘﺮﻭﻧﻴﺔ ﺍﻟﻨﺴﺨﺔ ﻫﺬﻩ .ﻭﺍﻟﻤﺤﻔﻮﻇﺎﺕ ﺍﻟﻤﻜﺘﺒﺔ ﻗﺴﻢ ﻓﻲ ﺍﻟﻤﺘﻮﻓﺮﺓ ﺍﻟﻮﺛﺎﺋﻖ ﺿﻤﻦ ﺃﺻﻠﻴﺔ ﻭﺭﻗﻴﺔ ﻭﺛﻴﻘﺔ ﻣﻦ ﻧﻘﻼ ً◌ 此电子版(PDF版本)由国际电信联盟(ITU)图书馆和档案室利用存于该处的纸质文件扫描提供。 Настоящий электронный вариант (PDF) был подготовлен в библиотечно-архивной службе Международного союза электросвязи путем сканирования исходного документа в бумажной форме из библиотечно-архивной службы МСЭ. © International Telecommunication Union X V I I A . R DUSSGLDORF 21.5 - 1.6 1990 CCIR XVIIth PLENARY ASSEMBLY DUSSELDORF, 1990 INTERNATIONAL TELECOMMUNICATION UNION RECOMMENDATIONS OF THE CCIR, 1990 (ALSO RESOLUTIONS AND OPINIONS) VOLUME VIII MOBILE, RADIODETERMINATION, AMATEUR AND RELATED SATELLITE SERVICES v. CCIR 1. The International Radio Consultative Committee (CCIR) is the permanent organ of the International Telecommunication Union responsible under the International Telecommunication Convention "... to study technical and operating questions relating specifically to radiocommunications without limit of frequency range, and to issue recommendations on them../' (Inter national Telecommunication Convention, Nairobi 1982, First Part, Chapter I, Art. -

Character Encoding
Multilingualism on the Web Pascal Vaillant <[email protected]> IUT de Bobigny 1, rue de Chablis — 93017 Bobigny cedex www.iut-bobigny.univ-paris13.fr Writing systems IUT de Bobigny 1, rue de Chablis — 93017 Bobigny cedex www.iut-bobigny.univ-paris13.fr Writing systems • Mankind has been using speech for … as long as it deserves to be called human (definitory statement) e.g. 150 000 – 50 000 years (very approx) • It has been using writing since it has become organized in urban societies e.g. 5 000 years BP (approx) IUT de Bobigny 1, rue de Chablis — 93017 Bobigny cedex www.iut-bobigny.univ-paris13.fr Writing systems • Urban centres ⇒ specialization of economic units ⇒ currency ⇒ a central authority to control and organize ⇒ state and civil servants ⇒ taxes ⇒ accountancy ⇒ counting and writing IUT de Bobigny 1, rue de Chablis — 93017 Bobigny cedex www.iut-bobigny.univ-paris13.fr Development of writing systems • Highly probable origin: iconic (pictograms) • Examples (from Chinese): water: 水 (shuǐ) field: 田 (tián) mountain: 山 (shān) grass: 艸 (cǎo) fire: 火 (huǒ) beast: 豸 (zhì) horse: 馬 (mǎo) ox: 牛 (niú) IUT de Bobigny 1, rue de Chablis — 93017 Bobigny cedex www.iut-bobigny.univ-paris13.fr Development of writing systems • Combination → ideograms • Example (from Chinese): field: 田 (tián) grass: 艸 (cǎo) sprout: 苗 (miáo) IUT de Bobigny 1, rue de Chablis — 93017 Bobigny cedex www.iut-bobigny.univ-paris13.fr Development of writing systems • Rebus → ideophonograms • Example (from Chinese): ten thousands: 萬 (wàn) (orig. scorpion) sprout: 苗 -

Control Data® 3276-A Communication Terminal Controller
:£-oHT-ROl-BAIA CORPORATION CONTROL DATA® 3276-A COMMUNICATION TERMINAL CONTROLLER REFERENCE MANUAL March 8, 1'1bb Ed Salter K. M. Lampert 3271:. Manuals Reference manuals for the 3276 Multiplexor are in short supply; single copies have been mailed to you and to John Henderson- IDP is in the process of revising this publication and is reluctant to print additional copies of the present vera ion. Users of this manual are sometimes confused by a barrage of equipment numbers which are not rQlated to pricing manual numbers and descriptions. The 3276 is composed of the fol J04tJing units: - 1 8ltb5 flaster Mu I tip 1exor {MUX} 2 ~~binput steve nux 2 8167 Output Slave MUX The 321 Teletype Terminal Unit {TTU} is composed of the fo 1 low i 09 un its: 1: 85Xa Low Speed Input Unit {LSIU} ~ 85X9 Low Speed Output Unit {LSOU} The input/output units are selected to match the terminal equipment; 8508 LSIU~s and 8S0~ lSOU~$ are used with five level teletype and 8518 LSIU"s and 6519 lSOU"s are used with eight level teletypes- Other terminal units are used with higher speed equipment. K- ft. Lampert /dd cc: John Henderson ~ file CONTROL DATA CORPORATION CONTROL DATA® 3276-A COMMUNICATION TERMINAL CONTROLLER REFERENCE MANUAL Pub. No. 368 161 00 Record of Revisions REVISION NOTES Address comments concerning this manual to: Control Data Corporation Industrial Data Processing Div Technical Publications Section © 1965, Control Data Corporation 9549 Penn Avenue So. Printed in the United States of America Minneapolis, Minnesota 55431 CONTENTS 3276-A COMMUNICATION -
Table of Contents Item Transcript
DIGITAL COLLECTIONS ITEM TRANSCRIPT Zalman Grinberg. Full, unedited interview, 2012 ID FL007.interview PERMALINK http://n2t.net/ark:/86084/b4j09w657 ITEM TYPE VIDEO ORIGINAL LANGUAGE RUSSIAN TABLE OF CONTENTS ITEM TRANSCRIPT ENGLISH TRANSLATION 2 CITATION & RIGHTS 11 2021 © BLAVATNIK ARCHIVE FOUNDATION PG 1/11 BLAVATNIKARCHIVE.ORG DIGITAL COLLECTIONS ITEM TRANSCRIPT Zalman Grinberg. Full, unedited interview, 2012 ID FL007.interview PERMALINK http://n2t.net/ark:/86084/b4j09w657 ITEM TYPE VIDEO ORIGINAL LANGUAGE RUSSIAN TRANSCRIPT ENGLISH TRANSLATION —Today is November 26, 2012. We are in Miami, meeting a veteran of the Great Patriotic War. Please introduce yourself. My name is Zalman Aronovich Gringerg. —When and where were you born? I was born on May 17, 1922, in the district seat of Chemerivtsi, Kamianets-Podilskyi Oblast, Ukraine [now Khmelnitskii Oblast]. —Until what age did you live in your home town? Until I was . seventeen. I began first grade when I turned seven. It was at a Jewish seven-year school. After graduating from that school, I began eighth grade at a Ukrainian high school, from which I also successfully graduated in 1939. I had an almost perfect report card except for one grade, which was just “good.” Because of this I had to take entrance exams to enroll at university. In 1939 I enrolled as a freshman at the Odessa [Odesa] Institute of Communications. I was a good student. I completed a year, went back home to visit my parents, and began my sophomore year. In 1940, on the orders of then Minister of Defense Timoshenko, I and my comrades at the institute were all conscripted. -

ED297505.Pdf
DOCUMENT RESUME ED 297 505 EC 210 356 AUTHOR Borden, Peter A., Ed.; Vanderheiden, Gregg C., Ed. TITLE Communication, Control, and Computer Access for Disabled and Elderly Individuals. ResourceBook 4: Update to Books I,2, and 3. INSTITUTION Wisconsin Univ., Madison. Trace Center. SPONS AGENCY National Inst. on Disability and Rehabilitation Research (ED/OSERS), Washington, DC. REPORT NO ISBN-0-945459-00-9 PUB DATE 88 GRANT G008300045 NOTE 385p.; A product of the Research and Pevelopment Center on Communications, Control, and Computer Access for Handicapped Individuals. For ResourceBooks 1-3, see ED 283 305-307. AVAILABLE FROM Trace Research and Development Center, S-151 Waisman Center, 1500 Highland Ave., Madison, WI 53705-2280 ($18.50). PUB TYPE Reference Materials Directories/Catalogs (132) EDRS PRICE MFO1 /PC16 Plus Postage. DESCRIPTORS *Accessibility (for Disabled); Braille; *Communication (Thought Transfer); Communication Aids (for Disabled); Computer Assisted Instruction; Computer Managed Instruction; Computer Printers; *Computer Software; *Disabilities; *Electronic Control; Input Output Devices; Keyboarding (Data Entry); Microcomputers; *Older Adults; Rehabilitation; Resources; Speech Synthesizers; Telecommunications IDENTIFIERS *Augmentative Communication Systems ABSTRACT This update to the three-volume first edition of the "Rehab/Education ResourceBook Series" describes special software and products pertaining to communication, control, and computer access, designed specifically for the needs of disabled and elderly people. The -

ASCII, Unicode, and in Between Douglas A. Kerr Issue 3 June 15, 2010 ABSTRACT the Standard Coded Character Set ASCII Was Formall
ASCII, Unicode, and In Between Douglas A. Kerr Issue 3 June 15, 2010 ABSTRACT The standard coded character set ASCII was formally standardized in 1963 and, in its “complete” form, in 1967. It is a 7-bit character set, including 95 graphic characters. As personal computers emerged, they typically had an 8-bit architecture. To exploit that, they typically came to use character sets that were “8-bit extensions of ASCII”, providing numerous additional graphic characters. One family of these became common in computers using the MS-DOS operating system. Another similar but distinct family later became common in computers operating with the Windows operating system. In the late 1980s, a true second-generation coded character set, called Unicode, was developed, and was standardized in 1991. Its structure provides an ultimate capacity of about a million graphic characters, catering thoroughly to the needs of hundreds of languages and many specialized and parochial uses. Various encoding techniques are used to represent characters from this set in 8- and 16-bit computer environments. In this article, we will describe and discuss these coded character sets, their development, their status, the relationships between them, and practical implications of their use. Information is included on the entry, in Windows computer systems, of characters not directly accessible from the keyboard. BEFORE ASCII As of 1960, the interchange of data within and between information communication and processing systems was made difficult by the lack of a uniform coded character set. Information communication in the traditional “teletypewriter” sense generally used a 5-bit coded character set, best described as the “Murray code” (although as a result of historical misunderstandings it is often called the “Baudot code”). -
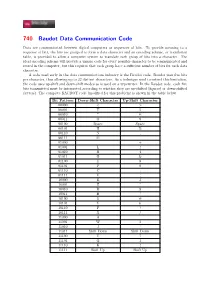
740 Baudot Data Communication Code
740 Baudot Data Communication Code Data are communicated between digital computers as sequences of bits. To provide meaning to a sequence of bits, the bits are grouped to form a data character and an encoding scheme, or translation table, is provided to allow a computer system to translate each group of bits into a character. The ideal encoding scheme will provide a unique code for every possible character to be communicated and stored in the computer, but this requires that each group have a sufficient number of bits for each data character. A code used early in the data communications industry is the Baudot code. Baudot uses five bits per character, thus allowing up to 32 distinct characters. As a technique used to extend this limitation, the code uses up-shift and down-shift modes as is used on a typewriter. In the Baudot code, each five bits transmitted must be interpreted according to whether they are up-shifted (figures) or down-shifted (letters). The complete BAUDOT code (modified for this problem) is shown in the table below. Bit Pattern Down-Shift Character Up-Shift Character 00000 < > 00001 T 5 00010 * @ 00011 O 9 00100 Space Space 00101 H % 00110 N , 00111 M . 01000 = + 01001 L ) 01010 R 4 01011 G & 01100 I 8 01101 P 0 01110 C : 01111 V ; 10000 E 3 10001 Z ” 10010 D $ 10011 B ? 10100 S # 10101 Y 6 10110 F ! 10111 X / 11000 A - 11001 W 2 11010 J ’ 11011 Shift Down Shift Down 11100 U 7 11101 Q 1 11110 K ( 11111 Shift Up Shift Up Universidad de Valladolid OJ: 740 – Baudot Data Communication Code 2/2 For example, the bit pattern 11111 represents up-shift and the bit pattern 11011 represents down- shift characters.