A Revisited Definition of the Three Solute Descriptors Related to the Van Der Waals Forces in Solutions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Investigating the Inhibition Mechanism of L,D-Transpeptidase 5 from Mycobacterium Tuberculosis Using Computational Methods
INVESTIGATING THE INHIBITION MECHANISM OF L,D-TRANSPEPTIDASE 5 FROM MYCOBACTERIUM TUBERCULOSIS USING COMPUTATIONAL METHODS BY: GIDEON FEMI TOLUFASHE 216076453 Submitted in fulfilment of the requirements for the degree of Doctor of Philosophy in Pharmaceutical Chemistry School of Health Sciences, College of Health Sciences, University of KwaZulu-Natal, Durban, South Africa. 2018 PREFACE The work described in this thesis was conducted at the Catalysis and Peptide Research Unit, Westville Campus, University of KwaZulu-Natal, Durban, South Africa, under the supervision of Dr Bahareh Honarparvar, Prof. H.G. Kruger and Dr G.E.M. Maguire. This work has not been submitted in any form for any degree or diploma to any institution, where use has been made of the work of others, it is duly acknowledged in the text. Supervisors: Dr B. Honarparvar Date 30/10/2018 Prof. H. G. Kruger________________ Date ___________ Dr. G.E.M Maguire_______________ Date ___________ As candidate’s supervisor I agree to the submission of this thesis. i DECLARATION DECLARATION I- PLAGIARISM I, Gideon Femi Tolufashe declare that (i). The research reports in this thesis, except where otherwise indicated, is my original work. (ii). This thesis has not been submitted for any degree or examination at any other university. (iii). This thesis does not contain other person’s data, pictures, graphs or other information, unless specifically acknowledged as being sourced from other persons. (iv). This thesis does not contain other person’s writing, unless specifically acknowledged as being sourced from other researchers. Where other written sources have been quoted, then: a. Their words have been re-written, but the general information attributed to them has been referenced. -

New Journal and Database Subscriptions – 2012 -2013
NEW JOURNAL AND DATABASE SUBSCRIPTIONS – 2012 -2013 New Journals Afterall: A Journal of Art, Context and Enquiry American Biology Teacher American Journal of Bioethics American Political Thought Annals of Tourism Research Art Documentation Biodiversity and Conservation Biomaterials Science BioScience Boom: A Journal of California California Archaeology California Management Review Catalysis Science & Technology Chemical Hazards in Industry China Journal Classical Antiquity Classical Philology Crime and Justice Critical Review of International Social and Political Philosophy Education in Chemistry Educational Technology Research Development Elephant Ethics Federal Sentencing Reporter Food & Function Frankie Gastronomica: The Journal of Food and Culture Haaretz Historical Studies in the Natural Sciences HOPOS: The Journal of the International Society for the History of Philosophy of Science Huntington Library Quarterly Indian Country Today Indonesia Journal Information, Communication & Society Innovation Policy and the Economy Integrative Biology Issues in Environmental Science and Technology Journal of Applied Remote Sensing Journal of Digital Media Management Journal of Empirical Research on Human Research Ethics Journal of Environmental Studies and Sciences Journal of Human Capital Journal of Labor Economics Journal of Leisure Research Journal of Micro/Nanolithography, MEMS, and MOEMS Journal of Modern History Journal of Nanophotonics Journal of North African Studies Journal of Palestine Studies Journal of Photonics for Energy Journal -

GUT RSC Journals List
SCHEDULE A Publisher Content Section A Customer has access to the electronic versions of the following journals via an External route: Access Post - Copyright Journals E-ISSN years cancellation Owner* during Term access Analyst 1364-5528 2008-2018 2012-2018 RSC Analytical Methods 1 1759-9679 2009-2018 2012-2018 RSC Annual Reports on the Progress of Chemistry, A 1460-4760 2008-2013 2012-2013 RSC B 1460 4779 2008-2013 2012-2013 RSC C 1460-4787 2008-2013 2012-2013 RSC Biomaterials Science 1 2047-4849 2013-2018 2016-2018 RSC Catalysis Science & Technology 1 2044-4761 2011-2018 2013-2018 RSC Chemical Communications 1364-548X 2008-2018 2012-2018 RSC Chemical Science 1, 2 2041-6539 2010-2014 2012-2014 RSC Chemical Society Reviews 1460-4744 2008-2018 2012-2018 RSC Chemistry World 1749-5318 2012-2016 2012-2016 RSC CrystEngComm 1466-8033 2008-2018 2012-2018 RSC Dalton Transactions 1477-9234 2008-2018 2012-2018 RSC Education in Chemistry 1749-5326 2012-2016 2012-2016 RSC Energy & Environmental Science 1 1754-5706 2008-2018 2012-2018 RSC Environmental Science: Nano 1 2051-8161 2014-2018 2016-2018 RSC Environmental Science: Processes & Impacts including 2050-7895 2013-2018 2013-2018 RSC Journal of Environmental Monitoring (1464-0333) 2008-2012 2012 Environmental Science: Water Research & Technology 1 2053-1419 2015-2018 2017-2018 RSC Faraday Discussions 1364-5498 2008-2018 2012-2018 RSC Food & Function 1 2042-650X 2010-2018 2012-2018 RSC Green Chemistry 1463-9270 2008-2018 2012-2018 RSC Inorganic Chemistry Frontiers 1 2052-1553 2014-2018 2017-2018 -
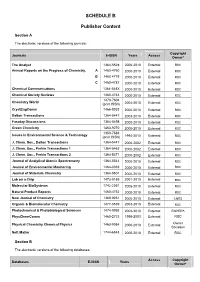
SCHEDULE B Publisher Content
SCHEDULE B Publisher Content Section A The electronic versions of the following journals: Copyright Journals E-ISSN Years Access Owner* The Analyst 1364-5528 2000-2010 External RSC Annual Reports on the Progress of Chemistry, A 1460-4760 2000-2010 External RSC B 1460 4779 2000-2010 External RSC C 1460-4787 2000-2010 External RSC Chemical Communications 1364-548X 2000-2010 External RSC Chemical Society Reviews 1460-4744 2000-2010 External RSC 1473-7604 Chemistry World (print ISSN) 2004-2010 External RSC CrystEngComm 1466-8033 2000-2010 External RSC Dalton Transactions 1364-5447 2003-2010 External RSC Faraday Discussions 1364-5498 2000-2010 External RSC Green Chemistry 1463-9270 2000-2010 External RSC 1350-7583 Issues in Environmental Science & Technology (print ISSN) 1994-2010 External RSC J. Chem. Soc., Dalton Transactions 1364-5447 2000-2002 External RSC J. Chem. Soc., Perkin Transactions 1 1364-5463 2000-2002 External RSC J. Chem. Soc., Perkin Transactions 2 1364-5471 2000-2002 External RSC Journal of Analytical Atomic Spectrometry 1364-5544 2000-2010 External RSC Journal of Environmental Monitoring 1464-0333 2000-2010 External RSC Journal of Materials Chemistry 1364-5501 2000-2010 External RSC Lab on a Chip 1473-0189 2001-2010 External RSC Molecular BioSystems 1742-2051 2005-2010 External RSC Natural Product Reports 1460-4752 2000-2010 External RSC New Journal of Chemistry 1369-9261 2000-2010 External CNRS Organic & Biomolecular Chemistry 1477-0539 2003-2010 External RSC Photochemical & Photobiological Sciences 1474-9092 2002-2010 -

1 Supporting Information Chemical Information Literacy at a Liberal Arts
Supporting Information Chemical Information Literacy at a Liberal Arts College George Greco Department of Chemistry Goucher College 1021 Dulaney Valley Road Baltimore, MD 21204 1 Table of Contents Course Syllabus 3-6 Handout 1: The Chemical Literature 7-8 Handout 2: Types of Papers 9 Handout 3: Citations 10-11 Handout 4: Secondary Sources 12-15 Handout 5: SciFinder 16-18 Handout 6: Free Public Databases 19-22 Handout 7: InChI and SMILES 23-25 Handout 8: Reaxys, Beilstein and Gmelin 26-27 Handout 9: Patents 28-32 Handout 10: Reading papers for current events 33 Handout 11: The publication process 34-37 Handout 12: Structure and sequence databases 38-41 Handout 13: Databases of Spectral and Thermodynamic Properties 42-43 HW #1: The Chemical Literature 44 SciFinder Assignment 45-46 HW #4: PubMed and PubChem 47 HW #5: SMILES and InChI 48 Current Events Assignment 49-50 Note about final exam 51 2 Chemistry 245 – Spring 2015 Chemical Information Literacy Instructor : Dr. George Greco Office : Hoffberger 220 Phone : 410-337-6313 Email : [email protected] Class Meetings : Tuesdays 11:45– 12:35 Hoffberger 223 Office hours: Monday 11:00-12:30, Wednesday 1:30-3:00 or by appointment (e-mail me) Optional Text : Chemical Information for Chemists: A Primer edited by Judith N. Currano and Dana L. Roth. Published by RSC Publishing. ISBN 978-1-84973-551-3 Disclaimer: This is the first time we are offering this course. It is my first time teaching a course like this. I don’t expect everything to go 100% smoothly. -

Royal Society of Chemistry(RSC/英国王立科学会)
Royal Society of Chemistry(RSC/英国王立科学会) 2017/4月 Notes Title Year 1 Analyst 1997-present 2 Analytical Abstracts 1980-present 3 Analytical Communications 1997-1999 4 Analytical Methods 2009-present 5 Annual Reports on the Progress of Chemistry, Sect. A 1997-2013 6 Annual Reports on the Progress of Chemistry, Sect. B 1997-2013 7 Annual Reports on the Progress of Chemistry, Sect. C 1997-2013 8 Biomaterials Science 2013-present 9 Catalysis Science & Technology 2010-present 10 Chemical Communications (Cambridge) 1997-present 11 Free Chemical Science 2010-present 12 Chemical Society Reviews 1997-present 13 Chemistry Education Research and Practice 2008-present 14 Contemporary Organic Synthesis 1997-1997 15 CrystEngComm 1999-present 16 Dalton Transactions 2003-present 17 Education in chemistry 2004-present 18 Energy & Environmental Science 2008-present 19 Environmental Science: Nano 2014-present 20 Environmental Science: Processes & Impacts 2013-present 21 Environmental Science: Water Research & Technology 2015-present 22 Faraday Discussions 1997-present 23 Food & Function 2010-present 24 Geochemical Transactions 2000-2003 25 Green Chemistry 1999-present 26 Integrative Biology 2009-present 27 e-book Issues in Environmental Science and Technology 1994-present 28 Journal of Analytical Atomic Spectrometry 1997-present 29 Journal of Chemical Research, Synopses 1997-1999 30 Journal of Environmental Monitoring 1999-2012 31 Journal of Materials Chemistry 1997-2012 32 Journal of Materials Chemistry A: Materials for energy and 2013-present sustainability -
Poly Ethylene Glycols As Efficient
Green and Sustainable Chemistry, 2011, 1, 132-148 doi:10.4236/gsc.2011.14022 Published Online November 2011 (http://www.SciRP.org/journal/gsc) Poly Ethylene Glycols as Efficient Media for the Synthesis of β-Nitro Styrenes from α, β-Unsaturated Carboxylic Acids and Metal Nitrates under Conventional and Non-Conventional Conditions Kamatala Chinna Rajanna1, Kola Ramesh2, Soma Ramgopal1, Somannagari Shylaja2, Pochampally Giridhar Reddy2, Pondichery Kuppuswamy Saiprakash1 1Department of Chemistry, Osmania University, Hyderabad, India 2Department of Chemistry, CBIT, Gandipet, Hyderabad, India E-mail: [email protected] Received August 18, 2011; revised October 14, 2011; accepted October 26, 2011 Abstract Poly ethylene glycols (PEG-200, 400, 600, 4000 and 6000) supported reactions were conducted with certain α, β-unsaturated acids in presence of metal nitrates under solvent free (solid state) and mineral acid free con- ditions. The reactants were ground in a mortar with a pestle for about 30 minutes. The aromatic acids under- went nitro decarboxylation and afforded β-nitro styrene derivatives in very good yield while α, β-unsaturated aliphatic carboxylic acids gave corresponding nitro derivatives. Addition of PEG accelerated rate of the reac- tion enormously. Reaction times substantially decreased from several hours to few minutes followed by highly significant increase in the product yield. Among the several PEGs PEG-300 has been found to be much more effective than other PEGs. Keywords: Poly Ethylene Glycols (PEG), Rate Accelerations, α, β-Unsaturated Acids, Metal Nitrates, Solvent Free (Solid State), β-Nitro Styrene Derivatives, α, β-Unsaturated Aliphatic Acids, Nitro Derivatives 1. Introduction via microwave irradiation has been the subject of interest for the past one decade which has the advantage of being The use of non volatile solvents is an essential ingredient eco-friendly, easy to handle, employ shorter reaction times in a large number of organic synthesis protocols, which and solvent less conditions. -

Electronic Access Licence Agreement
ELECTRONIC ACCESS LICENCE AGREEMENT This Agreement is made the Chemistry located at ("Publisher"} and Th offices at WHEREAS (A) Publisher holds journal articles and databases in electronic form; (B) Customer wishes to license access to journal articles and/or databases; and (C) Publisher agrees to grant such licence. NOW, THEREFORE, in consideration of the mutual promises set forth herein, the parties agree as follows: 1. Definitions In thisAgreement the following terms shall have the following meanings: "Authorised Users" means current employees (including faculty, staff, and independent contractors) of the Customer and students ofthe Customer who, in either case, have been allowed access to Publlsher Content by Customer, regardless of the physical location of such persons, such access shall be unlimited and shall be by Secure Authentication so that these users may access and use Publisher Content in accordance with the terms of this Agreement. Remote access by AuthorisedUsers to Publisher Content is allowed and Walk-In Users, i.e. persons who are permitted by the Customer to access Publisher Content whilst they are on Customer's physical premises. Such access must at all times be by Secure Authentication on computer terminals within the Customer's physical premises. Walk-In Users may not be given means to access Publisher Content outside the Customer's physical premises or by any wireless network unless the network is a secure network provided by the Customer. "Commercial Use" means use which is for direct monetary reward or commercial advantage, whether by or for Customer or Authorised User, by means of the sale, resale, loan, transfer, hire or other form of exploitation of Publisher Content. -

Crystaleye: Automated Aggregation, Semantification and Dissemination
Person to contact for this submission: Peter Murray-Rust ([email protected]; phone: 01223 336432; fax: 01223 763076) Journal of Applied Crystallography CIF applications Appendix A. Sources of data International Union of Crystallography (http://journals.iucr.org/) Acta Crystallographica Section A: Foundations of Crystallography (http://journals.iucr.org/a/) Acta Crystallographica Section B: Structural Science (http://journals.iucr.org/b/) Acta Crystallographica Section C: Crystal Structure Communications (http://journals.iucr.org/c/) Acta Crystallographica Section D: Biological Crystallography (http://journals.iucr.org/d/) Acta Crystallographica Section E: Structure Reports (http://journals.iucr.org/e/) Acta Crystallographica Section F: Structural Biology and Crystallization Communications (http://journals.iucr.org/f/) Journal of Applied Crystallography (http://journals.iucr.org/j/) Journal of Synchrotron Radiation (http://journals.iucr.org/s/) The Royal Society of Chemistry (http://pubs.rsc.org) Chemical Communications (http://pubs.rsc.org/en/Journals/JournalIssues/CC) CrystEngComm (http://pubs.rsc.org/en/Journals/JournalIssues/CE) Physical Chemistry and Chemical Physics (http://pubs.rsc.org/en/Journals/JournalIssues/CP) Dalton Transactions (http://pubs.rsc.org/en/Journals/JournalIssues/DT) Green Chemistry (http://pubs.rsc.org/en/Journals/JournalIssues/GC) Journal of Materials Chemistry (http://pubs.rsc.org/en/Journals/JournalIssues/JM) New Journal of Chemistry (http://pubs.rsc.org/en/Journals/JournalIssues/NJ) Organic and Biomolecular Chemistry -
RSC Gold Collection 2017 Excluding Journals Archive URL's Listing for 2017 Access Periodical E-ISSN Using DOI Openurl (V.0.1 Format) Openurl (V.1.0 Format) URL
RSC Gold Collection 2017 excluding Journals Archive URL's Listing for 2017 access Periodical e-ISSN Using DOI OpenURL (v.0.1 format) OpenURL (v.1.0 format) URL Analyst 1364-5528 http://dx.doi.org/10.1039/1364-5528/1876 http://xlink.rsc.org?genre=journal&eissn=1364-5528&date=1876 http://xlink.rsc.org?rft.genre=journal&rft.eissn=1364-5528&rft.date=1876 Analytical Methods 1759-9679 http://dx.doi.org/10.1039/1759-9679/2009 http://xlink.rsc.org?genre=journal&eissn=1759-9679&date=2009 http://xlink.rsc.org?rft.genre=journal&rft.eissn=1759-9679&rft.date=2009 Annual Reports on the Progress of Chemistry, Sect. A 1460-4760 http://dx.doi.org/10.1039/1460-4760/1979 http://xlink.rsc.org?genre=journal&eissn=1460-4760&date=1979 http://xlink.rsc.org?rft.genre=journal&rft.eissn=1460-4760&rft.date=1979 Annual Reports on the Progress of Chemistry, Sect. B 1460-4779 http://dx.doi.org/10.1039/1460-4779/1967 http://xlink.rsc.org?genre=journal&eissn=1460-4779&date=1967 http://xlink.rsc.org?rft.genre=journal&rft.eissn=1460-4779&rft.date=1967 Annual Reports on the Progress of Chemistry, Sect. C 1460-4787 http://dx.doi.org/10.1039/1460-4787/1979 http://xlink.rsc.org?genre=journal&eissn=1460-4787&date=1979 http://xlink.rsc.org?rft.genre=journal&rft.eissn=1460-4787&rft.date=1979 Biomaterials Science 2047-4849 http://dx.doi.org/10.1039/2047-4849/2013 http://xlink.rsc.org?genre=journal&issn=2047-4849&date=2013 http://xlink.rsc.org?rft.genre=journal&rft.issn=2047-4849&rft.date=2013 Catalysis Science & Technology 2044-4761 http://dx.doi.org/10.1039/2044-4761/2011 http://xlink.rsc.org?genre=journal&eissn=2044-4761&date=2011 -

Stahl Journal Abbreviations Masterlist
Please use a standard format for naming pdf files: YYJJ [Author's last name] [full or abbreviated title of article] YY = year of journal article; JJ = 2-4 letter abbreviation of journal name Full Journal Title Journal Abbrev. Stahl Abbrev. Accounts of Chemical Research Acc. Chem. Res. ACR ACS Applied Materials & Interfaces ACS Appl. Mater. Interfaces AMI ACS Catalysis ACS Catal. CAT ACS Central Science ACS Cent. Sci. CTS ACS Combinatorial Science ACS Comb. Chem. CBC ACS Energy Letters ACS Energy Lett. EL ACS Sustainable Chemistry & Engineering ACS Sustainable Chem. Eng. SCE ACS Omega ACS Omega AO ACS Medicinal Chemistry Letters ACS Med. Chem. Lett. MCL Acta Chemica Scandinavica Acta Chem. Scand. ACS Acta Crystallographica Section A: Foundations Acta Crystallogr., Sect. A: Found Chrstallogr. ACGA Acta Crystallographica Section B: Structural Science Acta Crystallogr., Sec. B: Struct. Sci ACGB Acta Crystallographica Section C: Chrstal Structure Communications Acta Crystallogr., Sec. C: Cryst. Struct. Commun. ACGC Acta Crystallographica Section D: Biological Crystallography Acta Crystallogr., Sec. D:Biol. Crystallogr. ACGD Acta Crystallographica Section E: Structure Reports Online Acta Crystallogr., Sec. E: Struct. Rep. Online ACGE Advanced Energy Materials Adv. Energy Mater. AEM Advanced Materials Adv. Mater AM Advanced Synthesis and Catalysis Adv. Synth. Catal. ASC Advances in Inorganic Chemistry Adv. Inorg. Chem AIC Analytical Chemistry Anal. Chem. ANC Angewandte Chemie Angew. Chem. AC Angewandte Chemie International Edition Angew. Chem., Int. Ed. ACIE Applied Catalysis A: General Appl. Catal., A ACA Applied Catalysis B: Environmental Appl. Catal.,B ACB Applied Energy Appl. Energy AE Australian Journal of Chemistry Aust. J. Chem. AJC Asian Journal of Organic Chemistry Asian. -
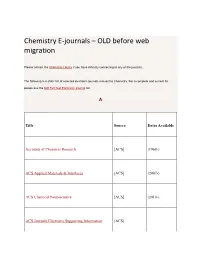
Chemistry E-Journals – OLD Before Web Migration
Chemistry E-journals – OLD before web migration Please contact the Chemistry Library if you have difficulty connecting to any of the journals. The following is a static list of selected electronic journals relevant to Chemistry. For a complete and current list please see the IUB Full Text Electronic Journal list. A Title Source Dates Available Accounts of Chemical Research [ACS] (1968-) ACS Applied Materials & Interfaces [ACS] (2007-) ACS Chemical Neuroscience [ACS] (2010-) ACS Journals Electronic Supporting Information [ACS] [Acta Chemica Acta Chemica Scandinavica (1947-1999) Scandinavica] Acta Crystallographica [IUCr] (1948-1967) Acta Crystallographica Section A: Foundations of [IUCr] (1968-) Crystallography Acta Crystallographica Section B: Structural Science [IUCr] (1968-) Acta Crystallographica Section C: Crystal Structure [IUCr] (1983-) Communications Acta Crystallographica Section D: Biological [IUCr] (1993-) Crystallography Acta Crystallographica Section E: Structure Reports [IUCr] Online (2001-) Advanced Functional Materials (continues Advanced [Wiley] Materials for Optics and Electronics) (2001-) Advanced Materials [Wiley] (1989-) Advanced Materials for Optics and Electronics (continued by Advanced Functional [Wiley] Materials) (1992-2000) Advanced Synthesis & Catalysis [Wiley] (1834-) Advances in Molecular Relaxation and Interaction [Elsevier Processes ScienceDirect] (1977-1982) Aldrichimica Acta [Sigma-Aldrich] (1968-) Amino Acids, Peptides and Proteins [RSC] (1998-2009) Analyst, The [RSC] (1876-) [Elsevier Analytica Chimica