Extended Null-Move Reductions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Regulations for the FIDE World Chess Cup 2017 2. Qualifying Events for World Cup 2017
Regulations for the FIDE World Chess Cup 2017 1. Organisation 1.1 The FIDE World Chess Cup (World Cup) is an integral part of the World Championship Cycle 2016-2018. 1.2 Governing Body: the World Chess Federation (FIDE). For the purpose of creating the regulations, communicating with the players and negotiating with the organisers, the FIDE President has nominated a committee, hereby called the FIDE Commission for World Championships and Olympiads (hereinafter referred to as WCOC) 1.3 FIDE, or its appointed commercial agency, retains all commercial and media rights of the World Chess Cup 2017, including internet rights. 1.4 Upon recommendation by the WCOC, the body responsible for any changes to these Regulations is the FIDE Presidential Board. 2. Qualifying Events for World Cup 2017 2. 1. National Chess Championships - National Chess Championships are the responsibility of the Federations who retain all rights in their internal competitions. 2. 2. Zonal Tournaments - Zonals can be organised by the Continents according to their regulations that have to be approved by the FIDE Presidential Board. 2. 3. Continental Chess Championships - The Continents, through their respective Boards and in co-operation with FIDE, shall organise Continental Chess Championships. The regulations for these events have to be approved by the FIDE Presidential Board nine months before they start if they are to be part of the qualification system of the World Chess Championship cycle. 2. 3. 1. FIDE shall guarantee a minimum grant of USD 92,000 towards the total prize fund for Continental Championships, divided among the following continents: 1. Americas 32,000 USD (minimum prize fund in total: 50,000 USD) 2. -

View 2020 Circular
2020 South African Junior Chess Championships 2020 Wild Card Chess Championship 2020 South Africa Junior Blitz Chess Championships 2020 South Africa Doubles Chess Championships 2020 Inter Regional Team Chess Championship 3 to 12 January 2021 Hosted by 4 Knights International Events Company CIRCULAR 1 Version 1.0 26 September 2020 Table of Contents 1. LOCAL ORGANIZING COMMITTEE (LOC) 5 1. CONVENER................................................................................................................................................. 5 2. TREASURER ................................................................................................................................................ 5 3. TECHNICAL DIRECTOR .................................................................................................................................. 5 4. CHIEF ARBITER ........................................................................................................................................... 5 5. ACCOMMODATION...................................................................................................................................... 5 6. MEDIA AND PHOTO’S .................................................................................................................................. 5 7. PUBLIC RELATIONS ...................................................................................................................................... 5 8. LOGISTICS ................................................................................................................................................. -

The Evects of Time Pressure on Chess Skill: an Investigation Into Fast and Slow Processes Underlying Expert Performance
Psychological Research (2007) 71:591–597 DOI 10.1007/s00426-006-0076-0 ORIGINAL ARTICLE The eVects of time pressure on chess skill: an investigation into fast and slow processes underlying expert performance Frenk van Harreveld · Eric-Jan Wagenmakers · Han L. J. van der Maas Received: 28 November 2005 / Accepted: 3 July 2006 / Published online: 22 December 2006 © Springer-Verlag 2006 Abstract The ability to play chess is generally Introduction assumed to depend on two types of processes: slow processes such as search, and fast processes such as One of the important challenges for cognitive science is pattern recognition. It has been argued that an increase to shed light on the processes that underlie expert in time pressure during a game selectively hinders the decision making. Across a wide range of Welds such as ability to engage in slow processes. Here we study the medical decision making and engineering, it has been eVect of time pressure on expert chess performance in shown that expertise involves both slow processes order to test the hypothesis that compared to weak such as selective search and fast processes such as the players, strong players depend relatively heavily on recognition of meaningful patterns (e.g., Ericsson & fast processes. In the Wrst study we examine the perfor- Staszewski 1989). This distinction between fast and slow mance of players of various strengths at an online chess processes is very applicable to the game of chess and server, for games played under diVerent time controls. therefore research on chess is of considerable impor- In a second study we examine the eVect of time con- tance for the understanding of expert performance. -

Chess Tests: Basic Suite, Positions 16-20
Chess Tests: Basic Suite, Positions 16-20 (c) Valentin Albillo, 2020 Last update: 14/01/98 See the Notes on Problem Solving 16.- Z. Franco vs. J. Gil FEN: rbb1N1k1/pp1n1ppp/8/2Pp4/3P4/4P3/P1Q2PPq/R1BR1K2/ b Black to play and win: 1. ... Nd7xc5 2. Qc5 Qh1+ 3. Ke2 Bg4+ 4. f3 Results Program CPU/Mhz Hash table Move Value Plys/Max Time Notes Chess Genius 1.0 P100 320 Kb Nd7xc5 +0.39 5/17 00:00:17 sees little value Chess Genius 1.0 P100 320 Kb Nd7xc5 +1.72 7/19 00:04:49 sees to 4. f3 Pentium Pro 200 MHz 24 Mb + 16 Mb Nd7xc5 +2.14 10/19 00:01:20 seen at 14s Crafty 12.6 P6 ? Nd7xc5 +1.181 11/17 00:01:46 see notes Crafty 13.3 Pentium Pro 200 Mhz ? Nd7xc5 +2.46 9 00:03:05 Chess Master 5500 Pentium Pro 200 Mhz 10 Mb Nd7xc5 +2.65 6 00:01:24 seen at 0:00, +0.00 MChess Pro 5.0 Notes: Using Chess Genius 1.0, both searches find the correct Knight's sacrifice. The 5-ply one, however, does not see it's full value, while the 7-ply search, though 16 times slower, correctly predicts the next 6 plies of the actual game, finding the move nearly two pawns worth. Crafty 12.6 finds the correct sacrifice too, though it needs to search to 10 ply, instead of the 7 plies required by CG1.0, but its better hardware makes for the shortest time. -

Learning Long-Term Chess Strategies from Databases
Mach Learn (2006) 63:329–340 DOI 10.1007/s10994-006-6747-7 TECHNICAL NOTE Learning long-term chess strategies from databases Aleksander Sadikov · Ivan Bratko Received: March 10, 2005 / Revised: December 14, 2005 / Accepted: December 21, 2005 / Published online: 28 March 2006 Springer Science + Business Media, LLC 2006 Abstract We propose an approach to the learning of long-term plans for playing chess endgames. We assume that a computer-generated database for an endgame is available, such as the king and rook vs. king, or king and queen vs. king and rook endgame. For each position in the endgame, the database gives the “value” of the position in terms of the minimum number of moves needed by the stronger side to win given that both sides play optimally. We propose a method for automatically dividing the endgame into stages characterised by different objectives of play. For each stage of such a game plan, a stage- specific evaluation function is induced, to be used by minimax search when playing the endgame. We aim at learning playing strategies that give good insight into the principles of playing specific endgames. Games played by these strategies should resemble human expert’s play in achieving goals and subgoals reliably, but not necessarily as quickly as possible. Keywords Machine learning . Computer chess . Long-term Strategy . Chess endgames . Chess databases 1. Introduction The standard approach used in chess playing programs relies on the minimax principle, efficiently implemented by alpha-beta algorithm, plus a heuristic evaluation function. This approach has proved to work particularly well in situations in which short-term tactics are prevalent, when evaluation function can easily recognise within the search horizon the con- sequences of good or bad moves. -
Draft – Not for Circulation
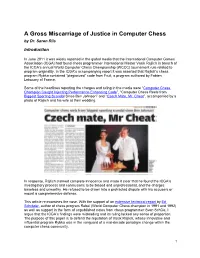
A Gross Miscarriage of Justice in Computer Chess by Dr. Søren Riis Introduction In June 2011 it was widely reported in the global media that the International Computer Games Association (ICGA) had found chess programmer International Master Vasik Rajlich in breach of the ICGA‟s annual World Computer Chess Championship (WCCC) tournament rule related to program originality. In the ICGA‟s accompanying report it was asserted that Rajlich‟s chess program Rybka contained “plagiarized” code from Fruit, a program authored by Fabien Letouzey of France. Some of the headlines reporting the charges and ruling in the media were “Computer Chess Champion Caught Injecting Performance-Enhancing Code”, “Computer Chess Reels from Biggest Sporting Scandal Since Ben Johnson” and “Czech Mate, Mr. Cheat”, accompanied by a photo of Rajlich and his wife at their wedding. In response, Rajlich claimed complete innocence and made it clear that he found the ICGA‟s investigatory process and conclusions to be biased and unprofessional, and the charges baseless and unworthy. He refused to be drawn into a protracted dispute with his accusers or mount a comprehensive defense. This article re-examines the case. With the support of an extensive technical report by Ed Schröder, author of chess program Rebel (World Computer Chess champion in 1991 and 1992) as well as support in the form of unpublished notes from chess programmer Sven Schüle, I argue that the ICGA‟s findings were misleading and its ruling lacked any sense of proportion. The purpose of this paper is to defend the reputation of Vasik Rajlich, whose innovative and influential program Rybka was in the vanguard of a mid-decade paradigm change within the computer chess community. -

Caissa Nieuws
rvd v CAISSA NIEUWS -,1. 374 Met een vraagtecken priJ"ken alleen die zetten, die <!-Cl'.1- logiSchcnloop der partij werkelijk ingrijpend vemol"en. Voor zichzelf·sprekende dreigingen zijn niet vermeld. · Ah, de klassieken ... april 1999 Caissanieuws 37 4 april 1999 Colofon Inhoud Redactioneel meer is, hij zegt toe uit de doeken te doen 4. Gerard analyseert de pijn. hoe je een eindspeldatabase genereert. CaïssaNieuws is het clubblad van de Wellicht is dat iets voor Ed en Leo, maar schaakvereniging Caïssa 6. Rikpareert Predrag. Dik opgericht 1-5-1951 6. Dennis komt met alle standen. verder ook voor elke Caïssaan die zijn of it is een nummer. Met een schaak haar spel wil verbeteren. Daar zijn we wel Clublokaal: Oranjehuis 8. Derde nipt naar zege. dik Van Ostadestraat 153 vrije avond en nog wat feestdagen in benieuwd naar. 10. Zesde langs afgrond. 1073 TKAmsterdam hetD vooruitzicht is dat wel prettig. Nog aan Tot slot een citaat uit de bespreking van Telefoon - clubavond: 679 55 59 dinsda_g_ 13. Maarten heeftnotatie-biljet op genamer is het te merken dat er mensen Robert Kikkert van een merkwaardig boek Voorzitter de rug. zijn die de moeite willen nemen een bij dat weliswaar de Grünfeld-verdediging als Frans Oranje drage aan het clubblad te leveren zonder onderwerp heeft, maar ogenschijnlijk ook Oudezijds Voorburgwal 109 C 15. Tuijl vloert Vloermans. 1012 EM Amsterdam 17. Johan ziet licht aan de horizon. dat daar om gevraagd is. Zo moet het! een ongebruikelijke visieop ons multi-culti Telefoon 020 627 70 17 18. Leo biedt opwarmertje. In deze aflevering van CN zet Gerard wereldje bevat en daarbij enpassant het we Wedstrijdleider interne com12etitie nauwgezet uiteen dat het beter kanen moet reldvoedselverdelingsvraagstukaan de orde Steven Kuypers 20. -

No. 123 - (Vol.VIH)
No. 123 - (Vol.VIH) January 1997 Editorial Board editors John Roycrqfttf New Way Road, London, England NW9 6PL Edvande Gevel Binnen de Veste 36, 3811 PH Amersfoort, The Netherlands Spotlight-column: J. Heck, Neuer Weg 110, D-47803 Krefeld, Germany Opinions-column: A. Pallier, La Mouziniere, 85190 La Genetouze, France Treasurer: J. de Boer, Zevenenderdrffi 40, 1251 RC Laren, The Netherlands EDITORIAL achievement, recorded only in a scientific journal, "The chess study is close to the chess game was not widely noticed. It was left to the dis- because both study and game obey the same coveries by Ken Thompson of Bell Laboratories rules." This has long been an argument used to in New Jersey, beginning in 1983, to put the boot persuade players to look at studies. Most players m. prefer studies to problems anyway, and readily Aside from a few upsets to endgame theory, the give the affinity with the game as the reason for set of 'total information' 5-raan endgame their preference. Your editor has fought a long databases that Thompson generated over the next battle to maintain the literal truth of that ar- decade demonstrated that several other endings gument. It was one of several motivations in might require well over 50 moves to win. These writing the final chapter of Test Tube Chess discoveries arrived an the scene too fast for FIDE (1972), in which the Laws are separated into to cope with by listing exceptions - which was the BMR (Board+Men+Rules) elements, and G first expedient. Then in 1991 Lewis Stiller and (Game) elements, with studies firmly identified Noam Elkies using a Connection Machine with the BMR realm and not in the G realm. -

The SSDF Chess Engine Rating List, 2019-02
The SSDF Chess Engine Rating List, 2019-02 Article Accepted Version The SSDF report Sandin, L. and Haworth, G. (2019) The SSDF Chess Engine Rating List, 2019-02. ICGA Journal, 41 (2). 113. ISSN 1389- 6911 doi: https://doi.org/10.3233/ICG-190107 Available at http://centaur.reading.ac.uk/82675/ It is advisable to refer to the publisher’s version if you intend to cite from the work. See Guidance on citing . Published version at: https://doi.org/10.3233/ICG-190085 To link to this article DOI: http://dx.doi.org/10.3233/ICG-190107 Publisher: The International Computer Games Association All outputs in CentAUR are protected by Intellectual Property Rights law, including copyright law. Copyright and IPR is retained by the creators or other copyright holders. Terms and conditions for use of this material are defined in the End User Agreement . www.reading.ac.uk/centaur CentAUR Central Archive at the University of Reading Reading’s research outputs online THE SSDF RATING LIST 2019-02-28 148673 games played by 377 computers Rating + - Games Won Oppo ------ --- --- ----- --- ---- 1 Stockfish 9 x64 1800X 3.6 GHz 3494 32 -30 642 74% 3308 2 Komodo 12.3 x64 1800X 3.6 GHz 3456 30 -28 640 68% 3321 3 Stockfish 9 x64 Q6600 2.4 GHz 3446 50 -48 200 57% 3396 4 Stockfish 8 x64 1800X 3.6 GHz 3432 26 -24 1059 77% 3217 5 Stockfish 8 x64 Q6600 2.4 GHz 3418 38 -35 440 72% 3251 6 Komodo 11.01 x64 1800X 3.6 GHz 3397 23 -22 1134 72% 3229 7 Deep Shredder 13 x64 1800X 3.6 GHz 3360 25 -24 830 66% 3246 8 Booot 6.3.1 x64 1800X 3.6 GHz 3352 29 -29 560 54% 3319 9 Komodo 9.1 -

Multilinear Algebra and Chess Endgames
Games of No Chance MSRI Publications Volume 29, 1996 Multilinear Algebra and Chess Endgames LEWIS STILLER Abstract. This article has three chief aims: (1) To show the wide utility of multilinear algebraic formalism for high-performance computing. (2) To describe an application of this formalism in the analysis of chess endgames, and results obtained thereby that would have been impossible to compute using earlier techniques, including a win requiring a record 243 moves. (3) To contribute to the study of the history of chess endgames, by focusing on the work of Friedrich Amelung (in particular his apparently lost analysis of certain six-piece endgames) and that of Theodor Molien, one of the founders of modern group representation theory and the first person to have systematically numerically analyzed a pawnless endgame. 1. Introduction Parallel and vector architectures can achieve high peak bandwidth, but it can be difficult for the programmer to design algorithms that exploit this bandwidth efficiently. Application performance can depend heavily on unique architecture features that complicate the design of portable code [Szymanski et al. 1994; Stone 1993]. The work reported here is part of a project to explore the extent to which the techniques of multilinear algebra can be used to simplify the design of high- performance parallel and vector algorithms [Johnson et al. 1991]. The approach is this: Define a set of fixed, structured matrices that encode architectural primitives • of the machine, in the sense that left-multiplication of a vector by this matrix is efficient on the target architecture. Formulate the application problem as a matrix multiplication. -

Rules & Regulations for the Candidates Tournament of the FIDE
Rules & regulations for the Candidates Tournament of the FIDE World Championship cycle 2016-2018 1. Organisation 1. 1 The Candidates Tournament to determine the challenger for the 2018 World Chess Championship Match shall be organised in the first quarter of 2018 and represents an integral part of the World Chess Championship regulations for the cycle 2016- 2018. Eight (8) players will participate in the Candidates Tournament and the winner qualifies for the World Chess Championship Match in the last quarter of 2018. 1. 2 Governing Body: the World Chess Federation (FIDE). For the purpose of creating the regulations, communicating with the players and negotiating with the organisers, the FIDE President has nominated a committee, hereby called the FIDE Commission for World Championships and Olympiads (hereinafter referred to as WCOC) 1. 3 FIDE, or its appointed commercial agency, retains all commercial and media rights of the Candidates Tournament, including internet rights. These rights can be transferred to the organiser upon agreement. 1. 4 Upon recommendation by the WCOC, the body responsible for any changes to these Regulations is the FIDE Presidential Board. 1. 5 At any time in the course of the application of these Regulations, any circumstances that are not covered or any unforeseen event shall be referred to the President of FIDE for final decision. 2. Qualification for the 2018 Candidates Tournament The players who qualify for the Candidates Tournament (excluding the World Champion who qualifies directly to the World Championship Match) are determined according to the following criteria, in order of priority: 2. 1 World Championship Match 2016 - The player who lost the 2016 World Championship Match qualifies. -

Super Human Chess Engine
SUPER HUMAN CHESS ENGINE FIDE Master / FIDE Trainer Charles Storey PGCE WORLD TOUR Young Masters Training Program SUPER HUMAN CHESS ENGINE Contents Contents .................................................................................................................................................. 1 INTRODUCTION ....................................................................................................................................... 2 Power Principles...................................................................................................................................... 4 Human Opening Book ............................................................................................................................. 5 ‘The Core’ Super Human Chess Engine 2020 ......................................................................................... 6 Acronym Algorthims that make The Storey Human Chess Engine ......................................................... 8 4Ps Prioritise Poorly Placed Pieces ................................................................................................... 10 CCTV Checks / Captures / Threats / Vulnerabilities ...................................................................... 11 CCTV 2.0 Checks / Checkmate Threats / Captures / Threats / Vulnerabilities ............................. 11 DAFiii Attack / Features / Initiative / I for tactics / Ideas (crazy) ................................................. 12 The Fruit Tree analysis process ............................................................................................................