Stagnation and Infall of Dense Clumps in the Stellar Wind of Τ Scorpii
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Apparent and Absolute Magnitudes of Stars: a Simple Formula
Available online at www.worldscientificnews.com WSN 96 (2018) 120-133 EISSN 2392-2192 Apparent and Absolute Magnitudes of Stars: A Simple Formula Dulli Chandra Agrawal Department of Farm Engineering, Institute of Agricultural Sciences, Banaras Hindu University, Varanasi - 221005, India E-mail address: [email protected] ABSTRACT An empirical formula for estimating the apparent and absolute magnitudes of stars in terms of the parameters radius, distance and temperature is proposed for the first time for the benefit of the students. This reproduces successfully not only the magnitudes of solo stars having spherical shape and uniform photosphere temperature but the corresponding Hertzsprung-Russell plot demonstrates the main sequence, giants, super-giants and white dwarf classification also. Keywords: Stars, apparent magnitude, absolute magnitude, empirical formula, Hertzsprung-Russell diagram 1. INTRODUCTION The visible brightness of a star is expressed in terms of its apparent magnitude [1] as well as absolute magnitude [2]; the absolute magnitude is in fact the apparent magnitude while it is observed from a distance of . The apparent magnitude of a celestial object having flux in the visible band is expressed as [1, 3, 4] ( ) (1) ( Received 14 March 2018; Accepted 31 March 2018; Date of Publication 01 April 2018 ) World Scientific News 96 (2018) 120-133 Here is the reference luminous flux per unit area in the same band such as that of star Vega having apparent magnitude almost zero. Here the flux is the magnitude of starlight the Earth intercepts in a direction normal to the incidence over an area of one square meter. The condition that the Earth intercepts in the direction normal to the incidence is normally fulfilled for stars which are far away from the Earth. -

Volume 75 Nos 3 & 4 April 2016 News Note
Volume 75 Nos 3 & 4 April 2016 In this issue: News Note – Galaxy alignment on a cosmic scale News Note – Presentation of EdinburghMedal Port Elizabeth Peoples’ Observatory Updated Biographical Index to MNASSA and JASSA EDITORIAL Mr Case Rijsdijk (Editor, MNASSA ) BOARD Mr Auke Slotegraaf (Editor, Sky Guide Africa South ) Mr Christian Hettlage (Webmaster) Prof M.W. Feast (Member, University of Cape Town) Prof B. Warner (Member, University of Cape Town) MNASSA Mr Case Rijsdijk (Editor, MNASSA ) PRODUCTION Dr Ian Glass (Assistant Editor) Ms Lia Labuschagne (Book Review Editor) Willie Koorts (Consultant) EDITORIAL MNASSA, PO Box 9, Observatory 7935, South Africa ADDRESSES Email: [email protected] Web page: http://mnassa.saao.ac.za MNASSA Download Page: www.mnassa.org.za SUBSCRIPTIONS MNASSA is available for free download on the Internet ADVERTISING Advertisements may be placed in MNASSA at the following rates per insertion: full page R400, half page R200, quarter page R100. Small advertisements R2 per word. Enquiries should be sent to the editor at [email protected] CONTRIBUTIONS MNASSA mainly serves the Southern African astronomical community. Articles may be submitted by members of this community or by those with strong connections. Else they should deal with matters of direct interest to the community . MNASSA is published on the first day of every second month and articles are due one month before the publication date. RECOGNITION Articles from MNASSA appear in the NASA/ADS data system. Cover picture: An image of the deep radio map covering the ELAIS-N1 region, with aligned galaxy jets. The image on the left has white circles around the aligned galaxies; the image on the right is without the circles. -

Stars and Their Spectra: an Introduction to the Spectral Sequence Second Edition James B
Cambridge University Press 978-0-521-89954-3 - Stars and Their Spectra: An Introduction to the Spectral Sequence Second Edition James B. Kaler Index More information Star index Stars are arranged by the Latin genitive of their constellation of residence, with other star names interspersed alphabetically. Within a constellation, Bayer Greek letters are given first, followed by Roman letters, Flamsteed numbers, variable stars arranged in traditional order (see Section 1.11), and then other names that take on genitive form. Stellar spectra are indicated by an asterisk. The best-known proper names have priority over their Greek-letter names. Spectra of the Sun and of nebulae are included as well. Abell 21 nucleus, see a Aurigae, see Capella Abell 78 nucleus, 327* ε Aurigae, 178, 186 Achernar, 9, 243, 264, 274 z Aurigae, 177, 186 Acrux, see Alpha Crucis Z Aurigae, 186, 269* Adhara, see Epsilon Canis Majoris AB Aurigae, 255 Albireo, 26 Alcor, 26, 177, 241, 243, 272* Barnard’s Star, 129–130, 131 Aldebaran, 9, 27, 80*, 163, 165 Betelgeuse, 2, 9, 16, 18, 20, 73, 74*, 79, Algol, 20, 26, 176–177, 271*, 333, 366 80*, 88, 104–105, 106*, 110*, 113, Altair, 9, 236, 241, 250 115, 118, 122, 187, 216, 264 a Andromedae, 273, 273* image of, 114 b Andromedae, 164 BDþ284211, 285* g Andromedae, 26 Bl 253* u Andromedae A, 218* a Boo¨tis, see Arcturus u Andromedae B, 109* g Boo¨tis, 243 Z Andromedae, 337 Z Boo¨tis, 185 Antares, 10, 73, 104–105, 113, 115, 118, l Boo¨tis, 254, 280, 314 122, 174* s Boo¨tis, 218* 53 Aquarii A, 195 53 Aquarii B, 195 T Camelopardalis, -

ANHANG Zahlenbeispiele Allgemeine Hinweise 1. in Den Folgenden
ANHANG I. TEIL Zahlenbeispiele Allgemeine Hinweise 1. In den folgenden Zahlenbeispielen wurde in mehreren Fallen unterstellt, da/3 die Zeitsignale der astronomischen Weltzeit UT 0 entsprechen, da die Be obachtungen teilweise vor der Beriicksichtigung der Unregelmi:i/3igkeiten der Erddrehung bei der Zeitfestlegung gemacht wurden, und/oder die Signalkorrek tionen bei der Auswertung nicht bekannt waren. Die Laufzeit der Signale vom Sender bis zum Empfi:inger wurde in diesen Fallen nicht beriicksichtigt. Auf eine nachtragliche Beriicksichtigung der Signalkorrektionen und der Laufzeit wurde verzichtet, da die Absolutwerte der Zeit-, Langen- und Azimutbestim mungen fiir das Handbuch eine untergeordnete Bedeutung haben, und Breiten bestimmungen dadurch nicht beeinflu/3t werden. Die strenge Ermittlung der W eltzeiten UT 2 und UT 0 durch Anschlu/3 der Beobachtungsuhr an Zeitsignale wird in Zahlenbeispiel 1 gezeigt. 2. Abkiirzungen: App. Pl. 64 = Apparent Places of Fundamental Stars 1964, AE 64 = The Astronomical Ephemeris 1964, Bull. Hor. = Bulletin Horaire, Serie J, BIR, Circulaire D = Bureau International de l'Heure, Circulaire D. 3. Die Herkunft der in den Zahlenbeispielen angegebenen Formeln wird durch die Nummern des Paragraphen und der Formel angegeben, z.B. § 14(3). 1. Ermittlung der Weltzeiten UT2 und UTO durch AnschluB der Beobachtungs uhr an Zeitsignale Die am 10. Juli 1968 auf der astronomischen Beobachtungsstation der Uni versiti:it Stuttgart (<pr:::: 48° 4 7', AE r:::; 9° 13') mit einem geni:ihert auf Weltzeit ein regulierten Druckchronographen registrierte Uhrzeit U = ist in die entsprechenden Weltzeiten U T2 und U TO umzurechnen. Die kurz zuvor durch den Anschlu/3 an den Sender DIZ Nauen, der die vom Geodi:itischen In- 702 ZAHLENBEISPIELE stitut Potsdam ermittelten Dauerzeitsignale ausstrahlt, ohne Beriicksichtigung der Laufzeit der elektromagnetischen Wellen bestimmte Uhrkorrektion betragt u = + OU49. -

Theory of Stellar Atmospheres
© Copyright, Princeton University Press. No part of this book may be distributed, posted, or reproduced in any form by digital or mechanical means without prior written permission of the publisher. EXTENDED BIBLIOGRAPHY References [1] D. Abbott. The terminal velocities of stellar winds from early{type stars. Astrophys. J., 225, 893, 1978. [2] D. Abbott. The theory of radiatively driven stellar winds. I. A physical interpretation. Astrophys. J., 242, 1183, 1980. [3] D. Abbott. The theory of radiatively driven stellar winds. II. The line acceleration. Astrophys. J., 259, 282, 1982. [4] D. Abbott. The theory of radiation driven stellar winds and the Wolf{ Rayet phenomenon. In de Loore and Willis [938], page 185. Astrophys. J., 259, 282, 1982. [5] D. Abbott. Current problems of line formation in early{type stars. In Beckman and Crivellari [358], page 279. [6] D. Abbott and P. Conti. Wolf{Rayet stars. Ann. Rev. Astr. Astrophys., 25, 113, 1987. [7] D. Abbott and D. Hummer. Photospheres of hot stars. I. Wind blan- keted model atmospheres. Astrophys. J., 294, 286, 1985. [8] D. Abbott and L. Lucy. Multiline transfer and the dynamics of stellar winds. Astrophys. J., 288, 679, 1985. [9] D. Abbott, C. Telesco, and S. Wolff. 2 to 20 micron observations of mass loss from early{type stars. Astrophys. J., 279, 225, 1984. [10] C. Abia, B. Rebolo, J. Beckman, and L. Crivellari. Abundances of light metals and N I in a sample of disc stars. Astr. Astrophys., 206, 100, 1988. [11] M. Abramowitz and I. Stegun. Handbook of Mathematical Functions. (Washington, DC: U.S. Government Printing Office), 1972. -

Modern Physics
REVIEWS OF MODERN PHYSICS VoLUME 29, NuMBER 4 OcroBER, 1957 Synthesis of the Elements in Stars* E. MARGARET BURBIDGE, G. R. BURBIDGE, WILLIAM: A. FOWLER, AND F. HOYLE Kellogg Radiation1Laboratory, California Institute of Technology, and M aunt Wilson and Palomar Observatories, Carnegie Institution of Washington, California Institute of Technology, Pasadena, California "It is the stars, The stars above us, govern our conditions"; (King Lear, Act IV, Scene 3) but perhaps "The fault, dear Brutus, is not in our stars, But in ourselves," (Julius Caesar, Act I, Scene 2) TABLE OF CONTENTS Page I. Introduction ...............................................................· ............... 548 A. Element Abundances and Nuclear Structure. 548 B. Four Theories of the Origin of the Elements ............................................... 550 C. General Features of Stellar Synthesis ..................................................... 550 II. Physical Processes Involved in Stellar Synthesis, Their Place of Occurrence, and the Time-Scales Associated with Them ...............· ..................... · ................................. 551 A. Modes of Element Synthesis ............................................................. 551 B. Method of Assignment of Isotopes among Processes (i) to (viii) .............................. 553 C. Abundances and Synthesis Assignments Given in the Appendix. 555 D. Time-Scales for Different Modes of Synthesis .............................................. 556 III. Hydrogen Burning, Helium Burning, the a Process, -

The Quantitative Chemical Analysis Ot Early-Type Stars
The Quantitative Chemical Analysis ot Early-type Stars LAWRENCE H. ALLER The Observatory, University of Michigan, Ann Arbor, Michigan, U.S.A. SUMMARY The University of Michigan programme for the determination of the abundances of the elements in hot stars involves an observational, a theoretical, and an experimental phase. A description of the spectrum of 7 Pegasi from •3570-).3970 and the profiles of the stronger lines in the photographic region illustrate the type of observational material that is being employed in this investigation. The point of view adopted for the theoretical programme is next described. Briefly, the model atmosphere of any given star must represent the observations of the continuous energy distribution, the Balmer discontinuity, the relative intensities of different spectral lines and the profiles of the stronger lines, notably those of hydrogen and helium. For this phase, a knowledge of the line-broadening coefficient is essential. Hence the emphasis on the experimental work with the luminous shock tube in which the Stark broadening of lines of hydrogen and other gases can be studied. 1. INTRODUCTION THE spectra of the stars of early spectral class present some of the most engaging problems in astrophysics. Studies of stellar associations, such as the Lacerta aggregate, make it appear extremely likely that these stars are continuously being formed from the interstellar medium in the spiral arms of our galaxy (BLAAUW, 1952). The compositions of their atmospheres should reflect that of the interstellar medium, at least for young stars or for objects in which no mixing takes place between the atmosphere and interior. -

The Sidereal Times
Observe—Educate—Have Fun September 2018 The Sidereal Times The Official Newsletter of The Albuquerque Astronomical Society P.O. Box 50581, Albuquerque, New Mexico 87181-0581 www.TAAS.org taas — 2011 winner of astronomy magazine’s out-of-this-world award for outstanding public programming since 1959 General Meeting News Lynne Olson The Next Step You have completed all four of Phil Fleming’s Fabulous 50 sessions and you now have a familiarity with where some of the prominent objects are in the sky. Con- gratulations! Phil has taught you about items like plani- spheres and sky charts. So, what is next? Now it is time to use your telescope to find objects that you cannot see with the naked eye. Armed with a telescope, planisphere, sky charts, and/or a planetarium program you are ready to do some star hopping and to take The Next Step. TAAS GenerAl MeeTinG TAAS ASTrOnOMY 101 “Let There Be Light” “Filters for Viewing Deep-Sky Objects” The concept for The Next Step is to meet Howard J. Brewington Martin Hilario at GNTO during a New Moon Observing Saturday, September 29, 7:00pm Saturday, September 29, 6:00pm session and find a number of Deep-Space UnM Science and Math UnM Science and Math Objects that I will announce on TAAS_Talk learning Center* learning Center* a week or so before the session. I will as- Free and Open to the Public Free and Open to the Public sist you in using your equipment to find the objects. • Howard J. Brewington is the speaker for TAAS vice president Martin Hilario will What you need to do to participate: be the speaker for Astronomy 101, at 6 p.m. -

Constellations
Your Guide to the CONSTELLATIONS INSTRUCTOR'S HANDBOOK Lowell L. Koontz 2002 ii Preface We Earthlings are far more aware of the surroundings at our feet than we are in the heavens above. The study of observational astronomy and locating someone who has expertise in this field has become a rare find. The ancient civilizations had a keen interest in their skies and used the heavens as a navigational tool and as a form of entertainment associating mythology and stories about the constellations. Constellations were derived from mankind's attempt to bring order to the chaos of stars above them. They also realized the celestial objects of the night sky were beyond the control of mankind and associated the heavens with religion. Observational astronomy and familiarity with the night sky today is limited for the following reasons: • Many people live in cities and metropolitan areas have become so well illuminated that light pollution has become a real problem in observing the night sky. • Typical city lighting prevents one from seeing stars that are of fourth, fifth, sixth magnitude thus only a couple hundred stars will be seen. • Under dark skies this number may be as high as 2,500 stars and many of these dim stars helped form the patterns of the constellations. • Light pollution is accountable for reducing the appeal of the night sky and loss of interest by many young people as the night sky is seldom seen in its full splendor. • People spend less time outside than in the past, particularly at night. • Our culture has developed such a profusion of electronic devices that we find less time to do other endeavors in the great outdoors. -
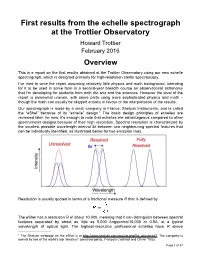
First Results from the Echelle Spectrograph at the Trottier Observatory Howard Trottier February 2016 Overview
First results from the echelle spectrograph at the Trottier Observatory Howard Trottier February 2016 Overview This is a report on the first results obtained at the Trottier Observatory using our new echelle spectrograph, which is designed primarily for high-resolution stellar spectroscopy. I’ve tried to write the report assuming relatively little physics and math background, intending for it to be used in some form in a second-year breadth course on observational astronomy that I’m developing for students from both the arts and the sciences. However the level of the report is somewhat uneven, with some parts using more sophisticated physics and math – though the math can usually be skipped entirely in favour of the interpretation of the results. Our spectrograph is made by a small company in France, Shelyak Instruments, and is called the “eShel” because of its “echelle” design.1 The basic design principles of echelles are reviewed later; for now, it’s enough to note that echelles are advantageous compared to other spectrometer designs because of their high resolution. Spectral resolution is characterized by the smallest possible wavelength interval δλ between two neighbouring spectral features that can be individually identified, as illustrated below for two emission lines. # Resolution is usually quoted in terms of a fractional measure R that is defined by # The eShel has a resolution R of about 10,000, meaning that it can distinguish between spectral features separated by about as little as 5,000 Angstroms/10,000 or 0.5Å, at a typical wavelength of optical light. The highest-resolution professional echelles have R above 1 The Shelyak webpage on the eShel is at http://www.shelyak.com/dossier.php?id_dossier=47. -

Stagnation and Infall of Dense Clumps in the Stellar Wind of Tau Scorpii
Stagnation and Infall of Dense Clumps in the Stellar Wind of τ Scorpii J. Christopher Howk1, Joseph P. Cassinelli University of Wisconsin-Madison Department of Astronomy Jon E. Bjorkman University of Toledo Dept. of Physics & Astronomy and Henny J.G.L.M. Lamers University of Utrecht Astronomical Institute ABSTRACT Observations of the B0.2 V star τ Scorpii have revealed unusual stellar wind characteristics: red-shifted absorption in the far-ultraviolet O VI resonance doublet up to +250 km s−1, and ∼ extremely hard X-ray emission implying gas at temperatures in excess of 107 K. We describe a phenomenological model to explain these properties. We assume the wind of τ Sco consists of two components: ambient gas in which denser clumps are embedded. The clumps are optically thick in the UV resonance lines primarily responsible for accelerating the ambient wind. The reduced acceleration causes the clumps to slow and even infall, all the while being confined by the ram pressure of the outflowing ambient wind. We calculate detailed trajectories of the clumps in the ambient stellar wind, accounting for a line radiation driving force and the momentum deposited by the ambient wind in the form of drag. We show these clumps will fall back towards the star with velocities of several hundred km s−1 for a broad range of initial conditions. The velocities of the clumps relative to the ambient stellar wind can approach 2000 km s−1, producing X-ray emitting plasmas with temperatures in excess of (1 6) 107 K in bow − × shocks at their leading edge. -
Notes Stars - Huge Bright Balls of Gas Fueled by Nuclear Energy Stars Energy Source
STARS Notes Stars - Huge bright balls of gas fueled by nuclear energy Stars Energy Source • Nuclear Energy • Nuclear Fusion of mainly Hydrogen into Helium atoms. • Gives off electromagnetic radiation. – Light, heat and other forms of energy Stars Nuclear Energy The Sun – Our Star The closest star to Earth • Medium size • Yellow • Main Sequence Star • 150,000,000 Km (93 Million miles) away. • 4.5 - 5 billion years old • Will last about another 5 billion years • Located near the edge of our disc shaped galaxy – The Milky Way Stars are very far away • The Sun is the closest star to Earth – 150,000,000 km away • The next closest star is Proxima Centauri – 39,900,000,000,000 km away – 4.2 light years • The Sun • Stars are extremely far away!!! • The Sun is thousands of times closer to Earth than other stars • Proxima Centauri Stars are classified by surface temperature - color Class Color Surface Temp. Elements Examples of (degrees Celsius) detected stars O Blue Above 30,000 Helium 10 Lacertae Blue-white 10,000 - 30,000 Helium and Rigel, Spica B Hydrogen A Blue-white 7,500 - 10,000 Hydrogen Vega, Sirius Yellow- 6,000 - 7,500 Hydrogen and Canopus, F white heavier Procyon elements Yellow 5,000 - 6,000 Calcium and The sun, G other metals Capella Orange 3,500 - 5,000 Calcium and Arcturus, K Molecules Aldebaran Red Less than 5,000 Molecules Betelgeuse, M Antares Hertzprung–Russel (H-R) Diagram - a graph that shows the relationship between a star’s surface temperature and it’s brightness (absolute magnitude/Luminosity).