Redalyc.Understanding the Arithmetic of Color
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
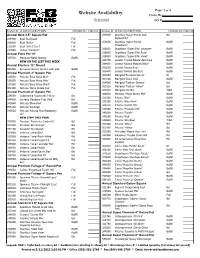
Website Availability Order By: 5/11/2013 PO
Page: 1 of 4 Website Availability Order By: 5/11/2013 PO #: Product # ITEM DESCRIPTION COMMENT ORDER Product # ITEM DESCRIPTION COMMENT ORDER Annual Herb 3.5" Square Pot 259550 Dianthus 'Super Parfait Red Bd 209400 Basil 'Boxwood' Full Peppermint' 209660 Basil 'Nufar' Full 259650 Dianthus 'Super Parfait Bd/Bl Strawberry' 210500 Basil 'Sweet Dani' Full 285850 Impatiens 'Super Elfin Lavender' Bd/Bl 237950 Chives 'Common' Full Annual Patio Pot 10" 286600 Impatiens 'Super Elfin Rose' Bd/Bl 286950 Impatiens 'Super Elfin Violet' Bd/Bl 305710 Marigold 'Narai Orange' Bd/Bl 298750 Lobelia 'Crystal Palace' dark blue Bd/Bl NEW ON THE LIST THIS WEEK Annual Planters 12" Round 299950 Lobelia 'Riviera Midnight Blue' Bd/Bl 300250 Lobelia 'Riviera Rose' Bd/Bl 954400 European Basket Garden with pick Bd/Bl 300400 Lobelia 'Riviera Sky Blue' Bd/Bl Annual Premium 2" Square Pot 303850 Marigold 'Bonanza Yellow' Bl 335850 Petunia 'Easy Wave Blue' Full 304200 Marigold 'Disco Red' Bd/Bl 336650 Petunia 'Easy Wave Pink' Full 304900 Marigold 'Taishan Orange' Bd 337260 Petunia 'Easy Wave Violet' Full 305150 Marigold 'Taishan Yellow' Bd 351350 Petunia 'Wave Purple imp' Full 305410 Marigold 'Vanilla' Ttbd Annual Premium 4" Square Pot 306850 Mimulus 'Magic Blotch Mix' Bd/Bl 236550 Calibrachoa 'Superbells Yellow' Bd 331800 Petunia 'Blue' Bd/Bl 294600 Lantana 'Bandana Trail Gold' Bd 331900 Petunia 'Blue Morn' Bd/Bl 345690 Petunia 'Glow Red' Bd/Bl 339250 Petunia 'Patriot Mix' Bd/Bl 955180 Petunia 'Pinstripe' Bd/Bl 339500 Petunia 'Picobella Mix' Bd/Bl 345520 Petunia 'Potunia -

Swatch Name HLS RGB HEX Absolute Zero 217° 36% 100% 0 72
Swatch Name HLS RGB HEX Absolute Zero 217° 36% 100% 0 72 186 #0048BA Acid green 65° 43% 76% 176 191 26 #B0BF1A Aero 206° 70% 70% 124 185 232 #7CB9E8 Aero blue 151° 89% 100% 201 255 229 #C9FFE5 African violet 288° 63% 31% 178 132 190 #B284BE Air superiority blue 205° 60% 39% 114 160 193 #72A0C1 Alabaster 46° 90% 27% 237 234 224 #EDEAE0 Alice blue 208° 97% 100% 240 248 255 #F0F8FF Alloy orange 27° 42% 85% 196 98 16 #C46210 Almond 30° 87% 52% 239 222 205 #EFDECD Amaranth 348° 53% 78% 229 43 80 #E52B50 Amaranth (M&P) 328° 40% 57% 159 43 104 #9F2B68 Amaranth pink 338° 78% 75% 241 156 187 #F19CBB Amaranth purple 342° 41% 63% 171 39 79 #AB274F Amaranth red 356° 48% 73% 211 33 45 #D3212D Amazon 147° 35% 35% 59 122 87 #3B7A57 Amber 45° 50% 100% 255 191 0 #FFBF00 Amber (SAE/ECE) 30° 50% 100% 255 126 0 #FF7E00 Amethyst 270° 60% 50% 153 102 204 #9966CC Android green 74° 50% 55% 164 198 57 #A4C639 Antique brass 22° 63% 47% 205 149 117 #CD9575 Antique bronze 52° 26% 55% 102 93 30 #665D1E Antique fuchsia 316° 46% 22% 145 92 131 #915C83 Antique ruby 350° 31% 66% 132 27 45 #841B2D Antique white 34° 91% 78% 250 235 215 #FAEBD7 Ao (English) 120° 25% 100% 0 128 0 #008000 Apple green 74° 36% 100% 141 182 0 #8DB600 Apricot 24° 84% 90% 251 206 177 #FBCEB1 Aqua 180° 50% 100% 0 255 255 #00FFFF Aquamarine 160° 75% 100% 127 255 212 #7FFFD4 Swatch Name HLS RGB HEX Arctic lime 72° 54% 100% 208 255 20 #D0FF14 Army green 69° 23% 44% 75 83 32 #4B5320 Artichoke 76° 53% 13% 143 151 121 #8F9779 Arylide yellow 51° 67% 74% 233 214 107 #E9D66B Ash gray 135° 72% 8% 178 190 -

The Named Colors List Contains Over 1.500 Color Names with HEX and RGB Values, from "Absolute Zero" to "Zomp"
The Named Colors list contains over 1.500 color names with HEX and RGB values, from "Absolute Zero" to "Zomp". Color Preview Color Name Hex RGB Absolute Zero 0048BA 0, 72, 186 Acid green B0BF1A 176, 191, 26 Aero 7CB9E8 124, 185, 232 Aero blue C9FFE5 201, 255, 229 African violet B284BE 178, 132, 190 Air superiority blue 72A0C1 114, 160, 193 Alabama crimson AF002A 175, 0, 42 Alabaster F2F0E6 242, 240, 230 Aliceblue F0F8FF 240, 248, 255 Alloy orange C46210 196, 98, 16 Almond EFDECD 239, 222, 205 Aloeswood brown (Tonocha) 5A6457 90, 100, 87 Aloewood-color (Kyara-iro) 6A432D 106, 67, 45 Amaranth E52B50 229, 43, 80 Amaranth deep purple 9F2B68 159, 43, 104 Amaranth pink F19CBB 241, 156, 187 Amaranth purple AB274F 171, 39, 79 Amaranth red D3212D 211, 33, 45 Amazon 3B7A57 59, 122, 87 Amber FFBF00 255, 191, 0 Amber (Kohaku-iro) CA6924 202, 105, 36 Amber (SAE/ECE) FF7E00 255, 126, 0 Amethyst 9966CC 153, 102, 204 Amur cork tree (Kihada) F3C13A 243, 193, 58 Anti-flash white F2F3F4 242, 243, 244 Antique brass CD9575 205, 149, 117 Antique bronze 665D1E 102, 93, 30 Antique fuchsia 915C83 145, 92, 131 Color Preview ACnotlioqru eN arumbey H8e4x1B2D R1G32B, 27, 45 Antiquewhite FAEBD7 250, 235, 215 Apple 66B447 102, 180, 71 Apple green 8DB600 141, 182, 0 Apricot FBCEB1 251, 206, 177 Aqua 00FFFF 0, 255, 255 Aqua Blue color (Mizu-iro) 86ABA5 134, 171, 165 Aquamarine 7FFFD4 127, 255, 212 Arctic lime D0FF14 208, 255, 20 Army green 4B5320 75, 83, 32 Artichoke 8F9779 143, 151, 121 Arylide yellow E9D66B 233, 214, 107 Ash gray B2BEB5 178, 190, 181 Asparagus 87A96B -
Mexican Pink: Color Identity for a Nation
Секция 4 – 2D и 3D‐графика, графический дизайн, управление цветом MEXICAN PINK: COLOR IDENTITY FOR A NATION Tirtha Prasad Mukhopadhyay, Ph.D., professor of the department of Art, University of Guanajuato, Mexico Natalia Gurieva, Ph.D., professor of the department of Art, University of Guanajuato, Mexico Preciado Lopez Maria Fernanda student of the Digital Arts, University of Guanajuato, Mexico Mexican people are renown ed all over the world for their spontaneousness and charismatic culture, which also give them their charming and vivacious identity as individuals: the color rosa Mexicano or Mexican Pink forms a part of that cultural identity. We are investigating the origin of this color and would like to prove that the term indeed represents a color that has long been embedded in indigenous traditions and later Mestizo manifests, although it appears that this color did not have a name in Spanish before the last century. The word rosa comes from Spanish, and is of Latin origin; it designates both the color and the flower “rose”. In Mexico however the Spanish word rosa seems to have acquired additional meaning and therefore represent a red-purple color which is technically both bright and saturated. Mexican pink has been associated with the bugambilia flower color, an ornamental climbing plant. The original reference are the colors or pigment variants used in typical garments and others objects, like artifacts or basketry, of the traditional Mexican culture. Mexican pink began to be known after 1950 - thanks to fashion designer Ramón Valdiosera. In the middle of 1940, Valdiosera made a long research trip around Mexico where he contacted people from different ethnicities and collected characteristic clothes and typical garments of the different regions. -
Didn't Take Lunch T(Won
The Public Doesn't Care Bow a Newsp JSf ft Only Gets It and PRINtS It FIRST i-- ip , w Fircii A si ri:i nA JH Paso Morning Times g el onico Ml I l. H4RRKTH. periódico diario que llega a todo Suroeste el mismo día on Qué es publi- copper - aásTMeuaw cado, ciando fiel a su fecha cada día SHrer, per pa , .Vi del fio. lie La pagina ocho contiene las 1W ultimas noticias del día en español. 1I, ler ll .........!..!3.At4.nS Klnr, per WO lbs t ..... .. WXO&SO 34TR YfcAR. EL PASO. TEXAS . WEPftpPÁY, MARCH 25. 1914. TWELVE PAGES PRICE 5 CENTS VILLA AND BENAV DIDN'T TAKE LUNCH T(WON being her visit to a gunsmith to buy a revolver. an obviously hostile criticism of the M. Boucard Interrupted her to ask ir at throne in the memory of the oldest WOMAN TELLS that moment site planned her act or vio- ARISTOCRATS member nor even in the laat ceatury. lence against M. Calmette. Would the opposition members, he "Not .entirely ,". replied Mme. Calllaux. naked, be content to sit quietly and "The Idea then Only began to take root." permit him to preach sucH doctrines? AWAY Mme. Calllaux said he bad purchased a ME STILL OF SHOOTING revolver arier refusing one the trigger or London NetvsmMr Comment. Hfl which worked too hard, for protection on IN THE MUTINY By the Anoeiated irr nights in the country during the electoral London. MaYeh;25. The Unionist campaign or her husband, whom she In- morning papers fully admit that It HMrl. -

Rosa Mexicano: the Social Optics of a Colour Neologism
Journal of the International Colour Association (2017): 20, 12-27 Mukhopadhyay et al. Rosa mexicano: the social optics of a colour neologism Tirtha Prasad Mukhopadhyay1, Baidya Nath Saha2, Natalia Gurieva1 and Reynaldo Thompson Lopez1 1Department of Art and Enterprise, Universidad de Guanajuato, Mexico 2Centro de Investigación en Matemáticas (CIMAT), A. C. Monterrey, Mexico Emails: [email protected]; [email protected]; [email protected]; [email protected] The phrase ‘rosa mexicano’ or what is now called ‘Mexican Pink’ in English, began to be used in Mexico in the 1950s and has now been adopted as a representative colour for the Mexican nation state. A government agency like the CPTM (Consejo de Promoción Turística de México), or ‘The Council of Promotion of Tourism’, and the urban planning and administration unit of Mexico City, called by the acronym CDMX (Ciudad de Mexico), validates the phrase as a symbolic colour-name of the state and the culture of its peoples. The CPTM also endorses the Pantone Matching System colour ‘magenta’ #E50087 as this specific memorable colour, now called rosa mexicano or “Mexican Pink” as the appropriate colour of the ‘ancient Mexican peoples’. But despite such institutional and public endorsement, could we safely say that the term has indeed, gradually or otherwise, come to represent a semantic marker for the experience of a very geographically local variant of pink. Here we examine if the phrase rosa mexicano, or ‘Mexican Pink’ can be accepted as a true symbol of a long existing, recognisable colour and its visible social preference for people in Central America and Mexico in particular. -

Vegetable Varieties
Lee County 310 South Grimes Giddings, TX 78942 979-542-2753 Recommended Vegetable Varieties for Lee County Asparagus: UC157, UC 72, Jersey Giant, Jersey Gem Eggplant: Black Beauty, Ichibon, Florida Market, Florida High Bush, Tycoon (oriental) Bean, snap: Contender, Tendercrop, Top Crop, Blue Lake 274, Strike, Lake Superior Garlic: Elephant, Mexican Pink, Texas White Bean, pinto: UI-114, Olathe, Pindak, Dwarf Horticultural Kale: Dwarf Scotch, Vates Beet: Detroit Dark Red, Ruby Queen, Pacemaker Kohlrabi: White Vienna, Grand Duke Broccoli: Green Comet, Southern Comet, Galaxy, Premium Leek: American Flag, Titan Crop, Baccus, Early Dawn Lettuce, crisp head: Great Lakes 659 MT, Mission Cabbage: Market Prize, Rio Verde, Ruby Ball, Bravo, Solid Blue 760 Lettuce, leaf: Buttercrunch, Prizehead, Red Sails, Butterhead Cabbage, Chinese: Jade Pagoda, Monument, Napa Lettuce, romaine: Valmaine, Paris Island Cantaloupe: Ambrosia, Magnum 45, Mission, Perlita, TAM Mustard: Large Smoothleaf, Greenwave, Tendergreen Uvalde, Dixie Jumbo, Caravelle Okra: Clemson Spineless, Emerald, Lee, Velvet Carrot: Imperator 58, Nantes, Orlando Gold, TAM Gold Spike, Little Finger, Thumbelina Onion, short day: Texas 1015-Y, Early Grano 502, Granex Cauliflower: Snow Crown, Snowball Y Improved, Imperial 10 Onion, intermediate: Spano, Cimmaron, Midstar -6 Onion, long day: Armado, Durango, Valdez Celery: Utah 52-70, Summer or Giant Pascal, Florida 683 Parlsey: Moss Curled, Banquet Chives: Chinese, Garlic Peas, edible pod: Dwarf Gray Sugar, Sugar Snap Collards: Georgia Southern, -

Understanding the Arithmetic of Color
EDUCATION Revista Mexicana de F´ısica 61 (2015) 28–30 JANUARY–JUNE 2015 Understanding the arithmetic of color J. Medina Marquez´ a;¤, S.E. Balderas-Matab, and C. Zu´niga˜ Islasa aInstituto Nacional de Astrof´ısica, Optica´ y Electronica,´ Luis Enrique Erro No. 1 Sta. Ma. Tonantzintla, Puebla, 72840 Pue. Mexico.´ e-mail: [email protected]; [email protected] bUniversidad de Guadalajara, CUCEI, Departamento de Electronica,´ Blvd. Marcelino Garc´ıa Barragan´ # 1421, Guadalajara, Jalisco, Mexico,´ 44430, e-mail: [email protected] Received 13 January 2015; accepted 26 January 2015 In this work we propose to introduce Arithmetic for the Mixture of Colors, which can be defined from dividing the electromagnetic spectrum of white light in three thirds, and by associating each of them to an algebraic expression of the three primary additive and subtractive colors. Then, we will give the rules for adding or subtracting to predict the new mixture of resultant colors. Keywords: Mixture of colors; chromatic arithmetic. PACS: 01.40.E, 01.40.eg, 01.40ek 1. Introduction there is an overlap of these emitted lights. The repre- sentation of this mixture will be represented with the If we ask randomly to any person on the street how much is plus sign (+). three plus two, probably, we will get the answer without any problem. If, instead of asking them to sum these two num- ² In this sense, the additive mixture of the three thirds of bers, we ask them to subtract them, practically any person the rainbow forms again the original white light, which would answer that the result is one. -

Koh-I-Noor Polycolor Comparison Addendum
is addendum chart was created to help colorists with older (and newer) Polycolor sets chart their pencils. Koh-I-Noor has had many di erent sets available over the years (12, 24, 36, 48, and 72) plus a few di erent themed collections such as the 24 landscape set and portrait sets. To help alleviate some confusion, this chart contains all of the colors including several that have since been discontinued. Colors marked with ** were included in the original set of 72 colors, but are not included the set of 144 newer colors (discontinued). Also, several color names have changed, so both (where applicable) are indicated in the chart: new color name / old color name. 558 Fire Orange 650 Fig Purple 126 Persian Orange / Dark Orange 131 French Pink / Pink 5 Reddish Orange / Orange 653 Mexican Pink 1 Titanium White / White 350 Portrait Peach 353 Amaranth Pink 500 Ivory Bone 559 Portland Orange 651 Orchid Purple 2 Light Yellow ** 560 Dark Salmon Orange 177 Lilac Violet / Light Violet 501 Pollen Yellow 6 Vermilion Red / Red 655 Byzantium Purple 41 Banana Yellow / Cream 48 Carmine Red ** 178 Reddish Violet / Red Violet 3 Chrome Yellow / Yellow 600 Light Scarlet Red 654 Dark Reddish Violet 4 Dark Yellow ** 601 Scarlet Red (was 47) 182 Dark Violet / Delft Blue 502 Lime Yellow 170 Pyrrole Red / Carmine 180 Dark Lavender Violet / Windsor 503 Chartreuse Yellow 604 Coral Red 13 Lavender Violet / Violet 504 Lemon Yellow 610 Light Carmine Red 179 Bluish Violet / Permanent Violet 43 Canary Yellow ** 609 Antique Rose 181 Windsor Violet / Blue Violet 9 Beige -

In Colour Emotive Architecture
Emotive in architecture colour Luis Barragán Chloé Eersel Delft University of Technology January 2016 Abstract Colour is a very powerful design tool that is not often used by architects. Most buildings around us have very monochrome or neutral palettes. With colour emotions can be evoked and architects could have an impact on people’s lives. An architect that dared to use bold colours in his emotive architecture was Luis Barragán. In his architecture, colour was one of the fundamental components. The theories of Johannes Itten and Wassily Kandinksy show that determining how colour is perceived is a very complex issue. Colours are perceived through different psychological layers making colour-emotion association different for everyone. Using symbolic, expressive and impressive effects of colour, three projects of Luis Barragán are analysed on the topic of how these colour effects can help evoke emotion in the built environment. In the Chapel de las Madres Capuchinas, the symbolic use of colour can be seen. The impressive effect of colour can be seen in Los Clubes. Casa Gilardi shows a sequence of different harmonies playing with the different expressions of colour. Impressive colour use is found to be the most universal as it relies on the biology of humans. Symbolic use of colour is already more specific and its perception depends mainly on culture. Expressive colour use is based on personal preference and is different for everyone. Keywords: colour psychology, Luis Barragán, emotive architecture, colour theory, colour perception, colour-emotion asscoiation iii Table of contents Abstract iii List of figures v 1. Introduction 1 1.1 Omission of colour 1 1.2 Colour and emotion 1 1.3 Luis Barragán 2 1.4 The three problems of colour 2 2. -

Agency and Materiality in Barragán's Casa Estudio Patricia Pérez Rabelo
Collaborative Matter: Agency and Materiality in Barragán's Casa Estudio Patricia Pérez Rabelo A Thesis in the Department of Art History Presented in Partial Fulfillment of the Requirements for the Degree of Master of Arts (Art History) Concordia University Montréal, Québec, Canada March 2021 © Patricia Pérez Rabelo, 2021 CONCORDIA UNIVERSITY School of Graduate Studies This is to certify that the thesis prepared By: Patricia Pérez Rabelo Entitled: Collaborative Matter: Agency and Materiality in Barragán!s Casa Studio. and submitted in partial fulfillment of the requirements for the degree of Master of Arts (Art History) complies with the regulations of the University and meets the accepted standards with respect to originality and quality. Signed by the final examining committee: ______________________________________ Examiner Dr. Kristina Huneault ____________________________________ Thesis Supervisor Dr. Nicola Tullio Pezolet Approved by _______________________________________ Dr. Johanne Sloan, Chair _______ 2021 _______________________________________ Dr. Annie Gérin, Dean of Faculty of Fine Arts iii Abstract Collaborative Matter: Agency and Materiality in Barragán's Casa Estudio Patricia Pérez Rabelo Although materials are well-understood as a central component in a building's construction, they seldom are discussed as collaborators in that construction. Instead, they take the place of the raw and inert matter through which the architect expresses their vision. To better situate materials as collaborators, this thesis focuses on Casa Estudio Luis Barragán, the home and studio of late Mexican architect Luis Ramiro Barragán Morfín (1902-1988), to investigate how particular ma- terials are active participants in the process of construction. My argument follows a New Materi- alist framework that allows me to focus in-depth on some of the relationships between materials, people, and plants that comprise Casa Estudio. -

Specialty Florist Liners 2016
SSPECIALTYPECIALTY FFLORISTLORIST LLINERSINERS 22016016 New Varieties Gerbera Bengal series Mix, Orange, Orange w/ Eye, Red w/ Eye, Rose w/ Eye, White, Yellow w/ Eye The new Bengal series is the big brother to the Jaguar series with a bigger, more vigorous plant habit. Large fl owers are uniformly sized across the series with strong, sturdy stems. Well-suited to 5-6” pots. Finish pots from our 72s in 9-10 weeks. (144, 72) Gerbera Flori Line Midi Pink Splash Mix Slightly more compact with slightly smaller fl owers than Maxi types, the Flori Line Midi series offers a shorter crop time with a nice selection of novelty and traditional colors. The new Pink Splash Mix is a bright mix perfect for Valentine’s Day or Mother’s Day. Finish in 4-5” pots from our 72s in 8-9 weeks. (144, 72) Pictured on next page. BBengalengal OOrangerange D BBengalengal OOrangerange ww// EEyeye D BBengalengal RReded ww// EEyeye D BBengalengal RRoseose w/w/ EEyeye D BBengalengal WWhitehite D BBengalengal YYellowellow ww// EEyeye D Substitution List Item no longer listed: Available Sub: Item no longer listed: Available Sub: Gerbera Cartwheel Chardonnay No Sub, Custom Sow Available Gerbera FL Mini Dark Eye Contour No Sub, Custom Sow Available Gerbera FL Maxi Dark Eye EC Purple FL Midi Dark Eye EC Purple Gerbera FL Mini Dark Eye EC Hot Pink No Sub, Custom Sow Available Gerbera FL Maxi Dark Eye Fireball FL Midi Dark Eye Dark Fireball Gerbera FL Mini Dark Eye EC Red No Sub, Custom Sow Available Gerbera FL Maxi Dark Eye Orange FL Midi Dark Eye Orange Gerbera Jaguar Orange Picotee