Gnowee: a Hybrid Metaheuristic Optimization Algorithm For
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Imaging White Blood Cells Using a Snapshot Hyper-Spectral Imaging System
Graduate Theses, Dissertations, and Problem Reports 2016 Imaging White Blood Cells using a Snapshot Hyper-Spectral Imaging System Christopher John Robison Follow this and additional works at: https://researchrepository.wvu.edu/etd Recommended Citation Robison, Christopher John, "Imaging White Blood Cells using a Snapshot Hyper-Spectral Imaging System" (2016). Graduate Theses, Dissertations, and Problem Reports. 6519. https://researchrepository.wvu.edu/etd/6519 This Thesis is protected by copyright and/or related rights. It has been brought to you by the The Research Repository @ WVU with permission from the rights-holder(s). You are free to use this Thesis in any way that is permitted by the copyright and related rights legislation that applies to your use. For other uses you must obtain permission from the rights-holder(s) directly, unless additional rights are indicated by a Creative Commons license in the record and/ or on the work itself. This Thesis has been accepted for inclusion in WVU Graduate Theses, Dissertations, and Problem Reports collection by an authorized administrator of The Research Repository @ WVU. For more information, please contact [email protected]. Imaging White Blood Cells using a Snapshot Hyper-Spectral Imaging System Christopher John Robison Thesis submitted to the Benjamin M. Statler College of Engineering and Mineral Resources at West Virginia University In partial fulfillment of the requirements for the degree of Master of Science in Electrical Engineering Jeremy M. Dawson, Ph.D., Chair Thirimachos Bourlai, Ph.D. Christopher J. Kolanko, Ph.D. Lane Department of Computer Science and Electrical Engineering Morgantown, West Virginia 2016 Keywords: Hyper-Spectral Imaging, Medical Imaging, Copyright 2016 Christopher John Robison Abstract Imaging White Blood Cells using a Snapshot Hyper-Spectral Imaging System by Christopher Robison Automated white blood cell (WBC) counting systems process an extracted whole blood sample and provide a cell count. -

Enterprise Applications: 8 Business Communications CHAPTER
Confirming Pages Enterprise Applications: 8 Business Communications CHAPTER SECTION 8.1 SECTION 8.2 Enterprise Systems and Customer Relationship Supply Chain Management Management and Enterprise Resource Planning ■ Building a Connected ■ Customer Relationship Corporation through Management Integrations ■ The Benefits of CRM ■ Supply Chain Management ■ The Challenges of CRM ■ The Benefits of SCM ■ The Future of CRM ■ The Challenges of SCM ■ Enterprise Resource Planning ■ The Future of SCM ■ The Benefits of ERP ■ The Challenges of ERP ■ The Future of Enterprise CHAPTER OUTLINE CHAPTER OUTLINE Systems: Integrating SCM, CRM, and ERP What’s in IT for me? This chapter introduces high-profile strategic initiatives an organization can undertake to help it gain competi- tive advantages and business efficiencies—supply chain management, customer relationship management, and enterprise resource planning. At the simplest level, organizations implement enterprise systems to gain efficiency in business processes, effectiveness in supply chains, and an overall understanding of customer needs and behav- iors. Successful organizations recognize the competitive advantage of maintaining healthy relationships with employees, customers, suppliers, and partners. Doing so has a direct and positive effect on revenue and greatly adds to a company’s profitability. You, as a business student, must understand the critical relationship your business will have with its employees, customers, suppliers, and partners. You must also understand how to analyze your organizational data to ensure you are not just meeting but exceeding expectations. Enterprises are technologically empowered as never before to reach their goals of integrating, analyzing, and making intelligent business decisions. bbal76825_ch08_285-330.inddal76825_ch08_285-330.indd 228686 111/11/101/11/10 110:530:53 PPMM Confirming Pages opening case study Zappos Is Passionate for Customers Tony Hsieh’s first entrepreneurial effort began at the age of 12 when he started his own custom button business. -

Microsoft Acquires Massive, Inc
S T A N F O R D U N I V E R S I T Y! 2 0 0 7 - 3 5 3 - 1! W W W . C A S E W I K I . O R G! R e v . M a y 2 9 , 2 0 0 7 MICROSOFT ACQUIRES MASSIVE, INC. May 4th, 2006 T A B L E O F C O N T E N T S 1. Introduction 2. Industry Overview 2.1. The Advertising Opportunity Within Video Games 2.2. Market Size and Demographics 2.3. Video Games and Advertising 2.4. Market Dynamics 3. Massive, Inc. ! Company Background 3.1. Founding of Massive 3.2. The Financing of Massive 3.3. Product Launch / Technology 3.4. The Massive / Microsoft Deal 4. Microsoft, Inc. within the Video Game Industry 4.1. Role as a Game Publisher / Developer 4.2. Acquisitions 4.3. Role as an Electronic Advertising Network 4.4. Statements Regarding the Acquisition of Massive, Inc. 5. Exhibits 5.1. Table of Exhibits 6. References ! 2 0 0 7 - 3 5 3 - 1! M i c r o s o f t A c q u i s i t i o n o f M a s s i v e , I n c .! I N T R O D U C T I O N In May 2007, Microsoft Corporation was a company in transition. Despite decades of dominance in its core markets of operating systems and desktop productivity software, Mi! crosoft was under tremendous pressure to create strongholds in new market spaces. -

Redalyc.Software Defined Radio: Basic Principles and Applications
Facultad de Ingeniería ISSN: 0121-1129 [email protected] Universidad Pedagógica y Tecnológica de Colombia Colombia Machado-Fernández, José Raúl Software Defined Radio: Basic Principles and Applications Facultad de Ingeniería, vol. 24, núm. 38, enero-junio, 2015, pp. 79-96 Universidad Pedagógica y Tecnológica de Colombia Tunja, Colombia Available in: http://www.redalyc.org/articulo.oa?id=413940775007 How to cite Complete issue Scientific Information System More information about this article Network of Scientific Journals from Latin America, the Caribbean, Spain and Portugal Journal's homepage in redalyc.org Non-profit academic project, developed under the open access initiative José Raúl Machado-Fernández ISSN 0121-1129 eISSN 2357-5328 Software Defined Radio: Basic Principles and Applications Software Defined Radio: Principios y aplicaciones básicas Software Defined Radio: Princípios e Aplicações básicas Fecha de Recepción: 29 de Septiembre de 2014 José Raúl Machado-Fernández* Fecha de Aceptación: 15 de Noviembre de 2014 Abstract The author makes a review of the SDR (Software Defined Radio) technology, including hardware schemes and application fields. A low performance device is presented and several tests are executed with it using free software. With the acquired experience, SDR employment opportunities are identified for low-cost solutions that can solve significant problems. In addition, a list of the most important frameworks related to the technology developed in the last years is offered, recommending the use of three of them. Keywords: Software Defined Radio (SDR), radiofrequencies receiver, radiofrequencies transmitter, radio development frameworks, superheterodyne receiver, SDR hardware devices, SDR-Sharp, RTLSDR-Scanner. Resumen El autor realiza una revisión de la tecnología Radio Definido por Software (SDR, Software Defined Radio) incluyendo esquemas de hardware y campos de aplicación. -
Microsoft from Wikipedia, the Free Encyclopedia Jump To: Navigation, Search
Microsoft From Wikipedia, the free encyclopedia Jump to: navigation, search Coordinates: 47°38′22.55″N 122°7′42.42″W / 47.6395972°N 122.12845°W / 47.6395972; -122.12845 Microsoft Corporation Public (NASDAQ: MSFT) Dow Jones Industrial Average Type Component S&P 500 Component Computer software Consumer electronics Digital distribution Computer hardware Industry Video games IT consulting Online advertising Retail stores Automotive software Albuquerque, New Mexico Founded April 4, 1975 Bill Gates Founder(s) Paul Allen One Microsoft Way Headquarters Redmond, Washington, United States Area served Worldwide Key people Steve Ballmer (CEO) Brian Kevin Turner (COO) Bill Gates (Chairman) Ray Ozzie (CSA) Craig Mundie (CRSO) Products See products listing Services See services listing Revenue $62.484 billion (2010) Operating income $24.098 billion (2010) Profit $18.760 billion (2010) Total assets $86.113 billion (2010) Total equity $46.175 billion (2010) Employees 89,000 (2010) Subsidiaries List of acquisitions Website microsoft.com Microsoft Corporation is an American public multinational corporation headquartered in Redmond, Washington, USA that develops, manufactures, licenses, and supports a wide range of products and services predominantly related to computing through its various product divisions. Established on April 4, 1975 to develop and sell BASIC interpreters for the Altair 8800, Microsoft rose to dominate the home computer operating system (OS) market with MS-DOS in the mid-1980s, followed by the Microsoft Windows line of OSes. Microsoft would also come to dominate the office suite market with Microsoft Office. The company has diversified in recent years into the video game industry with the Xbox and its successor, the Xbox 360 as well as into the consumer electronics market with Zune and the Windows Phone OS. -

Planning and Engineering Guide
Nortel CallPilot Planning and Engineering Guide NN44200-200 . Document status: Standard Document version: 01.13 Document date: 22 July 2009 Copyright © 2007-2009, Nortel Networks All Rights Reserved. Sourced in Canada The information in this document is subject to change without notice. The statements, configurations, technical data, and recommendations in this document are believed to be accurate and reliable, but are presented without express or implied warranty. Users must take full responsibility for their applications of any products specified in this document. The information in this document is proprietary to Nortel Networks. The process of transmitting data and call messaging between the CallPilot server and the switch or the system is proprietary to Nortel Networks. Any other use of the data and the transmission process is a violation of the user license unless specifically authorized in writing by Nortel Networks prior to such use. Violations of the license by alternative usage of any portion of this process or the related hardware constitutes grounds for an immediate termination of the license and Nortel Networks reserves the right to seek all allowable remedies for such breach. Trademarks Nortel Networks, the Nortel Networks logo, the Globemark, and Unified Networks, BNR, CallPilot, Communication Server, DMS, DMS-100, DMS-250, DMS-MTX, DMS-SCP, DPN, Dualmode, Helmsman, IVR, MAP, Meridian, Meridian 1, Meridian Link, Meridian Mail, Norstar, SL-1, SL-100, Succession, Supernode, Symposium, Telesis, and Unity are trademarks of Nortel Networks. 3COM is a trademark of 3Com Corporation. ADOBE is a trademark of Adobe Systems Incorporated. ATLAS is a trademark of Quantum Corporation. BLACKBERRY is a trademark of Research in Motion Limited. -

Microsoft Corporation
Microsoft Corporation General Company Information Address One Microsoft Way Redmond, WA 98052-6399 United States Phone: 425 882-8080 Fax: 425 936-7329 Country United States Ticker MSFT Date of Incorporation June 1981 , WA, United States Number of Employees 89,000 (Approximate Full-Time as of 06/30/2010) Number of Shareholders 138,568 (record) (as of 07/20/2010) Company Website www.microsoft.com Annual Meeting Date In November Mergent Dividend Achiever No Closing Price As of 02/18/2011 : 27.06 02/20/2011 1 Mergent, Inc. Microsoft Corporation Business Description Industry Internet & Software NAICS Primary NAICS: 511210 - Software Publishers Secondary NAICS: 334119 - Other Computer Peripheral Equipment Manufacturing 423430 - Computer and Computer Peripheral Equipment and Software Merchant Wholesalers 541519 - Other Computer Related Services SIC Primary SIC: 7372 - Prepackaged software Secondary SIC: 3577 - Computer peripheral equipment, nec 7379 - Computer related services, nec Business Description Microsoft is engaged in developing, manufacturing, licensing, and supporting a range of software products and services for several computing devices. Co.'s software products and services include operating systems for personal computers, servers, and intelligent devices; server applications for distributed computing environments; information worker productivity applications; business and computing applications; software development tools; and video games. Co. also provides consulting and product and application support services, as well as trains and certifies computer system integrators and developers. In addition, Co. designs and sells hardware including the Xbox 360 gaming and entertainment console and accessories, the Zune digital music and entertainment device and accessories, and Microsoft personal computer (PC) hardware products. Co. operates through five segments. -

United States Patent (10) Patent N0.: US 7,266,767 B2 Parker (45) Date of Patent: Sep
US007266767B2 (12) United States Patent (10) Patent N0.: US 7,266,767 B2 Parker (45) Date of Patent: Sep. 4, 2007 (54) METHOD AND APPARATUS FOR 5,966,386 A 10/1999 MaegaWa AUTOMATED AUTHORING AND 6,012,098 A * 1/2000 Bayeh et al. ............. .. 709/246 MARKETING 6,026,417 A * 2/2000 Ross et al. ................ .. 715/517 (76) Inventor: Philip M. Parker, 12874 HarWick La., 6’026’809 A 2/2000 Abrams et al' San Diego’ A Nehab et al. 6,029,195 A 2/2000 HerZ ( * ) Notice: Subject to any disclaimer, the term of this 6,052,717 A 4/2000 Reynolds et a1. patent is extended or adjusted under 35 6,154,213 A 11/2000 Rennison et a1, U50 1540’) by 0 days- 6,374,271 B1 4/2002 Shimizu et al. (21) APPI' NO‘: 11l261’631 6,393,196 B1 5/2002 Yamane et a1. 6,393,388 Bl* 5/2002 FranZ et al. ................. .. 704/4 (22) Filed: Oct. 31, 2005 (65) Prior Publication Data C t' d Us 2006/0064631 A1 Mar. 23, 2006 ( on “me ) OTHER PUBLICATIONS Related US. Application Data _ _ _ _ “eTranslate Joins Forces With MSN LinkEXchange to Help Small (63) Commuanon of appl1cat1on NO~ 09/723,522: ?led on Businesses Reach International Audience on the Web” Aug. 30, NOV- 27, 2000, now abandoned 1999 http://WWW.microsoft.com/presspass/press/1999/aug99/ etranslatepr.mspx.* (51) Int. Cl. G06F 17/00 (2006.01) (Continued) (52) US. Cl. ....... ...... .., ................... .. 715/517; 715/523 Primary Examineristephen Hong (58) Field of Classi?cation Search ............... -

Razvoj Programske Opreme
Pod lupo: Google AdWords • IT oddelek za nove čase? • Pametna telefonija • Upravljanje s kakovostjo podatkov • Predstavljamo: Amazon AWS • Intervju: Boštjan Bregar, direktor podjetja Marg NOVE TEHNOLOGIJE ZA POSLOVNI SVET Pomlad 2013 / 5,90 € www.monitorpro.si Razvoj programske opreme Vsi, ki se že dolgo ukvarjamo s programsko opremo, vemo iz izkušenj vemo, da ogromno projektov nikoli ne zaključi faze integracije, saj je bolečina povezana z integracijo nove programske opreme v obstoječo okolje velikokrat preprosto prevelika. Kaj je narobe? 01/13 BESEDA UREDNIKA Samo naprej! Včasih se zdi, kot da Slovenci nimamo mere. Ni dovolj, da smo se znašli plačevali drage ure programerjev. O njih v intervju- v skupini držav, ki jih je ekonomska kriza najbolj prizadela. Ne, da je vse ju med drugim spregovori Boštjan Bregar, prav tako skupaj težje rešljivo, smo si omislili krizo na političnem in še na kakšnem eden tistih, ki so se s poslom pogumno napotili prek področju. meja domovine. Tudi on ugotavlja, da odličen izdelek ako stanje traja že malone pet let, gospodar- še ne pomeni denarja v žepu. Treba je namreč navdu- stvo pa se medtem opoteka in čaka, da bodo šiti uporabnike in ga znati prodati. tisti, ki so za to izvoljeni in plačani, končno že Zato smo pod drobnogled vzeli najhitreje rasto- ustvarili razmere, da izvlečemo voz iz blata. či trg oglaševanja, Googlov AdWords. Kaj se izplača TPa ga ne. Kot kaže, še vedno nismo dosegli tistega dna, in kako se pri tem čim bolj izogniti brcam v meglo? kjer bi končno spregledali, da bo treba začeti znova. Ker vemo, da so naša podjetja majhna, da si večina Na novih temeljih, tako ekonomskih kot tistih člo- ne more privoščiti pomoči plačanih strokovnjakov in veških. -

Microsoft 1999 Annual Report FINANCIAL HIGHLIGHTS Msft in Millions, Except Earnings Per Share
Microsoft_1999_Annual Report FINANCIAL HIGHLIGHTS msft In millions, except earnings per share Year Ended June 30 1995 1996 1997 1998 1999 Revenue $6,075 $9,050 $11,936 $15,262 $19,747 Net income 1,453 2,195 3,454 4,490 7,785 Diluted earnings per share1 0.29 0.43 0.66 0.84 1.42 Cash and short-term investments 4,750 6,940 8,966 13,927 17,236 Total assets 7,210 10,093 14,387 22,357 37,156 Stockholders’ equity 5,333 6,908 10,777 16,627 28,438 1 Diluted earnings per share have been restated to reflect a two-for-one stock split in March 1999. 2 FELLOW SHAREHOLDERS > Microsoft continued to perform strongly in 1999. Our customers count on us to provide great software that helps them communicate more effectively, work more productively, learn more creatively, and make the most of their leisure time. We worked hard to meet those needs and to set the standard for features, functionality, simplicity, and seamless integration with the Internet in all of our products. The result was remarkable growth and record revenue. In the years ahead, we will see accelerating change in the software industry, as the computing needs of our customers start to move beyond the PC into a “PC-Plus” world. The PC will undoubtedly remain at the heart of computing at home, work, and school, but it will be joined by numerous new intelligent devices and appliances, from handheld computers and auto PCs to Internet-enabled cellular phones. More software will be delivered over the Internet, and the boundary between online services and software products will blur. -
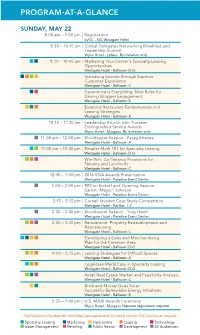
Program-At-A-Glance
PROGRAM-AT-A-GLANCE SUNDAY, MAY 22 8:00 am – 5:00 pm I Registration LVCC - N3, Westgate Hotel 8:30 – 10:15 am I Global Delegates Networking Breakfast and Leadership Summit Wynn Hotel - Lafleur By invitation only 9:30 – 10:45 am I Marketing Your Center’s Specialty Leasing Opportunities Westgate Hotel - Ballroom D-G Increasing Income through Superior Customer Experience Westgate Hotel - Ballroom C Experience is Everything: New Rules for Driving Shopper Engagement Westgate Hotel - Ballroom B Essential Restaurant Fundamentals and Leasing Strategies Westgate Hotel - Ballroom A 10:15 – 11:30 am I Leadership Brunch with Trustees Distinguished Service Awards Wynn Hotel - Margaux By invitation only 11:00 am – 12:00 pm I Blockbuster Session - Parag Khanna Westgate Hotel - Ballroom A 11:00 am – 12:30 pm I Retailer Math 101 for Specialty Leasing Westgate Hotel - Ballroom D-G Win-Win: Co-Tenancy Provisions for Tenants and Landlords Westgate Hotel - Ballroom C 12:45 – 1:00 pm I 2016 VIVA Awards Presentation Westgate Hotel - Paradise Event Center 1:00 – 2:00 pm I RECon Kickoff and Opening Session - Earvin “Magic” Johnson Westgate Hotel - Paradise Event Center 2:15 – 5:15 pm I Cornell Student Case Study Competition Westgate Hotel - Pavilion 1-2 2:30 – 3:30 pm I Blockbuster Session - Tony Hsieh Westgate Hotel - Paradise Event Center 2:30 – 3:45 pm I Reinvention: Property Redevelopment and Repositioning Westgate Hotel - Ballroom C Developing a Sales and Merchandising Plan for the Common Area Westgate Hotel - Ballroom D-G 4:00 – 5:15 pm I Leasing Strategies for Difficult Spaces Westgate Hotel - Ballroom A Legalease Made Easy in Specialty Leasing Westgate Hotel - Ballroom D-G Retail Real Estate Market and Feasibility Analysis Westgate Hotel - Ballroom C Brick and Mortar Goes Solar: Successful Renewable Energy Initiatives Westgate Hotel - Ballroom B 5:30 – 7:00 pm I U.S. -
Serial Portals
Serial portals http://www.redherring.com/Home/7404 Sign Up | Login NEWS BLOG EVENTS RESEARCH VIDEO AWARDS TOP STORIES FINANCE INTERNET CLEANTECH COMMUNICATIONS MEDIA COMPUTING BIOSCIENCES SECURITY MAGAZINE ARCHIVES ADVERTISEMENT FEEDS rpc opml RSS for this group All Articles Comments News Events WIKI Custom RSS feeds ADVERTISEMENT 1 of 4 10/26/09 4:31 PM Serial portals http://www.redherring.com/Home/7404 Serial portals on 29 February 2000, 22:00 by Niall McKay One way of attacking the wickedly fragmented small-business market is to offer a product that every company needs, like accounting software, office supplies, or, these days, Web-site creation. Another approach -- unimaginable before the Internet -- is to be all things to all businesses. In the past six months, venture capitalists and established technology companies have pumped hundreds of millions of dollars into companies doing just that. Unlike sites that focus on large corporate markets (which tend to address narrow vertical segments), the Internet portals focusing on small businesses intend to help users streamline everything from office-supply ordering and payroll administration to bad-debt collection and Web advertising. The market for such services is certainly untapped: although more than half of all small businesses now have access to the Internet, less than 10 percent have electronic-commerce Web sites, according to most studies, and even fewer integrate the Internet into their day-to-day business beyond email and research. But now dozens of sites are vying to help them do so, with AllBusiness.com, GoTo.com,DigitalWork.com , Winstar'sOffice.com, and Microsoft'sbCentral among the most prominent.