DOCSLIB.ORG

Manifolds and the Shape of the Universe

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Manifolds and the Shape of the Universe Manifolds and the Shape of the Universe Stacy Hoehn Vanderbilt University [email protected] July 13, 2010 Stacy Hoehn Manifolds and the Shape of the Universe Stretching, shrinking, bending, and twisting are allowed. Examples of Homeomorphic Objects: What Does \Shape" Mean to a Topologist? In topology, two objects have the same shape if one can be deformed into the other without cutting or gluing. Objects with the same shape are called homeomorphic. Stacy Hoehn Manifolds and the Shape of the Universe Examples of Homeomorphic Objects: What Does \Shape" Mean to a Topologist? In topology, two objects have the same shape if one can be deformed into the other without cutting or gluing. Objects with the same shape are called homeomorphic. Stretching, shrinking, bending, and twisting are allowed. Stacy Hoehn Manifolds and the Shape of the Universe What Does \Shape" Mean to a Topologist? In topology, two objects have the same shape if one can be deformed into the other without cutting or gluing. Objects with the same shape are called homeomorphic. Stretching, shrinking, bending, and twisting are allowed. Examples of Homeomorphic Objects: Stacy Hoehn Manifolds and the Shape of the Universe A torus and a sphere are not homeomorphic. Homeomorphic or Not? A doughnut and a coffee cup are homeomorphic. Stacy Hoehn Manifolds and the Shape of the Universe Homeomorphic or Not? A doughnut and a coffee cup are homeomorphic. A torus and a sphere are not homeomorphic. Stacy Hoehn Manifolds and the Shape of the Universe 2 Locally, they both look two-dimensional Euclidean space R . The torus and the sphere are both called 2-manifolds because they share this property. 2-Manifolds Even though the torus and sphere are not homeomorphic, they do have something in common. Stacy Hoehn Manifolds and the Shape of the Universe The torus and the sphere are both called 2-manifolds because they share this property. 2-Manifolds Even though the torus and sphere are not homeomorphic, they do have something in common. 2 Locally, they both look two-dimensional Euclidean space R . Stacy Hoehn Manifolds and the Shape of the Universe 2-Manifolds Even though the torus and sphere are not homeomorphic, they do have something in common. 2 Locally, they both look two-dimensional Euclidean space R . The torus and the sphere are both called 2-manifolds because they share this property. Stacy Hoehn Manifolds and the Shape of the Universe Examples: 1-manifolds: 2-manifolds: 3 3-manifolds: R and the universe n-Manifolds Definition An n-manifold is a topological space that locally looks like n n-dimensional Euclidean space R . Stacy Hoehn Manifolds and the Shape of the Universe n-Manifolds Definition An n-manifold is a topological space that locally looks like n n-dimensional Euclidean space R . Examples: 1-manifolds: 2-manifolds: 3 3-manifolds: R and the universe Stacy Hoehn Manifolds and the Shape of the Universe The Surface of the Earth Locally, the surface of the Earth looks like a 2-dimensional plane, so it is a 2-manifold. If we only saw this local picture, it would be reasonable to believe that the Earth is an infinite plane, a sphere, a torus, or any other 2-manifold. What other 2-manifold possibilities are there, and how can we eliminate the other possibilities? Stacy Hoehn Manifolds and the Shape of the Universe Yes! There are actually infinitely many compact 2-manifolds. But fortunately they are all made out of simple building blocks. Compact 2-Manifolds We will restrict our attention to 2-manifolds that are finite. These are called compact 2-manifolds. The sphere and torus are both compact 2-manifolds. Are there any others? Stacy Hoehn Manifolds and the Shape of the Universe Compact 2-Manifolds We will restrict our attention to 2-manifolds that are finite. These are called compact 2-manifolds. The sphere and torus are both compact 2-manifolds. Are there any others? Yes! There are actually infinitely many compact 2-manifolds. But fortunately they are all made out of simple building blocks. Stacy Hoehn Manifolds and the Shape of the Universe This square, with its opposite sides identified, helps us depict the torus in the plane. The Torus To help us visualize the other compact 2-manifolds, we will first view the torus a little bit differently. We will construct a torus by gluing together opposite edges of a square. Stacy Hoehn Manifolds and the Shape of the Universe The Torus To help us visualize the other compact 2-manifolds, we will first view the torus a little bit differently. We will construct a torus by gluing together opposite edges of a square. This square, with its opposite sides identified, helps us depict the torus in the plane. Stacy Hoehn Manifolds and the Shape of the Universe You would see infinitely many copies of yourself in every direction! The Torus (continued) What would you see if you were a two-dimensional being living in a torus? Stacy Hoehn Manifolds and the Shape of the Universe The Torus (continued) What would you see if you were a two-dimensional being living in a torus? You would see infinitely many copies of yourself in every direction! Stacy Hoehn Manifolds and the Shape of the Universe The M¨obiusBand A M¨obiusband is constructed from a square by gluing the left side to the right side of the square after performing a half-twist. Stacy Hoehn Manifolds and the Shape of the Universe Note: The M¨obiusband is not a manifold because it has an edge. (It is called a manifold-with-boundary.) The M¨obiusBand (continued) A M¨obiusband contains an orientation-reversing curve. Clockwise becomes counterclockwise along this curve! Stacy Hoehn Manifolds and the Shape of the Universe The M¨obiusBand (continued) A M¨obiusband contains an orientation-reversing curve. Clockwise becomes counterclockwise along this curve! Note: The M¨obiusband is not a manifold because it has an edge. (It is called a manifold-with-boundary.) Stacy Hoehn Manifolds and the Shape of the Universe The Klein bottle is a 2-manifold. The Klein Bottle A Klein bottle is constructed from a square by gluing together the left and right edges the same way as for a torus, but now the top edge is flipped before being glued to the bottom edge. Stacy Hoehn Manifolds and the Shape of the Universe The Klein Bottle A Klein bottle is constructed from a square by gluing together the left and right edges the same way as for a torus, but now the top edge is flipped before being glued to the bottom edge. The Klein bottle is a 2-manifold. Stacy Hoehn Manifolds and the Shape of the Universe You would see infinitely many copies of yourself in every direction, but sometimes you would be flipped! The Klein Bottle (continued) What would you see if you were a two-dimensional being living in a Klein bottle? Stacy Hoehn Manifolds and the Shape of the Universe The Klein Bottle (continued) What would you see if you were a two-dimensional being living in a Klein bottle? You would see infinitely many copies of yourself in every direction, but sometimes you would be flipped! Stacy Hoehn Manifolds and the Shape of the Universe The Klein Bottle (continued) The Klein bottle contains an orientation-reversing curve since it contains a M¨obiusband. Manifolds that contain an orientation-reversing curve are called nonorientable. Manifolds that do not contain an orientation-reversing curve are called orientable. Stacy Hoehn Manifolds and the Shape of the Universe The projective plane is a nonorientable 2-manifold that can be obtained from a disk by making different identifications. The Sphere and Projective Plane The sphere is an orientable 2-manifold that can be obtained from a disk as shown below. Stacy Hoehn Manifolds and the Shape of the Universe The Sphere and Projective Plane The sphere is an orientable 2-manifold that can be obtained from a disk as shown below. The projective plane is a nonorientable 2-manifold that can be obtained from a disk by making different identifications. Stacy Hoehn Manifolds and the Shape of the Universe Amazingly, every compact 2-manifold is homeomorphic to either a sphere (orientable), a connected sum of tori (orientable), or a connected sum of projective planes (nonorientable). Connected Sum Given two 2-manifolds, we can create a new 2-manifold by taking their connected sum. To take the connected sum of two 2-manifolds, remove the inside of a small disk from each of them and then glue the two boundary circles of these disks together. Stacy Hoehn Manifolds and the Shape of the Universe Connected Sum Given two 2-manifolds, we can create a new 2-manifold by taking their connected sum. To take the connected sum of two 2-manifolds, remove the inside of a small disk from each of them and then glue the two boundary circles of these disks together. Amazingly, every compact 2-manifold is homeomorphic to either a sphere (orientable), a connected sum of tori (orientable), or a connected sum of projective planes (nonorientable). Stacy Hoehn Manifolds and the Shape of the Universe There are infinitely many 3-manifolds. A priori, any one of these 3-manifolds could be the shape of the universe. The Shape of the Universe No matter where we have been in the universe so far, if we choose a spot and travel out from it a short distance in all directions, we enclose a space that resembles a ball in 3-dimensional Euclidean space. Thus, the universe appears to be some 3-manifold.
Load more

Recommended publications
  • Note on 6-Regular Graphs on the Klein Bottle Michiko Kasai [email protected]
    Theory and Applications of Graphs Volume 4 | Issue 1 Article 5 2017 Note On 6-regular Graphs On The Klein Bottle Michiko Kasai [email protected] Naoki Matsumoto Seikei University, [email protected] Atsuhiro Nakamoto Yokohama National University, [email protected] Takayuki Nozawa [email protected] Hiroki Seno [email protected] See next page for additional authors Follow this and additional works at: https://digitalcommons.georgiasouthern.edu/tag Part of the Discrete Mathematics and Combinatorics Commons Recommended Citation Kasai, Michiko; Matsumoto, Naoki; Nakamoto, Atsuhiro; Nozawa, Takayuki; Seno, Hiroki; and Takiguchi, Yosuke (2017) "Note On 6-regular Graphs On The Klein Bottle," Theory and Applications of Graphs: Vol. 4 : Iss. 1 , Article 5. DOI: 10.20429/tag.2017.040105 Available at: https://digitalcommons.georgiasouthern.edu/tag/vol4/iss1/5 This article is brought to you for free and open access by the Journals at Digital Commons@Georgia Southern. It has been accepted for inclusion in Theory and Applications of Graphs by an authorized administrator of Digital Commons@Georgia Southern. For more information, please contact [email protected]. Note On 6-regular Graphs On The Klein Bottle Authors Michiko Kasai, Naoki Matsumoto, Atsuhiro Nakamoto, Takayuki Nozawa, Hiroki Seno, and Yosuke Takiguchi This article is available in Theory and Applications of Graphs: https://digitalcommons.georgiasouthern.edu/tag/vol4/iss1/5 Kasai et al.: 6-regular graphs on the Klein bottle Abstract Altshuler [1] classified 6-regular graphs on the torus, but Thomassen [11] and Negami [7] gave different classifications for 6-regular graphs on the Klein bottle. In this note, we unify those two classifications, pointing out their difference and similarity.
    [Show full text]
  • Examples of Manifolds
    Examples of Manifolds Example 1 (Open Subset of IRn) Any open subset, O, of IRn is a manifold of dimension n. One possible atlas is A = (O, ϕid) , where ϕid is the identity map. That is, ϕid(x) = x. n Of course one possible choice of O is IR itself. Example 2 (The Circle) The circle S1 = (x,y) ∈ IR2 x2 + y2 = 1 is a manifold of dimension one. One possible atlas is A = {(U , ϕ ), (U , ϕ )} where 1 1 1 2 1 y U1 = S \{(−1, 0)} ϕ1(x,y) = arctan x with − π < ϕ1(x,y) <π ϕ1 1 y U2 = S \{(1, 0)} ϕ2(x,y) = arctan x with 0 < ϕ2(x,y) < 2π U1 n n n+1 2 2 Example 3 (S ) The n–sphere S = x =(x1, ··· ,xn+1) ∈ IR x1 +···+xn+1 =1 n A U , ϕ , V ,ψ i n is a manifold of dimension . One possible atlas is 1 = ( i i) ( i i) 1 ≤ ≤ +1 where, for each 1 ≤ i ≤ n + 1, n Ui = (x1, ··· ,xn+1) ∈ S xi > 0 ϕi(x1, ··· ,xn+1)=(x1, ··· ,xi−1,xi+1, ··· ,xn+1) n Vi = (x1, ··· ,xn+1) ∈ S xi < 0 ψi(x1, ··· ,xn+1)=(x1, ··· ,xi−1,xi+1, ··· ,xn+1) n So both ϕi and ψi project onto IR , viewed as the hyperplane xi = 0. Another possible atlas is n n A2 = S \{(0, ··· , 0, 1)}, ϕ , S \{(0, ··· , 0, −1)},ψ where 2x1 2xn ϕ(x , ··· ,xn ) = , ··· , 1 +1 1−xn+1 1−xn+1 2x1 2xn ψ(x , ··· ,xn ) = , ··· , 1 +1 1+xn+1 1+xn+1 are the stereographic projections from the north and south poles, respectively.
    [Show full text]
  • An Introduction to Topology the Classification Theorem for Surfaces by E
    An Introduction to Topology An Introduction to Topology The Classification theorem for Surfaces By E. C. Zeeman Introduction. The classification theorem is a beautiful example of geometric topology. Although it was discovered in the last century*, yet it manages to convey the spirit of present day research. The proof that we give here is elementary, and its is hoped more intuitive than that found in most textbooks, but in none the less rigorous. It is designed for readers who have never done any topology before. It is the sort of mathematics that could be taught in schools both to foster geometric intuition, and to counteract the present day alarming tendency to drop geometry. It is profound, and yet preserves a sense of fun. In Appendix 1 we explain how a deeper result can be proved if one has available the more sophisticated tools of analytic topology and algebraic topology. Examples. Before starting the theorem let us look at a few examples of surfaces. In any branch of mathematics it is always a good thing to start with examples, because they are the source of our intuition. All the following pictures are of surfaces in 3-dimensions. In example 1 by the word “sphere” we mean just the surface of the sphere, and not the inside. In fact in all the examples we mean just the surface and not the solid inside. 1. Sphere. 2. Torus (or inner tube). 3. Knotted torus. 4. Sphere with knotted torus bored through it. * Zeeman wrote this article in the mid-twentieth century. 1 An Introduction to Topology 5.
    [Show full text]
  • The Sphere Project
    ;OL :WOLYL 7YVQLJ[ +XPDQLWDULDQ&KDUWHUDQG0LQLPXP 6WDQGDUGVLQ+XPDQLWDULDQ5HVSRQVH ;OL:WOLYL7YVQLJ[ 7KHULJKWWROLIHZLWKGLJQLW\ ;OL:WOLYL7YVQLJ[PZHUPUP[PH[P]L[VKL[LYTPULHUK WYVTV[LZ[HUKHYKZI`^OPJO[OLNSVIHSJVTT\UP[` /\THUP[HYPHU*OHY[LY YLZWVUKZ[V[OLWSPNO[VMWLVWSLHMMLJ[LKI`KPZHZ[LYZ /\THUP[HYPHU >P[O[OPZ/HUKIVVR:WOLYLPZ^VYRPUNMVYH^VYSKPU^OPJO [OLYPNO[VMHSSWLVWSLHMMLJ[LKI`KPZHZ[LYZ[VYLLZ[HISPZO[OLPY *OHY[LYHUK SP]LZHUKSP]LSPOVVKZPZYLJVNUPZLKHUKHJ[LK\WVUPU^H`Z[OH[ YLZWLJ[[OLPY]VPJLHUKWYVTV[L[OLPYKPNUP[`HUKZLJ\YP[` 4PUPT\T:[HUKHYKZ This Handbook contains: PU/\THUP[HYPHU (/\THUP[HYPHU*OHY[LY!SLNHSHUKTVYHSWYPUJPWSLZ^OPJO HUK YLÅLJ[[OLYPNO[ZVMKPZHZ[LYHMMLJ[LKWVW\SH[PVUZ 4PUPT\T:[HUKHYKZPU/\THUP[HYPHU9LZWVUZL 9LZWVUZL 7YV[LJ[PVU7YPUJPWSLZ *VYL:[HUKHYKZHUKTPUPT\TZ[HUKHYKZPUMV\YRL`SPMLZH]PUN O\THUP[HYPHUZLJ[VYZ!>H[LYZ\WWS`ZHUP[H[PVUHUKO`NPLUL WYVTV[PVU"-VVKZLJ\YP[`HUKU\[YP[PVU":OLS[LYZL[[SLTLU[HUK UVUMVVKP[LTZ"/LHS[OHJ[PVU;OL`KLZJYPILwhat needs to be achieved in a humanitarian response in order for disaster- affected populations to survive and recover in stable conditions and with dignity. ;OL:WOLYL/HUKIVVRLUQV`ZIYVHKV^ULYZOPWI`HNLUJPLZHUK PUKP]PK\HSZVMMLYPUN[OLO\THUP[HYPHUZLJ[VYH common language for working together towards quality and accountability in disaster and conflict situations ;OL:WOLYL/HUKIVVROHZHU\TILYVMºJVTWHUPVU Z[HUKHYKZ»L_[LUKPUNP[ZZJVWLPUYLZWVUZL[VULLKZ[OH[ OH]LLTLYNLK^P[OPU[OLO\THUP[HYPHUZLJ[VY ;OL:WOLYL7YVQLJ[^HZPUP[PH[LKPU I`HU\TILY VMO\THUP[HYPHU5.6ZHUK[OL9LK*YVZZHUK 9LK*YLZJLU[4V]LTLU[ ,+0;065 7KHB6SKHUHB3URMHFWBFRYHUBHQBLQGG The Sphere Project Humanitarian Charter and Minimum Standards in Humanitarian Response Published by: The Sphere Project Copyright@The Sphere Project 2011 Email: [email protected] Website : www.sphereproject.org The Sphere Project was initiated in 1997 by a group of NGOs and the Red Cross and Red Crescent Movement to develop a set of universal minimum standards in core areas of humanitarian response: the Sphere Handbook.
    [Show full text]
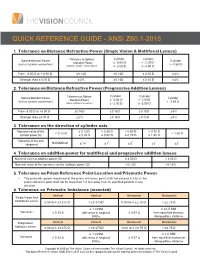
  • Quick Reference Guide - Ansi Z80.1-2015
    QUICK REFERENCE GUIDE - ANSI Z80.1-2015 1. Tolerance on Distance Refractive Power (Single Vision & Multifocal Lenses) Cylinder Cylinder Sphere Meridian Power Tolerance on Sphere Cylinder Meridian Power ≥ 0.00 D > - 2.00 D (minus cylinder convention) > -4.50 D (minus cylinder convention) ≤ -2.00 D ≤ -4.50 D From - 6.50 D to + 6.50 D ± 0.13 D ± 0.13 D ± 0.15 D ± 4% Stronger than ± 6.50 D ± 2% ± 0.13 D ± 0.15 D ± 4% 2. Tolerance on Distance Refractive Power (Progressive Addition Lenses) Cylinder Cylinder Sphere Meridian Power Tolerance on Sphere Cylinder Meridian Power ≥ 0.00 D > - 2.00 D (minus cylinder convention) > -3.50 D (minus cylinder convention) ≤ -2.00 D ≤ -3.50 D From -8.00 D to +8.00 D ± 0.16 D ± 0.16 D ± 0.18 D ± 5% Stronger than ±8.00 D ± 2% ± 0.16 D ± 0.18 D ± 5% 3. Tolerance on the direction of cylinder axis Nominal value of the ≥ 0.12 D > 0.25 D > 0.50 D > 0.75 D < 0.12 D > 1.50 D cylinder power (D) ≤ 0.25 D ≤ 0.50 D ≤ 0.75 D ≤ 1.50 D Tolerance of the axis Not Defined ° ° ° ° ° (degrees) ± 14 ± 7 ± 5 ± 3 ± 2 4. Tolerance on addition power for multifocal and progressive addition lenses Nominal value of addition power (D) ≤ 4.00 D > 4.00 D Nominal value of the tolerance on the addition power (D) ± 0.12 D ± 0.18 D 5. Tolerance on Prism Reference Point Location and Prismatic Power • The prismatic power measured at the prism reference point shall not exceed 0.33Δ or the prism reference point shall not be more than 1.0 mm away from its specified position in any direction.
    [Show full text]
  • THE DIMENSION of a VECTOR SPACE 1. Introduction This Handout
    THE DIMENSION OF A VECTOR SPACE KEITH CONRAD 1. Introduction This handout is a supplementary discussion leading up to the definition of dimension of a vector space and some of its properties. We start by defining the span of a finite set of vectors and linear independence of a finite set of vectors, which are combined to define the all-important concept of a basis. Definition 1.1. Let V be a vector space over a field F . For any finite subset fv1; : : : ; vng of V , its span is the set of all of its linear combinations: Span(v1; : : : ; vn) = fc1v1 + ··· + cnvn : ci 2 F g: Example 1.2. In F 3, Span((1; 0; 0); (0; 1; 0)) is the xy-plane in F 3. Example 1.3. If v is a single vector in V then Span(v) = fcv : c 2 F g = F v is the set of scalar multiples of v, which for nonzero v should be thought of geometrically as a line (through the origin, since it includes 0 · v = 0). Since sums of linear combinations are linear combinations and the scalar multiple of a linear combination is a linear combination, Span(v1; : : : ; vn) is a subspace of V . It may not be all of V , of course. Definition 1.4. If fv1; : : : ; vng satisfies Span(fv1; : : : ; vng) = V , that is, if every vector in V is a linear combination from fv1; : : : ; vng, then we say this set spans V or it is a spanning set for V . Example 1.5. In F 2, the set f(1; 0); (0; 1); (1; 1)g is a spanning set of F 2.
    [Show full text]
  • Higher Dimensional Conundra
    Higher Dimensional Conundra Steven G. Krantz1 Abstract: In recent years, especially in the subject of harmonic analysis, there has been interest in geometric phenomena of RN as N → +∞. In the present paper we examine several spe- cific geometric phenomena in Euclidean space and calculate the asymptotics as the dimension gets large. 0 Introduction Typically when we do geometry we concentrate on a specific venue in a particular space. Often the context is Euclidean space, and often the work is done in R2 or R3. But in modern work there are many aspects of analysis that are linked to concrete aspects of geometry. And there is often interest in rendering the ideas in Hilbert space or some other infinite dimensional setting. Thus we want to see how the finite-dimensional result in RN changes as N → +∞. In the present paper we study some particular aspects of the geometry of RN and their asymptotic behavior as N →∞. We choose these particular examples because the results are surprising or especially interesting. We may hope that they will lead to further studies. It is a pleasure to thank Richard W. Cottle for a careful reading of an early draft of this paper and for useful comments. 1 Volume in RN Let us begin by calculating the volume of the unit ball in RN and the surface area of its bounding unit sphere. We let ΩN denote the former and ωN−1 denote the latter. In addition, we let Γ(x) be the celebrated Gamma function of L. Euler. It is a helpful intuition (which is literally true when x is an 1We are happy to thank the American Institute of Mathematics for its hospitality and support during this work.
    [Show full text]
  • Graphs on Surfaces, the Generalized Euler's Formula and The
    Graphs on surfaces, the generalized Euler's formula and the classification theorem ZdenˇekDvoˇr´ak October 28, 2020 In this lecture, we allow the graphs to have loops and parallel edges. In addition to the plane (or the sphere), we can draw the graphs on the surface of the torus or on more complicated surfaces. Definition 1. A surface is a compact connected 2-dimensional manifold with- out boundary. Intuitive explanation: • 2-dimensional manifold without boundary: Each point has a neighbor- hood homeomorphic to an open disk, i.e., \locally, the surface looks at every point the same as the plane." • compact: \The surface can be covered by a finite number of such neigh- borhoods." • connected: \The surface has just one piece." Examples: • The sphere and the torus are surfaces. • The plane is not a surface, since it is not compact. • The closed disk is not a surface, since it has a boundary. From the combinatorial perspective, it does not make sense to distinguish between some of the surfaces; the same graphs can be drawn on the torus and on a deformed torus (e.g., a coffee mug with a handle). For us, two surfaces will be equivalent if they only differ by a homeomorphism; a function f :Σ1 ! Σ2 between two surfaces is a homeomorphism if f is a bijection, continuous, and the inverse f −1 is continuous as well. In particular, this 1 implies that f maps simple continuous curves to simple continuous curves, and thus it maps a drawing of a graph in Σ1 to a drawing of the same graph in Σ2.
    [Show full text]
  • MTH 304: General Topology Semester 2, 2017-2018
    MTH 304: General Topology Semester 2, 2017-2018 Dr. Prahlad Vaidyanathan Contents I. Continuous Functions3 1. First Definitions................................3 2. Open Sets...................................4 3. Continuity by Open Sets...........................6 II. Topological Spaces8 1. Definition and Examples...........................8 2. Metric Spaces................................. 11 3. Basis for a topology.............................. 16 4. The Product Topology on X × Y ...................... 18 Q 5. The Product Topology on Xα ....................... 20 6. Closed Sets.................................. 22 7. Continuous Functions............................. 27 8. The Quotient Topology............................ 30 III.Properties of Topological Spaces 36 1. The Hausdorff property............................ 36 2. Connectedness................................. 37 3. Path Connectedness............................. 41 4. Local Connectedness............................. 44 5. Compactness................................. 46 6. Compact Subsets of Rn ............................ 50 7. Continuous Functions on Compact Sets................... 52 8. Compactness in Metric Spaces........................ 56 9. Local Compactness.............................. 59 IV.Separation Axioms 62 1. Regular Spaces................................ 62 2. Normal Spaces................................ 64 3. Tietze's extension Theorem......................... 67 4. Urysohn Metrization Theorem........................ 71 5. Imbedding of Manifolds..........................
    [Show full text]
  • Sphere Vs. 0°/45° a Discussion of Instrument Geometries And
    Sphere vs. 0°/45° ® Author - Timothy Mouw Sphere vs. 0°/45° A discussion of instrument geometries and their areas of application Introduction When purchasing a spectrophotometer for color measurement, one of the choices that must be made is the geometry of the instrument; that is, whether to buy a spherical or 0°/45° instrument. In this article, we will attempt to provide some information to assist you in determining which type of instrument is best suited to your needs. In order to do this, we must first understand the differences between these instruments. Simplified schematics of instrument geometries We will begin by looking at some simple schematic drawings of the two different geometries, spherical and 0°/45°. Figure 1 shows a drawing of the geometry used in a 0°/45° instrument. The illumination of the sample is from 0° (90° from the sample surface). This means that the specular or gloss angle (the angle at which the light is directly reflected) is also 0°. The fiber optic pick-ups are located at 45° from the specular angle. Figure 1 X-Rite World Headquarters © 1995 X-Rite, Incorporated Doc# CA00015a.doc (616) 534-7663 Fax (616) 534-8960 September 15, 1995 Figure 2 shows a drawing of the geometry used in an 8° diffuse sphere instrument. The sphere wall is lined with a highly reflective white substance and the light source is located on the rear of the sphere wall. A baffle prevents the light source from directly illuminating the sample, thus providing diffuse illumination. The sample is viewed at 8° from perpendicular which means that the specular or gloss angle is also 8° from perpendicular.
    [Show full text]
  • General Topology
    General Topology Tom Leinster 2014{15 Contents A Topological spaces2 A1 Review of metric spaces.......................2 A2 The definition of topological space.................8 A3 Metrics versus topologies....................... 13 A4 Continuous maps........................... 17 A5 When are two spaces homeomorphic?................ 22 A6 Topological properties........................ 26 A7 Bases................................. 28 A8 Closure and interior......................... 31 A9 Subspaces (new spaces from old, 1)................. 35 A10 Products (new spaces from old, 2)................. 39 A11 Quotients (new spaces from old, 3)................. 43 A12 Review of ChapterA......................... 48 B Compactness 51 B1 The definition of compactness.................... 51 B2 Closed bounded intervals are compact............... 55 B3 Compactness and subspaces..................... 56 B4 Compactness and products..................... 58 B5 The compact subsets of Rn ..................... 59 B6 Compactness and quotients (and images)............. 61 B7 Compact metric spaces........................ 64 C Connectedness 68 C1 The definition of connectedness................... 68 C2 Connected subsets of the real line.................. 72 C3 Path-connectedness.......................... 76 C4 Connected-components and path-components........... 80 1 Chapter A Topological spaces A1 Review of metric spaces For the lecture of Thursday, 18 September 2014 Almost everything in this section should have been covered in Honours Analysis, with the possible exception of some of the examples. For that reason, this lecture is longer than usual. Definition A1.1 Let X be a set. A metric on X is a function d: X × X ! [0; 1) with the following three properties: • d(x; y) = 0 () x = y, for x; y 2 X; • d(x; y) + d(y; z) ≥ d(x; z) for all x; y; z 2 X (triangle inequality); • d(x; y) = d(y; x) for all x; y 2 X (symmetry).
    [Show full text]
  • Properties of Euclidean Space
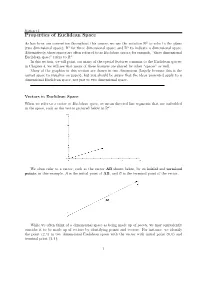
    Section 3.1 Properties of Euclidean Space As has been our convention throughout this course, we use the notation R2 to refer to the plane (two dimensional space); R3 for three dimensional space; and Rn to indicate n dimensional space. Alternatively, these spaces are often referred to as Euclidean spaces; for example, \three dimensional Euclidean space" refers to R3. In this section, we will point out many of the special features common to the Euclidean spaces; in Chapter 4, we will see that many of these features are shared by other \spaces" as well. Many of the graphics in this section are drawn in two dimensions (largely because this is the easiest space to visualize on paper), but you should be aware that the ideas presented apply to n dimensional Euclidean space, not just to two dimensional space. Vectors in Euclidean Space When we refer to a vector in Euclidean space, we mean directed line segments that are embedded in the space, such as the vector pictured below in R2: We often refer to a vector, such as the vector AB shown below, by its initial and terminal points; in this example, A is the initial point of AB, and B is the terminal point of the vector. While we often think of n dimensional space as being made up of points, we may equivalently consider it to be made up of vectors by identifying points and vectors. For instance, we identify the point (2; 1) in two dimensional Euclidean space with the vector with initial point (0; 0) and terminal point (2; 1): 1 Section 3.1 In this way, we think of n dimensional Euclidean space as being made up of n dimensional vectors.
    [Show full text]