Notes on Phase Seperation Chem 130A Fall 2002 Prof
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Phase Diagrams and Phase Separation
Phase Diagrams and Phase Separation Books MF Ashby and DA Jones, Engineering Materials Vol 2, Pergamon P Haasen, Physical Metallurgy, G Strobl, The Physics of Polymers, Springer Introduction Mixing two (or more) components together can lead to new properties: Metal alloys e.g. steel, bronze, brass…. Polymers e.g. rubber toughened systems. Can either get complete mixing on the atomic/molecular level, or phase separation. Phase Diagrams allow us to map out what happens under different conditions (specifically of concentration and temperature). Free Energy of Mixing Entropy of Mixing nA atoms of A nB atoms of B AM Donald 1 Phase Diagrams Total atoms N = nA + nB Then Smix = k ln W N! = k ln nA!nb! This can be rewritten in terms of concentrations of the two types of atoms: nA/N = cA nB/N = cB and using Stirling's approximation Smix = -Nk (cAln cA + cBln cB) / kN mix S AB0.5 This is a parabolic curve. There is always a positive entropy gain on mixing (note the logarithms are negative) – so that entropic considerations alone will lead to a homogeneous mixture. The infinite slope at cA=0 and 1 means that it is very hard to remove final few impurities from a mixture. AM Donald 2 Phase Diagrams This is the situation if no molecular interactions to lead to enthalpic contribution to the free energy (this corresponds to the athermal or ideal mixing case). Enthalpic Contribution Assume a coordination number Z. Within a mean field approximation there are 2 nAA bonds of A-A type = 1/2 NcAZcA = 1/2 NZcA nBB bonds of B-B type = 1/2 NcBZcB = 1/2 NZ(1- 2 cA) and nAB bonds of A-B type = NZcA(1-cA) where the factor 1/2 comes in to avoid double counting and cB = (1-cA). -

Suppression of Phase Separation in Lifepo4 Nanoparticles
Suppression of Phase Separation in LiFePO4 Nanoparticles During Battery Discharge Peng Bai,†,§ Daniel A. Cogswell† and Martin Z. Bazant*,†,‡ †Department of Chemical Engineering and ‡Department of Mathematics, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, Massachusetts 02139, USA §State Key Laboratory of Automotive Safety and Energy, Department of Automotive Engineering, Tsinghua University, Beijing 100084, P. R. China *Corresponding author: Dr. Martin Z. Bazant. Tel: (617)258-7039; Fax: (617)258-5766; Email: [email protected] August 8, 2011 ABSTRACT: Using a novel electrochemical phase-field model, we question the common belief that LixFePO4 nanoparticles separate into Li-rich and Li-poor phases during battery discharge. For small currents, spinodal decomposition or nucleation leads to moving phase boundaries. Above a critical current density (in the Tafel regime), the spinodal disappears, and particles fill homogeneously, which may explain the superior rate capability and long cycle life of nano-LiFePO4 cathodes. KEYWORDS: Li-ion battery, LiFePO4, phase-field model, Butler-Volmer equation, spinodal decomposition, intercalation waves. 1 Introduction. – LiFePO4-based electrochemical energy storage is one of the most promising developments for electric vehicle power systems and other high-rate applications such as power tools 2,3 and renewable energy storage. Nanoparticles of LiFePO4 have recently been used to demonstrate ultrafast battery discharge4 and high power density carbon pseudocapacitors.5 However, the -

Interval Mathematics Applied to Critical Point Transitions
Revista de Matematica:´ Teor´ıa y Aplicaciones 2005 12(1 & 2) : 29–44 cimpa – ucr – ccss issn: 1409-2433 interval mathematics applied to critical point transitions Benito A. Stradi∗ Received/Recibido: 16 Feb 2004 Abstract The determination of critical points of mixtures is important for both practical and theoretical reasons in the modeling of phase behavior, especially at high pressure. The equations that describe the behavior of complex mixtures near critical points are highly nonlinear and with multiplicity of solutions to the critical point equations. Interval arithmetic can be used to reliably locate all the critical points of a given mixture. The method also verifies the nonexistence of a critical point if a mixture of a given composition does not have one. This study uses an interval Newton/Generalized Bisection algorithm that provides a mathematical and computational guarantee that all mixture critical points are located. The technique is illustrated using several ex- ample problems. These problems involve cubic equation of state models; however, the technique is general purpose and can be applied in connection with other nonlinear problems. Keywords: Critical Points, Interval Analysis, Computational Methods. Resumen La determinaci´onde puntos cr´ıticosde mezclas es importante tanto por razones pr´acticascomo te´oricasen el modelamiento del comportamiento de fases, especial- mente a presiones altas. Las ecuaciones que describen el comportamiento de mezclas complejas cerca del punto cr´ıticoson significativamente no lineales y con multipli- cidad de soluciones para las ecuaciones del punto cr´ıtico. Aritm´eticade intervalos puede ser usada para localizar con confianza todos los puntos cr´ıticosde una mezcla dada. -

1504.05850V4.Pdf
Compact Stars in the QCD Phase Diagram IV (CSQCD IV) September 26-30, 2014, Prerow, Germany http://www.ift.uni.wroc.pl/˜csqcdiv Entropic and enthalpic phase transitions in high energy density nuclear matter Igor Iosilevskiy1,2 1 Joint Institute for High Temperatures (Russian Academy of Sciences), Izhorskaya Str. 13/2, 125412 Moscow, Russia 2 Moscow Institute of Physics and Technology (State Research University), Dolgoprudny, 141700, Moscow Region, Russia 1 Abstract Features of Gas-Liquid (GL) and Quark-Hadron (QH) phase transitions (PT) in dense nuclear matter are under discussion in comparison with their terrestrial coun- terparts, e.g. so-called ”plasma” PT in shock-compressed hydrogen, nitrogen etc. Both, GLPT and QHPT, when being represented in widely accepted temperature – baryonic chemical potential plane, are often considered as similar, i.e. amenable to one-to-one mapping by simple scaling. It is argued that this impression is illusive and that GLPT and QHPT belong to different classes: GLPT is typical enthalpic PT (Van-der-Waals-like) while QHPT (”deconfinement-driven”) is typical entropic PT. Subdivision of 1st-order fluid-fluid phase transitions into enthalpic and entropic subclasses was proposed in [arXiv:1403.8053]. Properties of enthalpic and entropic PTs differ significantly. Entropic PT is always internal part of more general and ex- tended thermodynamic anomaly – domains with abnormal (negative) sign for the set of (usually positive) second derivatives of thermodynamic potential, e.g. Gruneizen and thermal expansion and thermal pressure coefficients etc. Negative sign of these derivatives lead to violation of standard behavior and relative order for many iso-lines in P –V plane, e.g. -
![Arxiv:2010.01933V2 [Cond-Mat.Quant-Gas] 18 Feb 2021 Tigated in Refs](https://docslib.b-cdn.net/cover/8490/arxiv-2010-01933v2-cond-mat-quant-gas-18-feb-2021-tigated-in-refs-768490.webp)
Arxiv:2010.01933V2 [Cond-Mat.Quant-Gas] 18 Feb 2021 Tigated in Refs
Finite temperature spin dynamics of a two-dimensional Bose-Bose atomic mixture Arko Roy,1, ∗ Miki Ota,1, ∗ Alessio Recati,1, 2 and Franco Dalfovo1 1INO-CNR BEC Center and Universit`adi Trento, via Sommarive 14, I-38123 Trento, Italy 2Trento Institute for Fundamental Physics and Applications, INFN, 38123 Povo, Italy We examine the role of thermal fluctuations in uniform two-dimensional binary Bose mixtures of dilute ultracold atomic gases. We use a mean-field Hartree-Fock theory to derive analytical predictions for the miscible-immiscible transition. A nontrivial result of this theory is that a fully miscible phase at T = 0 may become unstable at T 6= 0, as a consequence of a divergent behaviour in the spin susceptibility. We test this prediction by performing numerical simulations with the Stochastic (Projected) Gross-Pitaevskii equation, which includes beyond mean-field effects. We calculate the equilibrium configurations at different temperatures and interaction strengths and we simulate spin oscillations produced by a weak external perturbation. Despite some qualitative agreement, the comparison between the two theories shows that the mean-field approximation is not able to properly describe the behavior of the two-dimensional mixture near the miscible-immiscible transition, as thermal fluctuations smoothen all sharp features both in the phase diagram and in spin dynamics, except for temperature well below the critical temperature for superfluidity. I. INTRODUCTION ing the Popov theory. It is then natural to ask whether such a phase-transition also exists in 2D. The study of phase-separation in two-component clas- It is worth stressing that, in 2D Bose gases, thermal sical fluids is of paramount importance and the role of fluctuations are much more important than in 3D, as they temperature can be rather nontrivial. -

Nucleation Initiated Spinodal Decomposition in a Polymerizing System Thein Yk U University of Akron Main Campus, [email protected]
The University of Akron IdeaExchange@UAkron College of Polymer Science and Polymer Engineering 5-1996 Nucleation Initiated Spinodal Decomposition in a Polymerizing System Thein yK u University of Akron Main Campus, [email protected] Jae Hyung Lee University of Akron Main Campus Please take a moment to share how this work helps you through this survey. Your feedback will be important as we plan further development of our repository. Follow this and additional works at: http://ideaexchange.uakron.edu/polymer_ideas Part of the Polymer Science Commons Recommended Citation Kyu, Thein nda Lee, Jae Hyung, "Nucleation Initiated Spinodal Decomposition in a Polymerizing System" (1996). College of Polymer Science and Polymer Engineering. 67. http://ideaexchange.uakron.edu/polymer_ideas/67 This Article is brought to you for free and open access by IdeaExchange@UAkron, the institutional repository of The nivU ersity of Akron in Akron, Ohio, USA. It has been accepted for inclusion in College of Polymer Science and Polymer Engineering by an authorized administrator of IdeaExchange@UAkron. For more information, please contact [email protected], [email protected]. VOLUME 76, NUMBER 20 PHYSICAL REVIEW LETTERS 13MAY 1996 Nucleation Initiated Spinodal Decomposition in a Polymerizing System Thein Kyu and Jae-Hyung Lee Institute of Polymer Engineering, The University of Akron, Akron, Ohio 44325 (Received 29 September 1995) Dynamics of phase separation in a polymerizing system, consisting of carboxyl terminated polybutadiene acrylonitrile/epoxy/methylene dianiline, was investigated by means of time-resolved light scattering. The initial length scale was found to decrease for some early periods of the reaction which has been explained in the context of nucleation initiated spinodal decomposition. -

Study of the LLE, VLE and VLLE of the Ternary System Water + 1-Butanol + Isoamyl Alcohol at 101.3 Kpa
View metadata, citation and similar papers at core.ac.uk brought to you by CORE Submitted to Journal of Chemical & Engineering Data provided by Repositorio Institucional de la Universidad de Alicante This document is confidential and is proprietary to the American Chemical Society and its authors. Do not copy or disclose without written permission. If you have received this item in error, notify the sender and delete all copies. Study of the LLE, VLE and VLLE of the ternary system water + 1-butanol + isoamyl alcohol at 101.3 kPa Journal: Journal of Chemical & Engineering Data Manuscript ID je-2018-00308r.R3 Manuscript Type: Article Date Submitted by the Author: 27-Aug-2018 Complete List of Authors: Saquete, María Dolores; Universitat d'Alacant, Chemical Engineering Font, Alicia; Universitat d'Alacant, Chemical Engineering Garcia-Cano, Jorge; Universitat d'Alacant, Chemical Engineering Blasco, Inmaculada; Universitat d'Alacant, Chemical Engineering ACS Paragon Plus Environment Page 1 of 21 Submitted to Journal of Chemical & Engineering Data 1 2 3 Study of the LLE, VLE and VLLE of the ternary system water + 4 1-butanol + isoamyl alcohol at 101.3 kPa 5 6 María Dolores Saquete, Alicia Font, Jorge García-Cano* and Inmaculada Blasco. 7 8 University of Alicante, P.O. Box 99, E-03080 Alicante, Spain 9 10 Abstract 11 12 In this work it has been determined experimentally the liquidliquid equilibrium of the 13 water + 1butanol + isoamyl alcohol system at 303.15K and 313.15K. The UNIQUAC, 14 NRTL and UNIFAC models have been employed to correlate and predict LLE and 15 16 compare them with the experimental data. -

Chapter 9: Other Topics in Phase Equilibria
Chapter 9: Other Topics in Phase Equilibria This chapter deals with relations that derive in cases of equilibrium between combinations of two co-existing phases other than vapour and liquid, i.e., liquid-liquid, solid-liquid, and solid- vapour. Each of these phase equilibria may be employed to overcome difficulties encountered in purification processes that exploit the difference in the volatilities of the components of a mixture, i.e., by vapour-liquid equilibria. As with the case of vapour-liquid equilibria, the objective is to derive relations that connect the compositions of the two co-existing phases as functions of temperature and pressure. 9.1 Liquid-liquid Equilibria (LLE) 9.1.1 LLE Phase Diagrams Unlike gases which are miscible in all proportions at low pressures, liquid solutions (binary or higher order) often display partial immiscibility at least over certain range of temperature, and composition. If one attempts to form a solution within that certain composition range the system splits spontaneously into two liquid phases each comprising a solution of different composition. Thus, in such situations the equilibrium state of the system is two phases of a fixed composition corresponding to a temperature. The compositions of two such phases, however, change with temperature. This typical phase behavior of such binary liquid-liquid systems is depicted in fig. 9.1a. The closed curve represents the region where the system exists Fig. 9.1 Phase diagrams for a binary liquid system showing partial immiscibility in two phases, while outside it the state is a homogenous single liquid phase. Take for example, the point P (or Q). -

Spinodal Lines and Equations of State: a Review
10 l Nuclear Engineering and Design 95 (1986) 297-314 297 North-Holland, Amsterdam SPINODAL LINES AND EQUATIONS OF STATE: A REVIEW John H. LIENHARD, N, SHAMSUNDAR and PaulO, BINEY * Heat Transfer/ Phase-Change Laboratory, Mechanical Engineering Department, University of Houston, Houston, TX 77004, USA The importance of knowing superheated liquid properties, and of locating the liquid spinodal line, is discussed, The measurement and prediction of the spinodal line, and the limits of isentropic pressure undershoot, are reviewed, Means are presented for formulating equations of state and fundamental equations to predict superheated liquid properties and spinodal limits, It is shown how the temperature dependence of surface tension can be used to verify p - v - T equations of state, or how this dependence can be predicted if the equation of state is known. 1. Scope methods for making simplified predictions of property information, which can be applied to the full range of Today's technology, with its emphasis on miniaturiz fluids - water, mercury, nitrogen, etc. [3-5]; and predic ing and intensifying thennal processes, steadily de tions of the depressurizations that might occur in ther mands higher heat fluxes and poses greater dangers of mohydraulic accidents. (See e.g. refs. [6,7].) sending liquids beyond their boiling points into the metastable, or superheated, state. This state poses the threat of serious thermohydraulic explosions. Yet we 2. The spinodal limit of liquid superheat know little about its thermal properties, and cannot predict process behavior after a liquid becomes super heated. Some of the practical situations that require a 2.1. The role of the equation of state in defining the spinodal line knowledge the limits of liquid superheat, and the physi cal properties of superheated liquids, include: - Thennohydraulic explosions as might occur in nuclear Fig. -

Definitions of Terms Relating to Phase Transitions of the Solid State
Definitions of terms relating to phase transitions of the solid state Citation for published version (APA): Clark, J. B., Hastie, J. W., Kihlborg, L. H. E., Metselaar, R., & Thackeray, M. M. (1994). Definitions of terms relating to phase transitions of the solid state. Pure and Applied Chemistry, 66(3), 577-594. https://doi.org/10.1351/pac199466030577 DOI: 10.1351/pac199466030577 Document status and date: Published: 01/01/1994 Document Version: Publisher’s PDF, also known as Version of Record (includes final page, issue and volume numbers) Please check the document version of this publication: • A submitted manuscript is the version of the article upon submission and before peer-review. There can be important differences between the submitted version and the official published version of record. People interested in the research are advised to contact the author for the final version of the publication, or visit the DOI to the publisher's website. • The final author version and the galley proof are versions of the publication after peer review. • The final published version features the final layout of the paper including the volume, issue and page numbers. Link to publication General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain • You may freely distribute the URL identifying the publication in the public portal. -

1000 J Mole Μa ( ) = 4,0001.09 TJ Mole Μb
3.012 PS 6 THERMODYANMICS SOLUTIONS 3.012 Issued: 11.28.05 Fall 2005 Due: THERMODYNAMICS 1. Building a binary phase diagram. Given below are data for a binary system of two materials A and B. The two components form three phases: an ideal liquid solution, and two solid phases α and β that exhibit regular solution behavior. Use the given thermodynamic data to answer the questions below. LIQUID PHASE: ALPHA PHASE: L J " J µo = "500 " 4.8T µo = #6000 ( A ) mole ( A ) mole L J " J µo = "1,000 "10T µo = #1,000 ( B ) mole ( B ) mole ! ! (T is temperature in K) Ω = 8,368 J/mole ! ! BETA PHASE: " J µo = #4,000 #1.09T ( A ) mole " J µo = #13,552 # 2.09T ( B ) mole ! (T is temperature in K) ! Ω = 7,000 J/mole a. Plot the free energy of L, alpha, and beta phases (overlaid on one plot) vs. XB at the following temperatures: 2000K, 1500K, 1000K, 925K, and 800K. For each plot, denote common tangents and drop vertical lines below the plot to a ‘composition bar’, as illustrated in the example plot below. For each graph, mark the stable phases as a function of XB in the composition bar below the graph, as illustrated in the example. 3.012 PS 6 1 of 18 12/11/05 EXAMPLE: 3.012 PS 6 2 of 18 12/11/05 3.012 PS 6 3 of 18 12/11/05 b. Using the free energy curves prepared in part (a), construct a qualitatively correct phase diagram for this system in the temperature range 800K – 2000K. -
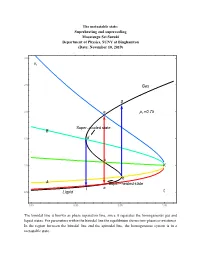
16.7 PT Superheating and Supercooling
The metastable state: Superheating and supercooling Masatsugu Sei Suzuki Department of Physics, SUNY at Binghamton (Date: November 10, 2019) 3.0 vr 2.5 Gas g 2.0 e pr 0.75 Super cooled state B 1.5 d c 1.0 K b A Super heated state l a 0.5 Liquid tr 0.85 0.90 0.95 1.00 The binodal line is known as phase separation line, since it separates the homogeneous gas and liquid states. For parameters within the binodal line the equilibrium shows two-phase co-existence. In the region between the binodal line and the spinodal line, the homogeneous system is in a metastable state. 3.0 vr 2.5 Gas p 0.70 r g pr 0.75 2.0 e pr 0.80 pr 0.85 B pr 0.90 1.5 d pr 0.95 c 1.0 K b A a l t 0.5 Liquid r 0.85 0.90 0.95 1.00 3.0 vr 2.5 Gas 2.0 g pr 0.80 e Super cooled state B 1.5 d c 1.0 K b A a l Super heated state 0.5 Liquid tr 0.85 0.90 0.95 1.00 e: the intersection of the ParametricPlot (denoted by black line) and the K-e line (binodal line) d: the intersection of the ParametricPlot (denoted by black line) and the K-d line (spinodal line) c: the intersection of the ParametricPlot (denoted by black line) and the K-c line b: the intersection of the ParametricPlot (denoted by black line) and the K-b line (spinodal line) a: the intersection of the ParametricPlot (denoted by black line) and the K-a line (binodal line) Point a: thermal equilibrium Point e: thermal equilibrium Point c: intermediate between the points a and b (temperature of point c is the same as that of points and e).