Atomic Momentum Distribution and Bose-Einstein Condensation in Liquid 4He Under Pressure
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Phase Diagrams and Phase Separation
Phase Diagrams and Phase Separation Books MF Ashby and DA Jones, Engineering Materials Vol 2, Pergamon P Haasen, Physical Metallurgy, G Strobl, The Physics of Polymers, Springer Introduction Mixing two (or more) components together can lead to new properties: Metal alloys e.g. steel, bronze, brass…. Polymers e.g. rubber toughened systems. Can either get complete mixing on the atomic/molecular level, or phase separation. Phase Diagrams allow us to map out what happens under different conditions (specifically of concentration and temperature). Free Energy of Mixing Entropy of Mixing nA atoms of A nB atoms of B AM Donald 1 Phase Diagrams Total atoms N = nA + nB Then Smix = k ln W N! = k ln nA!nb! This can be rewritten in terms of concentrations of the two types of atoms: nA/N = cA nB/N = cB and using Stirling's approximation Smix = -Nk (cAln cA + cBln cB) / kN mix S AB0.5 This is a parabolic curve. There is always a positive entropy gain on mixing (note the logarithms are negative) – so that entropic considerations alone will lead to a homogeneous mixture. The infinite slope at cA=0 and 1 means that it is very hard to remove final few impurities from a mixture. AM Donald 2 Phase Diagrams This is the situation if no molecular interactions to lead to enthalpic contribution to the free energy (this corresponds to the athermal or ideal mixing case). Enthalpic Contribution Assume a coordination number Z. Within a mean field approximation there are 2 nAA bonds of A-A type = 1/2 NcAZcA = 1/2 NZcA nBB bonds of B-B type = 1/2 NcBZcB = 1/2 NZ(1- 2 cA) and nAB bonds of A-B type = NZcA(1-cA) where the factor 1/2 comes in to avoid double counting and cB = (1-cA). -

Suppression of Phase Separation in Lifepo4 Nanoparticles
Suppression of Phase Separation in LiFePO4 Nanoparticles During Battery Discharge Peng Bai,†,§ Daniel A. Cogswell† and Martin Z. Bazant*,†,‡ †Department of Chemical Engineering and ‡Department of Mathematics, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, Massachusetts 02139, USA §State Key Laboratory of Automotive Safety and Energy, Department of Automotive Engineering, Tsinghua University, Beijing 100084, P. R. China *Corresponding author: Dr. Martin Z. Bazant. Tel: (617)258-7039; Fax: (617)258-5766; Email: [email protected] August 8, 2011 ABSTRACT: Using a novel electrochemical phase-field model, we question the common belief that LixFePO4 nanoparticles separate into Li-rich and Li-poor phases during battery discharge. For small currents, spinodal decomposition or nucleation leads to moving phase boundaries. Above a critical current density (in the Tafel regime), the spinodal disappears, and particles fill homogeneously, which may explain the superior rate capability and long cycle life of nano-LiFePO4 cathodes. KEYWORDS: Li-ion battery, LiFePO4, phase-field model, Butler-Volmer equation, spinodal decomposition, intercalation waves. 1 Introduction. – LiFePO4-based electrochemical energy storage is one of the most promising developments for electric vehicle power systems and other high-rate applications such as power tools 2,3 and renewable energy storage. Nanoparticles of LiFePO4 have recently been used to demonstrate ultrafast battery discharge4 and high power density carbon pseudocapacitors.5 However, the -

1504.05850V4.Pdf
Compact Stars in the QCD Phase Diagram IV (CSQCD IV) September 26-30, 2014, Prerow, Germany http://www.ift.uni.wroc.pl/˜csqcdiv Entropic and enthalpic phase transitions in high energy density nuclear matter Igor Iosilevskiy1,2 1 Joint Institute for High Temperatures (Russian Academy of Sciences), Izhorskaya Str. 13/2, 125412 Moscow, Russia 2 Moscow Institute of Physics and Technology (State Research University), Dolgoprudny, 141700, Moscow Region, Russia 1 Abstract Features of Gas-Liquid (GL) and Quark-Hadron (QH) phase transitions (PT) in dense nuclear matter are under discussion in comparison with their terrestrial coun- terparts, e.g. so-called ”plasma” PT in shock-compressed hydrogen, nitrogen etc. Both, GLPT and QHPT, when being represented in widely accepted temperature – baryonic chemical potential plane, are often considered as similar, i.e. amenable to one-to-one mapping by simple scaling. It is argued that this impression is illusive and that GLPT and QHPT belong to different classes: GLPT is typical enthalpic PT (Van-der-Waals-like) while QHPT (”deconfinement-driven”) is typical entropic PT. Subdivision of 1st-order fluid-fluid phase transitions into enthalpic and entropic subclasses was proposed in [arXiv:1403.8053]. Properties of enthalpic and entropic PTs differ significantly. Entropic PT is always internal part of more general and ex- tended thermodynamic anomaly – domains with abnormal (negative) sign for the set of (usually positive) second derivatives of thermodynamic potential, e.g. Gruneizen and thermal expansion and thermal pressure coefficients etc. Negative sign of these derivatives lead to violation of standard behavior and relative order for many iso-lines in P –V plane, e.g. -
![Arxiv:2010.01933V2 [Cond-Mat.Quant-Gas] 18 Feb 2021 Tigated in Refs](https://docslib.b-cdn.net/cover/8490/arxiv-2010-01933v2-cond-mat-quant-gas-18-feb-2021-tigated-in-refs-768490.webp)
Arxiv:2010.01933V2 [Cond-Mat.Quant-Gas] 18 Feb 2021 Tigated in Refs
Finite temperature spin dynamics of a two-dimensional Bose-Bose atomic mixture Arko Roy,1, ∗ Miki Ota,1, ∗ Alessio Recati,1, 2 and Franco Dalfovo1 1INO-CNR BEC Center and Universit`adi Trento, via Sommarive 14, I-38123 Trento, Italy 2Trento Institute for Fundamental Physics and Applications, INFN, 38123 Povo, Italy We examine the role of thermal fluctuations in uniform two-dimensional binary Bose mixtures of dilute ultracold atomic gases. We use a mean-field Hartree-Fock theory to derive analytical predictions for the miscible-immiscible transition. A nontrivial result of this theory is that a fully miscible phase at T = 0 may become unstable at T 6= 0, as a consequence of a divergent behaviour in the spin susceptibility. We test this prediction by performing numerical simulations with the Stochastic (Projected) Gross-Pitaevskii equation, which includes beyond mean-field effects. We calculate the equilibrium configurations at different temperatures and interaction strengths and we simulate spin oscillations produced by a weak external perturbation. Despite some qualitative agreement, the comparison between the two theories shows that the mean-field approximation is not able to properly describe the behavior of the two-dimensional mixture near the miscible-immiscible transition, as thermal fluctuations smoothen all sharp features both in the phase diagram and in spin dynamics, except for temperature well below the critical temperature for superfluidity. I. INTRODUCTION ing the Popov theory. It is then natural to ask whether such a phase-transition also exists in 2D. The study of phase-separation in two-component clas- It is worth stressing that, in 2D Bose gases, thermal sical fluids is of paramount importance and the role of fluctuations are much more important than in 3D, as they temperature can be rather nontrivial. -

Nucleation Initiated Spinodal Decomposition in a Polymerizing System Thein Yk U University of Akron Main Campus, [email protected]
The University of Akron IdeaExchange@UAkron College of Polymer Science and Polymer Engineering 5-1996 Nucleation Initiated Spinodal Decomposition in a Polymerizing System Thein yK u University of Akron Main Campus, [email protected] Jae Hyung Lee University of Akron Main Campus Please take a moment to share how this work helps you through this survey. Your feedback will be important as we plan further development of our repository. Follow this and additional works at: http://ideaexchange.uakron.edu/polymer_ideas Part of the Polymer Science Commons Recommended Citation Kyu, Thein nda Lee, Jae Hyung, "Nucleation Initiated Spinodal Decomposition in a Polymerizing System" (1996). College of Polymer Science and Polymer Engineering. 67. http://ideaexchange.uakron.edu/polymer_ideas/67 This Article is brought to you for free and open access by IdeaExchange@UAkron, the institutional repository of The nivU ersity of Akron in Akron, Ohio, USA. It has been accepted for inclusion in College of Polymer Science and Polymer Engineering by an authorized administrator of IdeaExchange@UAkron. For more information, please contact [email protected], [email protected]. VOLUME 76, NUMBER 20 PHYSICAL REVIEW LETTERS 13MAY 1996 Nucleation Initiated Spinodal Decomposition in a Polymerizing System Thein Kyu and Jae-Hyung Lee Institute of Polymer Engineering, The University of Akron, Akron, Ohio 44325 (Received 29 September 1995) Dynamics of phase separation in a polymerizing system, consisting of carboxyl terminated polybutadiene acrylonitrile/epoxy/methylene dianiline, was investigated by means of time-resolved light scattering. The initial length scale was found to decrease for some early periods of the reaction which has been explained in the context of nucleation initiated spinodal decomposition. -

Spinodal Lines and Equations of State: a Review
10 l Nuclear Engineering and Design 95 (1986) 297-314 297 North-Holland, Amsterdam SPINODAL LINES AND EQUATIONS OF STATE: A REVIEW John H. LIENHARD, N, SHAMSUNDAR and PaulO, BINEY * Heat Transfer/ Phase-Change Laboratory, Mechanical Engineering Department, University of Houston, Houston, TX 77004, USA The importance of knowing superheated liquid properties, and of locating the liquid spinodal line, is discussed, The measurement and prediction of the spinodal line, and the limits of isentropic pressure undershoot, are reviewed, Means are presented for formulating equations of state and fundamental equations to predict superheated liquid properties and spinodal limits, It is shown how the temperature dependence of surface tension can be used to verify p - v - T equations of state, or how this dependence can be predicted if the equation of state is known. 1. Scope methods for making simplified predictions of property information, which can be applied to the full range of Today's technology, with its emphasis on miniaturiz fluids - water, mercury, nitrogen, etc. [3-5]; and predic ing and intensifying thennal processes, steadily de tions of the depressurizations that might occur in ther mands higher heat fluxes and poses greater dangers of mohydraulic accidents. (See e.g. refs. [6,7].) sending liquids beyond their boiling points into the metastable, or superheated, state. This state poses the threat of serious thermohydraulic explosions. Yet we 2. The spinodal limit of liquid superheat know little about its thermal properties, and cannot predict process behavior after a liquid becomes super heated. Some of the practical situations that require a 2.1. The role of the equation of state in defining the spinodal line knowledge the limits of liquid superheat, and the physi cal properties of superheated liquids, include: - Thennohydraulic explosions as might occur in nuclear Fig. -

Notes on Phase Seperation Chem 130A Fall 2002 Prof
Notes on Phase Seperation Chem 130A Fall 2002 Prof. Groves Consider the process: Pure 1 + Pure 2 Æ Mixture of 1 and 2 We have previously derived the entropy of mixing for this process from statistical principles and found it to be: ∆ =− − Smix kN11ln X kN 2 ln X 2 where N1 and N2 are the number of molecules of type 1 and 2, respectively. We use k, the Boltzmann constant, since N1 and N2 are number of molecules. We could alternatively use R, the gas constant, if we chose to represent the number of molecules in terms of moles. X1 and X2 represent the mole fraction (e.g. X1 = N1 / (N1+N2)) of 1 and 2, respectively. If there are interactions between the two ∆ components, there will be a non-zero Hmix that we must consider. We can derive an expression ∆H = 2γ ∆ ∆ for Hmix using H of swapping one molecule of type 1, in pure type 1, with one molecule of type 2, in pure type 2 (see adjacent figure). We define γ as half of this ∆H of interchange. It is a differential interaction energy that tells us the energy difference between 1:1 and 2:2 interactions and 1:2 interactions. By defining 2γ = ∆H, γ represents the energy change associated with one molecule (note that two were involved in the swap). ∆ γ Now, to calculate Hmix from , we first consider 1 molecule of type 1 in the mixed system. For the moment we need not be concerned with whether or not they actually will mix, we just want ∆ to calculate Hmix as if they mix thoroughly. -

Phase Equilibria of Quasi-Ternary Systems Consisting of Multicomponent Polymers in a Binary Solvent Mixture IV
Polymer Journal, Vol. 18, No.4, pp 347-360 (1986) Phase Equilibria of Quasi-Ternary Systems Consisting of Multicomponent Polymers in a Binary Solvent Mixture IV. Spinodal Curve and Critical Solution Point Kenji KAMIDE and Shigenobu MATSUDA Fundamental Research Laboratory of Fiber and Fiber-Forming Polymers, Asahi Chemical Industry Company, Ltd., 11-7, Hacchonawate, Takatsuki, Osaka 569, Japan (Received October 28, 1985) ABSTRACT: An attempt was made to construct a quasi-ternary system cons1stmg of multicomponent polymers dissolved in binary solvent mixture (solvents I and 2) to derive the equations of spinodal and neutral equilibrium conditions and to clarify the effects of three thermodynamic interaction x-parameters between solvent I and solvent 2, solvent I and polymer, and solvent 2 and polymer(x 12, x13, and x23) and the weight-average degree of polymerization and the ratio of to the number-average degree of polymerization of the original polymer on the spinodal curve and the critical points (the critical concentration calculated from the above mentioned equations. The cloud point curve was also calculated indirectly from coexisting curve evaluated according to a method in our previous papers and constant (starting polymer volume fraction) line. The cross point of a constant line and a coexisting curve is a cloud point. The cloud point curve thus calculated was confirmed to coincide, as theory predicted with the spinodal curve, at the critical point. decreases with an increase in X12, x23, and and increases with an increase in x13 -
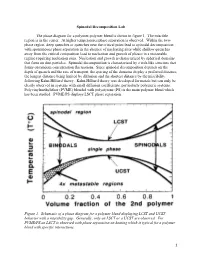
Spinodal Decomposition Lab.Pdf
Spinodal Decomposition Lab The phase diagram for a polymer-polymer blend is shown in figure 1. The miscible region is in the center. At higher temperatures phase separation is observed. Within the two- phase region, deep quenches or quenches near the critical point lead to spinodal decomposition with spontaneous phase separation in the absence of nucleating sites while shallow quenches away from the critical composition lead to nucleation and growth of phases in a metastable regime requiring nucleation sites. Nucleation and growth is characterized by spherical domains that form on dust particles. Spinodal decomposition is characterized by a web-like structure that forms on random concentration fluctuations. Since spinodal decomposition depends on the depth of quench and the rate of transport, the spacing of the domains display a preferred distance, the longest distance being limited by diffusion and the shortest distance by the miscibility following Kahn-Hilliard theory. Kahn-Hilliard theory was developed for metals but can only be clearly observed in systems with small diffusion coefficients, particularly polymeric systems. Polyvinylmethylether (PVME) blended with polystyrene (PS) is the main polymer blend which has been studied. PVME/PS displays LSCT phase separation. Figure 1. Schematic of a phase diagram for a polymer blend displaying LCST and UCST behavior with a miscibility gap. Generally, only an LSCT or a UCST are observed. For PVME/PS an LSCT is observed with phase separation on heating which is typical for a polymer blend with specific interactions. 1 ri is the degree of polymerization of the polymer component “i”, fi is the volume fraction of component “i”. -

Spinodal Decomposition of Atomic Nuclei
Philippe Chom&e/ Maria Coloana/^ and AHio Gnarnera^ ^ ^GANIL (DSM:/CEAJ.N2P3/CNRS) BP 5027, 14021 CAEN CedexJ^&ace ^LNS, Viale Andrea Dona Catania, Italy feArwary 7996 GANIL P 96 06 SPINODAL DECOMPOSITION OF ATOMIC NUCLEI Philippe Chomaz,1 Maria Colonna,1,2 and Alfio Guarnera1,2 ^GANIL (DSM/CEA,IN2P3/CNRS) BP 5027, 14021 CAEN Cedex,France 2LNS, Viale Andrea Doria Catania, Italy INTRODUCTION During the multifragmentation of atomic nuclei it seems that identical (or almost identical) initial conditions are leading to very different partitions of the system in in teraction. In such a case it is necessary to develop approaches that are able to describe the observed diversity of the final channels. On the other hand the multifragmentation being characterised by the formation of relatively large fragments, one may think that the mean field plays an important role to organise the system in nuclei. Indeed, the mean field (ie, the long range part of the bare nucleon-nucleon interaction) is at the origin of the cohesion of the clusters. Moreover, it has been shown that extentions of mean-field approaches including a Boltzmann-like collision term were providing excel lent descriptions of many aspects of heavy ion reactions around the Fermi energy (see for example ref.W and references therein). The problem with mean-field approaches is that they are unable to break sponta neously symmetries. Therefore, they cannot describe phenomena where bifurcations, instabilities or chaos occurs. However, since few years, many tests and studies have been reported showing that the stochastic extensions of mean-field approaches were good candidates for the description of such catastrophic processes. -

Spinodal Decomposition in the Binary Fe-Cr System
Spinodal decomposition in the binary Fe-Cr system Saeed Baghsheikhi Master’s degree project School of Industrial Engineering and Management Department of Materials Science and Engineering Royal Institute of Technology SE-100 44 Stockholm Sweden August 2009 ii Abstract Spinodal decomposition is a phase separation mechanism within the miscibility gap. Its importance in case of Fe-Cr system, the basis of the whole stainless steel family, stems from a phenomenon known as the “475oC embrittlement” which results in a ruin of mechanical properties of ferritic, martensitic and duplex stainless steels. This work is aimed at a better understanding of the phase separation process in the Fe-Cr system. Alloys of 10 to 55 wt.% Cr , each five percent, were homogenized to achieve fully ferritic microstructure and then isothermally aged at 400, 500 and 600oC for different periods of time ranging from 30min to 1500 hours. Hardness of both homogenized and aged samples were measured by the Vickers micro-hardness method and then selected samples were studied by means of Transmission Electron Microscopy (TEM). It was observed that hardness of homogenized samples increased monotonically with increasing Cr content up to 55 wt.% which can be attributed to solution hardening as well as higher hardness of pure chromium compared to pure iron. At 400oC no significant change in hardness was detected for aging up to 1500h, therefore we believe that phase separation effects at 400oC are very small up to this time. Sluggish kinetics is imputed to lower diffusion rate at lower temperatures. At 500oC even after 10h a noticeable change in hardness, for alloys containing 25 wt.% Cr and higher, was observed which indicates occurrence of phase separation. -

06. Thermodynamics of Phase Transitions II Gerhard Müller University of Rhode Island, [email protected] Creative Commons License
University of Rhode Island DigitalCommons@URI Equilibrium Statistical Physics Physics Course Materials 2015 06. Thermodynamics of Phase Transitions II Gerhard Müller University of Rhode Island, [email protected] Creative Commons License This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 4.0 License. Follow this and additional works at: http://digitalcommons.uri.edu/equilibrium_statistical_physics Abstract Part six of course materials for Statistical Physics I: PHY525, taught by Gerhard Müller at the University of Rhode Island. Documents will be updated periodically as more entries become presentable. Recommended Citation Müller, Gerhard, "06. Thermodynamics of Phase Transitions II" (2015). Equilibrium Statistical Physics. Paper 9. http://digitalcommons.uri.edu/equilibrium_statistical_physics/9 This Course Material is brought to you for free and open access by the Physics Course Materials at DigitalCommons@URI. It has been accepted for inclusion in Equilibrium Statistical Physics by an authorized administrator of DigitalCommons@URI. For more information, please contact [email protected]. Contents of this Document [ttc6] 6. Thermodynamics of Phase Transitions II • Van der Waals equation of state with coexistence curve. [tsl10] • Law of corresponding states. [tln30] • Maxwell construction. [tln31] • Gibbs and Helmholtz free energies of the van der Waals fluid at T < Tc. [tsl11] • Condensation and evaporation. [tln32] • Dieterici equation of state. [tex34] • Helium liquids. [tln33] • Phase diagram of 4He. [tsl13] • Phase diagram of 3He. [tsl14] • Exotic properties of helium II. [tln34] • Superconducting transition. [tln35] • Thermodynamics of a ferromagnet. [tsl5] • Structural transitions of iron. [tex53] • Latent heat and heat capacities at superconducting transition. [tex44] • Thermodynamics of the mean-field ferromagnet I. [tex45] • Thermodynamics of the mean-field ferromagnet II.