DOCSLIB.ORG

Finally: Resolution of D'alembert's Paradox

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Finally: Resolution of D'alembert's Paradox Finally: Resolution of d'Alembert's Paradox Johan Hoffman and Claes Johnson January 20, 2006 Abstract We propose a new resolution to d'Alembert's Paradox from 1752 com- paring the mathematical prediction of zero drag (resistance to motion) through an ideal (zero viscosity) incompressible fluid, with massive ob- servations of non-zero drag in fluids with very small viscosity, such as air and water. Our resolution is fundamentally different from the accepted resolution suggested by Prandtl in 1904 based on boundary layer effects of vanishing viscosity. We base our resolution on computational solution of the Euler equations describing ideal incompressible flow by noting that the zero drag potential solution considered by dAlembert, is unstable and instead a turbulent (approximate) solution develops with non-zero drag, even without boundary layer effects. We claim that our resolution is bet- ter than Prandtl's in the case of very small viscosity. 1 Introduction How wonderful that we have met with a paradox. Now we have some hope of making progress. (Nils Bohr) We present a new resolution of d'Alembert's Paradox from 1752 ([1]), which states that a body can move through an ideal (zero viscosity) incompressible fluid without any resistance (drag) to the motion. This statement is paradox- ical because all experience shows that motion through fluids with very small viscosity, such as air and water, meets a drag which is far from zero. Our res- olution is fundamentally different from the accepted resolution from 1904 by Ludwig Prandt ([2]), called the father of modern fluid mechanics, which builds on boundary layer effects from very small viscosity. We base our resolution on computational solution of the Euler equations de- scribing ideal incompressible fluid flow, which shows that the potential solution with zero drag considered by d'Alembert is unstable and instead a turbulent solution develops with non-zero drag. This solves the paradox in the origi- nal setting of d'Alembert and Euler, assuming the fluid to be ideal with zero viscosity, by showing that the zero drag potential solution cannot be realized physically, because it is unstable, and thus cannot be observed. We solve the Euler equations with a slip boundary condition at solid boundaries prescribing 1 the normal velocity to be zero but letting the tangential velocity be free, which means that no boundary layers are created. Nevertheless, a turbulent solution to the Euler equations with non-zero drag develops, starting from the poten- tial solution. Our resolution is thus completely different from Prandtl's and we claim that our resolution is more to the point for the very small viscosities met in a wide range of turbulent flows in aero- and hydro-dynamics. We also claim that our resolution is more satisfactory from a scientific point of view than Prandtl's, because we do no suggest that a very small cause (very small viscosity) can have a large effect (change the drag), as Prandtl does, which is close to saying that anything can happen from virtually nothing, and which can be very hard to either prove or disprove. We show instead that the potential solution is unstable and that a turbulent solution develops, even without influence from boundary layer effects of very small viscosity. We do not claim that boundary layer effects never influence the global flow, e.g. by separation, but we do claim that these effects may be small for very small viscosities, which fits with the observation that the so-called skin-friction tends to zero as the viscosity tends to zero. To solve the Euler equations numerically we use an adaptive finite element method with automatic control of the error in the drag ([8, 4, 5, 7, 9]), and we find that the computed drag is stable under mesh refinement. In [6] we also use a skin-friction boundary condition to model the effect of turbulent boundary layers, with zero skin-friction corresponding to a slip boundary condition. Let- ting the skin friction tend to zero, we obtain good agreement with experimental drag coefficients for varying viscosity (Reynolds number) including the so-called drag crisis occuring for very small viscosities ([10]). An outline of this note is as follows: We first recall the Euler equations for ideal incompressible fluid flow, and the stationary irrotational potentional solu- tion with zero drag considered by dAlembert. We then present computational results and point to basic features. Finally, we compare our new resolution of d'Alembert's Paradox with that of Prandtl, and leave to the reader to judge which resolution may be closer to the truth. 2 The Euler equations We consider the motion of an ideal incompressible fluid occupying a fixed volume Ω in R3 with boundary Γ. We want to find the fluid velocity u(x; t) and pressure p(x; t) for all points x = (x1; x2; x3) 2 Ω and time t > 0, assuming that the fluid flow through the boundary Γ and the initial velocity u(x; 0) are given. We assume that Γ is divided into a part Γ0 corresponding to a solid (inpenetrable) boundary, and a remaining part corresponding to inflow and outflow. The mathematical model for the motion of the fluid takes the form of the Euler equations formulated by Leonard Euler in 1755 ([11]) expressing conservation of momentum (Newton's second law) and conservation of mass, combined with 2 a boundary condition (g) and an initial condition (u0) for the velocity: u_ + (u · r)u + rp = 0; in Ω × I; r · u = 0; in Ω × I; (1) u · n = g; on Γ × I; u(·; 0) = u0; in Ω: Here n is the outward unit normal to Γ and the given boundary flow g satisfies RΓ g ds = 0 and g = 0 on Γ0. Requiring u · n = 0 on Γ0 corresponds to a slip boundary condition (bc) with the normal velocity vanishing, while the tangential velocity is free. This is to be compared to the no-slip bc u = 0 in Navier{Stokes equations (with non-zero viscosity ν > 0 including the term −ν∆u in the momentum equation), where also the tangential velocity is required to vanish reflecting that the fluid sticks to a solid boundary. Prandtl's resolution of the Paradox is connected to the no-slip bc, whereas we advocate that the slip bc is more relevant, in the case of very small viscosity. 3 Potential Flow around a Circular Cylinder Following d'Alembert we consider stationary (time-independent) potential flow around an (infinitely) long cylinder of diameter 1 oriented along the x3-axis and immersed in an ideal incompressible fluid filling R3 with velocity (1; 0; 0) at infinity. This models, for example, the flow of air around a tall cylindrical high- rise subject to a strong wind, or the flow of water around a pillar of a bridge in a strong current. The potential velocity is given as u = rφ, where φ satisfies Laplace's equation ∆φ = 0 outside the cylinder and appropriate conditions at infinity, that is, 1 φ(x1; x2; x3) = (r + ) cos(θ); (2) r where (x1; x2) = (r cos(θ); r sin(θ)) is expressed in polar coordinates (r; θ). Us- ing standard Calculus one verifies that u is irrotational, that is r × u = 0, since r × rφ = 0, and that (u; p) solves the Euler equations, where the pressure p is 1 2 determined by Bernoulli's Law stating that 2 juj + p is constant for stationary irrotational flow. In Fig. 1 we plot the streamlines of u in a section of the cylin- der, which are the curves followed by fluid particles, and the pressure. We notice that the potential flow (in each section) has one separation point at the back of the cylinder, where the flow separates from the cylinder boundary. We also notice that the both velocity and pressure are symmetric in the flow direction (x1-direction), which means that the drag of the cylinder is zero; the build up of pressure in front of the cylinder is balanced by the same strong pressure behind, and thus the drag is zero. The cylinder thus seems to be "pushed through the fluid” by the strong pressure behind, which of course is counter-intuitive and in fact is never observed in practice, where the pressure behind always is much lower than up front, with resulting non-zero drag. According to d'Alembert's potential solution there would be no wind load on a high-rise and no force on a 3 bridge pillar from a strong current, which is in contradiction with all practical experience. One can extend this result to flow around a body of arbitrary shape, since there is always a corresponding potential solution. We have thus met a scientific Paradox, which we have to resolve to save fluid mechanics as a mathematical science from collapse. But what do to? Evidently, something must be wrong with the potential solution, since it gives zero drag. But what? It cannot be Newton's second law or mass conservation. Figure 1: Potential solution of the Euler equations for flow past a circular cylin- der; colormap of the pressure (left) and streamlines together with a colormap of the magnitude of the velocity (right) . Prandtl in 1904 claimed that the Paradox is due to the assumption of zero viscosity. Prandtl stated that even if the viscosity is very small, it is not equal to zero, which means that one has to consider the Navier-Stokes equations with no-slip bc (instead of Eulers equations with slip bc), for which in a thin boundary layer close a solid boundary the fluid velocity will change quickly from zero at the boundary to the free stream value outside the layer.
Load more

Recommended publications
  • Glossary Physics (I-Introduction)
    1 Glossary Physics (I-introduction) - Efficiency: The percent of the work put into a machine that is converted into useful work output; = work done / energy used [-]. = eta In machines: The work output of any machine cannot exceed the work input (<=100%); in an ideal machine, where no energy is transformed into heat: work(input) = work(output), =100%. Energy: The property of a system that enables it to do work. Conservation o. E.: Energy cannot be created or destroyed; it may be transformed from one form into another, but the total amount of energy never changes. Equilibrium: The state of an object when not acted upon by a net force or net torque; an object in equilibrium may be at rest or moving at uniform velocity - not accelerating. Mechanical E.: The state of an object or system of objects for which any impressed forces cancels to zero and no acceleration occurs. Dynamic E.: Object is moving without experiencing acceleration. Static E.: Object is at rest.F Force: The influence that can cause an object to be accelerated or retarded; is always in the direction of the net force, hence a vector quantity; the four elementary forces are: Electromagnetic F.: Is an attraction or repulsion G, gravit. const.6.672E-11[Nm2/kg2] between electric charges: d, distance [m] 2 2 2 2 F = 1/(40) (q1q2/d ) [(CC/m )(Nm /C )] = [N] m,M, mass [kg] Gravitational F.: Is a mutual attraction between all masses: q, charge [As] [C] 2 2 2 2 F = GmM/d [Nm /kg kg 1/m ] = [N] 0, dielectric constant Strong F.: (nuclear force) Acts within the nuclei of atoms: 8.854E-12 [C2/Nm2] [F/m] 2 2 2 2 2 F = 1/(40) (e /d ) [(CC/m )(Nm /C )] = [N] , 3.14 [-] Weak F.: Manifests itself in special reactions among elementary e, 1.60210 E-19 [As] [C] particles, such as the reaction that occur in radioactive decay.
    [Show full text]
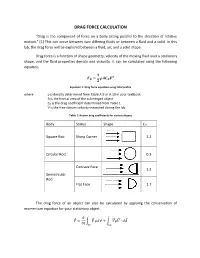
  • Drag Force Calculation
    DRAG FORCE CALCULATION “Drag is the component of force on a body acting parallel to the direction of relative motion.” [1] This can occur between two differing fluids or between a fluid and a solid. In this lab, the drag force will be explored between a fluid, air, and a solid shape. Drag force is a function of shape geometry, velocity of the moving fluid over a stationary shape, and the fluid properties density and viscosity. It can be calculated using the following equation, ퟏ 푭 = 흆푨푪 푽ퟐ 푫 ퟐ 푫 Equation 1: Drag force equation using total profile where ρ is density determined from Table A.9 or A.10 in your textbook A is the frontal area of the submerged object CD is the drag coefficient determined from Table 1 V is the free-stream velocity measured during the lab Table 1: Known drag coefficients for various shapes Body Status Shape CD Square Rod Sharp Corner 2.2 Circular Rod 0.3 Concave Face 1.2 Semicircular Rod Flat Face 1.7 The drag force of an object can also be calculated by applying the conservation of momentum equation for your stationary object. 휕 퐹⃗ = ∫ 푉⃗⃗ 휌푑∀ + ∫ 푉⃗⃗휌푉⃗⃗ ∙ 푑퐴⃗ 휕푡 퐶푉 퐶푆 Assuming steady flow, the equation reduces to 퐹⃗ = ∫ 푉⃗⃗휌푉⃗⃗ ∙ 푑퐴⃗ 퐶푆 The following frontal view of the duct is shown below. Integrating the velocity profile after the shape will allow calculation of drag force per unit span. Figure 1: Velocity profile after an inserted shape. Combining the previous equation with Figure 1, the following equation is obtained: 푊 퐷푓 = ∫ 휌푈푖(푈∞ − 푈푖)퐿푑푦 0 Simplifying the equation, you get: 20 퐷푓 = 휌퐿 ∑ 푈푖(푈∞ − 푈푖)훥푦 푖=1 Equation 2: Drag force equation using wake profile The pressure measurements can be converted into velocity using the Bernoulli’s equation as follows: 2Δ푃푖 푈푖 = √ 휌퐴푖푟 Be sure to remember that the manometers used are in W.C.
    [Show full text]
  • Chapter 4: Immersed Body Flow [Pp
    MECH 3492 Fluid Mechanics and Applications Univ. of Manitoba Fall Term, 2017 Chapter 4: Immersed Body Flow [pp. 445-459 (8e), or 374-386 (9e)] Dr. Bing-Chen Wang Dept. of Mechanical Engineering Univ. of Manitoba, Winnipeg, MB, R3T 5V6 When a viscous fluid flow passes a solid body (fully-immersed in the fluid), the body experiences a net force, F, which can be decomposed into two components: a drag force F , which is parallel to the flow direction, and • D a lift force F , which is perpendicular to the flow direction. • L The drag coefficient CD and lift coefficient CL are defined as follows: FD FL CD = 1 2 and CL = 1 2 , (112) 2 ρU A 2 ρU Ap respectively. Here, U is the free-stream velocity, A is the “wetted area” (total surface area in contact with fluid), and Ap is the “planform area” (maximum projected area of an object such as a wing). In the remainder of this section, we focus our attention on the drag forces. As discussed previously, there are two types of drag forces acting on a solid body immersed in a viscous flow: friction drag (also called “viscous drag”), due to the wall friction shear stress exerted on the • surface of a solid body; pressure drag (also called “form drag”), due to the difference in the pressure exerted on the front • and rear surfaces of a solid body. The friction drag and pressure drag on a finite immersed body are defined as FD,vis = τwdA and FD, pres = pdA , (113) ZA ZA Streamwise component respectively.
    [Show full text]
  • Brief History of the Early Development of Theoretical and Experimental Fluid Dynamics
    Brief History of the Early Development of Theoretical and Experimental Fluid Dynamics John D. Anderson Jr. Aeronautics Division, National Air and Space Museum, Smithsonian Institution, Washington, DC, USA 1 INTRODUCTION 1 Introduction 1 2 Early Greek Science: Aristotle and Archimedes 2 As you read these words, there are millions of modern engi- neering devices in operation that depend in part, or in total, 3 DA Vinci’s Fluid Dynamics 2 on the understanding of fluid dynamics – airplanes in flight, 4 The Velocity-Squared Law 3 ships at sea, automobiles on the road, mechanical biomedi- 5 Newton and the Sine-Squared Law 5 cal devices, and so on. In the modern world, we sometimes take these devices for granted. However, it is important to 6 Daniel Bernoulli and the Pressure-Velocity pause for a moment and realize that each of these machines Concept 7 is a miracle in modern engineering fluid dynamics wherein 7 Henri Pitot and the Invention of the Pitot Tube 9 many diverse fundamental laws of nature are harnessed and 8 The High Noon of Eighteenth Century Fluid combined in a useful fashion so as to produce a safe, efficient, Dynamics – Leonhard Euler and the Governing and effective machine. Indeed, the sight of an airplane flying Equations of Inviscid Fluid Motion 10 overhead typifies the laws of aerodynamics in action, and it 9 Inclusion of Friction in Theoretical Fluid is easy to forget that just two centuries ago, these laws were Dynamics: the Works of Navier and Stokes 11 so mysterious, unknown or misunderstood as to preclude a flying machine from even lifting off the ground; let alone 10 Osborne Reynolds: Understanding Turbulent successfully flying through the air.
    [Show full text]
  • In Classical Fluid Dynamics, a Boundary Layer Is the Layer I
    Atm S 547 Boundary Layer Meteorology Bretherton Lecture 1 Scope of Boundary Layer (BL) Meteorology (Garratt, Ch. 1) In classical fluid dynamics, a boundary layer is the layer in a nearly inviscid fluid next to a surface in which frictional drag associated with that surface is significant (term introduced by Prandtl, 1905). Such boundary layers can be laminar or turbulent, and are often only mm thick. In atmospheric science, a similar definition is useful. The atmospheric boundary layer (ABL, sometimes called P[lanetary] BL) is the layer of fluid directly above the Earth’s surface in which significant fluxes of momentum, heat and/or moisture are carried by turbulent motions whose horizontal and vertical scales are on the order of the boundary layer depth, and whose circulation timescale is a few hours or less (Garratt, p. 1). A similar definition works for the ocean. The complexity of this definition is due to several complications compared to classical aerodynamics. i) Surface heat exchange can lead to thermal convection ii) Moisture and effects on convection iii) Earth’s rotation iv) Complex surface characteristics and topography. BL is assumed to encompass surface-driven dry convection. Most workers (but not all) include shallow cumulus in BL, but deep precipitating cumuli are usually excluded from scope of BLM due to longer time for most air to recirculate back from clouds into contact with surface. Air-surface exchange BLM also traditionally includes the study of fluxes of heat, moisture and momentum between the atmosphere and the underlying surface, and how to characterize surfaces so as to predict these fluxes (roughness, thermal and moisture fluxes, radiative characteristics).
    [Show full text]
  • UNIT – 4 FORCES on IMMERSED BODIES Lecture-01
    1 UNIT – 4 FORCES ON IMMERSED BODIES Lecture-01 Forces on immersed bodies When a body is immersed in a real fluid, which is flowing at a uniform velocity U, the fluid will exert a force on the body. The total force (FR) can be resolved in two components: 1. Drag (FD): Component of the total force in the direction of motion of fluid. 2. Lift (FL): Component of the total force in the perpendicular direction of the motion of fluid. It occurs only when the axis of the body is inclined to the direction of fluid flow. If the axis of the body is parallel to the fluid flow, lift force will be zero. Expression for Drag & Lift Forces acting on the small elemental area dA are: i. Pressure force acting perpendicular to the surface i.e. p dA ii. Shear force acting along the tangential direction to the surface i.e. τ0dA (a) Drag force (FD) : Drag force on elemental area = p dAcosθ + τ0 dAcos(90 – θ = p dAosθ + τ0dAsinθ Hence Total drag (or profile drag) is given by, Where �� = ∫ � cos � �� + ∫�0 sin � �� = pressure drag or form drag, and ∫ � cos � �� = shear drag or friction drag or skin drag (b) Lift0 force (F ) : ∫ � sin � ��L Lift force on the elemental area = − p dAsinθ + τ0 dA sin(90 – θ = − p dAsiθ + τ0dAcosθ Hence, total lift is given by http://www.rgpvonline.com �� = ∫�0 cos � �� − ∫ p sin � �� 2 The drag & lift for a body moving in a fluid of density at a uniform velocity U are calculated mathematically as 2 � And �� = � � � 2 � Where A = projected area of the body or�� largest= � project� � area of the immersed body.
    [Show full text]
  • Chapter 5 Frictional Boundary Layers
    Chapter 5 Frictional boundary layers 5.1 The Ekman layer problem over a solid surface In this chapter we will take up the important question of the role of friction, especially in the case when the friction is relatively small (and we will have to find an objective measure of what we mean by small). As we noted in the last chapter, the no-slip boundary condition has to be satisfied no matter how small friction is but ignoring friction lowers the spatial order of the Navier Stokes equations and makes the satisfaction of the boundary condition impossible. What is the resolution of this fundamental perplexity? At the same time, the examination of this basic fluid mechanical question allows us to investigate a physical phenomenon of great importance to both meteorology and oceanography, the frictional boundary layer in a rotating fluid, called the Ekman Layer. The historical background of this development is very interesting, partly because of the fascinating people involved. Ekman (1874-1954) was a student of the great Norwegian meteorologist, Vilhelm Bjerknes, (himself the father of Jacques Bjerknes who did so much to understand the nature of the Southern Oscillation). Vilhelm Bjerknes, who was the first to seriously attempt to formulate meteorology as a problem in fluid mechanics, was a student of his own father Christian Bjerknes, the physicist who in turn worked with Hertz who was the first to demonstrate the correctness of Maxwell’s formulation of electrodynamics. So, we are part of a joined sequence of scientists going back to the great days of classical physics.
    [Show full text]
  • Chapter 4: Immersed Body Flow [Pp
    MECH 3492 Fluid Mechanics and Applications Univ. of Manitoba Fall Term, 2017 Chapter 4: Immersed Body Flow [pp. 445-459 (8e), or 374-386 (9e)] Dr. Bing-Chen Wang Dept. of Mechanical Engineering Univ. of Manitoba, Winnipeg, MB, R3T 5V6 When a viscous fluid flow passes a solid body (fully-immersed in the fluid), the body experiences a net force, F, which can be decomposed into two components: a drag force F , which is parallel to the flow direction, and • D a lift force F , which is perpendicular to the flow direction. • L The drag coefficient CD and lift coefficient CL are defined as follows: FD FL CD = 1 2 and CL = 1 2 , (112) 2 ρU A 2 ρU Ap respectively. Here, U is the free-stream velocity, A is the “wetted area” (total surface area in contact with fluid), and Ap is the “planform area” (maximum projected area of an object such as a wing). In the remainder of this section, we focus our attention on the drag forces. As discussed previously, there are two types of drag forces acting on a solid body immersed in a viscous flow: friction drag (also called “viscous drag”), due to the wall friction shear stress exerted on the • surface of a solid body; pressure drag (also called “form drag”), due to the difference in the pressure exerted on the front • and rear surfaces of a solid body. The friction drag and pressure drag on a finite immersed body are defined as FD,vis = τwdA and FD, pres = pdA , (113) ZA ZA Streamwise component respectively.
    [Show full text]
  • Hydraulics Manual Glossary G - 3
    Glossary G - 1 GLOSSARY OF HIGHWAY-RELATED DRAINAGE TERMS (Reprinted from the 1999 edition of the American Association of State Highway and Transportation Officials Model Drainage Manual) G.1 Introduction This Glossary is divided into three parts: · Introduction, · Glossary, and · References. It is not intended that all the terms in this Glossary be rigorously accurate or complete. Realistically, this is impossible. Depending on the circumstance, a particular term may have several meanings; this can never change. The primary purpose of this Glossary is to define the terms found in the Highway Drainage Guidelines and Model Drainage Manual in a manner that makes them easier to interpret and understand. A lesser purpose is to provide a compendium of terms that will be useful for both the novice as well as the more experienced hydraulics engineer. This Glossary may also help those who are unfamiliar with highway drainage design to become more understanding and appreciative of this complex science as well as facilitate communication between the highway hydraulics engineer and others. Where readily available, the source of a definition has been referenced. For clarity or format purposes, cited definitions may have some additional verbiage contained in double brackets [ ]. Conversely, three “dots” (...) are used to indicate where some parts of a cited definition were eliminated. Also, as might be expected, different sources were found to use different hyphenation and terminology practices for the same words. Insignificant changes in this regard were made to some cited references and elsewhere to gain uniformity for the terms contained in this Glossary: as an example, “groundwater” vice “ground-water” or “ground water,” and “cross section area” vice “cross-sectional area.” Cited definitions were taken primarily from two sources: W.B.
    [Show full text]
  • The Atmospheric Boundary Layer (ABL Or PBL)
    The Atmospheric Boundary Layer (ABL or PBL) • The layer of fluid directly above the Earth’s surface in which significant fluxes of momentum, heat and/or moisture are carried by turbulent motions whose horizontal and vertical scales are on the order of the boundary layer depth, and whose circulation timescale is a few hours or less (Garratt, p. 1). A similar definition works for the ocean. • The complexity of this definition is due to several complications compared to classical aerodynamics: i) Surface heat exchange can lead to thermal convection ii) Moisture and effects on convection iii) Earth’s rotation iv) Complex surface characteristics and topography. Atm S 547 Lecture 1, Slide 1 Sublayers of the atmospheric boundary layer Atm S 547 Lecture 1, Slide 2 Applications and Relevance of BLM i) Climate simulation and NWP ii) Air Pollution and Urban Meteorology iii) Agricultural meteorology iv) Aviation v) Remote Sensing vi) Military Atm S 547 Lecture 1, Slide 3 History of Boundary-Layer Meteorology 1900 – 1910 Development of laminar boundary layer theory for aerodynamics, starting with a seminal paper of Prandtl (1904). Ekman (1905,1906) develops his theory of laminar Ekman layer. 1910 – 1940 Taylor develops basic methods for examining and understanding turbulent mixing Mixing length theory, eddy diffusivity - von Karman, Prandtl, Lettau 1940 – 1950 Kolmogorov (1941) similarity theory of turbulence 1950 – 1960 Buoyancy effects on surface layer (Monin and Obuhkov, 1954). Early field experiments (e. g. Great Plains Expt. of 1953) capable of accurate direct turbulent flux measurements 1960 – 1970 The Golden Age of BLM. Accurate observations of a variety of boundary layer types, including convective, stable and trade- cumulus.
    [Show full text]
  • Boundary Layers
    1 I-campus project School-wide Program on Fluid Mechanics Modules on High Reynolds Number Flows K. P. Burr, T. R. Akylas & C. C. Mei CHAPTER TWO TWO-DIMENSIONAL LAMINAR BOUNDARY LAYERS 1 Introduction. When a viscous fluid flows along a fixed impermeable wall, or past the rigid surface of an immersed body, an essential condition is that the velocity at any point on the wall or other fixed surface is zero. The extent to which this condition modifies the general character of the flow depends upon the value of the viscosity. If the body is of streamlined shape and if the viscosity is small without being negligible, the modifying effect appears to be confined within narrow regions adjacent to the solid surfaces; these are called boundary layers. Within such layers the fluid velocity changes rapidly from zero to its main-stream value, and this may imply a steep gradient of shearing stress; as a consequence, not all the viscous terms in the equation of motion will be negligible, even though the viscosity, which they contain as a factor, is itself very small. A more precise criterion for the existence of a well-defined laminar boundary layer is that the Reynolds number should be large, though not so large as to imply a breakdown of the laminar flow. 2 Boundary Layer Governing Equations. In developing a mathematical theory of boundary layers, the first step is to show the existence, as the Reynolds number R tends to infinity, or the kinematic viscosity ν tends to zero, of a limiting form of the equations of motion, different from that obtained by putting ν = 0 in the first place.
    [Show full text]
  • List of Symbols
    List of Symbols a atmosphere speed of sound a exponent in approximate thrust formula ac aerodynamic center a acceleration vector a0 airfoil angle of attack for zero lift A aspect ratio A system matrix A aerodynamic force vector b span b exponent in approximate SFC formula c chord cd airfoil drag coefficient cl airfoil lift coefficient clα airfoil lift curve slope cmac airfoil pitching moment about the aerodynamic center cr root chord ct tip chord c¯ mean aerodynamic chord C specfic fuel consumption Cc corrected specfic fuel consumption CD drag coefficient CDf friction drag coefficient CDi induced drag coefficient CDw wave drag coefficient CD0 zero-lift drag coefficient Cf skin friction coefficient CF compressibility factor CL lift coefficient CLα lift curve slope CLmax maximum lift coefficient Cmac pitching moment about the aerodynamic center CT nondimensional thrust T Cm nondimensional thrust moment CW nondimensional weight d diameter det determinant D drag e Oswald’s efficiency factor E origin of ground axes system E aerodynamic efficiency or lift to drag ratio EO position vector f flap f factor f equivalent parasite area F distance factor FS stick force F force vector F F form factor g acceleration of gravity g acceleration of gravity vector gs acceleration of gravity at sea level g1 function in Mach number for drag divergence g2 function in Mach number for drag divergence H elevator hinge moment G time factor G elevator gearing h altitude above sea level ht altitude of the tropopause hH height of HT ac above wingc ¯ h˙ rate of climb 2 i unit vector iH horizontal
    [Show full text]