DOCSLIB.ORG

Conversion to Decibels

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Conversion to Decibels APPENDIX 1 CONVERSION TO DECIBELS Bels were named after Alexander Graham Bell. They were simply the logarithm of the ratio of power out and power in. The bel was too small to be useful; so the decibel quickly emerged. The definition of a decibel (dB) is contained in any radio engineer's handbook. It is where P is power, V is voltage, 0 is "out," and i is "in." In colloquial usage, dB are used to express any ratio. Decibels are just ten times the lOglO of that ratio. Some approximate dB conversions usually memorized by radar people are the following: Ratio dB Ratio dB I 0 20 13 1.25 I 100 20 1.6 2 10" IOn 2 3 ( 47T)3 33 3 5 Meters to nautical miles -33 4 6 Nmi to meters +33 5 7 Boltzmann's Constant (joules/oK) -228 6 8 Square degreeS in 47T steradians 46 7 8.5 Velocity of light (meters/sec) 85 8 9 (feet/sec) 90 9 9.5 (miles/sec) 53 10 10 174 APPENDIX 2 THE ELECTROMAGNETIC SPECTRUM Hertzian waves (3 kc - 3 X 106 MHz) t4+-----1.0------+-I·1 I HI\------"::......::::------Frequency in MHz--------~.1 1016 Cosmic rays I billionth of the electromagnetic spectrum Radar bands -----~ VLF LF MF HF VHF UHF SHF EHF .003 .03 .3 3 30 300 3000 30,000 t t Frequency (in megahertz) 3 X 105 3 X 106 I :Wavelength in meters I I 105 10,000 1000 100 1.0 .1 .01 .001 .0001 I I I I I Note: Laser radars are not included. They can range from about 107 MHz to 10/0 MHz. 175 APPENDIX 3 FOURIER SERIES AND TRANSFORMS* Working in the field of heat transfer in the early nineteenth century, Jean B. S. Fourier found that virtually all functions of time, particularly repetitive ones, could be described in a series of sine and cosine waves of various frequencies and amplitudes. His work has been described as one of the most elegant developments in modern mathematics. Whatever its stature for the world, the benefits for the radar engineer are epic. FOURIER SERIES The statement for the Fourier series is that any wave may be broken down into the sum of sines and cosines of various amplitudes and frequencies. In mathematical notation 1 f(t) = "2 ao + al cos wt + a2 cos 2wt + + b l sin wt + b2 sin 2wt + .... (1) f(t) is a function of time here (it does not have to be), and the aj and bi are constants that are to be found in order to make the expression on the right equal to f(t); ~ ao is the de component of the function, if any. The next step is to find a way to evaluate the aj and the bi . To do this, we use the orthogonality of the sine and cosine function, which is that the value of their cross products integrated from zero to 27T is zero. Furthermore, the sine and cosine each integrated from zero to 27T is zero. These integrations are easy to check by referring to a table of integrals; they are (27T (27T Jo sin rnx dx = 0 Jo cos nx dx = 0 J:7T cos rnx cos nx dx = 0 (2) * This presentation uses the approach taken by H. H. Skilling in Electrical Engineering Circuits (New York: Wiley, 1957), chaps. 14, 15. 176 Appendix III 177 Also {27T {27T J0 sin mx sin nx dx = 0 Jo cos mx cox nx dx = 0 (3) But {27T (27T ) Jo (sin mx)2 dx = 1T Jo (cos mx)" dx = 1T (4) Let us pick a coefficient to solve for, say, a2. Multiply through equation (1) by cos 2wt, then multiply both sides by d(wt) and integrate. We get 2IT . f21T I fo J(t) cos 2wt d(wt) = 0 2 ao cos 2wt d(wt) + 21T f21T fo al cos wt cos 2wt d(wt) + ... + 0 bl sin wt cos 2wt d(wt) + We can see by inspection that most of these integrals are zero. On the right side of the equation, the first and second terms are zero. But the third term equals a21T. In fact, all other terms written down and all implicit terms are zero, giving finally 21T fo J(t) cos 2wt d(wt) = a2 1T (5) and 1 f21T a2 = - J(t) cos 2wt d(wt) (6) 1T 0 Because we do know J(t), we can find a2, even if we have to do it by numerical integration on a home computer or programmable calculator. And because we did this in general, we can now generalize to 1 f21T an = - J(t) cos nwt d(wt) (7) 1T 0 and, after multiplying through by a sine function 1 f27T bn = - J(t) sin nwt d(wt) (8) 1T 0 Equation (1) is the Fourier series, but it can be rewritten for brevity as 178 Radar Principles for the Non-Specialist 1 x J(t) = "2 ao + ];1 (am COS mwt + bm sin mwt) (9) Writing down a function and evaluating it is the essence of tedium, but by astute observation, the process can be shortened. Some of the waves we are interested in in radar are not too difficult. For example, a periodic square wave (Figure A3.1) has no even harmonics. It is just an infinite sum of odd harmonics with ever-increasing frequencies and ever-decreasing coefficients. The answer for a square wave is 4(. 1. 1. ) J (w) = -; sm wt + 3" sm 3wt + "5 sm 5wt + ... (10) FOURIER TRANSFORMS To arrive at the Fourier transforms, we must take a few preliminary steps. The first is to restate equation (1) in exponential form. We can do this by substituting for cosines and sines their identities, which are We can now write the Fourier series as (11) f +1 on n_n I ;~ J U U U I I I I 0 'TT 2'TT 2 3 4 5 6 ~ wt Hannonics of fundamental FIGURE A3.1 A square wave and its Fourier spectrum Appendix III 179 or The coefficients are related in this way (12) and the coefficients can be found from the integral I J,27T A = - Jet) e-jnwt d(wt) (13) n 27T 0 j(t) is the function of time to be expressed as a Fourier series and the integer n can now be positive, negative, or zero. The integral (13) is used just like equations (7) and (8) to obtain coefficients. It is more efficient because there is only a single integral, and it is much more readily integrated. Equation (13) can be derived from equations (7) and (8) through the use of Euler's theorem. By matching their infinite series, Euler showed that ejO< = cos a + j sin a Consider now a square wave, as in Figure A3.2, where we have made the width ofthe pulse equal the interpulse period divided by a constant. We solve for the coefficients with 1 J7Tlk A = - e-jnJC dx n 27T -rrlk T ~I +1 I- T - k 0 'IT 'IT -'IT 0 'IT • X 2 2 FIGURE A3.2 Another square wave 180 Radar Principles for the Non-Specialist e 0 /k de 1 1 sin (mr/k) .. I·k h f lor n = , Ao = 1 an lor n r 0, An = k n1T/ k ' glvmg a spectrum let at 0 Figure A3.3. The spectrum of Figure A3.3 has an envelope of the sin xix shape, which we know to be the Fourier transform of a single pulse and the larger the value of k, the closer the spectral lines are together and the more closely a continuous function is replicated. No matter how large we make k, however, this envelope is still caused by lines of discrete frequencies. How can those discrete frequencies exist? They exist because the time function they are describing goes on forever. If it starts and stops, there will of necessity be a continuum offrequen­ cies, that is, the An will blend. There will be an An for every incremental distance along the frequency axis, not just at discrete points. The An will become a function offrequency, say, g(w), and the integer n will become an w on the other side of the equation. The limits of integration must be extended to find the stopping point of the time funrtiof'. These changes give us g(w) = -1 IX f(t) e-}wt dt (14) 21T -x for the frequency function and, by symmetry f(t) = J:x g(w) e}wt dw (15) These are called the Fourier integral equations or the Fourier transform pair. In this book, antenna illumination functions are transformed into far-field antenna patterns and waveform time functions into their spectra. In both these actions, equations (14) and (15) are applicable. Let us do an example with a single square pulse of height 1 and duration T 1 IT/2 . g(w) = - le-}wt dt (16) 21T -T/2 sinn1Tlk __-./ n1Tlk / \f-i k=4 /~2-'2 k FIGURE A3.3 Another spectrum of a square wave Appendix III 181 T 1(1) .----If----...-- + 1 T T o +2: 2 T T T T T T FIGURE A3.4 A single pulse and its Fourier transform (17) . T Sill w 1 . T T 2 = - Sill W - = - --- (18) TrW 2 2Tr T w- 2 The results are shown in Figure A3.4. Note that if e were substituted for T and 0 for w, the result would be for an antenna pattern (close to the boresight where sin o ~ 0).
Load more

Recommended publications
  • Db Math Marco Zennaro Ermanno Pietrosemoli Goals
    dB Math Marco Zennaro Ermanno Pietrosemoli Goals ‣ Electromagnetic waves carry power measured in milliwatts. ‣ Decibels (dB) use a relative logarithmic relationship to reduce multiplication to simple addition. ‣ You can simplify common radio calculations by using dBm instead of mW, and dB to represent variations of power. ‣ It is simpler to solve radio calculations in your head by using dB. 2 Power ‣ Any electromagnetic wave carries energy - we can feel that when we enjoy (or suffer from) the warmth of the sun. The amount of energy received in a certain amount of time is called power. ‣ The electric field is measured in V/m (volts per meter), the power contained within it is proportional to the square of the electric field: 2 P ~ E ‣ The unit of power is the watt (W). For wireless work, the milliwatt (mW) is usually a more convenient unit. 3 Gain and Loss ‣ If the amplitude of an electromagnetic wave increases, its power increases. This increase in power is called a gain. ‣ If the amplitude decreases, its power decreases. This decrease in power is called a loss. ‣ When designing communication links, you try to maximize the gains while minimizing any losses. 4 Intro to dB ‣ Decibels are a relative measurement unit unlike the absolute measurement of milliwatts. ‣ The decibel (dB) is 10 times the decimal logarithm of the ratio between two values of a variable. The calculation of decibels uses a logarithm to allow very large or very small relations to be represented with a conveniently small number. ‣ On the logarithmic scale, the reference cannot be zero because the log of zero does not exist! 5 Why do we use dB? ‣ Power does not fade in a linear manner, but inversely as the square of the distance.
    [Show full text]
  • Decibels, Phons, and Sones
    Decibels, Phons, and Sones The rate at which sound energy reaches a Table 1: deciBel Ratings of Several Sounds given cross-sectional area is known as the Sound Source Intensity deciBel sound intensity. There is an abnormally Weakest Sound Heard 1 x 10-12 W/m2 0.0 large range of intensities over which Rustling Leaves 1 x 10-11 W/m2 10.0 humans can hear. Given the large range, it Quiet Library 1 x 10-9 W/m2 30.0 is common to express the sound intensity Average Home 1 x 10-7 W/m2 50.0 using a logarithmic scale known as the Normal Conversation 1 x 10-6 W/m2 60.0 decibel scale. By measuring the intensity -4 2 level of a given sound with a meter, the Phone Dial Tone 1 x 10 W/m 80.0 -3 2 deciBel rating can be determined. Truck Traffic 1 x 10 W/m 90.0 Intensity values and decibel ratings for Chainsaw, 1 m away 1 x 10-1 W/m2 110.0 several sound sources listed in Table 1. The decibel scale and the intensity values it is based on is an objective measure of a sound. While intensities and deciBels (dB) are measurable, the loudness of a sound is subjective. Sound loudness varies from person to person. Furthermore, sounds with equal intensities but different frequencies are perceived by the same person to have unequal loudness. For instance, a 60 dB sound with a frequency of 1000 Hz sounds louder than a 60 dB sound with a frequency of 500 Hz.
    [Show full text]
  • Guide for the Use of the International System of Units (SI)
    Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S.
    [Show full text]
  • 4.1 – Radian and Degree Measure
    4.1 { Radian and Degree Measure Accelerated Pre-Calculus Mr. Niedert Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 1 / 27 2 Radian Measure 3 Degree Measure 4 Applications 4.1 { Radian and Degree Measure 1 Angles Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 2 / 27 3 Degree Measure 4 Applications 4.1 { Radian and Degree Measure 1 Angles 2 Radian Measure Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 2 / 27 4 Applications 4.1 { Radian and Degree Measure 1 Angles 2 Radian Measure 3 Degree Measure Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 2 / 27 4.1 { Radian and Degree Measure 1 Angles 2 Radian Measure 3 Degree Measure 4 Applications Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 2 / 27 The starting position of the ray is the initial side of the angle. The position after the rotation is the terminal side of the angle. The vertex of the angle is the endpoint of the ray. Angles An angle is determine by rotating a ray about it endpoint. Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 3 / 27 The position after the rotation is the terminal side of the angle. The vertex of the angle is the endpoint of the ray. Angles An angle is determine by rotating a ray about it endpoint. The starting position of the ray is the initial side of the angle. Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 3 / 27 The vertex of the angle is the endpoint of the ray.
    [Show full text]
  • The Decibel Scale R.C
    The Decibel Scale R.C. Maher Fall 2014 It is often convenient to compare two quantities in an audio system using a proportionality ratio. For example, if a linear amplifier produces 2 volts (V) output amplitude when its input amplitude is 100 millivolts (mV), the voltage gain is expressed as the ratio of output/input: 2V/100mV = 20. As long as the two quantities being compared have the same units--volts in this case--the proportionality ratio is dimensionless. If the proportionality ratios of interest end up being very large or very small, such as 2x105 and 2.5x10-4, manipulating and interpreting the results can become rather unwieldy. In this situation it can be helpful to compress the numerical range by taking the logarithm of the ratio. It is customary to use a base-10 logarithm for this purpose. For example, 5 log10(2x10 ) = 5 + log10(2) = 5.301 and -4 log10(2.5x10 ) = -4 + log10(2.5) = -3.602 If the quantities in the proportionality ratio both have the units of power (e.g., 2 watts), or intensity (watts/m ), then the base-10 logarithm log10(power1/power0) is expressed with the unit bel (symbol: B), in honor of Alexander Graham Bell (1847 -1922). The decibel is a unit representing one tenth (deci-) of a bel. Therefore, a figure reported in decibels is ten times the value reported in bels. The expression for a proportionality ratio expressed in decibel units (symbol dB) is: 10 푝표푤푒푟1 10 Common Usage 푑퐵 ≡ ∙ 푙표푔 �푝표푤푒푟0� The power dissipated in a resistance R ohms can be expressed as V2/R, where V is the voltage across the resistor.
    [Show full text]
  • Relationships of the SI Derived Units with Special Names and Symbols and the SI Base Units
    Relationships of the SI derived units with special names and symbols and the SI base units Derived units SI BASE UNITS without special SI DERIVED UNITS WITH SPECIAL NAMES AND SYMBOLS names Solid lines indicate multiplication, broken lines indicate division kilogram kg newton (kg·m/s2) pascal (N/m2) gray (J/kg) sievert (J/kg) 3 N Pa Gy Sv MASS m FORCE PRESSURE, ABSORBED DOSE VOLUME STRESS DOSE EQUIVALENT meter m 2 m joule (N·m) watt (J/s) becquerel (1/s) hertz (1/s) LENGTH J W Bq Hz AREA ENERGY, WORK, POWER, ACTIVITY FREQUENCY second QUANTITY OF HEAT HEAT FLOW RATE (OF A RADIONUCLIDE) s m/s TIME VELOCITY katal (mol/s) weber (V·s) henry (Wb/A) tesla (Wb/m2) kat Wb H T 2 mole m/s CATALYTIC MAGNETIC INDUCTANCE MAGNETIC mol ACTIVITY FLUX FLUX DENSITY ACCELERATION AMOUNT OF SUBSTANCE coulomb (A·s) volt (W/A) C V ampere A ELECTRIC POTENTIAL, CHARGE ELECTROMOTIVE ELECTRIC CURRENT FORCE degree (K) farad (C/V) ohm (V/A) siemens (1/W) kelvin Celsius °C F W S K CELSIUS CAPACITANCE RESISTANCE CONDUCTANCE THERMODYNAMIC TEMPERATURE TEMPERATURE t/°C = T /K – 273.15 candela 2 steradian radian cd lux (lm/m ) lumen (cd·sr) 2 2 (m/m = 1) lx lm sr (m /m = 1) rad LUMINOUS INTENSITY ILLUMINANCE LUMINOUS SOLID ANGLE PLANE ANGLE FLUX The diagram above shows graphically how the 22 SI derived units with special names and symbols are related to the seven SI base units. In the first column, the symbols of the SI base units are shown in rectangles, with the name of the unit shown toward the upper left of the rectangle and the name of the associated base quantity shown in italic type below the rectangle.
    [Show full text]
  • Draft 9Th Edition of the SI Brochure
    —————————————————————————— Bureau International des Poids et Mesures The International System of Units (SI) 9th edition 2019 —————————————————— 2 ▪ Draft of the ninth SI Brochure, 5 February 2018 The BIPM and the Metre Convention The International Bureau of Weights and Measures (BIPM) was set up by the Metre As of 20 May 2019, fifty Convention signed in Paris on 20 May 1875 by seventeen States during the final session of nine States were Members of this Convention: the diplomatic Conference of the Metre. This Convention was amended in 1921. Argentina, Australia, 2 Austria, Belgium, Brazil, The BIPM has its headquarters near Paris, in the grounds (43 520 m ) of the Pavillon de Bulgaria, Canada, Chile, Breteuil (Parc de Saint-Cloud) placed at its disposal by the French Government; its upkeep China, Colombia, Croatia, is financed jointly by the Member States of the Metre Convention. Czech Republic, Denmark, Egypt, Finland, The task of the BIPM is to ensure worldwide unification of measurements; its function is France, Germany, Greece, Hungary, India, Indonesia, thus to: Iran (Islamic Rep. of), • establish fundamental standards and scales for the measurement of the principal physical Iraq, Ireland, Israel, Italy, Japan, Kazakhstan, quantities and maintain the international prototypes; Kenya, Korea (Republic • carry out comparisons of national and international standards; of), Lithuania, Malaysia, • ensure the coordination of corresponding measurement techniques; Mexico, Montenegro, Netherlands, New • carry out and coordinate measurements of the fundamental physical constants relevant Zealand, Norway, to these activities. Pakistan, Poland, Portugal, Romania, The BIPM operates under the exclusive supervision of the International Committee for Russian Federation, Saudi Weights and Measures (CIPM) which itself comes under the authority of the General Arabia, Serbia, Singapore, Slovakia, Slovenia, South Conference on Weights and Measures (CGPM) and reports to it on the work accomplished Africa, Spain, Sweden, by the BIPM.
    [Show full text]
  • The International System of Units (SI)
    NAT'L INST. OF STAND & TECH NIST National Institute of Standards and Technology Technology Administration, U.S. Department of Commerce NIST Special Publication 330 2001 Edition The International System of Units (SI) 4. Barry N. Taylor, Editor r A o o L57 330 2oOI rhe National Institute of Standards and Technology was established in 1988 by Congress to "assist industry in the development of technology . needed to improve product quality, to modernize manufacturing processes, to ensure product reliability . and to facilitate rapid commercialization ... of products based on new scientific discoveries." NIST, originally founded as the National Bureau of Standards in 1901, works to strengthen U.S. industry's competitiveness; advance science and engineering; and improve public health, safety, and the environment. One of the agency's basic functions is to develop, maintain, and retain custody of the national standards of measurement, and provide the means and methods for comparing standards used in science, engineering, manufacturing, commerce, industry, and education with the standards adopted or recognized by the Federal Government. As an agency of the U.S. Commerce Department's Technology Administration, NIST conducts basic and applied research in the physical sciences and engineering, and develops measurement techniques, test methods, standards, and related services. The Institute does generic and precompetitive work on new and advanced technologies. NIST's research facilities are located at Gaithersburg, MD 20899, and at Boulder, CO 80303.
    [Show full text]
  • Angles Are Inherently Neither Length Ratios Nor Dimensionless
    Angles are inherently neither length ratios nor dimensionless Paul Quinceya, Peter J Mohrb and William D Phillipsb a National Physical Laboratory, Hampton Road, Teddington, TW11 0LW, United Kingdom b National Institute of Standards and Technology, Gaithersburg, MD 20899, USA Accepted for publication by Metrologia, 7 June 2019 Abstract The status of angles within The International System of Units (SI) has long been a source of controversy and confusion. We address one specific but crucial issue, putting the case that the idea of angles necessarily being length ratios, and hence dimensionless, is not valid. By making a clear distinction between the definition of a quantity and the process of making a measurement of that quantity, we show that the usual arguments for angles being length ratios are problematic. An appreciation of this point should clear away a major obstacle preventing a more proper treatment of the angle problem. Introduction One way to point out the odd status of angles within the SI is as follows: angle is measurable with a scale, on a protractor, in analogy to the way length is measureable with a ruler. It can therefore have units that are chosen by the user. This simple point is reinforced by the fact that multiple units for angle are used in practice. Angle measurements often use the degree, while the radian, which is used in mathematics and theoretical physics, is the SI unit. Other units, such as the grad, are used in specialised areas. And yet angle is treated as being dimensionless in the SI, a status usually applied only to quantities that are simply counted, like the number of molecules in a container, or quantities that are clearly a ratio of two values of the same quantity, such as refractive index.
    [Show full text]
  • Intensity of Sound
    01/02 Intensity - 1 INTENSITY OF SOUND The objectives of this experiment are: • To understand the concept of sound intensity and how it is measured. • To learn how to operate a Sound Level Meter APPARATUS: Radio Shack Sound Level Meter, meterstick, function generator, headphones. INTRODUCTION Sound energy is conveyed to our ears (or instruments) by means of a wave motion through some medium (gas, liquid, or solid). At any given point in the medium the energy content of the wave disturbance varies as the square of the amplitude of the wave motion. That is, if the amplitude of the oscillation is doubled the energy of the wave motion is quadrupled. The common method in gauging this energy transport is to measure the rate at which energy is passing a certain point. This concept involves sound intensity. Consider an area that is normal to the direction of the sound waves. If the area is a unit, namely one square meter, the quantity of sound energy expressed in Joules that passes through the unit area in one second defines the sound intensity. Recall the time rate of energy transfer is called "power". Thus, sound intensity is the power per square meter. The common unit of power is the watt ( 1w = 1 Joules/s). Normally, sound intensity is measured as a relative ratio to some standard intensity, Io. The response of the human ear to sound waves follows closely to a logarithmic function of the form R = k log I , where R is the response to a sound that has an intensity of I, and k is a constant of proportionality .
    [Show full text]
  • CTS-Prep Workshop II Ohm's Law, Impedance and Decibels Italy, April
    CTS-Prep Workshop II Ohm’s Law, Impedance and Decibels Italy, April 2020 Jose Mozota CTS, CTS-I 1 © 2017 AVIXA Goals • Review Ohm’s Law - Calculate V, I, R and P - Understand Bus Power in AV systems • Calculate Speaker Systems Impedance (Z) • Understand Impedance matching with amplifiers • Review the concept of Decibel • Understand Decibel calculations • Review Speaker configurations 2 © 2017 AVIXA Circuits Circuits have: - Source - Load - Conductor 3 © 2017 AVIXA Ohm's Law V = I * R V (voltage) - volts I (current) - amperes R (resistance) - ohms 4 © 2017 AVIXA Introduction to Ohm's Law • Expresses the relationships between Voltage (V), Current (I) and Resistance (R) in an electrical circuit V = I * R • Helps calculate the Power (P) in a circuit P = I * V P = V2 /R P = I2 * R • If you know any 2 values, you can find the third one. 5 © 2017 AVIXA Current and Voltage • Expressed in amps by the symbol “I” • The force that causes the electrons to - The flow of electrons in a circuit flow. - In a DC circuit the flow is in one - Expressed in Volts or V (or E, Electromotive Force) direction back to source - Mic level .002V - In an AC circuit the flow reverses - Line level 0.316V (consumer) or periodically. 1.23V(pro) • I = V / R - Loudspeaker level up to 100V • V = I * R 6 © 2017 AVIXA Resistance • The opposition to the flow of electrons - Expressed in ohms (O) and by the symbol R - Applies to DC (e.g. battery) - For AC is called Impedance (Z), to be discussed later • R = V / I 7 © 2017 AVIXA Activity: Ohm's Law Calculations Calculate the current in a circuit where the voltage is 2V and resistance is 8 ohms.
    [Show full text]
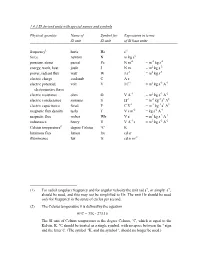
  • 1.4.3 SI Derived Units with Special Names and Symbols
    1.4.3 SI derived units with special names and symbols Physical quantity Name of Symbol for Expression in terms SI unit SI unit of SI base units frequency1 hertz Hz s-1 force newton N m kg s-2 pressure, stress pascal Pa N m-2 = m-1 kg s-2 energy, work, heat joule J N m = m2 kg s-2 power, radiant flux watt W J s-1 = m2 kg s-3 electric charge coulomb C A s electric potential, volt V J C-1 = m2 kg s-3 A-1 electromotive force electric resistance ohm Ω V A-1 = m2 kg s-3 A-2 electric conductance siemens S Ω-1 = m-2 kg-1 s3 A2 electric capacitance farad F C V-1 = m-2 kg-1 s4 A2 magnetic flux density tesla T V s m-2 = kg s-2 A-1 magnetic flux weber Wb V s = m2 kg s-2 A-1 inductance henry H V A-1 s = m2 kg s-2 A-2 Celsius temperature2 degree Celsius °C K luminous flux lumen lm cd sr illuminance lux lx cd sr m-2 (1) For radial (angular) frequency and for angular velocity the unit rad s-1, or simply s-1, should be used, and this may not be simplified to Hz. The unit Hz should be used only for frequency in the sense of cycles per second. (2) The Celsius temperature θ is defined by the equation θ/°C = T/K - 273.15 The SI unit of Celsius temperature is the degree Celsius, °C, which is equal to the Kelvin, K.
    [Show full text]