The Problem of Allocating Emergency Units: a TU-Games Approach
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Gruppo CAP Case Study SUMMARY
FULL SCALE BIOREFINERY AND TERRITORIAL STRATEGY FOR RESOURCE RECOVERY AND REUSE The Gruppo CAP Case Study SUMMARY GRUPPO CAP FROM THE SUSTAINABILITY PLAN TO THE MASTER PLAN A LIVING LAB TO TRAIN OUR TEAMS FIRST OUTCOMES THE BIOREFINERY DIGITALIZATION AND NETWORKING AS ENABLERS CONCLUSIONS GRUPPO CAP Investments of the italian water utilities – benchmark 2017 Investiments on Investments population on revenues Medium/Big Water 34 €/p.c. 22% Utilities* CAP Holding 46 €/p.c 33% GRUPPO CAP - SUSTAINABILITY PLAN 2033 https://sostenibilita.gruppocap.it/application/files/5515/5964/3927/CAP_Piano_sostenibilita_2033.pdf THE MASTER PLAN ▪ Gruppo CAP provides municipal water and wastewater services Biopolimeri PHA (ton/anno) to over 2 million inhabitants, producing in 61 waste-water treatment plants where almost 80.000 ton/year dewatered Fosforo come struvite (ton/anno) sludge is produced. Totale GRUPPO CAP ▪ In such a scenario Gruppo CAP can and wants to deliver a Peschiera B. circular economy approach. To this aim Gruppo CAP has defined Sesto S.G. a territorial Master Plan to implement eco-innovative and energy-efficient solutions to Robecco ▪ renovate and innovate existing wastewater treatment Bresso plants Pero ▪ close the circular value chain by applying low-carbon techniques to recover materials that are otherwise lost. 0 500 1000 1500 ▪ The existing municipal wastewater treatment plants can be renovated and integrated to become multi- purpose urban biorefineries that serve the citizens to treat and valorize municipal waste streams, such as -

Dgr 18 Giugno 2018
D.g.r. 18 giugno 2018 - n. XI/239 La pianificazione di Gruppo CAP Settembre 2018 016 CHI SIAMO Il Gruppo CAP è il gruppo industriale che gestisce l’intero Servizio Idrico Integrato (acquedotto, fognatura e depurazione) nei territori della Città Metropolitana di Milano e in alcuni comuni delle province di Monza-Brianza, Pavia, Varese e Como. I NUMERI D.g.r. 18 giugno 2018 – n. XI/239 - sintesi Verifica del rischio idraulico (in attuazione art. 19 bis, 38 bis e 62 N.d.A. del PAI): • Impianti di trattamento delle acque reflue urbane potenzialità > 2.000 A.E. • Impianti di captazione e trattamento di acque destinate ad uso potabile Entro le fasce: • Fasce PAI A (di deflusso della piena in cui fluisce 80% TR 200 anni) e B (di esondazione TR 200 anni) • Aree di dissesto idrogeologico Ee (con pericolosità molto elevata) o Eb (con pericolosità elevata) • Aree da mappe pericolosità del PGRA P3/H (alluvioni frequenti TR 10-20 anni) e P2/M (alluvioni poco frequenti TR 100-200 anni) Tempistiche • Contestualmente alla richiesta di rinnovo dell’autorizzazione allo scarico per depuratori o concessione di derivazione potabilizzazione • Entro 6 mesi dalla richiesta da parte delle Autorità Competenti Progettazione di riduzione del rischio idraulico di eventuali interventi di adeguamento necessari a ridurre la vulnerabilità degli impianti e i potenziali danni sull’ambiente a seguito del coinvolgimento degli impianti in un evento alluvionale entro 6 mesi dalla trasmissione della verifica di rischio idraulico Impianti di trattamento acque reflue ANAGRAFICA -

Pubblicità Bando Mobilità Esterna
Daniela Per Messi Petronio///COMUNE /COMUNE DI VILLASANTA CC 20/04/2010 11.29 CCR Oggetto pubblicità bando mobilità esterna ------------------------------------------- Daniela Petronio Ufficio Relazioni con il Pubblico Comune di Villasanta (Mi) Tel.: 039 237 54 247 ----- Inoltrato da Daniela Petronio/COMUNE DI VILLASANTA il 20/04/2010 11.29 ----- """Siverio"Siverio Barbara --- Per: "'Comune di Arluno'" <[email protected]>, "'Comune di Settore Personale --- Binasco'" <[email protected]>, "'Comune di Bresso'" Comune di Bareggio <[email protected]>, "'Comune di Brugherio'" \\\(\(((MIMIMI\\\\)")")")" <[email protected]>, "'Comune di Castano Primo'" <<<siverio<siverio...barbara .barbara@@@comu @comu <[email protected]>, "'Comune di Cavenago nene....bareggiobareggio ...mi .mimi....itititit>>>> Brianza'" <[email protected]>, 20/04/2010 09.58 "'Comune di Cerro al Lambro'" <[email protected]>, "'Comune di Cesano Boscone'" <[email protected]>, "'Comune di Corbetta'" <[email protected]>, "'Comune di Gessate'" <[email protected]>, "'Comune di Giussano'" <[email protected]>, <[email protected]>, "'Comune di Inzago'" <[email protected]>, "'Comune di Lacchiarella'" <[email protected]>, "'Comune di Lainate'" <[email protected]>, "'Comune di Lazzate'" <[email protected]>, "'Comune di Legnano'" <[email protected]>, "'Comune di Lentate -

Isu Bocconi Housing Application Requirements and Regulations
ISU BOCCONI HOUSING APPLICATION REQUIREMENTS AND REGULATIONS BOCCONI UNIVERSITY 2018-2019 A/Y FINAL REGULATIONS These Application Requirements and Regulations are to be considered final unless further dispositions concerning the evaluation of the applicants’ economic condition are issued by the relevant authorities. Student Affairs Division ISU Bocconi Fees, Funding and Housing Office Centro per il Diritto allo Studio Universitario TABLE OF CONTENTS SECTION 1: GENERAL INFORMATION 1.1 List of Bocconi Residence Halls for A/Y 2018-19 1.2 Housing rates 1.3 Who may reside in Bocconi Residence Halls 1.4 General access and cohabitation rules SECTION 2: HOUSING RENEWAL 2.1 REDUCED RATE: RENEWAL APPLICATION 2.1.1 Requirements for submitting application 2.1.2 Timescales and methods for submitting application and necessary documentation 2.1.3 Publication of outcomes and assignment 2.2 FULL RATE: RENEWAL APPLICATION 2.2.1 Requirements for submitting application 2.2.2 Timescales and methods for submitting application 2.2.3 Publication of outcomes and assignment SECTION 3: NEW HOUSING ADMISSION – FIRST ASSIGNMENTS 3.1 REDUCED RATE: NEW ADMISSION APPLICATION FOR FIRST YEAR STUDENTS AND LATER YEARS 3.1.1 Requirements for submitting application 3.1.2 Timescales and methods for submitting application and documentation 3.1.3 Publication of outcomes and assignment 3.1.4 Housing renewal criteria from A/Y 2019-20 3.2 FULL RATE: NEW ADMISSION APPLICATION FOR FIRST YEAR STUDENTS 3.2.1 Requirements for submitting application 3.2.2 Timescales and methods for submitting -

Regione Lombardia
WP C – Parma - 04.05.2018 Strategia regionale per l’inquinamento diffuso – L’esperienza di Regione Lombardia AMIIGA, Regione Lombardia – PP6 - Marina Bellotti, Donata Balzarolo Legal framework Strategy 1st Management AMIIGA Project – for the Diffuse adopted by Plan – North East Pilot Action Pollution Lombardy Milan Region TAKING COOPERATION FORWARD 2 LEGAL FRAMEWORK Three different levels: • European (EC) • Directive 2000/60/EC – Water Framework Directive (WFD) • Directive 2001/42/EC – Strategic Environmental Assessment Directive (SEA) • National (Italy) • Dlgs 152/06 delegates Regions to enact actions when diffuse contamination is recognized: • Regional (Lombardy Region) • Regional Remediation Program (RRP) including the Management Plan for Groundwater Diffuse Pollution (D.G.R. 1990/2014) TAKING COOPERATION FORWARD 3 DIRECTIVE 2000/60/EC – WATER FRAMEWORK DIRECTIVE Water management is linked to many policies: integration is the only way forward for sustainable water use Good chemical is the objective set by the WFD. Member States must use geological data to identify distinct volumes of water in underground aquifers and limit abstraction to a portion of the annual recharge. Groundwater should not be polluted at all – any pollution must be detected and stopped. Quality Standards It highlights the importance of groundwater bodies: Member States must designate separate bodies and ensure that each one achieves “good status” by 2015 (!!). TAKING COOPERATION FORWARD 4 DIRECTIVE 2001/42/EC – STRATEGIC ENVIRONMENTAL ASSESSMENT DIRECTIVE SEA - -

Comune Di Vermezzo Con Zelo
Comune di Vermezzo con Zelo Piazza Comunale, 4 20080 Vermezzo con Zelo (MI) C.F./P.IVA: 10708190961 DETERMINAZIONE DEL RESPONSABILE REGISTRO GENERALE Numero Data 69 16-03-2020 Servizio: Servizio Tecnico Responsabile del Servizio: TOSI JVAN AFFIDAMENTO IN GLOBAL SERVICE DEI SERVIZI CIMITERIALI OGGETTO: PERIODO 01/04/2020 – 31/12/2021 – AGGIUDICAZIONE - CIG 8195125F13 RICHIAMATA la determinazione n. 27 del 05/02/2020 avente ad oggetto “Affidamento in Global Service dei servizi cimiteriali periodo 01/04/2020 – 31/12/2021 – Determinazione a contrarre e impegno di spesa CIG 8195125F13”. DATO ATTO che: In data 11/02/2020, con procedura Sintel id n. 121531015 veniva avviata la manifestazione di interessi finalizzata ad acquisire almeno n. 5 autocandidature (report della procedura Sintel id n. 121531015, allegato al presente atto quale parte integrante e sostanziale - ALL. A); In data 26/02/2020, termine fissato per la scadenza della presentazione delle manifestazioni di interesse, risultavano pervenute le seguenti adesioni di n. 7 operatori economici : 1. Cooperativa ANTARES SERVIZI a r.l. 2. Depac Società Cooperativa Sociale arl 3. EUREKA s.r.l. 4. I.P.S.A. SRL 5. SOCIETA' COOPERATIVA SOCIALE IL GIARDINONE 6. GMC MULTISERVICE Documento firmato digitalmente ai sensi del D.Lgs. 82 del 2005 e ss.mm.ii. 7. Dugoni Soc. Coop. In data 02/03/2020, con precedura Sintel id n. 122382709 venivano invitati a presentare offerta tutti gli operatori economici che avevano manifestato interesse alla procedura. In data 12/03/2020, termine fissato per la presentazione delle offerte, risultavano pervenute le offerte presentate dai seguenti operatori : 1. -

Distretto Ambito Distrettuale Comuni Abitanti Ovest Milanese Legnano E
Ambito Distretto Comuni abitanti distrettuale Busto Garolfo, Canegrate, Cerro Maggiore, Dairago, Legnano, Nerviano, Legnano e Parabiago, Rescaldina, S. Giorgio su Legnano, S. Vittore Olona, Villa 22 254.678 Castano Primo Cortese ; Arconate, Bernate Ticino, Buscate, Castano Primo, Cuggiono, Inveruno, Magnano, Nosate, Robecchetto con Induno, Turbigo, Vanzaghello Ovest Milanese Arluno, Bareggio, Boffalora sopra Ticino, Casorezzo, Corbetta, Magenta, Magenta e Marcallo con Casone, Mesero, Ossona, Robecco sul Naviglio, S. Stefano 28 211.508 Abbiategrasso Ticino, Sedriano, Vittuone; Abbiategrasso, Albairate, Besate, Bubbiano, Calvignasco, Cisliano, Cassinetta di Lugagnano, Gaggiano, Gudo Visconti, Morimomdo, Motta Visconti, Ozzero, Rosate, Vermezzo, Zelo Surrigone Garbagnate Baranzate, Bollate, Cesate, Garbagnate Mil.se, Novate Mil.se, Paderno 17 362.175 Milanese e Rho Dugnano, Senago, Solaro ; Arese, Cornaredo, Lainate, Pero, Pogliano Rhodense Mil.se, Pregnana Mil.se, Rho, Settimo Mil.se, Vanzago Assago, Buccinasco, Cesano Boscone, Corsico, Cusago, Trezzano sul Corsico 6 118.073 Naviglio Sesto San Giovanni, Cologno Monzese, Cinisello Balsamo, Bresso, Nord Milano Nord Milano 6 260.042 Cormano e Cusano Milanino Milano città Milano Milano 1 1.368.545 Bellinzago, Bussero, Cambiago, Carugate, Cassina de Pecchi, Cernusco sul Naviglio, Gessate, Gorgonzola, Pessano con Bornago, Basiano, Adda Grezzago, Masate, Pozzo d’Adda, Trezzano Rosa, Trezzo sull’Adda, 28 338.123 Martesana Vaprio d’Adda, Cassano D’Adda, Inzago, Liscate, Melzo, Pozzuolo Martesana, -
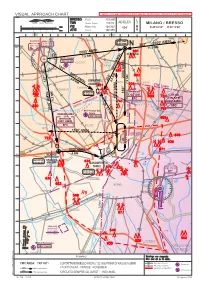
Bresso Visual Approach Chart
Lago di Annone Lago di Garlate COMO Lago di Pusiano OLGINATE COMO ATZ (G) Lago di OLGIATE 1000’ SFC COMASCO Lago di Alserio SFC Montorfano 1000’ AGL or 2000’ AMSL Whichever is whicher FINO MORNASCO OGGIONO ALZATE ATZ (G) APPIANO 700’ SFC CANTU’ GENTILE SFC BRIVIO VISUAL APPROACH CHART NOT TO BE USED FOR REAL NAVIGATIONAL PURPOSES BESANA Radio 122.005 L aero club milano Linate Tower 118.10 AD ELEV I MILANO IN/ BRIANZABRESSO MERATE 1 2 3 Milano Info 124.925 484’ M N 45°32'29" E 09°12'08" 1 2 3 4 5 Linate 136.375 B 9° 00’ 9° 10’ CARATE BRIANZA Mocchirolo TMA (A) SARONNO VOR N 45°39'48'’ VOR-DME-L N 45 38.80 AMSL CALUSCO 0 E 09°12'06'’ 2000’ MILANO 45° SRN 113.7 E 09 01.40 N 262° 3 Fiume FL 195 40’ 33033 11.3 NM 6 AMSL 2500' 30 * 2000’ SEREGNO or 1500' SFC 82° 7.8 NM whichever* is higher 9 MI 17-3 Cogliate 27 RDO 130.000 COGLIATE CESANO 12 24 120° MADERNO ADDASUISIO MACHERIO SARONNO15 2000’AMSL 21 18 ARCORE 2000’AMSL 6.0 NM 2000’AMSL 206° 167° CIMINIERE sector 4.8 NM DESIO LISSONE VIMERCATE 7.5 NM CHIMNEY CTR Linate TREZZO VFR Limbiate GARBAGNATE ATZ SULL’ADDA BRESSO N 45°35'30'’ C 180° E 09°09'00'’ 1200' AGL CTR (D) AREA 1500’AMSL SFC LINATE AMSL 8.2 NM 8.2 MONZA 2000' AMSL - WORKINGi s 140° Vi l l o r TZ e SFC BRESSO e 2.2 NM A r s Lainate 2000’ o MI 15-4 Campo Volo 1500’ l l i WORKING AREAV i Groane (G) RDO 130.000 BRESSO BRESSO AGRATE 3000' AMSL CINISELLO SFC BOLLATE Villoresi RHO 18 1500’ AMSL BRESSO NDB 514 Cologno NO ID 36 O 2000’AMSL GORGONZOLA 50° 45° INCROCIO 4 NM T 30’ AUTOSTRADE 1.3 NM 1500’ N 45°30'36'’ CROSSING E 09°03'36'’ -

Calendario Seconda Categoria
* COMITATO * F. I. G. C. - LEGA NAZIONALE DILETTANTI * LOMBARDIA * ************************************************************************ * * * SECONDA CATEGORIA MILANO GIRONE: P * * * ************************************************************************ .--------------------------------------------------------------. .--------------------------------------------------------------. .--------------------------------------------------------------. I ANDATA: 4/09/16 ! ! RITORNO: 15/01/17 I I ANDATA: 9/10/16 ! ! RITORNO: 19/02/17 I I ANDATA: 13/11/16 ! ! RITORNO: 26/03/17 I I ORE...: 15:30 ! 1 G I O R N A T A ! ORE....: 14:30 I I ORE...: 15:30 ! 6 G I O R N A T A ! ORE....: 14:30 I I ORE...: 14:30 ! 11 G I O R N A T A ! ORE....: 15:30 I I--------------------------------------------------------------I I--------------------------------------------------------------I I--------------------------------------------------------------I I ARDOR BOLLATE - PRO NOVATE I I BRUZZANO - OSAL NOVATE I I AFFORESE - BRUZZANO I I BRUZZANO - MASCAGNI I I CITTA DI SESTO - NIGUARDA CALCIO I I ARDOR BOLLATE - FOOTBALL CLUB BRESSO I I FOOTBALL CLUB BRESSO - SPERANZA PRIMULE I I MASCAGNI - PALAZZOLO MILANESE I I CIRCOLO GIOVANILE BRESSO - SOLESE A.S.D. I I NIGUARDA CALCIO - CIRCOLO GIOVANILE BRESSO I I PRO NOVATE - FOOTBALL CLUB BRESSO I I NIGUARDA CALCIO - REAL CINISELLO I I OSAL NOVATE - RONDINELLA A.S.D. I I RONDINELLA A.S.D. - AFFORESE I I PALAZZOLO MILANESE - OSAL NOVATE I I PALAZZOLO MILANESE - AFFORESE I I SAN GIORGIO - CIRCOLO GIOVANILE BRESSO I I RONDINELLA -

2016 Italian Food Retail and Distribution Sector Report Retail Foods Italy
THIS REPORT CONTAINS ASSESSMENTS OF COMMODITY AND TRADE ISSUES MADE BY USDA STAFF AND NOT NECESSARILY STATEMENTS OF OFFICIAL U.S. GOVERNMENT POLICY Required Report - public distribution Date: 12/13/2016 GAIN Report Number: IT1655 Italy Retail Foods 2016 Italian Food Retail and Distribution Sector Report Approved By: Fred Giles Prepared By: Dana Biasetti Report Highlights: In 2015, after years of deep recession, Italy showed signs of a long-awaited economic recovery. Affected by diminished disposable incomes and high unemployment, Italian consumers remain very price conscious and tend to seek discounts. With tighter wallets, their changing shopping strategies indicate that now more than ever, they are avidly pursuing true bargains. Major retail brands have embraced the “everyday low price” strategies, increasing their private label ranges. This report provides an overview of the grocery retail sector and how best to place U.S. products in the Italian market. 1 Post: Rome Executive Summary: Section I. Market Summary Italy has a diversified industrial economy, divided into a developed industrial north and a less- developed agricultural south, with high unemployment. The Italian economy is driven in large part by the manufacture of high-quality consumer goods produced by small and medium-sized enterprises, many of them family owned. Italy is the third-largest economy in the euro-zone, but exceptionally high public debt burdens and structural impediments to growth have rendered it vulnerable to scrutiny by financial markets. Italy’s GDP is estimated at $2.175 trillion, and it has a per capita GDP of $35,800. Italy has few natural resources, with much land unsuited for farming. -

UNEP EXCEL 2.Xlsx
agenzia trotta srl DISTRETTO DELLA CORTE D'APPELLO DI MILANO UNEP MILANO ‐ ELENCO COMUNI CON NOTIFICA A MANI AFFORI ARESE (Valera) ARLUNO (Rogorotto) ASSAGO BARANZATE di BOLLATE BAREGGIO (Cascine) BASIANO BASIGLIO BELLINZAGO LOMBARDO BERNATE TICINO (Casate) BOFFALORA SOPRA TICINO (Ponte Nuovo) BOLLATE (Cassina Nuova; Castellazzo, Cascina del Sole, Ospiate BRESSO BRUZZANO (Niguarda) BUCCINASCO (Gudo Gambaredo, Romanobanco) BUSSERO CAMBIAGO (Torrazza) CASOREZZO CASSANO D'ADDA CASSINA DE' PECCHI (Sant'Agata, Camporicco) CERNUSCO SUL NAVIGLIO (Ronco) CESANO BOSCONE CESATE CORBETTA (Castellazzo, Soriano, Cerello, Battuello) CORMANO‐BRUSUGLIO (Ospitaletto di Cormano) CORNAREDO (San Pietro all'Olmo) CORSICO CUGGIONO (Castelletto) CUSAGO (Monzoro) FIGINO GARBAGNATE MILANESE (Bariana, Santa Maria Rossa) GESSATE (Villa Formaci) GORGONZOLA GREZZAGO GUDO LOMBARDO INVERUNO (Furato) Copyright © 2016, Agenzia Trotta Srl. 1 di 2 INZAGO LAINATE (Barbaiana, Grancia, Pegliera) LIMBIATE (Mombello) LISCATE MAGENTA (Pontenuovo) MARCALLO CON CASONE MESATE MELZO MESERO MILANO NERVIANO (San Lorenzo) NOVATE MILANESE OPERA OSSONA PANTIGLIATE PERO (Cerchiate, Cerchiarello) PESCHIERA BORROMEO (Zeloforamagno, Bettola, Mezzate, Mirazzano, San Bovio) PESSANO CON BORNAGO PIEVE EMANUELE (Fizzonasco, Tolcinasco; Pizzabraso) PIOLTELLO (Limito. Seggiano) POGLIANO MILANESE POZZO D'ADDA (Bettola) POZZUOLO MARTESANA (Bisentrate, Trecella) PREGNANA MILANESE RHO (Passirama, Lucernate, Biringhello, Castellazzo, Pantanedo, Mazzo, Terrazzano) RODANO (Cassignanica, Mille Pini) ROZZANO -

Right to Education Call for Applications Istituto
RIGHT TO EDUCATION CALL FOR APPLICATIONS for the assignment of financial aid and study grants ISTITUTO EUROPEO DI DESIGN MILAN ROME TURIN CAGLIARI FLORENCE 1 Call For Application 18_19 Contents 1. ELIGIBLE APPLICANTS 2. SUM SET ASIDE FOR STUDY GRANTS 3. REQUIREMENTS 3.1 Merit requirements 3.2 Economic requirements 4. VALUE OF STUDY GRANTS 5. INTEGRATION TO THE STUDY GRANTS 6. PROCEDURES FOR PREPARING THE RANKING LISTS 7. DEADLINES 8. HOW TO APPLY 9. TRANSFER 9.1 Presentation of the application in the event of transfer to another university 9.2 Presentation of the application in the event of transfer from another university 10. NON-ADMISSION TO THE CALL FOR APPLICATIONS 11. PUBLICATION OF THE RANKING LISTS AND APPEALS 12. ASSIGNMENT OF STUDY GRANTS AND PAYMENT TERMS 13. INADMISSIBILITY, FORFEITURE, REVOCATION OF THE RIGHT 14. CHECKS ON THE TRUTHFUL NATURE OF ECONOMIC DECLARATION PROVIDED 15. INFORMATION ON THE USE OF PERSONAL DATA AND THE RIGHTS OF THE DECLARANT (Art. 13 of the Europian regulation on data protection no.2016/679 GDPR) 16. REMINDER DEADLINES APPENDIX A, B, C, D and E 2 Call For Application 18_19 1. ELIGIBLE APPLICANTS The call for applications is open to everybody: - Italian citizens, - Citizens of European Union Member States, - Citizens of States not belonging to the European Union (Italian Presidential Decree no. 394 dated 31st August 1999, implementing Italian Legislative Decree no. 286 dated 25th July 1998). Applicants must meet all the following requirements: - be a IED student admitted or enrolled in an Academic Diploma First Level course at Istituto Europeo di Design, in the seats of Milan, Rome, Turin, Cagliari or Florence, for the Academic Year 2018/2019; - Have the economic and merit requirements listed in point 3.