DOCSLIB.ORG

A Method for Optical Tracking of On-Orbit Servicing Operations in Geostationary Orbit Using Speckle Interferometry

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Method for Optical Tracking of On-Orbit Servicing Operations in Geostationary Orbit Using Speckle Interferometry A Method for Optical Tracking of On-Orbit Servicing Operations in Geostationary Orbit Using Speckle Interferometry by Robert L. Scott, M.S., P.Eng. A thesis submitted to the Faculty of Graduate and Postdoctoral Affairs in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Aerospace Engineering Carleton University Ottawa, Ontario ©Her Majesty the Queen in Right of Canada, as represented by the Minister of National Defence, 2015 Abstract On Orbit Servicing (OOS) is a class of space missions that could potentially extend the life of orbiting satellites by fuel replenishment, repair, orbital maintenance or satellite repurposing, and possibly reduce the rate of space debris generation. OOS performed in geostationary orbit poses a unique challenge for the optical space surveillance community. OOS satellites performing close proximity operations with separations less than 1 km in geosynchronous orbit subtend an angle comparable to the angular size of atmospheric seeing (turbulence) cells as viewed by a ground-based observer. This degrades the ability of a ground-based observer from resolving a geostationary satellite pair in order to perform astrometric measurements on the objects’ relative positions. In this research, a speckle-interferometric observational approach designed to detect and estimate the relative orbits of servicing satellites about their client is described. It was found that the use of the cross-spectrum of speckle imagery and extraction of its imaginary component provides unambiguous measurables useful for relative orbit estimation for closely-spaced satellites. This approach is enabled by the availability sensitive Electron Multiplying CCD (EMCCD) cameras which permit the detection of very faint speckles from an astronomical source. This thesis describes an observational model, the speckle-imaging acquisition process, an image-processing algorithm and experimental test results pertaining to the speckle measurement of very closely-spaced satellites. Testing of the cross-spectrum technique was conducted by observing rare optical alignments (optical conjunctions) of co-located geostationary satellites using medium and small aperture telescopes configured to perform speckle interferometry. Satellite pairs of magnitudes of Mprimary = 10.3, Δm = 0.3 and Mprimary = 9.0, Δm = 1.5 were observed with the 1.6-m Mont-Mégantic telescope. Minimum detected separations between the two satellites of 1.5 arcseconds were achieved. A subsequent small aperture telescope test successfully detected a satellite pair of Mprimary = 9.67, Δm = 1.63. It was found that in- track and cross-track relative orbit positions precise to 100 meters with respect to reference ephemeris provided by a satellite operator was achieved and evidence is shown that 50-meter precision is possible with longer observational periods. ii It was also found that due to the satellites’ relatively high relative motion rates that strong fringe rotation affected the separation measurements. This issue is less likely to affect real OOS satellite cases as the relative separation distances between them are much less than co-located satellites making their relative angular velocities much smaller in comparison. A technique to handle cases when the fringes are rotating at an excessive rate was developed and was found to be a more reliable approach to detecting the separation distance of the secondary satellite. In order to use speckle interferometry to measure the relative orbits of satellites in close proximity to one another a visibility requirement must be respected. This is due to atmospheric turbulence where both satellites must fall within the isoplanatic patch (< 5 arcsecond conical radius) before speckle patterns can be reliably acquired. This angle sets an upper limit on the separation of the satellite pair of ~1 km in geosynchronous orbit. Further to this, the seeing conditions must be steady during observation in order to ensure that the fringe measurements are reliably correlated during image processing. Due to the dynamic coupling between the radial and in-track motion of a servicer about its client, the radial component requires ~3 hours of observations to reliably estimate it. This is due to a partial observability limitation where the near-alignment of the camera field of view and the radial direction of the client coordinate frame are nearly co-linear. While partial observability of the radial component of the servicer’s motion is detectable the relative orbit is overall observable due to the dynamic coupling between the in-track and radial directions. iii Acknowledgements It is a pleasure to acknowledge the tremendous support of the women and men of the Canadian Armed Forces who watch the skies to maintain Canada’s position as a leader in the emerging field of Space Situational Awareness. I am very grateful to Defense Research and Development Canada who provided funding support for this work while I worked on the development of the NEOSSat microsatellite project and the Ground Based Optical space surveillance system. Appreciation is extended to: Gary Geling, Malcom Vant, Maria Rey, Caroline Wilcox, Dr. Brad Wallace, Stefan Thorsteinson, Major Donald Bedard, Lt Colonel Aaron Spaans, Lt Colonel Pascal Tremblay, Lt Colonel Catherine Marchetti, Dr Scott McLelland, Paul Pulsifer, Brian Eatock, Chris McMillan, John Weaver who have all played a role helping me either build sensors or collect observational data when I needed it. I also wish to acknowledge the talented engineering teams at the Department of National Defence who built Canada's first space based space surveillance satellites SAPPHIRE and NEOSSat, without whom I would not have learned the technical boundaries about the field of space surveillance. It has been my privilege to play a part in the Canadian Armed Forces’ role in Space Situational Awareness. From Carleton University, I wish to acknowledge my thesis advisor Dr. Alex Ellery who also gave me the tremendous flexibility needed to accommodate both my graduate studies while working as a mission scientist on NEOSSat. Bruce Burlton provided tremendous insights into flight operations at Telesat Canada. Both of these professors’ experiences led to the combined topic of space surveillance of robotic On-Orbit Servicing in GEO. I would also like to acknowledge the talented staff of the Mont-Mégantic observatory in Mont-Mégantic, Quebec and the University of Montreal for their generous granting of observational time on the 1.6m telescope. This work would not have been possible without access to one of the highest performance EMCCD cameras available and appreciation to Nuvu Camera Inc.; Oliver Daigle, Felecien Legrand and Phillipe Richelet is extended. Tim Douglas at Telesat Canada provided tremendous support by supplying satellite orbital ephemerides, without which the experimental portions of this research would not have been possible. iv My family has been so supportive and I also wish to extend a thank you to my mother Bonnie, father Lauchie and my partner Rebecca for their continued patience and encouragement. You have all been so generous and your kindness will not be forgotten. My grandfather once said that “education doesn’t cost anything to carry around”. This wise advice has always steered my endeavors in that knowledge is the best investment one can make in oneself and in others. Per aspera ad astra….. Robert Lauchlan Scott v Table of Contents Abstract ......................................................................................................................... ii Acknowledgements ...................................................................................................... iv Table of Contents ........................................................................................................ vi List of Tables ............................................................................................................... xi List of Illustrations ..................................................................................................... xii List of Appendices ................................................................................................... xviii Chapter 1: Introduction ........................................................................................... 1 1.1 On Orbit Servicing as a space surveillance problem ...................................... 1 1.2 A short overview of On-Orbit-Servicing missions ......................................... 2 1.3 Geostationary orbit.......................................................................................... 5 1.4 Space surveillance and the problem of OOS in GEO ..................................... 7 1.5 Motivation for this research: Space surveillance of closely-spaced objects . 10 1.5.1 The OOS problem ................................................................................. 14 1.6 Thesis problem statement ............................................................................. 15 1.6.1 Initial exploration using light curve inversion ...................................... 17 1.6.2 Speckle interferometry .......................................................................... 22 1.6.3 EMCCDS .............................................................................................. 24 1.6.4 Other considered technologies: Adaptive optics ................................... 25 1.6.5 Other considered technologies: Space surveillance radars ................... 27 1.6.6 Other considered technologies:
Load more

Recommended publications
  • The Modern Broadcaster's Journey from Satellite to Ip
    A CONCISE GUIDE TO… THE MODERN BROADCASTER’S JOURNEY FROM SATELLITE TO IP DELIVERY The commercial communication satellite will celebrate its 60th birthday next year but the concept is far from entering retirement. Nonetheless, as it moves into its seventh decade, the use of the satellite is rapidly evolving. As of 2020, approximately 1,400 communications satellites are orbiting the earth, delivering tens of thousands of TV channels and, increasingly, internet connectivity. Satellite communication is also a vital asset for the TV production industry, allowing live reportage to and from anywhere in the world – almost instantly. 1 Its place in the TV ecosystem is changing, much higher value. It was also well before the however, as it plays a reduced role in the on-demand content revolution. This trend delivery of video – a shift that several has led to the last major shift: the emergence underlying trends have accelerated. The first of multiplatform, over-the-top streaming is a massive proliferation of video content. over the last 15 years, which has eroded the dominance of the linear broadcaster. The Although satellite use in TV production rise of the streaming giants and specialist has been integral to high-profile live news platforms has forced broadcasters to increase and sports coverage, its role is waning. The their overall distribution capacity using last couple of decades has seen a massive Internet Protocol (IP)-centric methods. increase in live content from a broader range of leagues, niche sports, performance The trends impacting satellite’s role in events and 24-hour news networks. This the television landscape are forcing many expansion of content leads to the second broadcasters to look to their future and factor.
    [Show full text]
  • Low-Cost Wireless Internet System for Rural India Using Geosynchronous Satellite in an Inclined Orbit
    Low-cost Wireless Internet System for Rural India using Geosynchronous Satellite in an Inclined Orbit Karan Desai Thesis submitted to the faculty of the Virginia Polytechnic Institute and State University in partial fulfillment of the requirements for the degree of Master of Science In Electrical Engineering Timothy Pratt, Chair Jeffrey H. Reed J. Michael Ruohoniemi April 28, 2011 Blacksburg, Virginia Keywords: Internet, Low-cost, Rural Communication, Wireless, Geostationary Satellite, Inclined Orbit Copyright 2011, Karan Desai Low-cost Wireless Internet System for Rural India using Geosynchronous Satellite in an Inclined Orbit Karan Desai ABSTRACT Providing affordable Internet access to rural populations in large developing countries to aid economic and social progress, using various non-conventional techniques has been a topic of active research recently. The main obstacle in providing fiber-optic based terrestrial Internet links to remote villages is the cost involved in laying the cable network and disproportionately low rate of return on investment due to low density of paid users. The conventional alternative to this is providing Internet access using geostationary satellite links, which can prove commercially infeasible in predominantly cost-driven rural markets in developing economies like India or China due to high access cost per user. A low-cost derivative of the conventional satellite-based Internet access system can be developed by utilizing an aging geostationary satellite nearing the end of its active life, allowing it to enter an inclined geosynchronous orbit by limiting station keeping to only east-west maneuvers to save fuel. Eliminating the need for individual satellite receiver modules by using one centrally located earth station per village and providing last mile connectivity using Wi-Fi can further reduce the access cost per user.
    [Show full text]
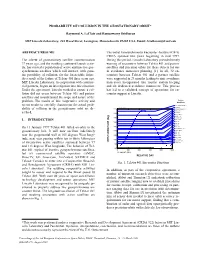
  • Probability of Collision in the Geostationary Orbit*
    PROBABILITY OF COLLISION IN THE GEOSTATIONARY ORBIT* Raymond A. LeClair and Ramaswamy Sridharan MIT Lincoln Laboratory, 244 Wood Street, Lexington, Massachusetts 02420 USA, Email: [email protected] ABSTRACT/RESUME The initial Geosynchronous Encounter Analysis (GEA) CRDA spanned two years beginning in mid 1997. The advent of geostationary satellite communication During this period, Lincoln Laboratory provided timely 37 years ago, and the resulting continued launch activ- warning of encounters between Telstar 401 and partner ity, has created a population of active and inactive geo- satellites and precision orbits for these objects for use synchronous satellites which will interact, with genu- in avoidance maneuver planning [1]. In all, 32 en- ine possibility of collision, for the foreseeable future. counters between Telstar 401 and a partner satellite As a result of the failure of Telstar 401 three years ago, were supported in 24 months leading to nine avoidance MIT Lincoln Laboratory, in cooperation with commer- maneuvers incorporated into routine station keeping cial partners, began an investigation into this situation. and six dedicated avoidance maneuvers. This process Under the agreement, Lincoln worked to ensure a col- has led to a validated concept of operations for en- lision did not occur between Telstar 401 and partner counter support at Lincoln. satellites and to understand the scope and nature of the Active problem. The results of this cooperative activity and Satellites recent results to carefully characterize the actual prob- SOLIDARIDAD 02 ANIK E1 04-Oct-1999 ability of collision in the geostationary orbit are de- 114 SOLIDARIDAD 1 GOES 07 scribed. ANIK E2 112 MSAT M01 ) ANIK C1 110 GSTAR 04 deg USA 0114 1.
    [Show full text]
  • Optical Satellite Communication Toward the Future of Ultra High
    No.466 OCT 2017 Optical Satellite Communication toward the Future of Ultra High-speed Wireless Communications No.466 OCT 2017 National Institute of Information and Communications Technology CONTENTS FEATURE Optical Satellite Communication toward the Future of Ultra High-speed Wireless Communications 1 INTERVIEW New Possibilities Demonstrated by Micro-satellites Morio TOYOSHIMA 4 A Deep-space Optical Communication and Ranging Application Single photon detector and receiver for observation of space debris Hiroo KUNIMORI 6 Environmental-data Collection System for Satellite-to-Ground Optical Communications Verification of the site diversity effect Kenji SUZUKI 8 Optical Observation System for Satellites Using Optical Telescopes Supporting safe satellite operation and satellite communication experiment Tetsuharu FUSE 10 Development of "HICALI" Ultra-high-speed optical satellite communication between a geosynchronous satellite and the ground Toshihiro KUBO-OKA TOPICS 12 NICT Intellectual Property -Series 6- Live Electrooptic Imaging (LEI) Camera —Real-time visual comprehension of invisible electromagnetic waves— 13 Awards 13 Development of the “STARDUST” Cyber-attack Enticement Platform Cover photo Optical telescope with 1 m primary mirror. It receives data by collecting light from sat- ellites. This was the main telescope used in experiments with the Small Optical TrAn- sponder (SOTA). This optical telescope has three focal planes, a Cassegrain, a Nasmyth, and a coudé. The photo in the upper left of this page shows SOTA mounted in a 50 kg-class micro- satellite. In a world-leading effort, this was developed to conduct basic research on technology for 1.5-micron band optical communication between low-earth-orbit sat- ellite and the ground and to test satellite-mounted equipment in a space environment.
    [Show full text]
  • Eie312 Communications Principles
    EIE312 COMMUNICATIONS PRINCIPLES Outline: Principles of communications: 1. An elementary account of the types of transmission (Analogue signal transmission and digital signal transmission). Block diagram of a communication system. 2. Brief Historical development on communications: a. Telegraph b. Telephony c. Radio d. Satellite e. Data f. Optical and mobile communications g. Facsimile 3. The frequency Spectrum 4. Signals and vectors, orthogonal functions. 5. Fourier series, Fourier integral, signal spectrum, convolution, power and energy correlation. 6. Modulation, reasons for modulation, types of modulation. 7. Amplitude modulation systems: a. Comparison of amplitude modulation systems. b. Methods of generating and detecting AM, DBS and SSB signals. c. Vestigial sideband d. Frequency mixing and multiplexing, frequency division multiplexing e. Applications of AM systems. 8. Frequency modulation systems: 1 a. Instantaneous frequency, frequency deviation, modulation index, Bessel coefficients, significant sideband criteria b. Bandwidth of a sinusoidally modulated FM signal, power of an FM signal, direct and indirect FM generation, c. Various methods of FM demodulation, discriminator, phase-lock loop, limiter, pre- emphasis and de-emphasis, Stereophonic FM broadcasting 9. Noise waveforms and characteristics. Thermal noise, shot noise, noise figure and noise temperature. Cascade network, experimental determination of noise figure. Effects of noise on AM and FM systems. 10. Block diagram of a superheterodyne AM radio receiver, AM broadcast mixer, local oscillator design, intermodulation interference, adjacent channel interference, ganging, tracking error, intermediate frequency, automatic gain control (AGC), delay AGC, diode detector, volume control. 11. FM broadcast band and specification, Image frequency, block diagram of a FM radio receiver, limiter and ratio detectors, automatic frequency control, squelch circuit, FM mono and FM stereo receivers.
    [Show full text]
  • Overview of Satellite Communications
    Overview of Satellite Communications Dick McClure Agenda Background History Introduction to Satcom Technology Ground System Antennas Satellite technology Geosynchronous orbit Antenna coverage patterns 2 COMMUNICATION SATELLITES Uses Example satellite systems 3 Why Satellite Communications? Satellite coverage spans great distances A satellite can directly connect points separated by 1000’s of miles A satellite can broadcast to 1000’s of homes/businesses/military installations simultaneously A satellite can be reached from ground facilities that move Satellites can connect to locations with no infrastructure Satellites adapt easily to changing requirements Some Common SATCOM Systems The INTELSAT system provides globe-spanning TV coverage The Thuraya satellite-based phone system covers all of Saudi Arabia and Egypt DoD Military Communications Satellite System Links field sites with Pentagon and US command centers DirecTV, Echostar Direct-to-home TV XM Radio, Sirius Satellite radio-to-car/home Hughes VSAT (Very Small Aperture Terminal) systems Links GM car dealers, Walmart, Costco, J C Penney, etc. to their accounting centers Common Satellite Orbits LEO (Low Earth Orbit) Close to Earth Photo satellites – 250 miles Iridium – 490 miles Polar Orbit Provides coverage to polar regions (used by Russian satellites) GEO (Geosynchronous Earth Orbit) Angular velocity of the satellite = angular velocity of earth satellite appears to be fixed in space Most widely used since ground antennas need not move Circular orbit Altitude: 22,236 miles Can’t “see” the poles 6 HISTORICAL BACKGROUND People Early satellites Evolution 7 Historical Background: People Arthur C. Clarke Highly successful science fiction author First to define geosynchronous communications satellite concept Published paper in Wireless World , October 1945 Suggested terrestrial point-to-point relays would be made obsolete by satellites Unsure about how satellites would be powered John R.
    [Show full text]
  • High Latitude Communications Satellite By
    I I High Latitude Communications Satellite By I Brij N. AgrawaIt Naval Postgraduate School I Monterey. California This paper presents preliminary design of a high latitude communications satellite. The satellite provides a continuous UHF I communications for areas located north of the region covered by geosynchronous communications satellites. The satellite orbit is elliptic with 63.40 inclination with perigee at 1204 km altitude in I the southern hemisphere and apogee at 14930 km altitude. The orbit period is 4.8 hours. The system consists of three satellites equally spaced in mean anomaly. It is launched by Delta II launch I vehicle in three satellite staked configuration. The spacecraft uses three-axis-stabilization consisting of three reaction wheel system. Solar array surface is always normal to sun rays by spacecraft I rotation about yaw axis and solar array drive rotation. The propulsion subsystem is a catalytic monopropellant hydrazine subsystem. consisting of four 38-Newton and twelve 2-Newton I thrusters. Electric power is provided by GaAs solar cell and nickel hydrogen batteries. I INTRODUCTION Geosynchronous spacecraft have been widely used for communications satellites. Three equally spaced geosynchronous spacecraft can provide global I communication network. However, geosynchronous spacecraft can not provide communication for high latitude areas. A spacecraft design project was undertaken at the Naval Postgraduate School in Fall 1989 to perform I preliminary design of a high latitude communications satellites (HILACS). The paper presents the results of this study including some recent work. I SATELLITE MISSION The mission of the satellite system is to provide continuous communications for areas above 60 0 N latitude.
    [Show full text]
  • 5G New Radio Evolution Meets Satellite Communications: Opportunities, Challenges, and Solutions
    1 5G New Radio Evolution Meets Satellite Communications: Opportunities, Challenges, and Solutions Xingqin Lin, Björn Hofström, Eric Wang, Gino Masini, Helka-Liina Maattanen, Henrik Rydén, Jonas Sedin, Magnus Stattin, Olof Liberg, Sebastian Euler, Siva Muruganathan, Stefan Eriksson G., and Talha Khan Ericsson Contact: [email protected] the development cycle and the costs of satellite manufacturing Abstract— The 3rd generation partnership project (3GPP) and launching processes have been dramatically reduced [5]. completed the first global 5th generation (5G) new radio (NR) A major driver of the success of terrestrial mobile networks standard in its Release 15, paving the way for making 5G a over the past few decades has been the international commercial reality. So, what is next in NR evolution to further standardization effort yielding the benefits of significant expand the 5G ecosystem? Enabling 5G NR to support satellite economies of scale. The 3rd generation partnership project communications is one direction under exploration in 3GPP. There has been a resurgence of interest in providing connectivity (3GPP) has been the dominating standardization development from space, stimulated by technology advancement and demand body of several generations of mobile technology. The for ubiquitous connectivity services. The on-going evolution of 5G international standardization effort helps ensure compatibility standards provides a unique opportunity to revisit satellite among vendors and reduce network operation and device costs. communications. In this article, we provide an overview of use In contrast, the interoperability between different satellite cases and a primer on satellite communications. We identify key solution vendors has been difficult and the availability of technical challenges faced by 5G NR evolution for satellite devices is limited, leading to an overall fragmented satellite communications and give some preliminary ideas for how to communications market up to date [6].
    [Show full text]
  • Geosynchronous Satellite GF-4 Observations of Chlorophyll-A Distribution Details in the Bohai Sea, China
    sensors Article Geosynchronous Satellite GF-4 Observations of Chlorophyll-a Distribution Details in the Bohai Sea, China Lina Cai 1, Juan Bu 1, Danling Tang 2,*, Minrui Zhou 1, Ru Yao 1 and Shuyi Huang 1 1 Marine Science and Technology College, Zhejiang Ocean University, Zhoushan 316004, China; [email protected] (L.C.); [email protected] (J.B.); [email protected] (M.Z.); [email protected] (R.Y.); [email protected] (S.H.) 2 Southern Marine Science and Engineering Guangdong Laboratory Guangdong Key Laboratory of Ocean Remote Sensing (LORS), South China Sea Institute of Oceanology, Chinese Academy of Sciences, Guangzhou 510301, China * Correspondence: [email protected] Received: 5 August 2020; Accepted: 21 September 2020; Published: 24 September 2020 Abstract: We analyzed the distribution of chlorophyll-a (Chla) in the Bohai Sea area based on data from the geosynchronous orbit optical satellite Gaofen-4 (GF-4), which was launched in 2015, carrying a panchromatic multispectral sensor (PMS). This is the first time the geosynchronous orbit optical satellite GF-4 remote-sensing data has been used in China to detect the Chla change details in the Bohai Sea. A new GF-4 retrieved model was established based on the relationship between in situ Chla value and the reflectance combination of 2 and 4 bands, with the R2 of 0.9685 and the total average relative error of 37.42%. Twenty PMS images obtained from 2017 to 2019 were applied to analyze Chla in Bohai sea. The results show that: (1) the new built Chla inversion model PMS-1 for the GF-4 PMS sensor can extract Chla distribution details in the Bohai Sea well.
    [Show full text]
  • Evolution and Future of Broadband Satellite Services Brennan Price ITU Satellite Symposium November 29, 2018 Corporate Overview 2018 About Echostar
    Evolution and Future of Broadband Satellite Services Brennan Price ITU Satellite Symposium November 29, 2018 Corporate Overview 2018 About EchoStar We are a global powerhouse • Multibillion-dollar public company (NASDAQ:SATS) • Operates and manages 24 satellites—the world’s 4th largest commercial geosynchronous satellite fleet • World’s #1 consumer high-speed satellite internet service, HughesNet®, with over 1.3 million subscribers in the Americas • Leading global provider of satellite broadband technology and services—approximately 50% market share with over 7 million systems shipped to customers in over 100 countries on five continents • First commercial satellite network with Walmart, named one of the top 20 strategic business decisions of the 20th century by Fortune magazine © 2018 EchoStar November 29, 2018 3 Company Structure © 2018 EchoStar November 29, 2018 4 Worldwide Locations © 2018 EchoStar November 29, 2018 5 EchoStar Satellite Services © 2018 EchoStar November 29, 2018 6 Satellite Fleet • 24 owned, leased, and managed satellites • World’s fourth-largest commercial geosynchronous satellite fleet © 2018 EchoStar November 29, 2018 7 Satellite Services • Broadcast Satellite Services (BSS) ‒ Capacity for Direct-to-Home (DTH) service providers ‒ DISH Network and Dish Mexico • Fixed Satellite Services (FSS) Mexico ‒ Full and part-time Ku-band transponder capacity ‒ Enterprise, broadcast, and government services applications • Mobile Satellite Services (MSS) ‒ Mobile, public safety, and transportation applications © 2018 EchoStar
    [Show full text]
  • Regulation of Global Broadband Satellite Communications April 2012
    REGULATORY & MARKET ENVIRONMENT International Telecommunication Union Telecommunication Development Bureau Place des Nations CH-1211 Geneva 20 REGULATION OF Switzerland www.itu.int GLOBAL BROADBAND SATELLITE COMMUNICATIONS Broadband Series APRIL 2012 Printed in Switzerland Telecommunication Development Sector Geneva, 2012 04/2012 Regulation of Global Broadband Satellite Communications April 2012 . This report has been prepared for ITU by Rajesh Mehrotra, Founder and Principal Consultant, Red Books. The report benefited from extensive review and guidance from the team of the Regulatory and Market Environment Division (RME) of the Telecommunication Development Bureau (BDT). ITU wishes to express thanks to John Alden for editing the paper and to the International Telecommunications Satellite Organization (ITSO) for their comments and advice. This report is part of a new series of ITU reports on broadband that are available online and free of charge at the ITU Universe of Broadband portal: www.itu.int/broadband. Please consider the environment before printing this report. ITU 2012 All rights reserved. No part of this publication may be reproduced, by any means whatsoever, without the prior written permission of ITU. Regulation of global broadband satellite communications Table of Contents Page Preface .......................................................................................................................................... iii Foreword .....................................................................................................................................
    [Show full text]
  • Geosynchronous Satellite Use of GPS
    Geosynchronous Satellite Use of GPS Jennifer L. Ruiz, Lockheed Martin Corporation-Integrated Systems and Solutions Charles H. Frey, Lockheed Martin Corporation-Integrated Systems and Solutions BIOGRAPHY antenna gain patterns, and GPS receiver clock stability on position and timing accuracies at GEO. Jennifer Ruiz is a Systems Engineer for the Lockheed INTRODUCTION Martin Corporation. She received her Bachelor of Science Degree in Electrical Engineering from the GPS missions at GEO synchronous altitude use the University of Delaware and is currently pursuing her spillover of the earth coverage GPS signals. The main M.S.E.E. at Villanova University. She has supported beam of the GPS antenna varies from approximately 23° several programs at Lockheed Martin that use GPS to 26° depending on the Block and frequency of the GPS technology as a means of navigation and is currently vehicle. In addition to the main earth coverage beam, the supporting the GPS III program in the areas of Integrity GPS vehicles have side-lobe signals which have enough and Position, Velocity, and Timing (PVT) system power to reach a user at GEO altitude. Unlike a requirements. Terrestrial User or a Low Earth Orbit (LEO) user of GPS, the GPS satellites a GEO satellite will use are beneath the Chuck Frey is a Senior Staff Systems Engineer with GEO satellite. An illustration of this is given in Figure 1. Lockheed Martin. He holds a Bachelor of Science Degree in Aerospace Engineering from the Pennsylvania State University and a Masters of Science Degree in Side Mechanical Engineering from Villanova University. lobe Chuck developed the suite of tools, Precise Real-time Orbits (PRO) capable of ground or orbit determination which was used for this analysis.
    [Show full text]