User's Guide for SNOPT Version 7.5: Software for Large-Scale Nonlinear
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

University of California, San Diego
UNIVERSITY OF CALIFORNIA, SAN DIEGO Computational Methods for Parameter Estimation in Nonlinear Models A dissertation submitted in partial satisfaction of the requirements for the degree Doctor of Philosophy in Physics with a Specialization in Computational Physics by Bryan Andrew Toth Committee in charge: Professor Henry D. I. Abarbanel, Chair Professor Philip Gill Professor Julius Kuti Professor Gabriel Silva Professor Frank Wuerthwein 2011 Copyright Bryan Andrew Toth, 2011 All rights reserved. The dissertation of Bryan Andrew Toth is approved, and it is acceptable in quality and form for publication on microfilm and electronically: Chair University of California, San Diego 2011 iii DEDICATION To my grandparents, August and Virginia Toth and Willem and Jane Keur, who helped put me on a lifelong path of learning. iv EPIGRAPH An Expert: One who knows more and more about less and less, until eventually he knows everything about nothing. |Source Unknown v TABLE OF CONTENTS Signature Page . iii Dedication . iv Epigraph . v Table of Contents . vi List of Figures . ix List of Tables . x Acknowledgements . xi Vita and Publications . xii Abstract of the Dissertation . xiii Chapter 1 Introduction . 1 1.1 Dynamical Systems . 1 1.1.1 Linear and Nonlinear Dynamics . 2 1.1.2 Chaos . 4 1.1.3 Synchronization . 6 1.2 Parameter Estimation . 8 1.2.1 Kalman Filters . 8 1.2.2 Variational Methods . 9 1.2.3 Parameter Estimation in Nonlinear Systems . 9 1.3 Dissertation Preview . 10 Chapter 2 Dynamical State and Parameter Estimation . 11 2.1 Introduction . 11 2.2 DSPE Overview . 11 2.3 Formulation . 12 2.3.1 Least Squares Minimization . -

Click to Edit Master Title Style
Click to edit Master title style MINLP with Combined Interior Point and Active Set Methods Jose L. Mojica Adam D. Lewis John D. Hedengren Brigham Young University INFORM 2013, Minneapolis, MN Presentation Overview NLP Benchmarking Hock-Schittkowski Dynamic optimization Biological models Combining Interior Point and Active Set MINLP Benchmarking MacMINLP MINLP Model Predictive Control Chiller Thermal Energy Storage Unmanned Aerial Systems Future Developments Oct 9, 2013 APMonitor.com APOPT.com Brigham Young University Overview of Benchmark Testing NLP Benchmark Testing 1 1 2 3 3 min J (x, y,u) APOPT , BPOPT , IPOPT , SNOPT , MINOS x Problem characteristics: s.t. 0 f , x, y,u t Hock Schittkowski, Dynamic Opt, SBML 0 g(x, y,u) Nonlinear Programming (NLP) Differential Algebraic Equations (DAEs) 0 h(x, y,u) n m APMonitor Modeling Language x, y u MINLP Benchmark Testing min J (x, y,u, z) 1 1 2 APOPT , BPOPT , BONMIN x s.t. 0 f , x, y,u, z Problem characteristics: t MacMINLP, Industrial Test Set 0 g(x, y,u, z) Mixed Integer Nonlinear Programming (MINLP) 0 h(x, y,u, z) Mixed Integer Differential Algebraic Equations (MIDAEs) x, y n u m z m APMonitor & AMPL Modeling Language 1–APS, LLC 2–EPL, 3–SBS, Inc. Oct 9, 2013 APMonitor.com APOPT.com Brigham Young University NLP Benchmark – Summary (494) 100 90 80 APOPT+BPOPT APOPT 70 1.0 BPOPT 1.0 60 IPOPT 3.10 IPOPT 50 2.3 SNOPT Percentage (%) 6.1 40 Benchmark Results MINOS 494 Problems 5.5 30 20 10 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 Not worse than 2 times slower than -

Specifying “Logical” Conditions in AMPL Optimization Models
Specifying “Logical” Conditions in AMPL Optimization Models Robert Fourer AMPL Optimization www.ampl.com — 773-336-AMPL INFORMS Annual Meeting Phoenix, Arizona — 14-17 October 2012 Session SA15, Software Demonstrations Robert Fourer, Logical Conditions in AMPL INFORMS Annual Meeting — 14-17 Oct 2012 — Session SA15, Software Demonstrations 1 New and Forthcoming Developments in the AMPL Modeling Language and System Optimization modelers are often stymied by the complications of converting problem logic into algebraic constraints suitable for solvers. The AMPL modeling language thus allows various logical conditions to be described directly. Additionally a new interface to the ILOG CP solver handles logic in a natural way not requiring conventional transformations. Robert Fourer, Logical Conditions in AMPL INFORMS Annual Meeting — 14-17 Oct 2012 — Session SA15, Software Demonstrations 2 AMPL News Free AMPL book chapters AMPL for Courses Extended function library Extended support for “logical” conditions AMPL driver for CPLEX Opt Studio “Concert” C++ interface Support for ILOG CP constraint programming solver Support for “logical” constraints in CPLEX INFORMS Impact Prize to . Originators of AIMMS, AMPL, GAMS, LINDO, MPL Awards presented Sunday 8:30-9:45, Conv Ctr West 101 Doors close 8:45! Robert Fourer, Logical Conditions in AMPL INFORMS Annual Meeting — 14-17 Oct 2012 — Session SA15, Software Demonstrations 3 AMPL Book Chapters now free for download www.ampl.com/BOOK/download.html Bound copies remain available purchase from usual -
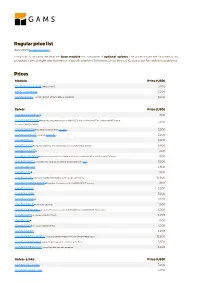
Standard Price List
Regular price list April 2021 (Download PDF ) This price list includes the required base module and a number of optional solvers. The prices shown are for unrestricted, perpetual named single user licenses on a specific platform (Windows, Linux, Mac OS X), please ask for additional platforms. Prices Module Price (USD) GAMS/Base Module (required) 3,200 MIRO Connector 3,200 GAMS/Secure - encrypted Work Files Option 3,200 Solver Price (USD) GAMS/ALPHAECP 1 1,600 GAMS/ANTIGONE 1 (requires the presence of a GAMS/CPLEX and a GAMS/SNOPT or GAMS/CONOPT license, 3,200 includes GAMS/GLOMIQO) GAMS/BARON 1 (for details please follow this link ) 3,200 GAMS/CONOPT (includes CONOPT 4 ) 3,200 GAMS/CPLEX 9,600 GAMS/DECIS 1 (requires presence of a GAMS/CPLEX or a GAMS/MINOS license) 9,600 GAMS/DICOPT 1 1,600 GAMS/GLOMIQO 1 (requires presence of a GAMS/CPLEX and a GAMS/SNOPT or GAMS/CONOPT license) 1,600 GAMS/IPOPTH (includes HSL-routines, for details please follow this link ) 3,200 GAMS/KNITRO 4,800 GAMS/LGO 2 1,600 GAMS/LINDO (includes GAMS/LINDOGLOBAL with no size restrictions) 12,800 GAMS/LINDOGLOBAL 2 (requires the presence of a GAMS/CONOPT license) 1,600 GAMS/MINOS 3,200 GAMS/MOSEK 3,200 GAMS/MPSGE 1 3,200 GAMS/MSNLP 1 (includes LSGRG2) 1,600 GAMS/ODHeuristic (requires the presence of a GAMS/CPLEX or a GAMS/CPLEX-link license) 3,200 GAMS/PATH (includes GAMS/PATHNLP) 3,200 GAMS/SBB 1 1,600 GAMS/SCIP 1 (includes GAMS/SOPLEX) 3,200 GAMS/SNOPT 3,200 GAMS/XPRESS-MINLP (includes GAMS/XPRESS-MIP and GAMS/XPRESS-NLP) 12,800 GAMS/XPRESS-MIP (everything but general nonlinear equations) 9,600 GAMS/XPRESS-NLP (everything but discrete variables) 6,400 Solver-Links Price (USD) GAMS/CPLEX Link 3,200 GAMS/GUROBI Link 3,200 Solver-Links Price (USD) GAMS/MOSEK Link 1,600 GAMS/XPRESS Link 3,200 General information The GAMS Base Module includes the GAMS Language Compiler, GAMS-APIs, and many utilities . -

GEKKO Documentation Release 1.0.1
GEKKO Documentation Release 1.0.1 Logan Beal, John Hedengren Aug 31, 2021 Contents 1 Overview 1 2 Installation 3 3 Project Support 5 4 Citing GEKKO 7 5 Contents 9 6 Overview of GEKKO 89 Index 91 i ii CHAPTER 1 Overview GEKKO is a Python package for machine learning and optimization of mixed-integer and differential algebraic equa- tions. It is coupled with large-scale solvers for linear, quadratic, nonlinear, and mixed integer programming (LP, QP, NLP, MILP, MINLP). Modes of operation include parameter regression, data reconciliation, real-time optimization, dynamic simulation, and nonlinear predictive control. GEKKO is an object-oriented Python library to facilitate local execution of APMonitor. More of the backend details are available at What does GEKKO do? and in the GEKKO Journal Article. Example applications are available to get started with GEKKO. 1 GEKKO Documentation, Release 1.0.1 2 Chapter 1. Overview CHAPTER 2 Installation A pip package is available: pip install gekko Use the —-user option to install if there is a permission error because Python is installed for all users and the account lacks administrative priviledge. The most recent version is 0.2. You can upgrade from the command line with the upgrade flag: pip install--upgrade gekko Another method is to install in a Jupyter notebook with !pip install gekko or with Python code, although this is not the preferred method: try: from pip import main as pipmain except: from pip._internal import main as pipmain pipmain(['install','gekko']) 3 GEKKO Documentation, Release 1.0.1 4 Chapter 2. Installation CHAPTER 3 Project Support There are GEKKO tutorials and documentation in: • GitHub Repository (examples folder) • Dynamic Optimization Course • APMonitor Documentation • GEKKO Documentation • 18 Example Applications with Videos For project specific help, search in the GEKKO topic tags on StackOverflow. -

Largest Small N-Polygons: Numerical Results and Conjectured Optima
Largest Small n-Polygons: Numerical Results and Conjectured Optima János D. Pintér Department of Industrial and Systems Engineering Lehigh University, Bethlehem, PA, USA [email protected] Abstract LSP(n), the largest small polygon with n vertices, is defined as the polygon of unit diameter that has maximal area A(n). Finding the configuration LSP(n) and the corresponding A(n) for even values n 6 is a long-standing challenge that leads to an interesting class of nonlinear optimization problems. We present numerical solution estimates for all even values 6 n 80, using the AMPL model development environment with the LGO nonlinear solver engine option. Our results compare favorably to the results obtained by other researchers who solved the problem using exact approaches (for 6 n 16), or general purpose numerical optimization software (for selected values from the range 6 n 100) using various local nonlinear solvers. Based on the results obtained, we also provide a regression model based estimate of the optimal area sequence {A(n)} for n 6. Key words Largest Small Polygons Mathematical Model Analytical and Numerical Solution Approaches AMPL Modeling Environment LGO Solver Suite For Nonlinear Optimization AMPL-LGO Numerical Results Comparison to Earlier Results Regression Model Based Optimum Estimates 1 Introduction The diameter of a (convex planar) polygon is defined as the maximal distance among the distances measured between all vertex pairs. In other words, the diameter of the polygon is the length of its longest diagonal. The largest small polygon with n vertices is the polygon of unit diameter that has maximal area. For any given integer n 3, we will refer to this polygon as LSP(n) with area A(n). -

Users Guide for Snadiopt: a Package Adding Automatic Differentiation to Snopt∗
USERS GUIDE FOR SNADIOPT: A PACKAGE ADDING AUTOMATIC DIFFERENTIATION TO SNOPT∗ E. Michael GERTZ Mathematics and Computer Science Division Argonne National Laboratory Argonne, Illinois 60439 Philip E. GILL and Julia MUETHERIG Department of Mathematics University of California, San Diego La Jolla, California 92093-0112 January 2001 Abstract SnadiOpt is a package that supports the use of the automatic differentiation package ADIFOR with the optimization package Snopt. Snopt is a general-purpose system for solving optimization problems with many variables and constraints. It minimizes a linear or nonlinear function subject to bounds on the variables and sparse linear or nonlinear constraints. It is suitable for large-scale linear and quadratic programming and for linearly constrained optimization, as well as for general nonlinear programs. The method used by Snopt requires the first derivatives of the objective and con- straint functions to be available. The SnadiOpt package allows users to avoid the time- consuming and error-prone process of evaluating and coding these derivatives. Given Fortran code for evaluating only the values of the objective and constraints, SnadiOpt automatically generates the code for evaluating the derivatives and builds the relevant Snopt input files and sparse data structures. Keywords: Large-scale nonlinear programming, constrained optimization, SQP methods, automatic differentiation, Fortran software. [email protected] [email protected] [email protected] http://www.mcs.anl.gov/ gertz/ http://www.scicomp.ucsd.edu/ peg/ http://www.scicomp.ucsd.edu/ julia/ ∼ ∼ ∼ ∗Partially supported by National Science Foundation grant CCR-95-27151. Contents 1. Introduction 3 1.1 Problem Types . 3 1.2 Why Automatic Differentiation? . 3 1.3 ADIFOR ...................................... -

The Optimization Module User's Guide
Optimization Module User’s Guide Optimization Module User’s Guide © 1998–2018 COMSOL Protected by patents listed on www.comsol.com/patents, and U.S. Patents 7,519,518; 7,596,474; 7,623,991; 8,457,932; 8,954,302; 9,098,106; 9,146,652; 9,323,503; 9,372,673; and 9,454,625. Patents pending. This Documentation and the Programs described herein are furnished under the COMSOL Software License Agreement (www.comsol.com/comsol-license-agreement) and may be used or copied only under the terms of the license agreement. COMSOL, the COMSOL logo, COMSOL Multiphysics, COMSOL Desktop, COMSOL Server, and LiveLink are either registered trademarks or trademarks of COMSOL AB. All other trademarks are the property of their respective owners, and COMSOL AB and its subsidiaries and products are not affiliated with, endorsed by, sponsored by, or supported by those trademark owners. For a list of such trademark owners, see www.comsol.com/trademarks. Version: COMSOL 5.4 Contact Information Visit the Contact COMSOL page at www.comsol.com/contact to submit general inquiries, contact Technical Support, or search for an address and phone number. You can also visit the Worldwide Sales Offices page at www.comsol.com/contact/offices for address and contact information. If you need to contact Support, an online request form is located at the COMSOL Access page at www.comsol.com/support/case. Other useful links include: • Support Center: www.comsol.com/support • Product Download: www.comsol.com/product-download • Product Updates: www.comsol.com/support/updates • COMSOL Blog: www.comsol.com/blogs • Discussion Forum: www.comsol.com/community • Events: www.comsol.com/events • COMSOL Video Gallery: www.comsol.com/video • Support Knowledge Base: www.comsol.com/support/knowledgebase Part number: CM021701 Contents Chapter 1: Introduction Optimization Module Overview 8 What Can the Optimization Module Do?. -

Clean Sky – Awacs Final Report
Clean Sky Joint Undertaking AWACs – Adaptation of WORHP to Avionics Constraints Clean Sky – AWACs Final Report Table of Contents 1 Executive Summary ......................................................................................................................... 2 2 Summary Description of Project Context and Objectives ............................................................... 3 3 Description of the main S&T results/foregrounds .......................................................................... 5 3.1 Analysis of Optimisation Environment .................................................................................... 5 3.1.1 Problem sparsity .............................................................................................................. 6 3.1.2 Certification aspects ........................................................................................................ 6 3.2 New solver interfaces .............................................................................................................. 6 3.3 Conservative iteration mode ................................................................................................... 6 3.4 Robustness to erroneous inputs ............................................................................................. 7 3.5 Direct multiple shooting .......................................................................................................... 7 3.6 Grid refinement ...................................................................................................................... -

Optimal Control for Constrained Hybrid System Computational Libraries and Applications
FINAL REPORT: FEUP2013.LTPAIVA.01 Optimal Control for Constrained Hybrid System Computational Libraries and Applications L.T. Paiva 1 1 Department of Electrical and Computer Engineering University of Porto, Faculty of Engineering - Rua Dr. Roberto Frias, s/n, 4200–465 Porto, Portugal ) [email protected] % 22 508 1450 February 28, 2013 Abstract This final report briefly describes the work carried out under the project PTDC/EEA- CRO/116014/2009 – “Optimal Control for Constrained Hybrid System”. The aim was to build and maintain a software platform to test an illustrate the use of the conceptual tools developed during the overall project: not only in academic examples but also in case studies in the areas of robotics, medicine and exploitation of renewable resources. The grand holder developed a critical hands–on knowledge of the available optimal control solvers as well as package based on non–linear programming solvers. 1 2 Contents 1 OC & NLP Interfaces 7 1.1 Introduction . .7 1.2 AMPL . .7 1.3 ACADO – Automatic Control And Dynamic Optimization . .8 1.4 BOCOP – The optimal control solver . .9 1.5 DIDO – Automatic Control And Dynamic Optimization . 10 1.6 ICLOCS – Imperial College London Optimal Control Software . 12 1.7 TACO – Toolkit for AMPL Control Optimization . 12 1.8 Pseudospectral Methods in Optimal Control . 13 2 NLP Solvers 17 2.1 Introduction . 17 2.2 IPOPT – Interior Point OPTimizer . 17 2.3 KNITRO . 25 2.4 WORHP – WORHP Optimises Really Huge Problems . 31 2.5 Other Commercial Packages . 33 3 Project webpage 35 4 Optimal Control Toolbox 37 5 Applications 39 5.1 Car–Like . -

Landing Trajectory Optimization for the Robobee
Landing Trajectory Optimization for the RoboBee Rebecca Steinmeyer Irina Tolkova Harvard University Harvard University [email protected] [email protected] Abstract The Harvard RoboBee is an insect-scale flapping-wing micro-aerial vehicle, subject to extreme challenges in maneuvering due to its small scale and control authority, and inherent instability. Landing the vehicle, in particular, remains an unsolved problem (and is typically bypassed during experiments); determining an optimal landing trajectory would increase system versatility. We sought to apply optimiza- tion techniques to determine control inputs (forces and torques) for trajectories which result in a desired final position and orientation (from a variety of initial states), using IPOPT, SNOPT, and an ADMM-based method. Furthermore, we found optimal wingstroke signal parameters to produce the resulting control inputs, both by expansion of the initial optimization methods and by separate implementa- tion of Projected Gradient Descent. We found that all three solvers were able to achieve physically feasible control parameters for the landing problem with similar degrees of optimality. We compare the advantages and challenges of each solver and problem formulation for trajectory optimization of the RoboBee. 1 Introduction The Harvard RoboBee is an 87 mg flapping-wing micro-aerial vehicle (MAV) which achieves flight via two independently flapping wings [16], each actuated by its own piezoelectric bimorph actuator [17]. The MAV is characterized by a resonant flapping -

Open Source and Free Software
WP. 24 ENGLISH ONLY UNITED NATIONS STATISTICAL COMMISSION and EUROPEAN COMMISSION ECONOMIC COMMISSION FOR EUROPE STATISTICAL OFFICE OF THE CONFERENCE OF EUROPEAN STATISTICIANS EUROPEAN COMMUNITIES (EUROSTAT) Joint UNECE/Eurostat work session on statistical data confidentiality (Bilbao, Spain, 2-4 December 2009) Topic (iv): Tools and software improvements ON OPEN SOURCE SOFTWARE FOR STATISTICAL DISCLOSURE LIMITATION Invited Paper Prepared by Juan José Salazar González, University of La Laguna, Spain On open source software for Statistical Disclosure Limitation Juan José Salazar González * * Department of Statistics, Operations Research and Computer Science, University of La Laguna, 38271 Tenerife, Spain, e-mail: [email protected] Abstract: Much effort has been done in the last years to design, analyze, implement and compare different methodologies to ensure confidentiality during data publication. The knowledge of these methods is public, but the practical implementations are subject to different license constraints. This paper summarizes some concepts on free and open source software, and gives some light on the convenience of using these schemes when building automatic tools in Statistical Disclosure Limitation. Our results are based on some computational experiments comparing different mathematical programming solvers when applying controlled rounding to tabular data. 1 Introduction Statistical agencies must guarantee confidentiality of data respondent by using the best of modern technology. Today data snoopers may have powerful computers, thus statistical agencies need sophisticated computer programs to ensure that released information is protected against attackers. Recent research has designed different optimization techniques that ensure protection. Unfortunately the number of users of these techniques is quite small (mainly national and regional statistical agencies), thus there is not enough market to stimulate the development of several implementations, all competing for being the best.