DOCSLIB.ORG

Natural Selection

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Natural Selection Natural Selection Evolution by natural selection Natural selection requires phenotypic variation Selection occurs if variation in fitness is associated with variation in the phenotype (i.e., there is a covariance between fitness and phenotype) Evolution by natural selection can occur if part of the phenotypic variance is heritable (i.e., there is a covariance between phenotype and genotype) 1 Evolution by natural selection Directional Selection (change in population mean and reduction in VA) Non-linear Selection (stabilizing) (reduction in VA) Non-linear Selection (disruptive) (increase in VA) Prediction: Selection reduces the standing genetic variation in populations Collared flycatcher (Ficedula albicollis) Gustaffson (1986) 2 Prediction: Selection reduces the standing genetic variation in populations Across species comparison Roff (1997) Maintenance of heritable variation EquilibriumEquilibrium betweenbetween newlynewly emergingemerging geneticgenetic variabilityvariability andand selectionselection removingremoving geneticgenetic variantsvariants fromfrom thethe population.population. Population-,Population-, interindividualinterindividual variability variability Mutation Selection Migration 3 Directional Selection Selection differential: Covariance between fitness and phenotype The „Price Equation“ (Price, 1970) („Robertson-Price Identity“: Lynch and Walsh,1998) 2 Δzi = cov(wi , zi ) = h S = βVa = βG Δz = evolutionary change from generation t to t+1 (equivalent to R in breeders equation) i = index-subscript for a particular phenotype/trait β = selection gradient (slightly different from selection differential) G = additive genetic variance (equivalent to VA) ⎛W ⎞ w = relative fitness ⎜ i ⎟ i ⎝W⎠ Directional Selection Linear Regression Directional Selection differential (S): within-generational difference y = a + bx between mean phenotype after episode of selection (but before reproduction) and the mean before the selection episode (sometimes: Linear Fitness Equation “total selection”). Equivalent to w regression of relative fitness on phenotype. Only for directional selection. w = a + βz Selection gradient (β, γ): partial regression coefficients of relative z fitness on a given trait (sometimes: a: baseline fitness “direct selection”). For directional, β: directional selection gradient non-linear and correlational z: phenotypic trait selection. 4 Directional Selection V G S R = h2S = a S = S = G = Gβ univariate Vp P P Δz = GP−1S = Gβ multivariate hence −1 S ⎯⎯→⎯ β = P S = (the bold upright font P indicates matrix notation) Non-linear Selection Quadratic Regression y = a + bx + cx2 1 Non-linear fitness equation 0.8 1 0.6 w = a + βx + γx2 0.4 2 0.2 2 4 6 8 10 Linear component Non-linear (quadratic) (gradient) component (gradient) The non-linear selection gradient does not directly affect the change in the phenotypic mean from one generation to the next (Δz ). But it affect the genetic co-/variances. Lande & Arnold 1983 5 Evolution by natural selection Of selective targets PhenotypicPhenotypic traitraitt underunder selectionselection and agents Ecological/socialEcological/social factorfactor thatthat generatesgenerates aa covariancecovariance betweenbetween fitnessfitness andand phenotypephenotype Evolution by natural selection Agent 001 = Agent 002 = parasitoid Bird predation Goldenrod = Goldrute (Target) Eurosta gall fly 6 Example non-linear Selection Stabilizing selection? Goldenrod = Goldrute Eurosta fly Eurosta gall Eurosta gall fly Directional and Stabilizing Selection Fitness function Phenotype distribution in the population StabilizingStabilizing andand directionaldirectional selectionselection areare notnot mutuallymutually exclusiveexclusive 7 Directional and Stabilizing Selection Fitness function Phenotype distributions in the population β = 0 β > 0 β > 0 β = 0 β < 0 γ = 0 γ = 0 γ < 0 γ < 0 γ ≥ 0 w Phenotypic trait value Natural/Sexual Selection Experimental Design 8 Definitions of Fitness • Strict definition: A genotype‘s rate of increase in a population (e.g. Futuyma 1986) • Working definitions: • Fitness components 1. Individual survival (longevity) 2. Fecundity (clutch size, hatching success, number of surviving offspring, number or reproducing offspring, fedundity of offspring, number of grand-children, ...) 3. Insemination rate 4. .... Often specific to the biology of the study organism. Example: Estimating selection differentials and gradients Fitness (lifetime nr. of nr. of (lifetime inseminations) Horn length (mm) Elytra length (mm) Fungus beetle Bolithotherus cornutus 9 OnOn thethe „+“„+“ side side •• Selection Selection isis observedobserved asas itit isis actuallyactually „happening“„happening“ in in thethe populationpopulation •• Estimation Estimation ofof indirectindirect selectionselection OnOn thethe „-“„-“ side side •• It It isis notnot possiblepossible toto bebe completelycompletely suresure toto havehave causallycausally isolatedisolated thethe „target„target ofof selection“selection“** •• It It isis difficultdifficult toto inferinfer thethe „agents„agents ofof selection“selection“ causally causally** *The problem of third variable causation (e.g., Ruxton and Colgrave, 2006) Example: Experimentally testing targets of selection Long-tailed widow bird S C L (Euplectes progne) Anderson 1982. Nature 299, 818-820 10 OnOn thethe „+“„+“ side side •• Causal Causal identificationidentification ofof targettarget ofof selectionselection (manipulation(manipulation ofof targettarget trait)trait) •• Causal Causal identificationidentification ofof agentagent ofof selectionselection (manipulation(manipulation ofof ecologicalecological factor)factor) OnOn thethe „-“„-“ side side •• Univariate Univariate approach,approach, usuallyusually oneone traittrait atat aa timetime •• Not Not allall traitstraits cancan bebe easilyeasily andand directlydirectly manipulatedmanipulated •• Risk Risk ofof generatinggenerating exaggeratedexaggerated („unnatural“)(„unnatural“) variancevariance inin thethe traittrait →→ CAREFULCAREFUL experimentationexperimentation requiredrequired It can be interesting to experimentally create phenotypes that are outside the natural range Experimental extreme values w Phenotypic trait value Example: sensory biases in the evolution of communication/signalling 11 Zebra finch (Taenopygia guttata) Male Attractiveness Female Attractiveness Of 49 offspring reaching adulthood, 29 were reared by males with red colour bands, and 36 had mothers with orange bands. Burley 1981, Science Note on fitness components •• In In evolutionaryevolutionary andand behaviouralbehavioural ecology,ecology, fitnessfitness componentscomponents areare oftenoften partitionedpartitioned intointo a benefit part andand aa costcost partpart •• Benefits Benefits andand costscosts areare oftenoften investigatedinvestigated separatelyseparately •• But: But: whatwhat mattersmatters isis thethe life-timelife-time valuevalue forfor thethe componentcomponent (trade-offs(trade-offs involved)involved) Does this result mean that there is ongoing directional selection on male tail length in these widowbirds? 12 Note on fitness components 0.5 0.4 0.3 : Fitness 0.2 W 0.1 S2 CL4 6 8 10 Phenotype Benefit part of fitness component Cost part of fitness component (e.g., mating success, nr nests) (e.g., survival probability) 1 1 0.8 0.8 0.6 0.6 0.4 0.4 0.2 0.2 SCL2 4 6 8 10 SCL2 4 6 8 10 13.
Load more

Recommended publications
  • An Introgression Analysis of Quantitative Trait Loci That Contribute to a Morphological Difference Between Drosophila Simulans and D
    Copyight 0 1997 by the Genetics Societv of America An Introgression Analysis of Quantitative Trait Loci That Contribute to a Morphological Difference Between Drosophila simulans and D. mauritiana Cathy C. Laurie, John R. True, Jianjun Liu and John M. Mercer Department of Zoology, Duke University, Durham, North Carolina 27708 Manuscript received August 12, 1996 Accepted for publication October 29, 1996 ABSTRACT Drosophila simulans and D. maum'tiana differ markedly in morphology of the posterior lobe, a male- specific genitalic structure. Bothsize and shapeof the lobe can be quantifiedby a morphometric variable, PC1, derived from principal components and Fourier analyses. The genetic architectureof the species difference in PC1 was investigated previously by composite interval mapping, which revealed largely additive inheritance, with a minimum of eight quantitative trait loci (QTL) affecting the trait. This analysis was extended by introgression of marked segments of the maun'tiana third chromosome into a simulans background by repeated backcrossing. Thetwo types of experiment are consistentin suggesting that several QTL on the third chromosome may have effects in the range of 10-15% of the parental difference andthat all or nearly all QTL have effects in the same direction. Since the parental difference is large (30.4 environmental standard deviations), effects of this magnitude can produce alternative homozygotes with little overlap in phenotype. However, these estimates may not reflect the effects of individual loci, since each interval or introgressed segment may contain multiple QTL. The consistent direction of allelic effects suggests a history of directional selection on the posterior lobe. HE genetic analysis of a quantitative trait usually ual genes that affect continuously variable traits.
    [Show full text]
  • Natural Selection on Phenotypes
    Conner and Hartl – p. 6-1 From: Conner, J. and D. Hartl, A Primer of Ecological Genetics. In prep. for Sinauer Chapter 6: Natural selection on phenotypes Natural selection and adaptation have been recurring themes throughout this book, from the very beginning of chapter 1. We discussed selection on genotypes (and discrete phenotypes) in chapter 3, and now that we have a good understanding of the genetics of continuously distributed traits we turn to selection on these common and ecologically important phenotypes. We discuss the very general and widely used regression-based approaches to measuring selection, and cover ways to identify the phenotypic traits that are the direct targets of selection, as well as ways to determine the environmental agents that are causing selection. Identifying selective agents and targets is a powerful approach to understanding adaptation. Finally, we integrate this material with the concepts covered in chapters 4 and 5 to show how short-term phenotypic evolution can be modeled and predicted, and how this undertaking sheds light on constraints on adaptive evolution. Throughout the chapter the effects of genetic and phenotypic correlations among traits are highlighted. Evolution by natural selection has three parts (Figure 6.1; Endler 1986): 1. There is phenotypic variation for the trait of interest. 2. There is some consistent relationship between this phenotypic variation and variation in fitness. 3. A significant proportion of the phenotypic variation is caused by additive genetic variance, that is, the trait is heritable. Numbers 1 and 2 represent selection on phenotypes, which occurs within a generation and can be quantified using the selection differential (S) just as with artificial selection.
    [Show full text]
  • Microevolution and the Genetics of Populations ​ ​ Microevolution Refers to Varieties Within a Given Type
    Chapter 8: Evolution Lesson 8.3: Microevolution and the Genetics of Populations ​ ​ Microevolution refers to varieties within a given type. Change happens within a group, but the descendant is clearly of the same type as the ancestor. This might better be called variation, or adaptation, but the changes are "horizontal" in effect, not "vertical." Such changes might be accomplished by "natural selection," in which a trait ​ ​ ​ ​ within the present variety is selected as the best for a given set of conditions, or accomplished by "artificial selection," such as when dog breeders produce a new breed of dog. Lesson Objectives ● Distinguish what is microevolution and how it affects changes in populations. ● Define gene pool, and explain how to calculate allele frequencies. ● State the Hardy-Weinberg theorem ● Identify the five forces of evolution. Vocabulary ● adaptive radiation ● gene pool ● migration ● allele frequency ● genetic drift ● mutation ● artificial selection ● Hardy-Weinberg theorem ● natural selection ● directional selection ● macroevolution ● population genetics ● disruptive selection ● microevolution ● stabilizing selection ● gene flow Introduction Darwin knew that heritable variations are needed for evolution to occur. However, he knew nothing about Mendel’s laws of genetics. Mendel’s laws were rediscovered in the early 1900s. Only then could scientists fully understand the process of evolution. Microevolution is how individual traits within a population change over time. In order for a population to change, some things must be assumed to be true. In other words, there must be some sort of process happening that causes microevolution. The five ways alleles within a population change over time are natural selection, migration (gene flow), mating, mutations, or genetic drift.
    [Show full text]
  • Directional Selection and Variation in Finite Populations
    Copyright 0 1987 by the Genetics Society of America Directional Selection and Variation in Finite Populations Peter D. Keightley and ‘William G. Hill Institute of Animal Genetics, University of Edinburgh, West Mains Road, Edinburgh EH9 3JN, Scotland Manuscript received April 12, 1987 Revised copy accepted July 16, 1987 ABSTRACT Predictions are made of the equilibrium genetic variances and responses in a metric trait under the joint effects of directional selection, mutation and linkage in a finite population. The “infinitesimal model“ is analyzed as the limiting case of many mutants of very small effect, otherwise Monte Carlo simulation is used. If the effects of mutant genes on the trait are symmetrically distributed and they are unlinked, the variance of mutant effects is not an important parameter. If the distribution is skewed, unless effects or the population size is small, the proportion of mutants that have increasing effect is the critical parameter. With linkage the distribution of genotypic values in the population becomes skewed downward and the equilibrium genetic variance and response are smaller as disequilibrium becomes important. Linkage effects are greater when the mutational variance is contributed by many genes of small effect than few of large effect, and are greater when the majority of mutants increase rather than decrease the trait because genes that are of large effect or are deleterious do not segregate for long. The most likely conditions for ‘‘Muller’s ratchet” are investi- gated. N recent years there has been much interest in the is attained more quickly in the presence of selection I production and maintenance of variation in pop- than in its absence, and is highly dependent on popu- ulations by mutation, stimulated by the presence of lation size.
    [Show full text]
  • Patterns and Power of Phenotypic Selection in Nature
    Articles Patterns and Power of Phenotypic Selection in Nature JOEL G. KINGSOLVER AND DAVID W. PFENNIG Phenotypic selection occurs when individuals with certain characteristics produce more surviving offspring than individuals with other characteristics. Although selection is regarded as the chief engine of evolutionary change, scientists have only recently begun to measure its action in the wild. These studies raise numerous questions: How strong is selection, and do different types of traits experience different patterns of selection? Is selection on traits that affect mating success as strong as selection on traits that affect survival? Does selection tend to favor larger body size, and, if so, what are its consequences? We explore these questions and discuss the pitfalls and future prospects of measuring selection in natural populations. Keywords: adaptive landscape, Cope’s rule, natural selection, rapid evolution, sexual selection henotypic selection occurs when individuals with selection on traits that affect survival stronger than on those Pdifferent characteristics (i.e., different phenotypes) that affect only mating success? In this article, we explore these differ in their survival, fecundity, or mating success. The idea and other questions about the patterns and power of phe- of phenotypic selection traces back to Darwin and Wallace notypic selection in nature. (1858), and selection is widely accepted as the primary cause of adaptive evolution within natural populations.Yet Darwin What is selection, and how does it work? never attempted to measure selection in nature, and in the Selection is the nonrandom differential survival or repro- century following the publication of On the Origin of Species duction of phenotypically different individuals.
    [Show full text]
  • Selection and Gene Duplication: a View from the Genome Comment Andreas Wagner
    http://genomebiology.com/2002/3/5/reviews/1012.1 Minireview Selection and gene duplication: a view from the genome comment Andreas Wagner Address: Department of Biology, University of New Mexico, 167A Castetter Hall, Albuquerque, NM 817131-1091, USA. E-mail: [email protected] Published: 15 April 2002 Genome Biology 2002, 3(5):reviews1012.1–1012.3 reviews The electronic version of this article is the complete one and can be found online at http://genomebiology.com/2002/3/5/reviews/1012 © BioMed Central Ltd (Print ISSN 1465-6906; Online ISSN 1465-6914) Abstract reports Immediately after a gene duplication event, the duplicate genes have redundant functions. Is natural selection therefore completely relaxed after duplication? Does one gene evolve more rapidly than the other? Several recent genome-wide studies have suggested that duplicate genes are always under purifying selection and do not always evolve at the same rate. deposited research When a gene duplication event occurs, the duplicate genes synonymous (silent) nucleotide substitutions, Ks, and have redundant functions. Many deleterious mutations may second, of non-synonymous nucleotide substitutions (which then be harmless, because even if one gene suffers a muta- change the encoded amino acid), Ka (see Box 1). The ratio tion, the redundant gene copy can provide a back-up func- Ka/Ks provides a measure of the selection pressure to which tion. Put differently, after gene duplication - which can arise a gene pair is subject. If a duplicate gene pair shows a Ka/Ks through polyploidization (whole-genome duplication), non- ratio of about 1, that is, if amino-acid replacement substitu- homologous recombination, or through the action of retro- tions occur at the same rate as synonymous substitutions, transposons - one or both duplicates should experience then few or no amino-acid replacement substitutions have refereed research relaxed selective constraints that result in elevated rates of been eliminated since the gene duplication.
    [Show full text]
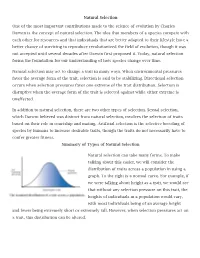
  • Natural Selection One of the Most Important Contributions Made to The
    Natural Selection One of the most important contributions made to the science of evolution by Charles Darwin is the concept of natural selection. The idea that members of a species compete with each other for resources and that individuals that are better adapted to their lifestyle have a better chance of surviving to reproduce revolutionized the field of evolution, though it was not accepted until several decades after Darwin first proposed it. Today, natural selection forms the foundation for our understanding of how species change over time. Natural selection may act to change a trait in many ways. When environmental pressures favor the average form of the trait, selection is said to be stabilizing. Directional selection occurs when selection pressures favor one extreme of the trait distribution. Selection is disruptive when the average form of the trait is selected against while either extreme is unaffected. In addition to natural selection, there are two other types of selection. Sexual selection, which Darwin believed was distinct from natural selection, involves the selection of traits based on their role in courtship and mating. Artificial selection is the selective breeding of species by humans to increase desirable traits, though the traits do not necessarily have to confer greater fitness. Summary of Types of Natural Selection Natural selection can take many forms. To make talking about this easier, we will consider the distribution of traits across a population in using a graph. To the right is a normal curve. For example, if we were talking about height as a trait, we would see that without any selection pressure on this trait, the heights of individuals in a population would vary, with most individuals being of an average height and fewer being extremely short or extremely tall.
    [Show full text]
  • Detecting the Form of Selection from DNA Sequence Data
    Outlook COMMENT Male:female mutation ratio muscular dystrophy, neurofibromatosis and retinoblast- outcome of further investigation, this unique transposition oma), there is a large male excess. So, I believe the evidence event and perhaps others like it are sure to provide impor- is convincing that the male base-substitution rate greatly tant cytogenetic and evolutionary insights. exceeds the female rate. There are a number of reasons why the historical Acknowledgements male:female mutation ratio is likely to be less than the I have profited greatly from discussions with my colleagues current one, the most important being the lower age of B. Dove, B. Engels, C. Denniston and M. Susman. My reproduction in the earliest humans and their ape-like greatest debt is to D. Page for a continuing and very fruitful ancestors. More studies are needed. But whatever the dialog and for providing me with unpublished data. References Nature 406, 622–625 6 Engels, W.R. et al. (1994) Long-range cis preference in DNA 1 Vogel, F. and Motulsky, A. G. (1997) Human Genetics: 4 Shimmin, L.C. et al. (1993) Potential problems in estimating homology search over the length of a Drosophila chromosome. Problems and Approaches. Springer-Verlag the male-to-female mutation rate ratio from DNA sequence Science 263, 1623–1625 2 Crow, J. F. (1997) The high spontaneous mutation rate: is it a data. J. Mol. Evol. 37, 160–166 7 Crow, J.F. (2000) The origins, patterns and implications of health risk? Proc. Natl. Acad. Sci. U. S. A. 94, 8380–8386 5 Richardson, C. et al.
    [Show full text]
  • Mathematics and Biology Have Not Been Easy Bedfellows and There Are
    Mathematics and biology have not been easy bedfellows and there are many ex- amples of biologists who have made terrible mistakes by ignoring mathematics and also mathematicians who have not fared very well when they have dipped their toes in the biological pool. Russ’s work is a great example of the fruitful interaction between the two fi elds and it gives me enormous pleasure to call on him to deliver his lecture. Russell Lande Theoretical Population Biology: (A) Evolution of correlated characters (B) Stochastic demography and conservation (A) Evolution of correlated characters: The fundamental principle of natural selection by which living organisms adapt to their environments was discovered by Darwin (1859), who integrated a wide variety of evidence supporting the theory of evolution. Differences in individual fi tness due to variation among individuals in characters infl uencing survival and reproduction, combined with partial heritability of the variation, causes adaptive evolution. The validity of this theory is strongly confi rmed by modern genetic data. Darwin and the early naturalists understood that natural selection acts simultaneously on many characters of an organism, and that hereditary constraints among characters prevent their independent evolution. On the Origin of Species, Darwin (1859) wrote that when man or nature selects on a given character, that character as well as other correlated characters evolve, due to ‘correla- tion of growth’. We now know that genetic correlations between characters are caused by pleiotropy (a single gene infl uencing multiple characters) and linkage disequilib- rium (nonrandom association between allelic forms of different genes, especially on the same chromosome).
    [Show full text]
  • Supplementary Information for Vyssotski, 2013
    Supplementary Information for Vyssotski, 2013 www.evolocus.com/evolocus/v1/evolocus-01-013-s.pdf Evolocus Supplementary Information for Transgenerational epigenetic compensation and sex u al d imorph ism 1,2,3 Dmitri L. Vyssotski Published 17 May 2013, Evolocus 1, 13-18 (2013): http://www.evolocus.com/evolocus/v1/evolocus-01-013.pdf In natu ral popu lation transgenerational epigenetic compensation is by unknown mechanisms, the mechanisms those were difficult to generated in h omoz y gou s mu tants, mainly in males. It d oes not imagine, and this possibility was abandoned for over 47 years. immed iately affect th e ph enoty pe of h omoz y gou s mu tants, w h ere The higher variability in males can be a result of a not so good it w as generated . Transgenerational epigenetic compensation is canalization of their ontogenesis, and the canalization of localiz ed not in th e same locu s as original mu tation and it is ontogenesis is modulated by sex hormones. Thus, we can d ominant, b ecau se it affects th e ph enoty pe ev en if it is receiv ed imagine that the canalization of ontogenesis in males is from one parent. In fu rth er generations, starting from F 2, it is more artificially decreased in comparison with females by means of ex pressed in females th an in males: it increases fitness of hormonal differences. h omozy gou s mu tant females, d ecreases fitness of w ild ty pe The shift of the female distribution to the right was not females and h as w eak effect on h eterozy gou s females.
    [Show full text]
  • Stabilizing Selection Shapes Variation in Phenotypic Plasticity
    bioRxiv preprint doi: https://doi.org/10.1101/2021.07.29.454146; this version posted July 29, 2021. The copyright holder for this preprint (which was not certified by peer review) is the author/funder. All rights reserved. No reuse allowed without permission. 1 Stabilizing selection shapes variation in phenotypic plasticity 2 3 4 5 Dörthe Becker1,2,*, 6 Karen Barnard-Kubow1,3, 7 Robert Porter1, 8 Austin Edwards1,4, 9 Erin Voss1,5, 10 Andrew P. Beckerman2, 11 Alan O. Bergland1,* 12 13 14 1Department of Biology; University of Virginia, Charlottesville/VA, USA 15 2Department of Animal and Plant Sciences; University of Sheffield, Sheffield, UK 16 3Department of Biology, James Madison University, Harrisonburg/VA, USA 17 4Biological Imaging Development CoLab, University of California San Francisco, 18 San Francisco/CA, USA 19 5Department of Integrative Biology, University of California Berkeley, 20 Berkeley/CA 21 22 * to whom correspondence should be addressed: 23 DB ([email protected]), AOB ([email protected]) 24 25 26 27 Keywords: stabilizing selection; phenotypic plasticity; heritability; Daphnia; 28 defense morphologies 1 bioRxiv preprint doi: https://doi.org/10.1101/2021.07.29.454146; this version posted July 29, 2021. The copyright holder for this preprint (which was not certified by peer review) is the author/funder. All rights reserved. No reuse allowed without permission. 29 Abstract 30 The adaptive nature of phenotypic plasticity is widely documented in natural 31 populations. However, little is known about the evolutionary forces that shape 32 genetic variation in plasticity within populations. Here we empirically address this 33 issue by testing the hypothesis that stabilizing selection shapes genetic variation 34 in the anti-predator developmental plasticity of Daphnia pulex.
    [Show full text]
  • Selection on Breeding Date and Body Size in Colonizing Coho Salmon, Oncorhynchus Kisutch
    Molecular Ecology (2010) 19, 2562–2573 doi: 10.1111/j.1365-294X.2010.04652.x Selection on breeding date and body size in colonizing coho salmon, Oncorhynchus kisutch J. H. ANDERSON,* P. L. FAULDS,† W. I. ATLAS,‡ G. R. PESS§ and T. P. QUINN* *School of Aquatic and Fishery Sciences, University of Washington, Box 355020, Seattle, WA 98195, USA, †Seattle Public Utilities, 700 5th Avenue, Suite 4900, Seattle, WA, 98124, USA, ‡Department of Biological Sciences, Simon Fraser University, 8888 University Drive, Burnaby, BC, Canada V5A 1S6, §National Marine Fisheries Service, Northwest Fisheries Science Center, 2725 Montlake Boulevard East, Seattle, WA 98195, USA Abstract Selection during the colonization of new habitat is critical to the process of local adaptation, but has rarely been studied. We measured the form, direction, and strength of selection on body size and date of arrival to the breeding grounds over the first three cohorts (2003–2005) of a coho salmon (Oncorhynchus kisutch) population colonizing 33 km of habitat made accessible by modification of Landsburg Diversion Dam, on the Cedar River, Washington, USA. Salmon were sampled as they bypassed the dam, parentage was assigned based on genotypes from 10 microsatellite loci, and standardized selection gradients were calculated using the number of returning adult offspring as the fitness metric. Larger fish in both sexes produced more adult offspring, and the magnitude of the effect increased in subsequent years for males, suggesting that low densities attenuated traditional size-biased intrasexual competition. For both sexes, directional selection favoured early breeders in 2003, but stabilizing selection on breeding date was observed in 2004 and 2005.
    [Show full text]