DOCSLIB.ORG

LECTURE 7 : CALCULATING PROPERTIES Space Correlation Functions Radial Distribution Function Structure Factor Coordination Numbers, Angles, Etc

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
LECTURE 7 : CALCULATING PROPERTIES Space Correlation Functions Radial Distribution Function Structure Factor Coordination Numbers, Angles, Etc We have generated sets of (x,y,z) positions for various times at various given thermodynamic conditions (N,V,T,P). Now, we use them. LECTURE 7 : CALCULATING PROPERTIES Space correlation functions Radial distribution function Structure factor Coordination numbers, angles, etc. [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING A) RADIAL DISTRIBUTION FUNCTION ρ (1) ρ (2) Structural caracterization: Probability densities N and N i.e. one can find N particles and N(N-1) pairs of particles in the total volume, respectively. Note that these are n=1 and n=2 cases of a general correlation function g(n) given by : ZN the partition function, V the volume, N the nb of particles [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING So that one can write for e.g. n=2: 2 which defines the radial distribution (rdf) g N (r 1,r 2) function, also given by ρ (1) ρ For an homogeneous isotropic system, one has N = . Dependence of the rdf only on relative distance between particles: So that ρg(r) is the conditional probability to find another particle at a distance r away from the origin. [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING g(r) is the pair correlation function In a simulation box with PBC, one cannot obtain the structure beyond r > L/2. Alternatively: Radial distribution function : 1 () = ( + − ) Pair correlation function: 1 1 () = ( − − ) 4 Alternative definitions : Total distribution function: = 4() Differential distribution function = 4 − 1 [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING Pair distribution function : examples Visual inspection allows to distinguish between a crystalline and an amorphous structure CCP Ni lattice with EAM potential [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING Effect of thermodynamic variables : temperature The integral of g(r) allows to Amorphous Se determine the number of neighbors around a central atom. Remember The integral to the first minimum gives the coordination number. r = 4 m Running coordination number N(r) Caprion, Schober, PRB 2000 () = 4 [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING Effect of thermodynamic variables : pressure d-GeO 2 Direct comparison with experiments can fail Simple force fields can not account for pressure-induced changes (metallization) Additional structural insight is provided by partial correlation functions : Ge-Ge, Ge-O, O-O Expt. (neutron) Salmon, JPCM 2011 MD: 256 GeO 2 using Oeffner-Elliot FF Micoulaut, JPCM 2004 [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING Effect of composition: extending to multicomponent systems This is case for most glasses and materials SiO 2, GeSe 2, SiO 2-Na 2O,… Consider a system with n components having N1, N 2, …Nn particles. We can write % % $$ () = ( − − ) $ with α between [1,n] And for : !"# % ' $& () = ( − − ) $& Out of which can be computed the pair correlation function: 1 (can be also neutron or XRD weighted) = (( () ,( [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING Pair distribution function in multicomponent systems: GeO 2 Evidence for neighbour correlations Ge 3 Ge 2 Ge 1 O3 O1 O3 Ge 1 O2 O3 O1 O3 D. Marrocchelli et al., 2010 O1 O2 [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING Pair distribution function in multicomponent systems: GeSe 2 Evidence for homopolar bonds Ge-Ge and Se-Se Prepeaks in relevant pdfs [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING Thermodynamic quantities from the computed g(r): Energy First, one needs to remember that the energy is related to the partition function β as: Q(N,,, ) 7 where : / 1 4&5(6) - ., #, = 1 = 1 3 0 2 0 2 λ comes from the integration of the momentum p in the phase space given by: so that: [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING and In order to compute the average energy, one needs to compute the average potential U. Assume the case of a pairwise potential, so that: i.e. U is a sum of terms depending only between 2 particles, and thus contains N(N-1) terms. Then, we can write: (i.e. all terms in the first line are the exact same integrals, just with different labels) [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING ρ(2) which contains a two-body probability distribution function (r 1,r 2) so that <U> can be rewritten as : where we remind (slide 2) that : One thus arrives to the result: [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING Example : Glass transition in a model A-B glass Flores-Ruiz et al. PRB 2010 Reproduction of the glass transition phenomenon [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING Thermodynamic quantities from the computed g(r): Pressure We use the Maxwell relation: The volume dependence can be made explicit by changing the variables: so that we have from the partition function ZN the desired derivative from V: And: which involves the force Fi acting on a particle i [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING Again, for, pairwise interactions, Fi can be written as : and since one has (interchanging i-j summations): Using Newton’s third law, we furthermore have : and the Ensemble average is given by: [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING We do the same as for the energy: and for a pair potential Upair : And finally: The pressure can be computed from the derivative of the pair potential and from g(r). [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING Examples: equation of state of liquids SiO 2 GeO 2 Shell et al. PRE 2002 Micoulaut et al. PRE 2006 [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING B) STATIC STRUCTURE FACTOR For a simple liquid, the static structure factor is given by : ρ ρ where k is the Fourier transform of the microscopic density (r). This reads as: ‘ and, remembering that ρ one has: If isotropic and uniform medium, remember that ρ(r,r’)= ρ2g( r,r’) [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING Also, g( r,r’) depends only on | r-r’ |, i.e.: Or (isotropic fluid, everything depends only on k=| k|): The calculation of the structure factor S(k) is achieved via a Fourier transform of the pair distribution function g(r). [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING Calculating a structure factor S(k) from a MD simulation : 2 options 1. Calculate the pair correlation function g(r) from the MD trajectory, then use : 2. Calculate directly S(k) from the trajectory using: As 2Se 3 Differences between both methods can arise, and one is limited to r<L/2, i.e. k< πππ/L Effects of the components of the wavevector [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING Direct comparison with experiments : neutron or X-ray diffraction Intensity scattered in the direction kf Kob et al. 1999 Equal to the computed structur efactor. [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING Structure factor in multicomponent systems SiO 2, GeSe 2, SiO 2-Na 2O,… Consider a system with n components having N1, N 2, …Nn particles. We can write Faber-Ziman partial structure factors: % % (1 + $& ) =$& (>) = eApCD−E. − G 2 out of which can be computed a total structure factor: Neutron weighted : I,( JJ(KK(=( (H) = H = I,( JJ(KK( with the neutron scattering cross section , the concentration of the species bi ci =5.68 fm for Te (tabulated, depends on the isotope) bi X-ray weighted: I,( JJ(L(H)L((H)=( (H) = H = I,( JJ(L(H)L(( H) With the X-ray form factor (elastic or inelastic XRD) fi(k) [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING l-GeSe 2 v-SiO 2 Micoulaut et al., PRB 2009 [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING Various levels of agreement between theory and experiments can be found 5 Ag25 4 3 Ag15 ) Q ( 2 S Ag5 1 0 0 2 4 6 8 10 Q (Å-1 ) Micoulaut et al. 2013 Data Petri, Salmon, 1991 [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING Detailed structural analysis from MD Neighbor distribution Remember = 4 First minimum of g(r) can be used to define the coordination number. But this is an average. • Details are provided from the statistical analysis of each atom. • Allows to characterize the nature of the neighborhood • Can be extended to partial CN ( = ( 4 [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING Examples-1 Amorphous Ge 1Sb 2Te 4 Raty et al. Solid State Sciences 2010 Information on local geometry - short and long bond distance around Ge Straightforward - CN Te >2 4 neighbours around Ge,Si [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING Examples-2: Statistics of neighbors with homopolar bonds Ga 11 Ge 11 Te 78 Voleska et al., PRB 2013 [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING Detailed structural analysis from MD Bond angle distributions Depending on the system, provides information about the local geometry 1173 K (tetrahedral, octahedral,…). SnSe 2 Directional bonding vs non-directional SiO -Na O 300 K 2 2 Cormack and Du, JNCS 2001 Micoulaut et al. PRB 2008 [email protected] Atomic modeling of glass – LECTURE5 MD CALCULATING Detailed structural analysis from MD Ring statistics: serve to characterize the intermediate range order • Remember the early work of Galeener (lecture 3 ) and the Raman characterization of rings • Simulated positions can serve to define nodes and links.
Load more

Recommended publications
  • 2D Potts Model Correlation Lengths
    KOMA Revised version May D Potts Mo del Correlation Lengths Numerical Evidence for = at o d t Wolfhard Janke and Stefan Kappler Institut f ur Physik Johannes GutenbergUniversitat Mainz Staudinger Weg Mainz Germany Abstract We have studied spinspin correlation functions in the ordered phase of the twodimensional q state Potts mo del with q and at the rstorder transition p oint Through extensive Monte t Carlo simulations we obtain strong numerical evidence that the cor relation length in the ordered phase agrees with the exactly known and recently numerically conrmed correlation length in the disordered phase As a byproduct we nd the energy moments o t t d in the ordered phase at in very go o d agreement with a recent large t q expansion PACS numbers q Hk Cn Ha hep-lat/9509056 16 Sep 1995 Introduction Firstorder phase transitions have b een the sub ject of increasing interest in recent years They play an imp ortant role in many elds of physics as is witnessed by such diverse phenomena as ordinary melting the quark decon nement transition or various stages in the evolution of the early universe Even though there exists already a vast literature on this sub ject many prop erties of rstorder phase transitions still remain to b e investigated in detail Examples are nitesize scaling FSS the shap e of energy or magnetization distributions partition function zeros etc which are all closely interrelated An imp ortant approach to attack these problems are computer simulations Here the available system sizes are necessarily
    [Show full text]
  • Full and Unbiased Solution of the Dyson-Schwinger Equation in the Functional Integro-Differential Representation
    PHYSICAL REVIEW B 98, 195104 (2018) Full and unbiased solution of the Dyson-Schwinger equation in the functional integro-differential representation Tobias Pfeffer and Lode Pollet Department of Physics, Arnold Sommerfeld Center for Theoretical Physics, University of Munich, Theresienstrasse 37, 80333 Munich, Germany (Received 17 March 2018; revised manuscript received 11 October 2018; published 2 November 2018) We provide a full and unbiased solution to the Dyson-Schwinger equation illustrated for φ4 theory in 2D. It is based on an exact treatment of the functional derivative ∂/∂G of the four-point vertex function with respect to the two-point correlation function G within the framework of the homotopy analysis method (HAM) and the Monte Carlo sampling of rooted tree diagrams. The resulting series solution in deformations can be considered as an asymptotic series around G = 0 in a HAM control parameter c0G, or even a convergent one up to the phase transition point if shifts in G can be performed (such as by summing up all ladder diagrams). These considerations are equally applicable to fermionic quantum field theories and offer a fresh approach to solving functional integro-differential equations beyond any truncation scheme. DOI: 10.1103/PhysRevB.98.195104 I. INTRODUCTION was not solved and differences with the full, exact answer could be seen when the correlation length increases. Despite decades of research there continues to be a need In this work, we solve the full DSE by writing them as a for developing novel methods for strongly correlated systems. closed set of integro-differential equations. Within the HAM The standard Monte Carlo approaches [1–5] are convergent theory there exists a semianalytic way to treat the functional but suffer from a prohibitive sign problem, scaling exponen- derivatives without resorting to an infinite expansion of the tially in the system volume [6].
    [Show full text]
  • Notes on Statistical Field Theory
    Lecture Notes on Statistical Field Theory Kevin Zhou [email protected] These notes cover statistical field theory and the renormalization group. The primary sources were: • Kardar, Statistical Physics of Fields. A concise and logically tight presentation of the subject, with good problems. Possibly a bit too terse unless paired with the 8.334 video lectures. • David Tong's Statistical Field Theory lecture notes. A readable, easygoing introduction covering the core material of Kardar's book, written to seamlessly pair with a standard course in quantum field theory. • Goldenfeld, Lectures on Phase Transitions and the Renormalization Group. Covers similar material to Kardar's book with a conversational tone, focusing on the conceptual basis for phase transitions and motivation for the renormalization group. The notes are structured around the MIT course based on Kardar's textbook, and were revised to include material from Part III Statistical Field Theory as lectured in 2017. Sections containing this additional material are marked with stars. The most recent version is here; please report any errors found to [email protected]. 2 Contents Contents 1 Introduction 3 1.1 Phonons...........................................3 1.2 Phase Transitions......................................6 1.3 Critical Behavior......................................8 2 Landau Theory 12 2.1 Landau{Ginzburg Hamiltonian.............................. 12 2.2 Mean Field Theory..................................... 13 2.3 Symmetry Breaking.................................... 16 3 Fluctuations 19 3.1 Scattering and Fluctuations................................ 19 3.2 Position Space Fluctuations................................ 20 3.3 Saddle Point Fluctuations................................. 23 3.4 ∗ Path Integral Methods.................................. 24 4 The Scaling Hypothesis 29 4.1 The Homogeneity Assumption............................... 29 4.2 Correlation Lengths.................................... 30 4.3 Renormalization Group (Conceptual)..........................
    [Show full text]
  • 10 Basic Aspects of CFT
    10 Basic aspects of CFT An important break-through occurred in 1984 when Belavin, Polyakov and Zamolodchikov [BPZ84] applied ideas of conformal invariance to classify the possible types of critical behaviour in two dimensions. These ideas had emerged earlier in string theory and mathematics, and in fact go backto earlier (1970) work of Polyakov [Po70] in which global conformal invariance is used to constrain the form of correlation functions in d-dimensional the- ories. It is however only by imposing local conformal invariance in d =2 that this approach becomes really powerful. In particular, it immediately permitted a full classification of an infinite family of conformally invariant theories (the so-called “minimal models”) having a finite number of funda- mental (“primary”) fields, and the exact computation of the corresponding critical exponents. In the aftermath of these developments, conformal field theory (CFT) became for some years one of the most hectic research fields of theoretical physics, and indeed has remained a very active area up to this date. This chapter focusses on the basic aspects of CFT, with a special emphasis on the ingredients which will allow us to tackle the geometrically defined loop models via the so-called Coulomb Gas (CG) approach. The CG technique will be exposed in the following chapter. The aim is to make the presentation self- contained while remaining rather brief; the reader interested in more details should turn to the comprehensive textbook [DMS87] or the Les Houches volume [LH89]. 10.1 Global conformal invariance A conformal transformation in d dimensions is an invertible mapping x x′ → which multiplies the metric tensor gµν (x) by a space-dependent scale factor: gµ′ ν (x′)=Λ(x)gµν (x).
    [Show full text]
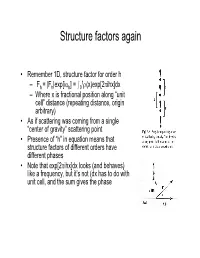
  • Structure Factors Again
    Structure factors again • Remember 1D, structure factor for order h 1 –Fh = |Fh|exp[iαh] = I0 ρ(x)exp[2πihx]dx – Where x is fractional position along “unit cell” distance (repeating distance, origin arbitrary) • As if scattering was coming from a single “center of gravity” scattering point • Presence of “h” in equation means that structure factors of different orders have different phases • Note that exp[2πihx]dx looks (and behaves) like a frequency, but it’s not (dx has to do with unit cell, and the sum gives the phase Back and Forth • Fourier sez – For any function f(x), there is a “transform” of it which is –F(h) = Ûf(x)exp(2pi(hx))dx – Where h is reciprocal of x (1/x) – Structure factors look like that • And it works backward –f(x) = ÛF(h)exp(-2pi(hx))dh – Or, if h comes only in discrete points –f(x) = SF(h)exp(-2pi(hx)) Structure factors, cont'd • Structure factors are a "Fourier transform" - a sum of components • Fourier transforms are reversible – From summing distribution of ρ(x), get hth order of diffraction – From summing hth orders of diffraction, get back ρ(x) = Σ Fh exp[-2πihx] Two dimensional scattering • In Frauenhofer diffraction (1D), we considered scattering from points, along the line • In 2D diffraction, scattering would occur from lines. • Numbering of the lines by where they cut the edges of a unit cell • Atom density in various lines can differ • Reflections now from planes Extension to 3D – Planes defined by extension from 2D case – Unit cells differ • Depends on arrangement of materials in 3D lattice • = "Space
    [Show full text]
  • System Design and Verification of the Precession Electron Diffraction Technique
    NORTHWESTERN UNIVERSITY System Design and Verification of the Precession Electron Diffraction Technique A DISSERTATION SUBMITTED TO THE GRADUATE SCHOOL IN PARTIAL FULFILLMENT OF THE REQUIREMENTS for the degree DOCTOR OF PHILOSOPHY Field of Materials Science and Engineering By Christopher Su-Yan Own EVANSTON, ILLINOIS First published on the WWW 01, August 2005 Build 05.12.07. PDF available for download at: http://www.numis.northwestern.edu/Research/Current/precession.shtml c Copyright by Christopher Su-Yan Own 2005 All Rights Reserved ii ABSTRACT System Design and Verification of the Precession Electron Diffraction Technique Christopher Su-Yan Own Bulk structural crystallography is generally a two-part process wherein a rough starting structure model is first derived, then later refined to give an accurate model of the structure. The critical step is the deter- mination of the initial model. As materials problems decrease in length scale, the electron microscope has proven to be a versatile and effective tool for studying many problems. However, study of complex bulk structures by electron diffraction has been hindered by the problem of dynamical diffraction. This phenomenon makes bulk electron diffraction very sensitive to specimen thickness, and expensive equip- ment such as aberration-corrected scanning transmission microscopes or elaborate methodology such as high resolution imaging combined with diffraction and simulation are often required to generate good starting structures. The precession electron diffraction technique (PED), which has the ability to significantly reduce dynamical effects in diffraction patterns, has shown promise as being a “philosopher’s stone” for bulk electron diffraction. However, a comprehensive understanding of its abilities and limitations is necessary before it can be put into widespread use as a standalone technique.
    [Show full text]
  • Form and Structure Factors: Modeling and Interactions Jan Skov Pedersen, Department of Chemistry and Inano Center University of Aarhus Denmark SAXS Lab
    Form and Structure Factors: Modeling and Interactions Jan Skov Pedersen, Department of Chemistry and iNANO Center University of Aarhus Denmark SAXS lab 1 Outline • Model fitting and least-squares methods • Available form factors ex: sphere, ellipsoid, cylinder, spherical subunits… ex: polymer chain • Monte Carlo integration for form factors of complex structures • Monte Carlo simulations for form factors of polymer models • Concentration effects and structure factors Zimm approach Spherical particles Elongated particles (approximations) Polymers 2 Motivation - not to replace shape reconstruction and crystal-structure based modeling – we use the methods extensively - alternative approaches to reduce the number of degrees of freedom in SAS data structural analysis (might make you aware of the limited information content of your data !!!) - provide polymer-theory based modeling of flexible chains - describe and correct for concentration effects 3 Literature Jan Skov Pedersen, Analysis of Small-Angle Scattering Data from Colloids and Polymer Solutions: Modeling and Least-squares Fitting (1997). Adv. Colloid Interface Sci. , 70 , 171-210. Jan Skov Pedersen Monte Carlo Simulation Techniques Applied in the Analysis of Small-Angle Scattering Data from Colloids and Polymer Systems in Neutrons, X-Rays and Light P. Lindner and Th. Zemb (Editors) 2002 Elsevier Science B.V. p. 381 Jan Skov Pedersen Modelling of Small-Angle Scattering Data from Colloids and Polymer Systems in Neutrons, X-Rays and Light P. Lindner and Th. Zemb (Editors) 2002 Elsevier
    [Show full text]
  • Introduction to Two-Dimensional Conformal Field Theory
    Introduction to two-dimensional conformal field theory Sylvain Ribault CEA Saclay, Institut de Physique Th´eorique [email protected] February 5, 2019 Abstract We introduce conformal field theory in two dimensions, from the basic principles to some of the simplest models. From the representations of the Virasoro algebra on the one hand, and the state-field correspondence on the other hand, we deduce Ward identities and Belavin{Polyakov{Zamolodchikov equations for correlation functions. We then explain the principles of the conformal bootstrap method, and introduce conformal blocks. This allows us to define and solve minimal models and Liouville theory. We also introduce the free boson with its abelian affine Lie algebra. Lecture notes for the \Young Researchers Integrability School", Wien 2019, based on the earlier lecture notes [1]. Estimated length: 7 lectures of 45 minutes each. Material that may be skipped in the lectures is in green boxes. Exercises are in green boxes when their statements are not part of the lectures' text; this does not make them less interesting as exercises. 1 Contents 0 Introduction2 1 The Virasoro algebra and its representations3 1.1 Algebra.....................................3 1.2 Representations.................................4 1.3 Null vectors and degenerate representations.................5 2 Conformal field theory6 2.1 Fields......................................6 2.2 Correlation functions and Ward identities...................8 2.3 Belavin{Polyakov{Zamolodchikov equations................. 10 2.4 Free boson.................................... 10 3 Conformal bootstrap 12 3.1 Single-valuedness................................ 12 3.2 Operator product expansion and crossing symmetry............. 13 3.3 Degenerate fields and the fusion product................... 16 4 Minimal models 17 4.1 Diagonal minimal models...........................
    [Show full text]
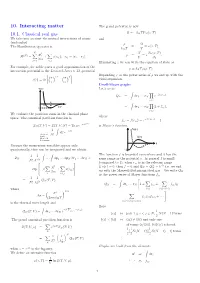
  • 10. Interacting Matter 10.1. Classical Real
    10. Interacting matter The grand potential is now Ω= k TVω(z,T ) 10.1. Classical real gas − B We take into account the mutual interactions of atoms and (molecules) p Ω The Hamiltonian operator is = = ω(z,T ) kBT −V N p2 N ∂ω(z,T ) H(N) = i + v(r ), r = r r . ρ = = z . 2m ij ij | i − j | V ∂z i=1 i<j X X Eliminating z we can write the equation of state as For example, for noble gases a good approximation of the p = k T ϕ(ρ,T ). interaction potential is the Lennard-Jones 6–12 -potential B Expanding ϕ as the power series of ρ we end up with the σ 12 σ 6 v(r)=4ǫ . virial expansion. r − r Ursell-Mayer graphs V ( r ) Let’s write Q = dr r e−βv(rij ) N 1 · · · N i<j Z Y r 0 s r 6 = dr r (1 + f ), e 1 / r 1 · · · N ij Z i<j We evaluate the partition sums in the classical phase Y where space. The canonical partition function is f = f(r )= e−βv(rij ) 1 ij ij − −βH(N) ZN (T, V )= Z(T,V,N) = Tr N e is Mayer’s function. 1 V ( r ) dΓ e−βH . classical−→ N! limit, Maxwell- Z f ( r ) Boltzman Because the momentum variables appear only r quadratically, they can be integrated and we obtain - 1 1 1 The function f is bounded everywhere and it has the ZN = dp1 dpN dr1 drN same range as the potential v.
    [Show full text]
  • Direct Phase Determination in Protein Electron Crystallography
    Proc. Natl. Acad. Sci. USA Vol. 94, pp. 1791–1794, March 1997 Biophysics Direct phase determination in protein electron crystallography: The pseudo-atom approximation (electron diffractionycrystal structure analysisydirect methodsymembrane proteins) DOUGLAS L. DORSET Electron Diffraction Department, Hauptman–Woodward Medical Research Institute, Inc., 73 High Street, Buffalo, NY 14203-1196 Communicated by Herbert A. Hauptman, Hauptman–Woodward Medical Research Institute, Buffalo, NY, December 12, 1996 (received for review October 28, 1996) ABSTRACT The crystal structure of halorhodopsin is Another approach to such phasing problems, especially in determined directly in its centrosymmetric projection using cases where the structures have appropriate distributions of 6.0-Å-resolution electron diffraction intensities, without in- mass, would be to adopt a pseudo-atom approach. The concept cluding any previous phase information from the Fourier of using globular sub-units as quasi-atoms was discussed by transform of electron micrographs. The potential distribution David Harker in 1953, when he showed that an appropriate in the projection is assumed a priori to be an assembly of globular scattering factor could be used to normalize the globular densities. By an appropriate dimensional re-scaling, low-resolution diffraction intensities with higher accuracy than these ‘‘globs’’ are then assumed to be pseudo-atoms for the actual atomic scattering factors employed for small mol- normalization of the observed structure factors. After this ecule structures
    [Show full text]
  • Solid State Physics: Problem Set #3 Structural Determination Via X-Ray Scattering Due: Friday Jan
    Physics 375 Fall (12) 2003 Solid State Physics: Problem Set #3 Structural Determination via X-Ray Scattering Due: Friday Jan. 31 by 6 pm Reading assignment: for Monday, 3.2-3.3 (structure factors for different lattices) for Wednesday, 3.4-3.7 (scattering methods) for Friday, 4.1-4.3 (mechanical properties of crystals) Problem assignment: Chapter 3 Problems: *3.1 Debye-Scherrer analysis (identify the crystal structure) [Robert] 3.2 Lattice parameter from Debye-Scherrer data 3.11 Measuring thermal expansion with X-ray scattering A1. The unit cell dimension of fcc copper is 0.36 nm. Calculate the longest wavelength of X- rays which will produce diffraction from the close packed planes. From what planes could X- rays with l=0.50 nm be diffracted? *A2. Single crystal diffraction: A cubic crystal with lattice spacing 0.4 nm is mounted with its [001] axis perpendicular to an incident X-ray beam of wavelength 0.1 nm. Initially the crystal is set so as to produce a diffracted beam associated with the (020) planes. Calculate the angle through which the crystal must be turned in order to produce a beam from the (hkl) planes where: a) (hkl)=(030) b) (hkl)=(130) [Brian] c) Which of these diffracted beams would be forbidden if the crystal is: i) sc; ii) bcc; iii) fcc A3. Structure factors for the fcc and diamond bases. a) Construct the structure factor Shkl for the fcc lattice and show that it vanishes unless h, k, and l are all even or all odd. b) Construct the structure factor Shkl for the diamond lattice and show that it vanishes unless h, k, and l are all odd or h+k+l=4n where n is an integer.
    [Show full text]
  • Recursive Graphical Solution of Closed Schwinger-Dyson
    Recursive Graphical Solution of Closed Schwinger-Dyson Equations in φ4-Theory – Part1: Generation of Connected and One-Particle Irreducible Feynman Diagrams Axel Pelster and Konstantin Glaum Institut f¨ur Theoretische Physik, Freie Universit¨at Berlin, Arnimallee 14, 14195 Berlin, Germany [email protected],[email protected] (Dated: November 11, 2018) Using functional derivatives with respect to the free correlation function we derive a closed set of Schwinger-Dyson equations in φ4-theory. Its conversion to graphical recursion relations allows us to systematically generate all connected and one-particle irreducible Feynman diagrams for the two- and four-point function together with their weights. PACS numbers: 05.70.Fh,64.60.-i I. INTRODUCTION Quantum and statistical field theory investigate the influence of field fluctuations on the n-point functions. Interactions lead to an infinite hierarchy of Schwinger-Dyson equations for the n-point functions [1–6]. These integral equations can only be closed approximately, for instance, by the well-established the self-consistent method of Kadanoff and Baym [7]. Recently, it has been shown that the Schwinger-Dyson equations of QED can be closed in a certain functional- analytic sense [8]. Using functional derivatives with respect to the free propagators and the interaction [8–14] two closed sets of equations were derived. The first one involves the connected electron and two-point function as well as the connected three-point function, whereas the second one determines the electron and photon self-energy as well as the one-particle irreducible three-point function. Their conversion to graphical recursion relations leads to a systematic graphical generation of all connected and one-particle irreducible Feynman diagrams in QED, respectively.
    [Show full text]