Cross-Cultural Data Shows Musical Scales Evolved to Maximise Imperfect fifths
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Chords and Scales 30/09/18 3:21 PM
Chords and Scales 30/09/18 3:21 PM Chords Charts written by Mal Webb 2014-18 http://malwebb.com Name Symbol Alt. Symbol (best first) Notes Note numbers Scales (in order of fit). C major (triad) C Cmaj, CM (not good) C E G 1 3 5 Ion, Mix, Lyd, MajPent, MajBlu, DoHar, HarmMaj, RagPD, DomPent C 6 C6 C E G A 1 3 5 6 Ion, MajPent, MajBlu, Lyd, Mix C major 7 C∆ Cmaj7, CM7 (not good) C E G B 1 3 5 7 Ion, Lyd, DoHar, RagPD, MajPent C major 9 C∆9 Cmaj9 C E G B D 1 3 5 7 9 Ion, Lyd, MajPent C 7 (or dominant 7th) C7 CM7 (not good) C E G Bb 1 3 5 b7 Mix, LyDom, PhrDom, DomPent, RagCha, ComDim, MajPent, MajBlu, Blues C 9 C9 C E G Bb D 1 3 5 b7 9 Mix, LyDom, RagCha, DomPent, MajPent, MajBlu, Blues C 7 sharp 9 C7#9 C7+9, C7alt. C E G Bb D# 1 3 5 b7 #9 ComDim, Blues C 7 flat 9 C7b9 C7alt. C E G Bb Db 1 3 5 b7 b9 ComDim, PhrDom C 7 flat 5 C7b5 C E Gb Bb 1 3 b5 b7 Whole, LyDom, SupLoc, Blues C 7 sharp 11 C7#11 Bb+/C C E G Bb D F# 1 3 5 b7 9 #11 LyDom C 13 C 13 C9 add 13 C E G Bb D A 1 3 5 b7 9 13 Mix, LyDom, DomPent, MajBlu, Blues C minor (triad) Cm C-, Cmin C Eb G 1 b3 5 Dor, Aeo, Phr, HarmMin, MelMin, DoHarMin, MinPent, Ukdom, Blues, Pelog C minor 7 Cm7 Cmin7, C-7 C Eb G Bb 1 b3 5 b7 Dor, Aeo, Phr, MinPent, UkDom, Blues C minor major 7 Cm∆ Cm maj7, C- maj7 C Eb G B 1 b3 5 7 HarmMin, MelMin, DoHarMin C minor 6 Cm6 C-6 C Eb G A 1 b3 5 6 Dor, MelMin C minor 9 Cm9 C-9 C Eb G Bb D 1 b3 5 b7 9 Dor, Aeo, MinPent C diminished (triad) Cº Cdim C Eb Gb 1 b3 b5 Loc, Dim, ComDim, SupLoc C diminished 7 Cº7 Cdim7 C Eb Gb A(Bbb) 1 b3 b5 6(bb7) Dim C half diminished Cø -

The 17-Tone Puzzle — and the Neo-Medieval Key That Unlocks It
The 17-tone Puzzle — And the Neo-medieval Key That Unlocks It by George Secor A Grave Misunderstanding The 17 division of the octave has to be one of the most misunderstood alternative tuning systems available to the microtonal experimenter. In comparison with divisions such as 19, 22, and 31, it has two major advantages: not only are its fifths better in tune, but it is also more manageable, considering its very reasonable number of tones per octave. A third advantage becomes apparent immediately upon hearing diatonic melodies played in it, one note at a time: 17 is wonderful for melody, outshining both the twelve-tone equal temperament (12-ET) and the Pythagorean tuning in this respect. The most serious problem becomes apparent when we discover that diatonic harmony in this system sounds highly dissonant, considerably more so than is the case with either 12-ET or the Pythagorean tuning, on which we were hoping to improve. Without any further thought, most experimenters thus consign the 17-tone system to the discard pile, confident in the knowledge that there are, after all, much better alternatives available. My own thinking about 17 started in exactly this way. In 1976, having been a microtonal experimenter for thirteen years, I went on record, dismissing 17-ET in only a couple of sentences: The 17-tone equal temperament is of questionable harmonic utility. If you try it, I doubt you’ll stay with it for long.1 Since that time I have become aware of some things which have caused me to change my opinion completely. -

Kūnqǔ in Practice: a Case Study
KŪNQǓ IN PRACTICE: A CASE STUDY A DISSERTATION SUBMITTED TO THE GRADUATE DIVISION OF THE UNIVERSITY OF HAWAI‘I AT MĀNOA IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY IN THEATRE OCTOBER 2019 By Ju-Hua Wei Dissertation Committee: Elizabeth A. Wichmann-Walczak, Chairperson Lurana Donnels O’Malley Kirstin A. Pauka Cathryn H. Clayton Shana J. Brown Keywords: kunqu, kunju, opera, performance, text, music, creation, practice, Wei Liangfu © 2019, Ju-Hua Wei ii ACKNOWLEDGEMENTS I wish to express my gratitude to the individuals who helped me in completion of my dissertation and on my journey of exploring the world of theatre and music: Shén Fúqìng 沈福庆 (1933-2013), for being a thoughtful teacher and a father figure. He taught me the spirit of jīngjù and demonstrated the ultimate fine art of jīngjù music and singing. He was an inspiration to all of us who learned from him. And to his spouse, Zhāng Qìnglán 张庆兰, for her motherly love during my jīngjù research in Nánjīng 南京. Sūn Jiàn’ān 孙建安, for being a great mentor to me, bringing me along on all occasions, introducing me to the production team which initiated the project for my dissertation, attending the kūnqǔ performances in which he was involved, meeting his kūnqǔ expert friends, listening to his music lessons, and more; anything which he thought might benefit my understanding of all aspects of kūnqǔ. I am grateful for all his support and his profound knowledge of kūnqǔ music composition. Wichmann-Walczak, Elizabeth, for her years of endeavor producing jīngjù productions in the US. -

3 Manual Microtonal Organ Ruben Sverre Gjertsen 2013
3 Manual Microtonal Organ http://www.bek.no/~ruben/Research/Downloads/software.html Ruben Sverre Gjertsen 2013 An interface to existing software A motivation for creating this instrument has been an interest for gaining experience with a large range of intonation systems. This software instrument is built with Max 61, as an interface to the Fluidsynth object2. Fluidsynth offers possibilities for retuning soundfont banks (Sf2 format) to 12-tone or full-register tunings. Max 6 introduced the dictionary format, which has been useful for creating a tuning database in text format, as well as storing presets. This tuning database can naturally be expanded by users, if tunings are written in the syntax read by this instrument. The freely available Jeux organ soundfont3 has been used as a default soundfont, while any instrument in the sf2 format can be loaded. The organ interface The organ window 3 MIDI Keyboards This instrument contains 3 separate fluidsynth modules, named Manual 1-3. 3 keysliders can be played staccato by the mouse for testing, while the most musically sufficient option is performing from connected MIDI keyboards. Available inputs will be automatically recognized and can be selected from the menus. To keep some of the manuals silent, select the bottom alternative "to 2ManualMicroORGANircamSpat 1", which will not receive MIDI signal, unless another program (for instance Sibelius) is sending them. A separate menu can be used to select a foot trigger. The red toggle must be pressed for this to be active. This has been tested with Behringer FCB1010 triggers. Other devices could possibly require adjustments to the patch. -

Electrophonic Musical Instruments
G10H CPC COOPERATIVE PATENT CLASSIFICATION G PHYSICS (NOTES omitted) INSTRUMENTS G10 MUSICAL INSTRUMENTS; ACOUSTICS (NOTES omitted) G10H ELECTROPHONIC MUSICAL INSTRUMENTS (electronic circuits in general H03) NOTE This subclass covers musical instruments in which individual notes are constituted as electric oscillations under the control of a performer and the oscillations are converted to sound-vibrations by a loud-speaker or equivalent instrument. WARNING In this subclass non-limiting references (in the sense of paragraph 39 of the Guide to the IPC) may still be displayed in the scheme. 1/00 Details of electrophonic musical instruments 1/053 . during execution only {(voice controlled (keyboards applicable also to other musical instruments G10H 5/005)} instruments G10B, G10C; arrangements for producing 1/0535 . {by switches incorporating a mechanical a reverberation or echo sound G10K 15/08) vibrator, the envelope of the mechanical 1/0008 . {Associated control or indicating means (teaching vibration being used as modulating signal} of music per se G09B 15/00)} 1/055 . by switches with variable impedance 1/0016 . {Means for indicating which keys, frets or strings elements are to be actuated, e.g. using lights or leds} 1/0551 . {using variable capacitors} 1/0025 . {Automatic or semi-automatic music 1/0553 . {using optical or light-responsive means} composition, e.g. producing random music, 1/0555 . {using magnetic or electromagnetic applying rules from music theory or modifying a means} musical piece (automatically producing a series of 1/0556 . {using piezo-electric means} tones G10H 1/26)} 1/0558 . {using variable resistors} 1/0033 . {Recording/reproducing or transmission of 1/057 . by envelope-forming circuits music for electrophonic musical instruments (of 1/0575 . -

Construction and Verification of the Scale Detection Method for Traditional Japanese Music – a Method Based on Pitch Sequence of Musical Scales –
International Journal of Affective Engineering Vol.12 No.2 pp.309-315 (2013) Special Issue on KEER 2012 ORIGINAL ARTICLE Construction and Verification of the Scale Detection Method for Traditional Japanese Music – A Method Based on Pitch Sequence of Musical Scales – Akihiro KAWASE Department of Corpus Studies, National Institute for Japanese Language and Linguistics, 10-2 Midori-cho, Tachikawa City, Tokyo 190-8561, Japan Abstract: In this study, we propose a method for automatically detecting musical scales from Japanese musical pieces. A scale is a series of musical notes in ascending or descending order, which is an important element for describing the tonal system (Tonesystem) and capturing the characteristics of the music. The study of scale theory has a long history. Many scale theories for Japanese music have been designed up until this point. Out of these, we chose to formulate a scale detection method based on Seiichi Tokawa’s scale theories for traditional Japanese music, because Tokawa’s scale theories provide a versatile system that covers various conventional scale theories. Since Tokawa did not describe any of his scale detection procedures in detail, we started by analyzing his theories and understanding their characteristics. Based on the findings, we constructed the scale detection method and implemented it in the Java Runtime Environment. Specifically, we sampled 1,794 works from the Nihon Min-yo Taikan (Anthology of Japanese Folk Songs, 1944-1993), and performed the method. We compared the detection results with traditional research results in order to verify the detection method. If the various scales of Japanese music can be automatically detected, it will facilitate the work of specifying scales, which promotes the humanities analysis of Japanese music. -

Convergent Evolution in a Large Cross-Cultural Database of Musical Scales
Convergent evolution in a large cross-cultural database of musical scales John M. McBride1,* and Tsvi Tlusty1,2,* 1Center for Soft and Living Matter, Institute for Basic Science, Ulsan 44919, South Korea 2Departments of Physics and Chemistry, Ulsan National Institute of Science and Technology, Ulsan 44919, South Korea *[email protected], [email protected] August 3, 2021 Abstract We begin by clarifying some key terms and ideas. We first define a scale as a sequence of notes (Figure 1A). Scales, sets of discrete pitches used to generate Notes are pitch categories described by a single pitch, melodies, are thought to be one of the most uni- although in practice pitch is variable so a better descrip- versal features of music. Despite this, we know tion is that notes are regions of semi-stable pitch centered relatively little about how cross-cultural diversity, around a representative (e.g., mean, meadian) frequency or how scales have evolved. We remedy this, in [10]. Thus, a scale can also be thought of as a sequence of part, we assemble a cross-cultural database of em- mean frequencies of pitch categories. However, humans pirical scale data, collected over the past century process relative frequency much better than absolute fre- by various ethnomusicologists. We provide sta- quency, such that a scale is better described by the fre- tistical analyses to highlight that certain intervals quency of notes relative to some standard; this is typically (e.g., the octave) are used frequently across cul- taken to be the first note of the scale, which is called the tures. -

Major and Minor Scales Half and Whole Steps
Dr. Barbara Murphy University of Tennessee School of Music MAJOR AND MINOR SCALES HALF AND WHOLE STEPS: half-step - two keys (and therefore notes/pitches) that are adjacent on the piano keyboard whole-step - two keys (and therefore notes/pitches) that have another key in between chromatic half-step -- a half step written as two of the same note with different accidentals (e.g., F-F#) diatonic half-step -- a half step that uses two different note names (e.g., F#-G) chromatic half step diatonic half step SCALES: A scale is a stepwise arrangement of notes/pitches contained within an octave. Major and minor scales contain seven notes or scale degrees. A scale degree is designated by an Arabic numeral with a cap (^) which indicate the position of the note within the scale. Each scale degree has a name and solfege syllable: SCALE DEGREE NAME SOLFEGE 1 tonic do 2 supertonic re 3 mediant mi 4 subdominant fa 5 dominant sol 6 submediant la 7 leading tone ti MAJOR SCALES: A major scale is a scale that has half steps (H) between scale degrees 3-4 and 7-8 and whole steps between all other pairs of notes. 1 2 3 4 5 6 7 8 W W H W W W H TETRACHORDS: A tetrachord is a group of four notes in a scale. There are two tetrachords in the major scale, each with the same order half- and whole-steps (W-W-H). Therefore, a tetrachord consisting of W-W-H can be the top tetrachord or the bottom tetrachord of a major scale. -

Helmholtz's Dissonance Curve
Tuning and Timbre: A Perceptual Synthesis Bill Sethares IDEA: Exploit psychoacoustic studies on the perception of consonance and dissonance. The talk begins by showing how to build a device that can measure the “sensory” consonance and/or dissonance of a sound in its musical context. Such a “dissonance meter” has implications in music theory, in synthesizer design, in the con- struction of musical scales and tunings, and in the design of musical instruments. ...the legacy of Helmholtz continues... 1 Some Observations. Why do we tune our instruments the way we do? Some tunings are easier to play in than others. Some timbres work well in certain scales, but not in others. What makes a sound easy in 19-tet but hard in 10-tet? “The timbre of an instrument strongly affects what tuning and scale sound best on that instrument.” – W. Carlos 2 What are Tuning and Timbre? 196 384 589 amplitude 787 magnitude sample: 0 10000 20000 30000 0 1000 2000 3000 4000 time: 0 0.23 0.45 0.68 frequency in Hz Tuning = pitch of the fundamental (in this case 196 Hz) Timbre involves (a) pattern of overtones (Helmholtz) (b) temporal features 3 Some intervals “harmonious” and others “discordant.” Why? X X X X 1.06:1 2:1 X X X X 1.89:1 3:2 X X X X 1.414:1 4:3 4 Theory #1:(Pythagoras ) Humans naturally like the sound of intervals de- fined by small integer ratios. small ratios imply short period of repetition short = simple = sweet Theory #2:(Helmholtz ) Partials of a sound that are close in frequency cause beats that are perceived as “roughness” or dissonance. -

When the Leading Tone Doesn't Lead: Musical Qualia in Context
When the Leading Tone Doesn't Lead: Musical Qualia in Context Dissertation Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Claire Arthur, B.Mus., M.A. Graduate Program in Music The Ohio State University 2016 Dissertation Committee: David Huron, Advisor David Clampitt Anna Gawboy c Copyright by Claire Arthur 2016 Abstract An empirical investigation is made of musical qualia in context. Specifically, scale-degree qualia are evaluated in relation to a local harmonic context, and rhythm qualia are evaluated in relation to a metrical context. After reviewing some of the philosophical background on qualia, and briefly reviewing some theories of musical qualia, three studies are presented. The first builds on Huron's (2006) theory of statistical or implicit learning and melodic probability as significant contributors to musical qualia. Prior statistical models of melodic expectation have focused on the distribution of pitches in melodies, or on their first-order likelihoods as predictors of melodic continuation. Since most Western music is non-monophonic, this first study investigates whether melodic probabilities are altered when the underlying harmonic accompaniment is taken into consideration. This project was carried out by building and analyzing a corpus of classical music containing harmonic analyses. Analysis of the data found that harmony was a significant predictor of scale-degree continuation. In addition, two experiments were carried out to test the perceptual effects of context on musical qualia. In the first experiment participants rated the perceived qualia of individual scale-degrees following various common four-chord progressions that each ended with a different harmony. -

HOW to FIND RELATIVE MINOR and MAJOR SCALES Relative
HOW TO FIND RELATIVE MINOR AND MAJOR SCALES Relative minor and major scales share all the same notes–each one just has a different tonic. The best example of this is the relative relationship between C-major and A-minor. These two scales have a relative relationship and therefore share all the same notes. C-major: C D E F G A B C A-minor: A B C D E F G A Finding the relative minor from a known major scale (using the 6th scale degree) scale degrees: 1 2 3 4 5 6 7 1 C-major: C D E F G A B C A-(natural) minor: A B C D E F G A A-minor starts on the 6th scale degree of C-major. This relationship holds true for ALL major and minor scale relative relationships. To find the relative minor scale from a given major scale, count up six scale degrees in the major scale–that is where the relative minor scale begins. This minor scale will be the natural minor mode. 1 2 3 4 5 6 C-D-E-F-G-A The relative minor scale can also be found by counting backwards (down) by three scale degrees in the major scale. C-major: C D E F G A B C ←←← count DOWN three scale degrees and arrive at A 1 2 3 C-B-A Finding the relative major from a known minor scale (using the 3rd scale degree) scale degrees: 1 2 3 4 5 6 7 1 A-(natural) minor: A B C D E F G A C-major: C D E F G A B C C-major starts on the 3rd scale of A-minor. -

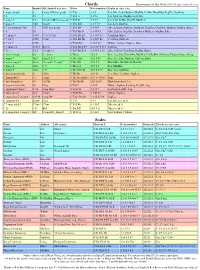
250 + Musical Scales and Scalecodings
250 + Musical Scales and Scalecodings Number Note Names Of Notes Ascending Name Of Scale In Scale from C ScaleCoding Major Suspended 4th Chord 4 C D F G 3/0/2 Major b7 Suspend 4th Chord 4 C F G Bb 3/0/3 Major Pentatonic 5 C D E G A 4/0/1 Ritusen Japan, Scottish Pentatonic 5 C D F G A 4/0/2 Egyptian \ Suspended Pentatonic 5 C D F G Bb 4/0/3 Blues Pentatonic Minor, Hard Japan 5 C Eb F G Bb 4/0/4 Major 7-b5 Chord \ Messiaen Truncated Mode 4 C Eb G Bb 4/3/4 Minor b7 Chord 4 C Eb G Bb 4/3/4 Major Chord 3 C E G 4/34/1 Eskimo Tetratonic 4 C D E G 4/4/1 Lydian Hexatonic 6 C D E G A B 5/0/1 Scottish Hexatonic 6 C D E F G A 5/0/2 Mixolydian Hexatonic 6 C D F G A Bb 5/0/3 Phrygian Hexatonic 6 C Eb F G Ab Bb 5/0/5 Ritsu 6 C Db Eb F Ab Bb 5/0/6 Minor Pentachord 5 C D Eb F G 5/2/4 Major 7 Chord 4 C E G B 5/24/1 Phrygian Tetrachord 4 C Db Eb F 5/24/6 Dorian Tetrachord 4 C D Eb F 5/25/4 Major Tetrachord 4 C D E F 5/35/2 Warao Tetratonic 4 C D Eb Bb 5/35/4 Oriental 5 C D F A Bb 5/4/3 Major Pentachord 5 C D E F G 5/5/2 Han-Kumo? 5 C D F G Ab 5/23/5 Lydian, Kalyan F to E ascending naturals 7 C D E F# G A B 6/0/1 Ionian, Major, Bilaval C to B asc.