Digital Stereotomy and Topological Transformations: Reasoning About Shape Building
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Les Boiseries De La Salle Du Conseil D'état
Les boiseries de la salle du Conseil d'État Autor(en): Roth-Lochner, Barbara Objekttyp: Article Zeitschrift: Genava : revue d'histoire de l'art et d'archéologie Band (Jahr): 28 (1980) PDF erstellt am: 11.10.2021 Persistenter Link: http://doi.org/10.5169/seals-728521 Nutzungsbedingungen Die ETH-Bibliothek ist Anbieterin der digitalisierten Zeitschriften. Sie besitzt keine Urheberrechte an den Inhalten der Zeitschriften. Die Rechte liegen in der Regel bei den Herausgebern. Die auf der Plattform e-periodica veröffentlichten Dokumente stehen für nicht-kommerzielle Zwecke in Lehre und Forschung sowie für die private Nutzung frei zur Verfügung. Einzelne Dateien oder Ausdrucke aus diesem Angebot können zusammen mit diesen Nutzungsbedingungen und den korrekten Herkunftsbezeichnungen weitergegeben werden. Das Veröffentlichen von Bildern in Print- und Online-Publikationen ist nur mit vorheriger Genehmigung der Rechteinhaber erlaubt. Die systematische Speicherung von Teilen des elektronischen Angebots auf anderen Servern bedarf ebenfalls des schriftlichen Einverständnisses der Rechteinhaber. Haftungsausschluss Alle Angaben erfolgen ohne Gewähr für Vollständigkeit oder Richtigkeit. Es wird keine Haftung übernommen für Schäden durch die Verwendung von Informationen aus diesem Online-Angebot oder durch das Fehlen von Informationen. Dies gilt auch für Inhalte Dritter, die über dieses Angebot zugänglich sind. Ein Dienst der ETH-Bibliothek ETH Zürich, Rämistrasse 101, 8092 Zürich, Schweiz, www.library.ethz.ch http://www.e-periodica.ch Les boiseries de la salle du Conseil d'Etat par Barbara Roth-Lochner Lorsque les travaux de rénovation de la la salle du Conseil. Ce texte m'a incité à entre- salle du Conseil d'Etat à la Tour Baudet sont prendre une recherche, dont je livre ici les entrepris en 1901, les ouvriers ont la surprise résultats. -

Stéreoplexie STEREOTOMIES NUMERIQUES Entre Tradition Et
Séminaire doctoral 2018-2019 Domaine : Matérialité Pensée et Culture constructives STEREOTOMIES NUMERIQUES entre tradition et innovation Organisation, conception : Antonella Mastrorilli Professeure Sciences et Techniques pour l’Architecture – HDR- 15 mai 2019 Responsable du domaine Matérialité - LACTH Chercheur invité : Maurizio Brocato 14h30-17h30 Professeur Sciences et Techniques pour l’Architecture – HDR - salle Jean Challet Directeur du Laboratoire Géométrie, Structure, Architecture (1er étage) (GSA) – ENSA Paris Malaquais Autre chercheur : Mohammad Mansouri Architecte, Maître de conférence associé ENSAP Lille, chercheur au GSA Doctorant LACTH : Emmanuel Breton (LACTH-EDSHS Lille3) Architecte, Maître de conférence associé à l’ENSA de Marseille Discutant : Gilles Maury, Maître de conférence ENSAP Lille, chercheur au LACTH, domaine Histoire Apparemment désuète, oubliée, la stéréotomie, n’est plus enseignée dans les écoles d’architecture ni d’ingénieurs, pourtant elle offre des outils et des méthodes intéressants pour la recherche autour de l’architecture contemporaine. Aujourd’hui, des nouvelles déclinaisons morphologiques, rendues possibles par le tournant numérique permettent de revoir le registre d’écriture des matériaux employés. Les interventions proposées dans cette séance visent surtout à développer certains aspects de ces questions en interrogeant l’expérimentation constructive et le prototypage numérique. Mots clés : Construction, expérimentation constructive, géométrie constructive, modélisation, morphogenèse, morphologie -
Walking Downstream
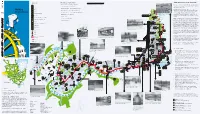
legende practical information 0 120 240 360 480 600 720 m technology and nature Scale 1:12 000 • "Plan piétons" Internet site www.ville-ge.ch/plan-pietons This newest course is a mix of technology and nature. Dams, Games bridges, pumping stations, baths, factories, tanks… water and • Commune of Vernier Internet site www.vernier.ch more water at man’s service. Commune Telephone de Vernier • Municipal information point 1, pont de la Machine, Tel. 311 99 70 We will go from the Pearl of the Lake to the Chèvres Walking Restroom • Mouettes Genevoises passenger ferry (reservation) Tel. 732 29 44 footbridge, strolling the length of the quay and following the anne Beverages banks of the Rhone for 15 miles along this “impetuous river” • Lake Geneva General Shipping Company (CGN) infoline: 0848 811 848 Mouettes Downstream (Celtic meaning of Rhone), which winds through the Genevoises Public Transportation (TPG) Jardin Botanique rte de Laus Baths of Pâquis around 1932 (SU) communes of Geneva and Vernier. For the return, why not • Public transportation (TPG) Tel. 308 34 34 7 Train station board one of the boats along the Rhone and take in its gentle • Taxi Tel. 33 141 33 18 stream? Lake Geneva General Shipping Co. (CGN) • Cornavin train station Tel. 157 22 22 Water is omnipresent along this walk. The very name Geneva Mouettes Genevoises passenger ferry comes from the Celtic words “gen,” mouth, and “ava,” water. • Weather conditions Tel. 162 av. de la Paix OMC OMM Car park The name Vernier also evokes water, deriving from “verne,” 4 meaning the alder, a tree particularly partial to river banks and r Sport, stadium, pool, paddleboats, tennis . -

Estudio Y Análisis De La Bóveda Plana De Joseph Abeille
ESTUDIO Y ANÁLISIS DE LA BÓVEDA PLANA DE JOSEPH ABEILLE TRABAJO DE FIN DE GRADO (CURSO 2019‐2020) AUTOR: Manuel Sánchez Peña TUTORA: María Dolores García Alonso AULA: 5 COORDINADORA: María Barbero Liñán Grado Universitario en Fundamentos de la Arquitectura Escuela Técnica Superior de Arquitectura de Madrid UPM A mi tutora María Dolores, por el esfuerzo y la energía volcadas en este trabajo, especialmente en estos meses tan difíciles de confinamiento. Sin ella no hubiese sido posible que este trabajo saliese adelante. Título Estudio y análisis de la bóveda plana de Joseph Abeille Autor Manuel Sánchez Peña Tutora María Dolores García Alonso Departamento Departamento de Estructuras y Física de la Edificación (DEFE) Aula TFG Aula 5 Coordinadora María Barbero Liñán Adjunta María de los Ángeles Navacerrada Saturio Fecha de entrega 8 de junio de 2020 Centro docente Escuela Técnica Superior de Arquitectura de Madrid (ETSAM) Universidad Politécnica de Madrid (UPM) http://etsamadrid.aq.upm.es/ «Creo que el material no necesita ser fuerte para construir una estructura fuerte. La fuerza de la estructura no tiene nada que ver con la fuerza del material.» Shigeru Ban ÍNDICE Objeto del trabajo y palabras clave ................................................................................ 1 Introducción ....................................................................................................................... 1 Motivación ..................................................................................................................... -

Book Chapter Reference
Book Chapter Aspects de l'architecture genevoise de la Réforme au XIXe siècle EL-WAKIL, Leïla Reference EL-WAKIL, Leïla. Aspects de l'architecture genevoise de la Réforme au XIXe siècle. In: Société genevoise des études italiennes. Genève et l'Italie. Genève : 1994. p. 177-199 Available at: http://archive-ouverte.unige.ch/unige:35359 Disclaimer: layout of this document may differ from the published version. 1 / 1 Aspects de l'architecture genevoise de la Réforme au XIXe siècle. La part de l'étranger entre répression et représentation Leïla el-Wakil Préambule Depuis la publication du Recueil de renseignements sur les beaux-arts à Genève (1845-1849), ouvrage précurseur du syndic esthète Jean-Jacques Rigaud, les histo riens ont trop souvent brossé de Genève le tableau d'une ville sans arts majeurs; ils ont généralement imputé la responsabilité de cet état de choses à Calvin et aux mesures prises contre le luxe. Tenassée lors des journées iconoclastes de 1535, l'activité artistique genevoise serait pendant longtemps restée en veilleuse. Brimée par de trop rigoureuses ordonnances somptuaires, elle aurait dû attendre la fin du XVIIIe siècle pour reprendre son essor. Entre temps elle se serait repliée dans les arts appliqués destinés à l'exportation, comme la bijouterie, l'orfévrerie, la peinture sur émail ou la gravure. Or s'il est indéniable que les retombées de la Réforme, et particulièrement la suppression de la commande religieuse, représentent un handicape majeur pour la production picturale et sculpturale1, elles n'ont en revanche que pen de conséquences sur la production aTchitecturale. Tout au contraire l'afflux d'étrangers venus se réfugier dans la Rome protestante imprime un élan bienvenu an bâtiment. -

Geological and Archeological Visit of Geneva
Geological and archeological Update July 3rd 2014 visit of Geneva Walter Wildi, Pierre Corboud, Stéphanie Girardclos, Georges Gorin Geological and archeological visit of Geneva Key words: geology, archeology, field trip, Geneva Walter Wildi, Pierre Corboud, Stéphanie Girardclos, Georges Gorin Christian [email protected] Section of Earth and Environmental Sciences Rue des Maraîchers 13, CH-1211 Genève 4 Copyright 2014 Document available on the website http://www.unige.ch/forel/Services/Visitegeologique_en.html 1 Table of contents Foreword ………………………………………………………………………………………………………………………………………………………………………........ 3 1.Introduction ……………………………………………………………………………………………………………………………………………………………………… 3 1.1. The natural site ……………...................................................................................................................................................... 3 1.2. Geological history of the Geneva Basin ………………………………………………………………………………………………………………………… 5 1.3. Human occupation of the Geneva site …………………………………………………………………………………………………………………………. 15 2. Site visit ……………………………………………………………………………………………………………………………………………………………………………. 24 Ge 1: Geological visit of Geneva City ……………………………………………………………………………………………………………………………….. 25 Ge 1.1: The Arve River: an Alpine river and its alluvial plain…………………………………………………………………………………………………. 27 Ge 1.2: Bois de la Bâtie: the «Alluvion ancienne», deposits of an old proglacial plain covered by the Upper Basal Moraine of the Rhône Glacier………………………………………………………………………………………………………………………………………………… 30 Ge 1.3: From the -

Le Château Comme Production Architecturale : Modèles, Artisans, Architectes – Essai De Synthèse Par Dave Lüthi
Le château comme production architecturale : modèles, artisans, architectes – Essai de synthèse par Dave Lüthi Le château du XVIIIe siècle, objet patrimonial mineur ? foyers artistiques à grand rayonnement et dans laquelle C’est ce que pourrait laisser penser l’absence de biblio- la circulation des artistes et des artisans défie souvent les graphie récente à son sujet en Suisse. Pour des raisons logiques historiques et confessionnelles. liées notamment au travail d’inventorisation, focalisé sur Grâce au dépouillement extensif d’archives privées et les villes, mais aussi à la rareté de la documentation his- au renouvellement des questions habituellement posées torique ainsi qu’à l’accès difficile de ces édifices souvent au château par les historiens de l’art, il est possible de en mains privées, cette importante part des monuments démontrer que ce monument n’est pas secondaire dans la helvétiques demeure très peu abordée ; elle l’est en géné- production artistique de l’Ancien Régime. Au contraire : ral de manière monographique et rarement transver- il doit être remis au centre des recherches, notamment sale,1 cantonnée à des frontières cantonales pas toujours dans les territoires réformés, où il représente souvent pertinentes historiquement.2 En outre, les a priori héri- une commande de premier plan, à l’instar des couvents tés de la littérature française sur le sujet ne stimulent dans les pays catholiques. Le corpus des édifices, faisant guère la recherche : situé en périphérie, le château serait référence au modèle français « entre cour et jardin » dans moins innovant et donc moins intéressant du point de les cantons protestants, permettra de resserrer le pro- vue de l’histoire de l’architecture que l’hôtel urbain, édi- fié lui dans les centres artistiques. -

Relecture De Quelques Cas Genevois
Article Cet homme nous fut envoyé par le ciel pour rénover l'architecture égarée depuis des siècles : relecture de quelques cas genevois EL-WAKIL, Leïla Reference EL-WAKIL, Leïla. Cet homme nous fut envoyé par le ciel pour rénover l'architecture égarée depuis des siècles : relecture de quelques cas genevois. La profession d'architecte en Suisse romande (XVIe - XXe siècle) Etudes de Lettres, 2009, vol. 1, p. 35-56 DOI : 10.4000/edl.523 Available at: http://archive-ouverte.unige.ch/unige:12788 Disclaimer: layout of this document may differ from the published version. 1 / 1 CET HOMME NOUS FUT ENVOYE PAR LE CIEL POUR RENOVER L 'ARCHITECTURE EGAREE DEPUIS DES SIECLES RELECTURE DE QUELQUES CAS GENEVOIS par Leïla el-WAKIL, PhD Département d’histoire de l’art UNIGE INTRODUCTION Relire l’histoire de l’architecture genevoise, comme celle de toute autre ville de province, à la lumière des apports internationaux, voilà le propos de cette courte contribution qui s’inscrit dans le cadre d’une réflexion sur le statut d’architecte en Suisse romande, statut dont, au demeurant même aujourd’hui, les contours ne toujours pas délimités avec discernement. Chacun sait que la profession d’architecte est parmi les professions libérales l’une de celles dont le titre est peu protégé ; nombreux sont ceux qui, du simple dessinateur en bâtiment au diplômé d’une haute école d’architecture, peuvent s’intituler architectes : « … la profession d’architecte, c’est à la fois une population dont la taille fluctue au fil du temps, une formation professionnelle qui diffère en fonction des cursus individuels accomplis à l’Université, à l’Ecole polytechnique, dans les écoles spécialisées ou en apprentissage « sur le tas » et, enfin, un statut qui varie au gré du fédéralisme à la sauce helvétique. -

Statut Architecte
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by RERO DOC Digital Library CET HOMME NOUS FUT ENVOYE PAR LE CIEL POUR RENOVER L 'ARCHITECTURE EGAREE DEPUIS DES SIECLES RELECTURE DE QUELQUES CAS GENEVOIS par Leïla el-WAKIL, PhD Département d’histoire de l’art UNIGE INTRODUCTION Relire l’histoire de l’architecture genevoise, comme celle de toute autre ville de province, à la lumière des apports internationaux, voilà le propos de cette courte contribution qui s’inscrit dans le cadre d’une réflexion sur le statut d’architecte en Suisse romande, statut dont, au demeurant même aujourd’hui, les contours ne toujours pas délimités avec discernement. Chacun sait que la profession d’architecte est parmi les professions libérales l’une de celles dont le titre est peu protégé ; nombreux sont ceux qui, du simple dessinateur en bâtiment au diplômé d’une haute école d’architecture, peuvent s’intituler architectes : « … la profession d’architecte, c’est à la fois une population dont la taille fluctue au fil du temps, une formation professionnelle qui diffère en fonction des cursus individuels accomplis à l’Université, à l’Ecole polytechnique, dans les écoles spécialisées ou en apprentissage « sur le tas » et, enfin, un statut qui varie au gré du fédéralisme à la sauce helvétique. »1 Dans certains cantons, la qualité d’architecte habilité à déposer des demandes en autorisation de construire n’est pas réellement définie, dans d’autres, elle est liée à l’inscription du mandataire au registre cantonal. A Genève l’architecte doit figurer au registre des mandataires professionnellement qualifiés reconnus par l’Etat ; cela implique généralement la possession d’un diplôme professionnel (Haute école ou école technique), d’une pratique de quelques années et d’une adresse professionnelle dans le canton 2. -

De L'architecte Voyer À L'ingenieur En Chef Des Services Techniques
UNIVERSITÉ PARIS I PANTHÉON-SORBONNE École doctorale 441 Histoire de l'art THÈSE POUR LE DOCTORAT D’HISTOIRE DE L’ART [HISTOIRE DE L’ARCHITECTURE] Gilles BIENVENU Laboratoire LAUA – école nationale supérieure d’architecture de Nantes Mars 2013 DE L’ARCHITECTE VOYER À L’INGENIEUR EN CHEF DES SERVICES TECHNIQUES LES SERVICES D’ARCHITECTURE ET D’URBANISME DE LA VILLE DE NANTES DU XVIIIe SIÈCLE AU XXe SIÈCLE ANNEXES Sous la direction de Monsieur Gérard MONNIER, professeur émérite à l’université Paris I Panthéon-Sorbonne Jury : MM. Robert CARVAIS, directeur de recherche au CNRS, université Paris II Panthéon-Assas, rapporteur Michaël DARIN, professeur à l’école nationale supérieure d’architecture de Strasbourg, rapporteur Daniel LE COUÉDIC, professeur à l’université de Bretagne occidentale DE L’ARCHITECTE-VOYER À L’INGÉNIEUR EN CHEF DES SERVICES TECHNIQUES LES SERVICES D’ARCHITECTURE ET D’URBANISME DE NANTES du XVIIIe siècle au XXe siècle ANNEXES Gilles Bienvenu Paris I Panthéon-Sorbonne ensa Nantes – LAUA mars 2013 Gilles Bienvenu notices biographiques 3 SOMMAIRE Notices biographiques sur les membres du personnel des services de la Ville de Nantes 5 Travaux et publications des architectes et ingénieurs communaux 35 Architectes membres du conseil municipal de Nantes 39 Architectes membres de la commission de révision du règlement de voirie en 1840 39 Composition du conseil départemental d’hygiène et de salubrité publique 39 selon arrêté du pouvoir exécutif du 18 décembre 1848 Tableau des Hommes de l’Art arrêté par le maire pour la visite mensuelle -

Producción Académica C I M : Centre D'innovation Multidisciplinaire a Rennes
UNIVERSIDAD CATÓLICA Sistema de Producción DE CÓRDOBA Bibliotecas JESUITAS Académica Vincenti, Nahuel C I M : Centre d'innovation multidisciplinaire a Rennes Tesis para la obtención del título de grado de Arquitecto Director: Santillán, José Ignacio Documento disponible para su consulta y descarga en Biblioteca Digital - Producción Académica, repositorio institucional de la Universidad Católica de Córdoba, gestionado por el Sistema de Bibliotecas de la UCC. Esta obra está bajo licencia 2.5 de Creative Commons Argentina. Atribución-No comercial-Sin obras derivadas 2.5 TRABAJO FINAL DE CARRERA UNIVERSIDAD CÁTOLICA DE CÓRDOBA FACULTAD DE ARQUITECTURA UNIVERSIDAD DEL PAÍS VASCO ESCUELA TÉCNICA SUPERIOR DE A R Q U IT EC T U R A CENTRE D'INNOVATION MULTIDISCIPLINAIRE ÁRENNES UCC y A mis padres en especial, a mis hermanos, a mi novia y mis seres queridos, a mis amigos y compañeros, agradecido estoy por el cariño que me brindan siempre y el apoyo incondicional. A la Facultad de Arquitectura, y sus profesionales. GRACIAS TOTALES. ANÁLISIS / MEMORIA DESCRIPTIVA eman ta zabal zazu PROYECTOS VIII - EL ÁMBITO PÚBLICO II Profesor Titular: Arq. Juan José Segú Profesores Asociados: Arq. Iñigo García Odiaga Arq. Asier Acuriola Arq. Aritz Diez Oronoz San Sebastián, España 2019 DISEÑO ARQUITECTONICO V - DAV ucc Profesor Titular: Arq. José Ignacio Santillan Profesor Adjunto Arq. Esteban Barrera Jefe de Trabajos Prácticos: Arq. Juan Pablo Vázquez - - Centro de Innovación Multidisciplinar en Kennes Córdoba, Argentina 2020 C I M w ÍNDICE 01_ INTRODUCCIÓN / -

L'architecte Pierre Le Mousseux (1687
L’architecte Pierre Le Mousseux (1687 - 1740) : ses dernières années en Bourgogne L’architecte Pierre Le Mousseux (1687 - 1740) : ses dernières années en Bourgogne Brigitte Fromaget, ingénieur d'études. Inventaire. Région Bourgogne [email protected] Considéré avant tout comme un architecte d’exécution, Pierre Le Mousseux n’a fait l’objet d’aucune étude particulière. Sa vie et son œuvre ne sont connues que pendant ses périodes de collaboration avec les architectes du roi : de1716 à 1724, il est en Normandie où il bâtit pour le roi le haras du Pin sous la direction de Robert de Cotte, de 1725 à 1730, il est à Rennes car Jacques Gabriel l’a choisi comme adjoint pour la reconstruction de la ville et, en 1733, il arrive à Dijon où l’architecte du roi fait de nouveau appel à lui pour le seconder dans l’édification de l’escalier et d’une aile du palais des États. Seen primarily as an “execution” architect, Pierre Le Mousseux has never been studied as an individual creator. His life and his work are documented primarily during the periods when he collaborated with the King’s architects: from 1716 to 1724 when he was in Normandy and built the royal stud farm of Le Pin, under the direction of Robert de Cotte; and from 1725 to 1730 when he was at Rennes, under the direction of Jacques Gabriel for the reconstruction of the city. In 1733 he came to Dijon where the King’s architect again called on his assistance for the construction of a staircase and new wing of the States Palace.