Introduction to Physical Acoustics Class Webpage
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Acoustics & Ultrasonics
Dr.R.Vasuki Associate professor & Head Department of Physics Thiagarajar College of Engineering Madurai-625015 Science of sound that deals with origin, propagation and auditory sensation of sound. Sound production Propagation by human beings/machines Reception Classification of Sound waves Infrasonic audible ultrasonic Inaudible Inaudible < 20 Hz 20 Hz to 20,000 Hz ˃20,000 Hz Music – The sound which produces rhythmic sensation on the ears Noise-The sound which produces jarring & unpleasant effect To differentiate sound & noise Regularity of vibration Degree of damping Ability of ear to recognize the components Sound is a form of energy Sound is produced by the vibration of the body Sound requires a material medium for its propagation. When sound is conveyed from one medium to another medium there is no bodily motion of the medium Sound can be transmitted through solids, liquids and gases. Velocity of sound is higher in solids and lower in gases. Sound travels with velocity less than the velocity 8 of light. c= 3x 10 V0 =330 m/s at 0° degree Lightning comes first than thunder VT= V0+0.6 T Sound may be reflected, refracted or scattered. It undergoes diffraction and interference. Pitch or frequency Quality or timbre Intensity or Loudness Pitch is defined as the no of vibrations/sec. Frequency is a physical quantity but pitch is a physiological quantity. Mosquito- high pitch Lion- low pitch Quality or timbre is the one which helps to distinguish between the musical notes emitted by the different instruments or voices even though they have the same pitch. Intensity or loudness It is the average rate of flow of acoustic energy (Q) per unit area(A) situated normally to the direction of propagation of sound waves. -

Psychoacoustics Perception of Normal and Impaired Hearing with Audiology Applications Editor-In-Chief for Audiology Brad A
PSYCHOACOUSTICS Perception of Normal and Impaired Hearing with Audiology Applications Editor-in-Chief for Audiology Brad A. Stach, PhD PSYCHOACOUSTICS Perception of Normal and Impaired Hearing with Audiology Applications Jennifer J. Lentz, PhD 5521 Ruffin Road San Diego, CA 92123 e-mail: [email protected] Website: http://www.pluralpublishing.com Copyright © 2020 by Plural Publishing, Inc. Typeset in 11/13 Adobe Garamond by Flanagan’s Publishing Services, Inc. Printed in the United States of America by McNaughton & Gunn, Inc. All rights, including that of translation, reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, recording, or otherwise, including photocopying, recording, taping, Web distribution, or information storage and retrieval systems without the prior written consent of the publisher. For permission to use material from this text, contact us by Telephone: (866) 758-7251 Fax: (888) 758-7255 e-mail: [email protected] Every attempt has been made to contact the copyright holders for material originally printed in another source. If any have been inadvertently overlooked, the publishers will gladly make the necessary arrangements at the first opportunity. Library of Congress Cataloging-in-Publication Data Names: Lentz, Jennifer J., author. Title: Psychoacoustics : perception of normal and impaired hearing with audiology applications / Jennifer J. Lentz. Description: San Diego, CA : Plural Publishing, -

Investigation of the Time Dependent Nature of Infrasound Measured Near a Wind Farm Branko ZAJAMŠEK1; Kristy HANSEN1; Colin HANSEN1
Investigation of the time dependent nature of infrasound measured near a wind farm Branko ZAJAMŠEK1; Kristy HANSEN1; Colin HANSEN1 1 University of Adelaide, Australia ABSTRACT It is well-known that wind farm noise is dominated by low-frequency energy at large distances from the wind farm, where the high frequency noise has been more attenuated than low-frequency noise. It has also been found that wind farm noise is highly variable with time due to the influence of atmospheric factors such as atmospheric turbulence, wake turbulence from upstream turbines and wind shear, as well as effects that can be attributed to blade rotation. Nevertheless, many standards that are used to determine wind farm compliance are based on overall A-weighted levels which have been averaged over a period of time. Therefore the aim of the work described in this paper is to investigate the time dependent nature of unweighted wind farm noise and its perceptibility, with a focus on infrasound. Measurements were carried out during shutdown and operational conditions and results show that wind farm infrasound could be detectable by the human ear although not perceived as sound. Keywords: wind farm noise, on and off wind farm, infrasound, OHC threshold, crest factor I-INCE Classification of Subjects Number(s): 14.5.4 1. INTRODUCTION Wind turbine noise is influenced by atmospheric effects, which cause significant variations in the sound pressure level magnitude over time. In particular, factors causing amplitude variations include wind shear (1), directivity (2) and variations in the wind speed and direction. Wind shear, wind speed variations and yaw error (deviation of the turbine blade angle from optimum with respect to wind direction) cause changes in the blade loading and in the worst case, can lead to dynamic stall (3). -

The Physics of Sound 1
The Physics of Sound 1 The Physics of Sound Sound lies at the very center of speech communication. A sound wave is both the end product of the speech production mechanism and the primary source of raw material used by the listener to recover the speaker's message. Because of the central role played by sound in speech communication, it is important to have a good understanding of how sound is produced, modified, and measured. The purpose of this chapter will be to review some basic principles underlying the physics of sound, with a particular focus on two ideas that play an especially important role in both speech and hearing: the concept of the spectrum and acoustic filtering. The speech production mechanism is a kind of assembly line that operates by generating some relatively simple sounds consisting of various combinations of buzzes, hisses, and pops, and then filtering those sounds by making a number of fine adjustments to the tongue, lips, jaw, soft palate, and other articulators. We will also see that a crucial step at the receiving end occurs when the ear breaks this complex sound into its individual frequency components in much the same way that a prism breaks white light into components of different optical frequencies. Before getting into these ideas it is first necessary to cover the basic principles of vibration and sound propagation. Sound and Vibration A sound wave is an air pressure disturbance that results from vibration. The vibration can come from a tuning fork, a guitar string, the column of air in an organ pipe, the head (or rim) of a snare drum, steam escaping from a radiator, the reed on a clarinet, the diaphragm of a loudspeaker, the vocal cords, or virtually anything that vibrates in a frequency range that is audible to a listener (roughly 20 to 20,000 cycles per second for humans). -

Synchronization of a Thermoacoustic Oscillator by an External Sound Source G
Synchronization of a thermoacoustic oscillator by an external sound source G. Penelet and T. Biwa Citation: Am. J. Phys. 81, 290 (2013); doi: 10.1119/1.4776189 View online: http://dx.doi.org/10.1119/1.4776189 View Table of Contents: http://ajp.aapt.org/resource/1/AJPIAS/v81/i4 Published by the American Association of Physics Teachers Related Articles Reinventing the wheel: The chaotic sandwheel Am. J. Phys. 81, 127 (2013) Chaos: The Science of Predictable Random Motion. Am. J. Phys. 80, 843 (2012) Cavity quantum electrodynamics of a two-level atom with modulated fields Am. J. Phys. 80, 612 (2012) Stretching and folding versus cutting and shuffling: An illustrated perspective on mixing and deformations of continua Am. J. Phys. 79, 359 (2011) Anti-Newtonian dynamics Am. J. Phys. 77, 783 (2009) Additional information on Am. J. Phys. Journal Homepage: http://ajp.aapt.org/ Journal Information: http://ajp.aapt.org/about/about_the_journal Top downloads: http://ajp.aapt.org/most_downloaded Information for Authors: http://ajp.dickinson.edu/Contributors/contGenInfo.html Downloaded 21 Mar 2013 to 130.34.95.66. Redistribution subject to AAPT license or copyright; see http://ajp.aapt.org/authors/copyright_permission Synchronization of a thermoacoustic oscillator by an external sound source G. Peneleta) LUNAM Universite, Universite du Maine, CNRS UMR 6613, Laboratoire d’Acoustique de l’Universitedu Maine, Avenue Olivier Messiaen, 72085 Le Mans Cedex 9, France T. Biwa Department of Mechanical Systems and Design, Tohoku University, 980-8579 Sendai, Japan (Received 23 July 2012; accepted 29 December 2012) Since the pioneering work of Christiaan Huygens on the sympathy of pendulum clocks, synchronization phenomena have been widely observed in nature and science. -

General Acoustics
General Acoustics Catherine POTEL, Michel BRUNEAU Université du Maine - Le Mans - France These slides may sometimes appear incoherent when they are not associated to oral comments. Slides based upon C. POTEL, M. BRUNEAU, Acoustique Générale - équations différentielles et intégrales, solutions en milieux fluide et solide, applications, Ed. Ellipse collection Technosup, 352 pages, ISBN 2-7298-2805-2, 2006 C. Potel, M. Bruneau, "Acoustique générale (...)", Ed. Ellipse, collection Technosup, ISBN 2-7298-2805-2, 2006 The world of acoustics SCIENCES OF THE EARTH AND OF ENGINEERING SCIENCES THE ATMOSPHERELES GRANDS DOMAINES DE L'ACOUSTIQUEmechanical companies, buildings, solid and fluid mechanical transportation (air, road, railway), seismology, geology, aircraft noise, engineering submarine communication, telecommunications, bathymetry, fishing,... nuclear,... chemical physics of the Earth engineering, and of the aero- materials and atmosphere seismic waves, acoustics, structures propagation vibro- imaging, in the atmosphere acoustics ultrasonic non destructive electrical evaluation and engineering, testing electronics oceanography Chapter 1 underwater sonorisation, civil engi- acoustics, fundamental electro-acoustics neering and sonar and applied architecture acoustics, building, rooms, medicine measurement, entertainment, auditoria, comfort bioacoustics, signal,... cells imaging musical acoustics, physiology Acoustics and its applications: hearing, instruments phonation psycho- communi- generalities acoustics cation musics psychology speech -

Psychoacoustics and Its Benefit for the Soundscape
ACTA ACUSTICA UNITED WITH ACUSTICA Vol. 92 (2006) 1 – 1 Psychoacoustics and its Benefit for the Soundscape Approach Klaus Genuit, André Fiebig HEAD acoustics GmbH, Ebertstr. 30a, 52134 Herzogenrath, Germany. [klaus.genuit][andre.fiebig]@head- acoustics.de Summary The increase of complaints about environmental noise shows the unchanged necessity of researching this subject. By only relying on sound pressure levels averaged over long time periods and by suppressing all aspects of quality, the specific acoustic properties of environmental noise situations cannot be identified. Because annoyance caused by environmental noise has a broader linkage with various acoustical properties such as frequency spectrum, duration, impulsive, tonal and low-frequency components, etc. than only with SPL [1]. In many cases these acoustical properties affect the quality of life. The human cognitive signal processing pays attention to further factors than only to the averaged intensity of the acoustical stimulus. Therefore, it appears inevitable to use further hearing-related parameters to improve the description and evaluation of environmental noise. A first step regarding the adequate description of environmental noise would be the extended application of existing measurement tools, as for example level meter with variable integration time and third octave analyzer, which offer valuable clues to disturbing patterns. Moreover, the use of psychoacoustics will allow the improved capturing of soundscape qualities. PACS no. 43.50.Qp, 43.50.Sr, 43.50.Rq 1. Introduction disturbances and unpleasantness of environmental noise, a negative feeling evoked by sound. However, annoyance is The meaning of soundscape is constantly transformed and sensitive to subjectivity, thus the social and cultural back- modified. -
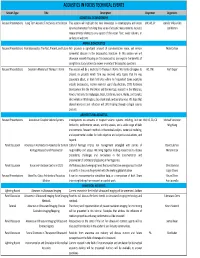
Acoustics in Focus Technical Events
ACOUSTICS IN FOCUS TECHNICAL EVENTS Session Type Title Description Cosponsor Organizers ACOUSTICAL OCEANOGRAPHY Focused Presentations Long Term Acoustic Time Series in the Ocean This session will highlight the new knowledge in oceanography and ocean UW, AB, SP Jennifer Miksis‐Olds dynamics harvested from long time series of acoustic measurements. Acoustic Joe Warren measurements relating to any aspect of the ocean floor, water column, or surface are welcome. ANIMAL BIOACOUSTICS Focused Presentations Fish Bioacoustics: The Past, Present, and Future Fish produce a significant amount of communicative noise, yet remain Nora Carlson somewhat obscure in the bioacoustics literature. In this session we will showcase research focusing on fish bioacoustics, and explore the benefits of using fish as study systems to answer a variety of bioacoustics questions. Focused Presentations Session in Memory of Thomas F. Norris This session will be a memorial to Thomas F. Norris. We invite colleagues to AO, UW Kerri Seger present on projects which Tom was involved with, topics that he was passionate about, or from field sites where he frequented. Some examples include bioacoustics, marine mammal signal classification, COTS hardware development like the MicroMars and Garmin tags, research in the Marianas, Hawaii, Vietnam, the Galapagos, Brazil, California, Guam, Alaska, and Canada; killer whales in Washington, ship shock trials, and aerial surveys. We hope that shared memories and reflection will offer healing through collegial science pursuits. ARCHITECTURAL ACOUSTICS Focused Presentations Acoustics in Coupled Volume Systems Investigations on acoustics in coupled volume systems including, but not MU, NS, SA, CA Michael Vorländer limited to, performance venues, worship spaces, and a wide range of built Ning Xiang environments. -

Acoustics: the Study of Sound Waves
Acoustics: the study of sound waves Sound is the phenomenon we experience when our ears are excited by vibrations in the gas that surrounds us. As an object vibrates, it sets the surrounding air in motion, sending alternating waves of compression and rarefaction radiating outward from the object. Sound information is transmitted by the amplitude and frequency of the vibrations, where amplitude is experienced as loudness and frequency as pitch. The familiar movement of an instrument string is a transverse wave, where the movement is perpendicular to the direction of travel (See Figure 1). Sound waves are longitudinal waves of compression and rarefaction in which the air molecules move back and forth parallel to the direction of wave travel centered on an average position, resulting in no net movement of the molecules. When these waves strike another object, they cause that object to vibrate by exerting a force on them. Examples of transverse waves: vibrating strings water surface waves electromagnetic waves seismic S waves Examples of longitudinal waves: waves in springs sound waves tsunami waves seismic P waves Figure 1: Transverse and longitudinal waves The forces that alternatively compress and stretch the spring are similar to the forces that propagate through the air as gas molecules bounce together. (Springs are even used to simulate reverberation, particularly in guitar amplifiers.) Air molecules are in constant motion as a result of the thermal energy we think of as heat. (Room temperature is hundreds of degrees above absolute zero, the temperature at which all motion stops.) At rest, there is an average distance between molecules although they are all actively bouncing off each other. -

Principles of Acoustics - Andres Porta Contreras, Catalina E
FUNDAMENTALS OF PHYSICS – Vol. I - Principles Of Acoustics - Andres Porta Contreras, Catalina E. Stern Forgach PRINCIPLES OF ACOUSTICS Andrés Porta Contreras Department of Physics, Universidad Nacional Autónoma de México, México Catalina E. Stern Forgach Department of Physics, Universidad Nacional Autónoma de México, México Keywords: Acoustics, Ear, Diffraction, Doppler effect, Music, Sound, Standing Waves, Ultrasound, Vibration, Waves. Contents 1. Introduction 2. History 3. Basic Concepts 3.1. What is Sound? 3.2. Characteristics of a Wave 3.3. Qualities of Sound 3.3.1. Loudness 3.3.2. Pitch 3.3.3. Timbre 3.4. Mathematical Description of a Pure Sound Wave 3.5. Doppler Effect 3.6. Reflection and Refraction 3.7. Superposition and Interference 3.8. Standing Waves 3.9. Timbre, Modes and Harmonics 3.10. Diffraction 4. Physiological and Psychological Effects of Sound 4.1. Anatomy and Physiology of Hearing. 4.1.1. Outer Ear 4.1.2. Middle Ear 4.1.3. Inner Ear 5. ApplicationsUNESCO – EOLSS 5.1. Ultrasound 5.2. Medicine 5.3. Noise Control 5.4. MeteorologySAMPLE and Seismology CHAPTERS 5.5. Harmonic Synthesis 5.6. Acoustical Architecture and Special Building Rooms Design 5.7. Speech and Voice 5.8. Recording and Reproduction 5.9. Other Glossary Bibliography Biographical Sketches ©Encyclopedia of Life Support Systems (EOLSS) FUNDAMENTALS OF PHYSICS – Vol. I - Principles Of Acoustics - Andres Porta Contreras, Catalina E. Stern Forgach Summary The chapter begins with a brief history of acoustics from Pythagoras to the present times. Then the main physical and mathematical principles on acoustics are reviewed. A general description of waves is given first, then the characteristics of sound and some of the most common phenomena related to acoustics like echo, diffraction and the Doppler effect are discussed. -

Chapter 12: Physics of Ultrasound
Chapter 12: Physics of Ultrasound Slide set of 54 slides based on the Chapter authored by J.C. Lacefield of the IAEA publication (ISBN 978-92-0-131010-1): Diagnostic Radiology Physics: A Handbook for Teachers and Students Objective: To familiarize students with Physics or Ultrasound, commonly used in diagnostic imaging modality. Slide set prepared by E.Okuno (S. Paulo, Brazil, Institute of Physics of S. Paulo University) IAEA International Atomic Energy Agency Chapter 12. TABLE OF CONTENTS 12.1. Introduction 12.2. Ultrasonic Plane Waves 12.3. Ultrasonic Properties of Biological Tissue 12.4. Ultrasonic Transduction 12.5. Doppler Physics 12.6. Biological Effects of Ultrasound IAEA Diagnostic Radiology Physics: a Handbook for Teachers and Students – chapter 12,2 12.1. INTRODUCTION • Ultrasound is the most commonly used diagnostic imaging modality, accounting for approximately 25% of all imaging examinations performed worldwide nowadays • Ultrasound is an acoustic wave with frequencies greater than the maximum frequency audible to humans, which is 20 kHz IAEA Diagnostic Radiology Physics: a Handbook for Teachers and Students – chapter 12,3 12.1. INTRODUCTION • Diagnostic imaging is generally performed using ultrasound in the frequency range from 2 to 15 MHz • The choice of frequency is dictated by a trade-off between spatial resolution and penetration depth, since higher frequency waves can be focused more tightly but are attenuated more rapidly by tissue The information in an ultrasonic image is influenced by the physical processes underlying propagation, reflection and attenuation of ultrasound waves in tissue IAEA Diagnostic Radiology Physics: a Handbook for Teachers and Students – chapter 12,4 12.1. -

Wind Farm Infrasound Detectability and Its Effects on the Percep- Tion of Wind Farm Noise Amplitude Modulation
Wind farm infrasound detectability and its effects on the percep- tion of wind farm noise amplitude modulation Duc Phuc Nguyen (1), Kristy Hansen (1), Branko Zajamsek (2), Gorica Micic (2) and Peter Catcheside (2) (1) College of Science and Engineering, Flinders University, Adelaide, Australia (2) Adelaide Institute for Sleep Health, Flinders University, Adelaide, Australia ABSTRACT Some residents attribute adverse effects to the presence of wind farm (WF) infrasound. However, dominant fea- tures of windfarm noise such as infrasound, tonality and amplitude modulation span the average human hearing threshold, so attribution to infrasound is problematic. This study used a combination of pre-recorded noise stimuli, measured at 3.2 km from a wind farm, in laboratory-based listening tests to investigate human perception of infrasound and amplitude modulation at realistic sound pressure levels in a group of 14 participants. Although a small sample size warrants cautious interpretation, preliminary results suggest differential effects between self- reported non-sensitive versus noise-sensitive participants, where the latter detected infrasound above chance. Infrasound did not affect the perception of amplitude modulation. Larger studies remain needed to clarify these findings. 1 INTRODUCTION Wind farm (WF) infrasound remains controversial and the source of substantial debate regarding potential effects of wind farm noise (WFN) on human health. The main infrasonic components of WFN can be measured many kilometres away from a wind farm, but typically at levels deemed well below the normal hearing threshold (Zajamšek et al. 2016, Turnbull, Turner, and Walsh 2012, Jakobsen 2005). The evidence for infrasound-specific effects on human health is very poor. A key hypothesis that has been advanced to explain wind farm noise related complaints, and partly supported by animal studies, suggesting that WF infrasound could potentially be detected by the ear, yet not heard, although supporting evidence from human studies remain lacking (Salt and Hullar 2010).