DOCSLIB.ORG

Circulatory Mechanics in the Toad Bufo Marinus I

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Circulatory Mechanics in the Toad Bufo Marinus I /. exp Biol. 158, 275-289 (1991) 275 Printed in Great Britain © The Company of Biologists Limited 1991 CIRCULATORY MECHANICS IN THE TOAD BUFO MARINUS I. STRUCTURE AND MECHANICAL DESIGN OF THE AORTA BY CAROL A. GIBBONS1 AND ROBERT E. SHADWICK2* 1 Department of Biology, University of Calgary, Calgary, Alberta, Canada, T2N1N4 and 2Marine Biology Research Division A-004, Scripps Institution of Oceanography, La Jolla, CA 92093, USA Accepted 28 March 1991 Summary This study describes several important mechanical design features of the aorta of a typical poikilothermic vertebrate. A strong functional similarity to the aorta of mammals is apparent, but some structural and mechanical differences are seen that reflect the lower pressure and simpler haemodynamics of the poikilothermic circulation. 1. The aorta is highly distensible, resilient and non-linearly elastic, giving it the requisite properties to act as an effective storage element in the arterial circulation. 2. An abrupt transition from high compliance (low elastic modulus) to relatively low compliance (high elastic modulus) takes place at pressures above the resting physiological range of 2-4 kPa. This behaviour reflects the composite nature of the artery wall in which rubbery elastin fibres and relatively rigid collagen fibres are the predominant elements. 3. The longitudinal tethering of the aorta when inflated is due primarily to anisotropy in elastic properties, rather than to links to the axial skeleton by branch vessels or connective tissue. 4. No significant changes in elastic properties or connective tissue content occur along the length of the toad arterial tree, in contrast to the situation in mammals. Introduction The aorta is an important elastic element in the arterial circulation. The vessel wall expands during systole and recoils during diastole, thereby storing and releasing elastic strain energy and smoothing the pulsatile output of the heart. An important benefit is the reduction of the arterial pressure pulse and, consequently, protection of the small exchange vessels from the high shear forces associated with pulsatile flow, and a reduction of the total energy required to circulate the blood (Taylor, 1964). To perform this function effectively, the aorta must have non- *To whom reprint requests should be addressed, rftey words: aorta, elasticity, circulatory system, mechanical design, Bufo marinus. 276 C. A. GIBBONS AND R. E. SHADWICK linear elastic properties in order to be a compliant reservoir at low pressures but be stiff enough to resist rupture at high pressures. Most of our information on structure and mechanical properties of arteries comes from studies on mammalian tissues (Bergel, 1961; Milnor, 1982). The artery wall is a composite structure whose non-linear elastic properties result from the combination of rubber-like elastic and relatively inextensible collagen fibres. The transition from a highly compliant to a relatively stiff vessel takes place at about 10-12 kPa, the mean resting blood pressure. In mammals, the distensibility of the aorta decreases as the ratio of collagen to elastin increases along the arterial tree. The elastic properties of the artery wall are important in determining the haemodynamic behaviour of the arterial system. Poikilothermic vertebrates generally have much lower blood pressures and often lower heart rates than do mammals (Shelton and Jones, 1968; Jones et al. 191 A; Shelton and Burggren, 1976; Langille and Jones, 1977). Nevertheless, the aortas of reptiles, amphibians and fish appear to have non-linear elastic properties (Goto and Kimoto, 1966; Satchell, 1971; Gibbons and Shadwick, 1989) that are comparable to those observed in mammals, but presumably appropriate for function in a lower-pressure system. However, very little is known about the relationship between structure, connective tissue composition and the elastic properties of the aorta in any lower vertebrate species. The purpose of this investigation is to make a detailed study of the aortic mechanical properties and their structural basis in the toad Bufo marinus, and to compare the design features of this arterial system to that of mammals. In a subsequent study (Gibbons and Shadwick, 1991), the effects of arterial elasticity on haemodynamic properties in the toad will be examined. Materials and methods Animals The experiments were performed on the toad, Bufo marinus L. Animals weighing 200-500 g were maintained in tanks at room temperature with access to water. They were fed mealworms weekly. The animals were killed by injection of MS-222 into the peritoneal cavity (Sandoz, 1:1000, 0.022 ml g~x body mass). The heart, aortic arches and dorsal aorta were exposed by a ventral midline incision. Four regions were arbitrarily designated, as shown in Fig. 1, and their in situ lengths determined before excision of the whole vessel. Experiments were performed on these aortic segments at room temperature within a few hours of death. Mechanical testing Artery segments (about 5 cm long) were placed in a chamber containing amphibian saline, and cannulated at one end with a blunt 18-gauge syringe needle and connectors leading to a pressure reservoir and a variable-speed pump. Once the air bubbles had been cleared, the distal end and the branch segments wei^ Mechanics of the toad aorta 277 Subclavian artery Site II Coeliacomesenteric artery Site III Site IV Sciatic artery Fig. 1. Diagram of the aorta and associated branches in the toad, Bufo marinus, approximately to scale. Four testing sites were used and are labelled as shown. Site I is the proximal aortic arch, from the branching of the truncus arteriosus to the subclavian artery. Site II is the distal aortic arch, between the subclavian artery and the coeliacomesenteric artery. Site in is the proximal dorsal aorta, from the coeliaco- mesenteric artery to the urogenital arteries. Site IV is the distal dorsal aorta, between the urogenital arteries and the sciatic arteries. The distance from the beginning of the systemic arch to the sciatic artery in a 350g animal is approximately 11 cm. ligated, and the vessel was extended to its in vivo length. The preparations were generally leak-free. Slow inflation-deflation cycles (lasting 1-2 min) were per- formed using a variable-speed pump. Conditioning cycles (usually 2-3) were run until the pressure-diameter curves were stable. The pressure during one cycle was raised to approximately lOkPa and lowered back to zero. Pressure was measured continuously using a P23Db Gould pressure transducer, while diameter was determined simultaneously with a video dimension analyzer system or VDA (Instrumentation for Physiology and Medicine, model 303), as described by Fung (1981). Some inflation tests were also performed on untethered vessel segments to measure the effect of increasing pressure on longitudinal extension. In this case, lengths were measured for step-wise pressure increments by using a microscope digital micrometer (Wild-Leitz MMS235). Pressure and radius data were collected on-line by a PDP11/23 laboratory computer (Digital Equipment Corporation) for the inflation-deflation cycles at four positions along the vessel from the arches to the sciatic arteries (Fig. 1). Values for radius at zero pressure were taken when the artery was stretched and it was unstretched. Frozen-cut sections were made of each vessel segment 278 C. A. GIBBONS AND R. E. SHADWICK after the inflation tests. From these, wall thickness and internal radius for the unstretched, unpressurized condition were measured using the digital micrometer. Assuming that the vessel wall is a constant-volume material, the internal radius and wall thickness could then be calculated at each pressure from the measured external radius and length. With these values, the luminal volume and circumfer- ential stress, strain and elastic modulus were calculated at 0.5 kPa intervals for each cycle and position, using the laboratory computer. Circumferential wall stress was defined as: a = Pr/h, (1) where r is the inside radius, h is the wall thickness and P is the pressure. The circumferential strain was calculated at mid-wall radius as: e = AR/Ro , (2) where R=(R+r)/2, R is the outer wall radius and Ro is the unstressed mid-wall radius. The elastic modulus describes the relationship between stress and strain and is a measure of material stiffness. For non-linear materials, such as the artery wall, the modulus varies with the level of strain. We used an incremental formula to calculate the elastic modulus (E) from biaxial stress-strain data obtained at constant vessel length (Bergel, 1961; Dobrin, 1983): £ = (l-^)(l + e)(Aa/Ae), (3) where fj. is the Poisson ratio, assumed to be 0.5 (see Dobrin, 1983). This formula uses an incremental strain that is based on the average radius at each pressure increment, and is therefore equivalent to e/(l + e) (Shadwick and Gosline, 1985). Pressure-strain, stress-strain and modulus-pressure relationships for each aortic position were calculated as mean curves from data pooled from several animals. Standard errors were calculated, and the mean curves were compared at each 0.5 kPa interval using multiple comparison tests to determine whether they differed significantly (Zar, 1984). Uniaxial force-extension tests were made on a tensile testing machine (Mon- santo Tensometer T10) in both the circumferential and longitudinal directions. For the circumferential testing, arterial rings were cut with 2 mm widths. They were placed around two metal L-shaped hooks. One hook was anchored at the base, while the other was connected to the force transducer attached to the moveable head. Longitudinal testing was done on vessel segments (2-3 cm long) held in vice- type clamps in the tensometer. Stress was then calculated as o=F/A, where F is the tensile force applied and A is the tissue cross-sectional area perpendicular to the force. Length changes (AL) were measured between surface markers by the video dimension analyzer. The markers were placed in the central region of the specimen to avoid any clamp effects.
Load more

Recommended publications
  • Evaluation of Artery Visualizations for Heart Disease Diagnosis
    Evaluation of Artery Visualizations for Heart Disease Diagnosis Michelle A. Borkin, Student Member, IEEE, Krzysztof Z. Gajos, Amanda Peters, Dimitrios Mitsouras, Simone Melchionna, Frank J. Rybicki, Charles L. Feldman, and Hanspeter Pfister, Senior Member, IEEE Fig. 1. Left: Traditional 2D projection (A) of a single artery, and 3D representation (C) of a right coronary artery tree with a rainbow color map. Right: 2D tree diagram representation (B) and equivalent 3D representation (D) of a left coronary artery tree with a diverging color map. Abstract—Heart disease is the number one killer in the United States, and finding indicators of the disease at an early stage is critical for treatment and prevention. In this paper we evaluate visualization techniques that enable the diagnosis of coronary artery disease. A key physical quantity of medical interest is endothelial shear stress (ESS). Low ESS has been associated with sites of lesion formation and rapid progression of disease in the coronary arteries. Having effective visualizations of a patient’s ESS data is vital for the quick and thorough non-invasive evaluation by a cardiologist. We present a task taxonomy for hemodynamics based on a formative user study with domain experts. Based on the results of this study we developed HemoVis, an interactive visualization application for heart disease diagnosis that uses a novel 2D tree diagram representation of coronary artery trees. We present the results of a formal quantitative user study with domain experts that evaluates the effect of 2D versus 3D artery representations and of color maps on identifying regions of low ESS. We show statistically significant results demonstrating that our 2D visualizations are more accurate and efficient than 3D representations, and that a perceptually appropriate color map leads to fewer diagnostic mistakes than a rainbow color map.
    [Show full text]
  • Ipsilateral Subclavian Steal in Association with Aberrant Origin of the Left Vertebral Artery from the Aortic Arch
    411 Ipsilateral Subclavian Steal in Association with Aberrant Origin of the Left Vertebral Artery from the Aortic Arch John Holder1 Five cases are reported of left subclavian steal syndrome associated with anomalous Eugene F. Binet2 origin of the left vertebral artery from the aortic arch. In all five instances blood flow at Bernard Thompson3 the origin of the left vertebral artery was in an antegrade direction contrary to that usually reported in this condition. The distal subclavian artery was supplied via an extensive collateral network of vessels connecting the vertebral artery to the thyro­ cervical trunk. If a significant stenosis or occlusion is present within the left subc lavi an artery proximal to the origin of the left vertebral artery, the direction of the bl ood fl ow within the vertebral artery will reverse toward the parent vessel (retrograde flow). This phenomenon occurs when a negative pressure gradient of 20-40 torr exists between the vertebral-basilar artery junction and th e vertebral-subc lavian artery junction [1-3]. We describe five cases of subclavian steal confirmed by angiography where a significant stenosis or occlusion of the left subclavian artery was demonstrated in association with anomalous origin of th e left vertebral artery directly from the aortic arch. In all five cases blood flow at the origin of the left vertebral artery was in an antegrade direction contrary to that more commonly reported in the subclavian steal syndrome. Materials and Methods The five patients were all 44- 58-year-old men. Three sought medical attention for symptoms specificall y related to th e left arm .
    [Show full text]
  • Vessels and Circulation
    CARDIOVASCULAR SYSTEM OUTLINE 23.1 Anatomy of Blood Vessels 684 23.1a Blood Vessel Tunics 684 23.1b Arteries 685 23.1c Capillaries 688 23 23.1d Veins 689 23.2 Blood Pressure 691 23.3 Systemic Circulation 692 Vessels and 23.3a General Arterial Flow Out of the Heart 693 23.3b General Venous Return to the Heart 693 23.3c Blood Flow Through the Head and Neck 693 23.3d Blood Flow Through the Thoracic and Abdominal Walls 697 23.3e Blood Flow Through the Thoracic Organs 700 Circulation 23.3f Blood Flow Through the Gastrointestinal Tract 701 23.3g Blood Flow Through the Posterior Abdominal Organs, Pelvis, and Perineum 705 23.3h Blood Flow Through the Upper Limb 705 23.3i Blood Flow Through the Lower Limb 709 23.4 Pulmonary Circulation 712 23.5 Review of Heart, Systemic, and Pulmonary Circulation 714 23.6 Aging and the Cardiovascular System 715 23.7 Blood Vessel Development 716 23.7a Artery Development 716 23.7b Vein Development 717 23.7c Comparison of Fetal and Postnatal Circulation 718 MODULE 9: CARDIOVASCULAR SYSTEM mck78097_ch23_683-723.indd 683 2/14/11 4:31 PM 684 Chapter Twenty-Three Vessels and Circulation lood vessels are analogous to highways—they are an efficient larger as they merge and come closer to the heart. The site where B mode of transport for oxygen, carbon dioxide, nutrients, hor- two or more arteries (or two or more veins) converge to supply the mones, and waste products to and from body tissues. The heart is same body region is called an anastomosis (ă-nas ′tō -mō′ sis; pl., the mechanical pump that propels the blood through the vessels.
    [Show full text]
  • The Variations of the Subclavian Artery and Its Branches Ahmet H
    Okajimas Folia Anat. Jpn., 76(5): 255-262, December, 1999 The Variations of the Subclavian Artery and Its Branches By Ahmet H. YUCEL, Emine KIZILKANAT and CengizO. OZDEMIR Department of Anatomy, Faculty of Medicine, Cukurova University, 01330 Balcali, Adana Turkey -Received for Publication, June 19,1999- Key Words: Subclavian artery, Vertebral artery, Arterial variation Summary: This study reports important variations in branches of the subclavian artery in a singular cadaver. The origin of the left vertebral artery was from the aortic arch. On the right side, no thyrocervical trunk was found. The two branches which normally originate from the thyrocervical trunk had a different origin. The transverse cervical artery arose directly from the subclavian artery and suprascapular artery originated from the internal thoracic artery. This variation provides a short route for posterior scapular anastomoses. An awareness of this rare variation is important because this area is used for diagnostic and surgical procedures. The subclavian artery, the main artery of the The variations of the subclavian artery and its upper extremity, also gives off the branches which branches have a great importance both in blood supply the neck region. The right subclavian arises vessels surgery and in angiographic investigations. from the brachiocephalic trunk, the left from the aortic arch. Because of this, the first part of the right and left subclavian arteries differs both in the Subjects origin and length. The branches of the subclavian artery are vertebral artery, internal thoracic artery, This work is based on a dissection carried out in thyrocervical trunk, costocervical trunk and dorsal the Department of Anatomy in the Faculty of scapular artery.
    [Show full text]
  • The Vertebral Artery in the Vascular Lab: What Does It Mean?
    The Vertebral Artery in the Vascular Lab: What Does It Mean? Caron Rockman MD Frances and Joseph Ritroto Professor of Surgery Program Director, Vascular Surgery New York University Langone Medical Center Disclosures •None Division of Vascular and Endovascular Surgery Subclavian Steal Occlusion of proximal Subclavian Art Vertebral artery supplies retrograde flow Posterior brain receives decreased flow 55 years + Men > Women more than 2:1 LSA affected 3x more than RSA Division of Vascular and Endovascular Surgery Subclavian Steal Causes: - Arteriosclerosis of subclavian artery (>95% cases) - Embolism - Takayasu’s Arteritis -Dissecting Aneurysm Risk Factors: (similar to CAD) -Smoking -Hypertension -Hyperlipidemia -Hypertension Division of Vascular and Endovascular Surgery Symptoms of Subclavian Steal Vertebrobasilar Insufficiency (posterior circulation symptoms) Light headedness or dizziness Ataxia or Vertigo Visual Disturbance Headache Syncope Confusion Division of Vascular and Endovascular Surgery Symptoms of Subclavian Steal Subclavian Insufficiency Arm weakness, coldness Numbness or “tingling” Arm Claudication with exercise Symptoms can be exacerbated with: Vigorous exercise Sudden turning of head to affected side Division of Vascular and Endovascular Surgery Signs of Subclavian Steal Diminished pulses (radial/ulnar) Discrepant blood pressures in upper extremities (>20mmHg) (Pitfall with bilateral disease) Subclavian Bruit 7 Division of Vascular and Endovascular Surgery Subclavian steal on Duplex Exam Incomplete steal •Striking deceleration of velocity in mid or late systole •High grade stenosis of subclavian rather than occlusion Complete Steal •Complete reversal of flow within the vertebral artery Division of Vascular and Endovascular Surgery Vertebral Retrograde Flow • Reversal of flow in the vertebral artery is a common finding identified on cerebrovascular duplex ultrasound. • The clinical significance and natural history of patients presenting with this finding, however, is poorly understood.
    [Show full text]
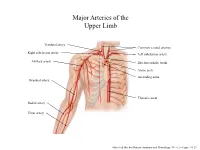
  • Major Arteries of the Upper Limb
    Major Arteries of the Upper Limb Vertebral artery Common carotid arteries Right subclavian artery Left subclavian artery Axillary artery Brachiocephalic trunk Aortic arch Ascending aorta Brachial artery Thoracic aorta Radial artery Ulnar artery Marieb & Hoehn (Human Anatomy and Physiology, 9th ed.) – Figure 19.23 Major Arteries of the Abdominal Region Renal artery Celiac trunk Abdominal aorta Superior mesenteric artery Gonadal artery Inferior mesenteric artery Common iliac artery Marieb & Hoehn (Human Anatomy and Physiology, 9th ed.) – Figure 19.24 Common iliac artery Internal iliac artery Major Arteries of the External iliac artery Lower Limb Femoral artery Popliteal artery Anterior tibial artery Fibular artery Posterior tibial artery Marieb & Hoehn (Human Anatomy and Physiology, 9th ed.) – Figure 19.25 Major Veins of the Upper Limb Internal jugular vein (left) Subclavian vein (right) External jugular vein (left) Axillary vein Brachiocephalic veins Cephalic vein Superior vena cava Brachial vein Basilic vein Median cubital vein Inferior vena cava Radial vein Ulnar vein Marieb & Hoehn (Human Anatomy and Physiology, 9th ed.) – Figure 19.28 Major Veins of the Abdominal Cavity – Part 1 Hepatic veins Inferior vena cava Renal vein (left) Gonadal vein (left) Gonadal vein (right) Common iliac vein (left) Marieb & Hoehn (Human Anatomy and Physiology, 9th ed.) – Figure 19.29 Major Veins of the Abdominal Cavity – Part 2 (Hepatic portal circulation) Hepatic portal vein Splenic vein Inferior mesenteric vein Superior mesenteric vein Marieb & Hoehn (Human Anatomy and Physiology, 9th ed.) – Figure 19.29 Common iliac vein (left) Internal iliac vein Major Veins of the External iliac vein Lower Limb Great saphenous vein Femoral vein Popliteal vein Fibular vein Small saphenous vein Anterior tibial Posterior tibial vein vein Marieb & Hoehn (Human Anatomy and Physiology, 9th ed.) – Figure 19.30 .
    [Show full text]
  • An Unusual Origin and Course of the Thyroidea Ima Artery, with Absence of Inferior Thyroid Artery Bilaterally
    Surgical and Radiologic Anatomy (2019) 41:235–237 https://doi.org/10.1007/s00276-018-2122-1 ANATOMIC VARIATIONS An unusual origin and course of the thyroidea ima artery, with absence of inferior thyroid artery bilaterally Doris George Yohannan1 · Rajeev Rajan1 · Akhil Bhuvanendran Chandran1 · Renuka Krishnapillai1 Received: 31 May 2018 / Accepted: 21 October 2018 / Published online: 25 October 2018 © Springer-Verlag France SAS, part of Springer Nature 2018 Abstract We report an unusual origin and course of the thyroidea ima artery in a male cadaver. The ima artery originated from the right subclavian artery very close to origin of the right vertebral artery. The artery coursed anteriorly between the common carotid artery medially and internal jugular vein laterally. It then coursed obliquely, from below upwards, from lateral to medial superficial to common carotid artery, to reach the inferior pole of the right lobe of thyroid and branched repeatedly to supply the anteroinferior and posteroinferior aspects of both the thyroid lobes and isthmus. The superior thyroid arteries were normal. Both the inferior thyroid arteries were absent. The unusual feature of this thyroidea ima artery is its origin from the subclavian artery close to vertebral artery origin, the location being remarkably far-off from the usual near midline position, and the oblique and relatively superficial course. This report is a caveat to neck surgeons to consider such a superficially running vessel to be a thyroidea ima artery. Keywords Thyroid vascular anatomy · Thyroidea ima artery · Artery of Neubauer · Blood supply of thyroid · Variations Introduction (1.1%), transverse scapular (1.1%), or pericardiophrenic or thyrocervical trunk [8, 10].
    [Show full text]
  • Arterial Variations of the Subclavian-Axillary Arterial Tree: Its Association with the Supply of the Rotator Cuff Muscles
    Int. J. Morphol., 32(4):1436-1443, 2014. Arterial Variations of the Subclavian-Axillary Arterial Tree: Its Association with the Supply of the Rotator Cuff Muscles Variaciones Arteriales del Árbol Arterial Subclavio-Axilar. Su Asociación con la Irrigación del Manguito de los Rotadores N. Naidoo*; L. Lazarus*; B. Z. De Gama*; N. O. Ajayi* & K. S. Satyapal* NAIDOO, N.; LAZARUS, L.; DE GAMA, B. Z.; AJAYI, N. O. & SATYAPAL, K. S. Arterial variations of the subclavian-axillary arterial tree: Its association with the supply of the rotator cuff muscles. Int. J. Morphol., 32(4):1436-1443, 2014. SUMMARY: The subclavian-axillary arterial tree is responsible for the arterial supply to the rotator cuff muscles as well as other shoulder muscles. This study comprised the bilateral dissection of the shoulder and upper arm region in thirty-one adult and nineteen fetal cadaveric specimens. The variable origins and branching patterns of the axillary, subscapular, circumflex scapular, thoracodorsal, posterior circumflex humeral and suprascapular arteries identified in this study corroborated the findings of previous studies. In addition, unique variations that are unreported in the literature were also observed. The precise anatomy of the arterial distribution to the rotator cuff muscles is important to the surgeon and radiologist. It will aid proper interpretation of radiographic images and avoid injury to this area during surgical procedures. KEY WORDS: Subclavian-axillary arterial tree; Variations; Supply; Rotator cuff muscles. INTRODUCTION Standard anatomical textbooks divide the axillary identified by Saralaya et al. (2008) to arise as a large artery into three parts using its relation to the pectoralis minor collateral branch from the first part of the axillary artery muscle (Salopek et al., 2007).
    [Show full text]
  • Journal of Neurology Research Review & Reports
    Journal of Neurology Research Review & Reports Case Report Open Access Bilateral Tortuous Upper Limb Arterial Tree and Their Clinical Significance Alka Bhingardeo Department of Anatomy, All India Institute of Medical Sciences, Bibinagar ABSTRACT The detailed knowledge about the possible anatomical variations of upper limb arteries is vital for the reparative surgery of the region. Brachial artery is the main artery of upper limb; it is a continuation of axillary artery from the lower border of teres major muscle. During routine cadaveric dissection, we found bilateral tortuous brachial artery which was superficial as well as tortuous throughout its course. It is called superficial as it was superficial to the median nerve. At the neck of radius, it was divided into two terminal branches radial and ulnar arteries which were also tortuous. Tortuosity of the radial artery was more near the flexor retinaculum. When observed, the continuation of ulnar artery as superficial palmar arch also showed tortuosity throughout, including its branches. Being superficial such brachial artery can be more prone to trauma. Tortuous radial artery is one of the causes of access failure in trans-radial approach of coronary interventions. To the best of our knowledge, this is the first case where entire post axillary upper limb arterial system is tortuous bilaterally. So knowledge of such tortuous upper limb arterial tree is important for cardiologist, radiologist, plastic surgeons and orthopedic surgeons. *Corresponding author Alka Bhingardeo, Assistant Professor, Department of Anatomy, All India Institute of Medical Sciences, Bibinagar, Telangana, India, Mob: 8080096151, Email: [email protected] Received: November 08, 2020; Accepted: November 16, 2020; Published: November 21, 2020 Keywords: Radial Artery, Superficial Brachial Artery, Tortuous, Brachial Artery Ulnar Artery, Upper Limb The brachial artery commenced from the axillary artery at the lower border of teres major muscle.
    [Show full text]
  • The Dorsal Scapular Artery - a Proposed Term for the Artery to the Rhomboid Muscles
    The Dorsal Scapular Artery - A Proposed Term for the Artery to the Rhomboid Muscles DONALD F. HUELKE Department of Anatomy, The University of Michigan, Medical School, Ann Arbor, Michigan The terminology of the arterial supply from the thyrocervical trunk in 77.5% of to the rhomboid and trapezius muscles is sides). (2) That the artery which sup- quite confusing in that each artery has plies the rhomboid muscles take the name been given two different names; names of the nerve along with which it passes, which are related to the variations in the and be designated the dorsal scapular ar- origin of these vessels. According to the tery. This artery arises from the second recent Paris Revision of the terminology or third part of the subclavian artery, sepa- (’55) one of these is the transverse cer- rate from the transverse cervical artery, vical artery, of the thyrocervical trunk, in approximately 70% of the sides. Thus, which gives rise to a superficial and a only one term is used for each artery. deep branch to the trapezius and rhom- If this modification in terminology is to boid muscles respectively. When these be accepted internationally, there must be branches arise separately, the trapezial an agreement among anatomists as to its branch is called the “superficial cervical “usual” site of origin. Only by comparing artery” and that to the rhomboids, the data on the origins of these arteries from “descending scapular artery.” Thus, each various countries can this end be achieved. vessel has two different names. Generally, Therefore, it is the purpose of this report an artery is named by the area of supply, to compare the data on these vessels of irrespective of its origin or variations.
    [Show full text]
  • Collateral Circulation in Spinal Cord Injury: a Comprehensive Review
    Published online: 2020-09-29 THIEME Review Article 1 Collateral Circulation in Spinal Cord Injury: A Comprehensive Review Ezequiel Garcia-Ballestas1 B. V. Murlimanju2 Yeider A. Durango-Espinosa1 Andrei F. Joaquim3 Harold E. Vasquez4 Luis Rafael Moscote-Salazar5 Amit Agrawal6 1Faculty of Medicine, Center for Biomedical Research (CIB), Address for correspondence Luis Rafael Moscote-Salazar, MD, University of Cartagena, Cartagena, Colombia Neurosurgeon-Critical Care, Center for Biomedical Research (CIB), 2Department of Anatomy, Kasturba Medical College, Mangalore, Cartagena Neurotrauma Research Group, Faculty of Medicine, Manipal Academy of Higher Education, Manipal, Karnataka, India University of Cartagena, Calle de la Universidad, Cra. 6 #36-100, 3Neurosurgery Division, Cartagena de Indias, Bolivar Department of Cartagena, Bolívar 130001, Columbia Neurology, State University of Campinas, Campinas-Sao Paulo, Brazil (e-mail: [email protected]). 4Universidad del Sinu, Cartagena de Indias, Consejo Latinoamericano de Neurointensivismo (CLaNi), Cartagena de Indias, Colombia 5Neurosurgeon-Critical Care, Center for Biomedical Research (CIB), Cartagena Neurotrauma Research Group, Faculty of Medicine, University of Cartagena, Cartagena, Colombia 6Department of Neurosurgery, All India Institute of Medical Sciences, Bhopal, Madhya Pradesh, India Indian J Neurotrauma:2021;18:1–6 Abstract Surgery is the most common cause of spinal cord ischemia; it is also caused by hemo- dynamic changes, which disrupt the blood flow. Direct ligation of the spinal arteries, especially the Adamkiewicz artery is involved as well. Other causes of spinal cord isch- emia include arteriography procedures, thoracic surgery, epidural and rachianesthesia, foraminal infiltration, arterial dissection, systemic hypotension, emboligenic heart dis- ease, thoracic disc herniation, and compression. Understanding the vascular anatomy of the spinal cord is essential to develop optimal strategies for preventing ischemic injuries to the spinal cord.
    [Show full text]
  • Arterial Variations Within the Lateral Cervical Region: a Multidetector CT Angiography Study
    Int. J. Morphol., 37(3):991-996, 2019. Arterial Variations Within the Lateral Cervical Region: A Multidetector CT Angiography Study Variaciones Arteriales en la Región Cervical Lateral: Estudio Angiográfico por Tomografía Computarizada Multidetector Erdogan Bulbul1; Bahar Yanik1; Emrah Akay1; Vildan Koksal2 & Gulen Demirpolat1 BULBUL, E.; YANIK, B.; AKAY, E.; KOKSAL, V. & DEMIRPOLAT, G. Arterial variations within the lateral cervical region: A multidetector CT angiography study. Int. J. Morphol., 37(3):991-996, 2019. SUMMARY: It is important to know the arterial anatomy within the lateral cervical region before the flap-planning. We evaluated the arterial anatomy in this area using multidetector computed tomography (CT) angiography and our aim was to establish the arterial variations. Both sides of individuals in a total number of 155 carotid CT angiographies are reviewed by using 64-detector CT, retrospectively. The variations of suprascapular artery, superficial cervical artery, dorsal scapular artery that are inclusive of the lateral cervical region were assessed. Three arteries originated individually in 67 (23.8 %) sides. They arose by trunk formation in 214 (76.2 %) sides. The most common type of trunk formation was cervicodorsal trunk (107; 38 %). The others were cervicoscapular trunk, cervicodorsoscapular trunk, dorsoscapular trunk and detected in 66 (23.4 %), 40 (14.3 %), 1 (0.3 %) sides, respectively. The origins of arteries within the lateral cervical region may show variations and they may originate from subclavian artery or its branches individually or by trunk formations. It may be beneficial to know these variations before the reconstructive surgical procedures in head and neck. CT angiography is a non-invasive method that enables to evaluate the arterial anatomy and variations in this area.
    [Show full text]