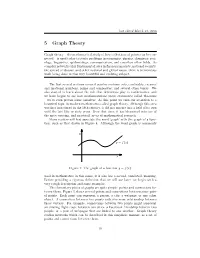
Graph of a function
Top View
- Introduction to Euler's Method
- Basic Calculus Refresher
- The Gradient 1. the Gradient of F : R 3 ↦→ R Is the Vector ∇F
- Chapter 5: Continuity of Functions
- The Derivative
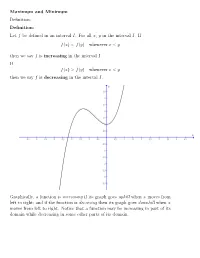
- Maxima and Minima
- The First and Second Derivatives the Meaning of the First Derivative at the End of the Last Lecture, We Knew How to Differentiate Any Polynomial Function
- Directional Derivatives and the Gradient Vector
- Chapter 1 Functions and Models
- Notes on Differential Equations Tom Duchamp November 20, 2019
- Antiderivatives Sometimes We Are Given a Function F(X)
- Finding Antiderivatives and Evaluating Integrals
- Painless, Highly Accurate Discretizations of the Laplacian on a Smooth Manifold
- 1 Computing a Tangent Line
- INTUITIVE INFINITESIMAL CALCULUS 7.1 Polar Coordinates
- Directional Derivatives, Steepest Ascent, Tangent Planes Math 131
- The Integral
- Functions and Their Graphs