Ellipticals with Kinematically--Distinct Cores: WFPC2 Imaging of Globular
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

X-Ray Luminosities for a Magnitude-Limited Sample of Early-Type Galaxies from the ROSAT All-Sky Survey
Mon. Not. R. Astron. Soc. 302, 209±221 (1999) X-ray luminosities for a magnitude-limited sample of early-type galaxies from the ROSAT All-Sky Survey J. Beuing,1* S. DoÈbereiner,2 H. BoÈhringer2 and R. Bender1 1UniversitaÈts-Sternwarte MuÈnchen, Scheinerstrasse 1, D-81679 MuÈnchen, Germany 2Max-Planck-Institut fuÈr Extraterrestrische Physik, D-85740 Garching bei MuÈnchen, Germany Accepted 1998 August 3. Received 1998 June 1; in original form 1997 December 30 Downloaded from https://academic.oup.com/mnras/article/302/2/209/968033 by guest on 30 September 2021 ABSTRACT For a magnitude-limited optical sample (BT # 13:5 mag) of early-type galaxies, we have derived X-ray luminosities from the ROSATAll-Sky Survey. The results are 101 detections and 192 useful upper limits in the range from 1036 to 1044 erg s1. For most of the galaxies no X-ray data have been available until now. On the basis of this sample with its full sky coverage, we ®nd no galaxy with an unusually low ¯ux from discrete emitters. Below log LB < 9:2L( the X-ray emission is compatible with being entirely due to discrete sources. Above log LB < 11:2L( no galaxy with only discrete emission is found. We further con®rm earlier ®ndings that Lx is strongly correlated with LB. Over the entire data range the slope is found to be 2:23 60:12. We also ®nd a luminosity dependence of this correlation. Below 1 log Lx 40:5 erg s it is consistent with a slope of 1, as expected from discrete emission. -

7.5 X 11.5.Threelines.P65
Cambridge University Press 978-0-521-19267-5 - Observing and Cataloguing Nebulae and Star Clusters: From Herschel to Dreyer’s New General Catalogue Wolfgang Steinicke Index More information Name index The dates of birth and death, if available, for all 545 people (astronomers, telescope makers etc.) listed here are given. The data are mainly taken from the standard work Biographischer Index der Astronomie (Dick, Brüggenthies 2005). Some information has been added by the author (this especially concerns living twentieth-century astronomers). Members of the families of Dreyer, Lord Rosse and other astronomers (as mentioned in the text) are not listed. For obituaries see the references; compare also the compilations presented by Newcomb–Engelmann (Kempf 1911), Mädler (1873), Bode (1813) and Rudolf Wolf (1890). Markings: bold = portrait; underline = short biography. Abbe, Cleveland (1838–1916), 222–23, As-Sufi, Abd-al-Rahman (903–986), 164, 183, 229, 256, 271, 295, 338–42, 466 15–16, 167, 441–42, 446, 449–50, 455, 344, 346, 348, 360, 364, 367, 369, 393, Abell, George Ogden (1927–1983), 47, 475, 516 395, 395, 396–404, 406, 410, 415, 248 Austin, Edward P. (1843–1906), 6, 82, 423–24, 436, 441, 446, 448, 450, 455, Abbott, Francis Preserved (1799–1883), 335, 337, 446, 450 458–59, 461–63, 470, 477, 481, 483, 517–19 Auwers, Georg Friedrich Julius Arthur v. 505–11, 513–14, 517, 520, 526, 533, Abney, William (1843–1920), 360 (1838–1915), 7, 10, 12, 14–15, 26–27, 540–42, 548–61 Adams, John Couch (1819–1892), 122, 47, 50–51, 61, 65, 68–69, 88, 92–93, -

Pos(LCDU 2013)014
Properties of dust and PAHs in various environments of nearby galaxies PoS(LCDU 2013)014 Hidehiro Kaneda∗ Graduate School of Science, Nagoya University, Nagoya 464-8602, Japan E-mail: [email protected] In star-forming regions, dust and polycyclic aromatic hydrocarbons (PAHs) absorb a significant fraction of stellar ultraviolet (UV) photons and re-radiate them in the infrared (IR). Hence the IR luminosities due to dust and PAH emission are both powerful tools to trace star-forming activities in galaxies. However they are not merely tracers of star-formation activity. Spectral information on the dust and PAH emission would have much deeper physical implications for understanding the properties of the ISM. External galaxies provide us with a much wider range of the ISM physical conditions than our Galaxy. For example, Spitzer mid-IR spectroscopy has shown a variety of the PAH emission features for various types of galaxies, which reflects significant changes in the properties of PAHs, such as an ionization state and a size distribution. AKARI near-IR spectroscopy has revealed spatial variations in the intensity ratio of the aromatic to the aliphatic hydrocarbon spectral feature in galaxies, indicating structural changes of carbonaceous grains in shocked regions. The relation of PAH to far-IR dust is another important probe to study the conditions of the interstellar environments. In general, PAHs and far-IR dust are mixed well in the ISM, producing global correlations between their IR luminosities. In local areas within a galaxy, however, their abundance ratios are expected to vary substantially due to interactions with interstellar shocks, hard UV radiation fields and diffuse X-ray hot plasmas. -

Making a Sky Atlas
Appendix A Making a Sky Atlas Although a number of very advanced sky atlases are now available in print, none is likely to be ideal for any given task. Published atlases will probably have too few or too many guide stars, too few or too many deep-sky objects plotted in them, wrong- size charts, etc. I found that with MegaStar I could design and make, specifically for my survey, a “just right” personalized atlas. My atlas consists of 108 charts, each about twenty square degrees in size, with guide stars down to magnitude 8.9. I used only the northernmost 78 charts, since I observed the sky only down to –35°. On the charts I plotted only the objects I wanted to observe. In addition I made enlargements of small, overcrowded areas (“quad charts”) as well as separate large-scale charts for the Virgo Galaxy Cluster, the latter with guide stars down to magnitude 11.4. I put the charts in plastic sheet protectors in a three-ring binder, taking them out and plac- ing them on my telescope mount’s clipboard as needed. To find an object I would use the 35 mm finder (except in the Virgo Cluster, where I used the 60 mm as the finder) to point the ensemble of telescopes at the indicated spot among the guide stars. If the object was not seen in the 35 mm, as it usually was not, I would then look in the larger telescopes. If the object was not immediately visible even in the primary telescope – a not uncommon occur- rence due to inexact initial pointing – I would then scan around for it. -

Ngc Catalogue Ngc Catalogue
NGC CATALOGUE NGC CATALOGUE 1 NGC CATALOGUE Object # Common Name Type Constellation Magnitude RA Dec NGC 1 - Galaxy Pegasus 12.9 00:07:16 27:42:32 NGC 2 - Galaxy Pegasus 14.2 00:07:17 27:40:43 NGC 3 - Galaxy Pisces 13.3 00:07:17 08:18:05 NGC 4 - Galaxy Pisces 15.8 00:07:24 08:22:26 NGC 5 - Galaxy Andromeda 13.3 00:07:49 35:21:46 NGC 6 NGC 20 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 7 - Galaxy Sculptor 13.9 00:08:21 -29:54:59 NGC 8 - Double Star Pegasus - 00:08:45 23:50:19 NGC 9 - Galaxy Pegasus 13.5 00:08:54 23:49:04 NGC 10 - Galaxy Sculptor 12.5 00:08:34 -33:51:28 NGC 11 - Galaxy Andromeda 13.7 00:08:42 37:26:53 NGC 12 - Galaxy Pisces 13.1 00:08:45 04:36:44 NGC 13 - Galaxy Andromeda 13.2 00:08:48 33:25:59 NGC 14 - Galaxy Pegasus 12.1 00:08:46 15:48:57 NGC 15 - Galaxy Pegasus 13.8 00:09:02 21:37:30 NGC 16 - Galaxy Pegasus 12.0 00:09:04 27:43:48 NGC 17 NGC 34 Galaxy Cetus 14.4 00:11:07 -12:06:28 NGC 18 - Double Star Pegasus - 00:09:23 27:43:56 NGC 19 - Galaxy Andromeda 13.3 00:10:41 32:58:58 NGC 20 See NGC 6 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 21 NGC 29 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 22 - Galaxy Pegasus 13.6 00:09:48 27:49:58 NGC 23 - Galaxy Pegasus 12.0 00:09:53 25:55:26 NGC 24 - Galaxy Sculptor 11.6 00:09:56 -24:57:52 NGC 25 - Galaxy Phoenix 13.0 00:09:59 -57:01:13 NGC 26 - Galaxy Pegasus 12.9 00:10:26 25:49:56 NGC 27 - Galaxy Andromeda 13.5 00:10:33 28:59:49 NGC 28 - Galaxy Phoenix 13.8 00:10:25 -56:59:20 NGC 29 See NGC 21 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 30 - Double Star Pegasus - 00:10:51 21:58:39 -

II. the E-MERLIN Legacy Survey of Nearby Galaxies. the Deepest Radio View of the Palomar Sample on Parsec Scale R.D
LeMMINGs – II. The e-MERLIN legacy survey of nearby galaxies. The deepest radio view of the Palomar sample on parsec scale R.D. Baldi, D.R.A. Williams, I.M. Mchardy, R.J. Beswick, E. Brinks, B.T. Dullo, J.H. Knapen, M.K. Argo, S. Aalto, A. Alberdi, et al. To cite this version: R.D. Baldi, D.R.A. Williams, I.M. Mchardy, R.J. Beswick, E. Brinks, et al.. LeMMINGs – II. The e-MERLIN legacy survey of nearby galaxies. The deepest radio view of the Palomar sample on parsec scale. Monthly Notices of the Royal Astronomical Society, Oxford University Press (OUP): Policy P - Oxford Open Option A, 2020, 500 (4), pp.4749-4767. 10.1093/mnras/staa3519. hal-03022746 HAL Id: hal-03022746 https://hal.archives-ouvertes.fr/hal-03022746 Submitted on 22 Apr 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. MNRAS 500, 4749–4767 (2021) doi:10.1093/mnras/staa3519 Advance Access publication 2020 November 17 LeMMINGs – II. The e-MERLIN legacy survey of nearby galaxies. The deepest radio view of the Palomar sample on parsec scale R. D. -

A Classical Morphological Analysis of Galaxies in the Spitzer Survey Of
Accepted for publication in the Astrophysical Journal Supplement Series A Preprint typeset using LTEX style emulateapj v. 03/07/07 A CLASSICAL MORPHOLOGICAL ANALYSIS OF GALAXIES IN THE SPITZER SURVEY OF STELLAR STRUCTURE IN GALAXIES (S4G) Ronald J. Buta1, Kartik Sheth2, E. Athanassoula3, A. Bosma3, Johan H. Knapen4,5, Eija Laurikainen6,7, Heikki Salo6, Debra Elmegreen8, Luis C. Ho9,10,11, Dennis Zaritsky12, Helene Courtois13,14, Joannah L. Hinz12, Juan-Carlos Munoz-Mateos˜ 2,15, Taehyun Kim2,15,16, Michael W. Regan17, Dimitri A. Gadotti15, Armando Gil de Paz18, Jarkko Laine6, Kar´ın Menendez-Delmestre´ 19, Sebastien´ Comeron´ 6,7, Santiago Erroz Ferrer4,5, Mark Seibert20, Trisha Mizusawa2,21, Benne Holwerda22, Barry F. Madore20 Accepted for publication in the Astrophysical Journal Supplement Series ABSTRACT The Spitzer Survey of Stellar Structure in Galaxies (S4G) is the largest available database of deep, homogeneous middle-infrared (mid-IR) images of galaxies of all types. The survey, which includes 2352 nearby galaxies, reveals galaxy morphology only minimally affected by interstellar extinction. This paper presents an atlas and classifications of S4G galaxies in the Comprehensive de Vaucouleurs revised Hubble-Sandage (CVRHS) system. The CVRHS system follows the precepts of classical de Vaucouleurs (1959) morphology, modified to include recognition of other features such as inner, outer, and nuclear lenses, nuclear rings, bars, and disks, spheroidal galaxies, X patterns and box/peanut structures, OLR subclass outer rings and pseudorings, bar ansae and barlenses, parallel sequence late-types, thick disks, and embedded disks in 3D early-type systems. We show that our CVRHS classifications are internally consistent, and that nearly half of the S4G sample consists of extreme late-type systems (mostly bulgeless, pure disk galaxies) in the range Scd-Im. -
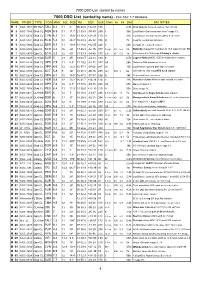
DSO List V2 Current
7000 DSO List (sorted by name) 7000 DSO List (sorted by name) - from SAC 7.7 database NAME OTHER TYPE CON MAG S.B. SIZE RA DEC U2K Class ns bs Dist SAC NOTES M 1 NGC 1952 SN Rem TAU 8.4 11 8' 05 34.5 +22 01 135 6.3k Crab Nebula; filaments;pulsar 16m;3C144 M 2 NGC 7089 Glob CL AQR 6.5 11 11.7' 21 33.5 -00 49 255 II 36k Lord Rosse-Dark area near core;* mags 13... M 3 NGC 5272 Glob CL CVN 6.3 11 18.6' 13 42.2 +28 23 110 VI 31k Lord Rosse-sev dark marks within 5' of center M 4 NGC 6121 Glob CL SCO 5.4 12 26.3' 16 23.6 -26 32 336 IX 7k Look for central bar structure M 5 NGC 5904 Glob CL SER 5.7 11 19.9' 15 18.6 +02 05 244 V 23k st mags 11...;superb cluster M 6 NGC 6405 Opn CL SCO 4.2 10 20' 17 40.3 -32 15 377 III 2 p 80 6.2 2k Butterfly cluster;51 members to 10.5 mag incl var* BM Sco M 7 NGC 6475 Opn CL SCO 3.3 12 80' 17 53.9 -34 48 377 II 2 r 80 5.6 1k 80 members to 10th mag; Ptolemy's cluster M 8 NGC 6523 CL+Neb SGR 5 13 45' 18 03.7 -24 23 339 E 6.5k Lagoon Nebula;NGC 6530 invl;dark lane crosses M 9 NGC 6333 Glob CL OPH 7.9 11 5.5' 17 19.2 -18 31 337 VIII 26k Dark neb B64 prominent to west M 10 NGC 6254 Glob CL OPH 6.6 12 12.2' 16 57.1 -04 06 247 VII 13k Lord Rosse reported dark lane in cluster M 11 NGC 6705 Opn CL SCT 5.8 9 14' 18 51.1 -06 16 295 I 2 r 500 8 6k 500 stars to 14th mag;Wild duck cluster M 12 NGC 6218 Glob CL OPH 6.1 12 14.5' 16 47.2 -01 57 246 IX 18k Somewhat loose structure M 13 NGC 6205 Glob CL HER 5.8 12 23.2' 16 41.7 +36 28 114 V 22k Hercules cluster;Messier said nebula, no stars M 14 NGC 6402 Glob CL OPH 7.6 12 6.7' 17 37.6 -03 15 248 VIII 27k Many vF stars 14.. -

The Host Galaxy/AGN Connection in Nearby Early-Type Galaxies
Astronomy & Astrophysics manuscript no. 3113 November 16, 2018 (DOI: will be inserted by hand later) The host galaxy/AGN connection in nearby early-type galaxies ⋆ Sample selection and hosts brightness profiles Alessandro Capetti1 and Barbara Balmaverde2 1 INAF - Osservatorio Astronomico di Torino, Strada Osservatorio 20, I-10025 Pino Torinese, Italy e-mail: [email protected] 2 Universit´adi Torino, Via Giuria 1, I-10125, Torino, Italy e-mail: [email protected] Abstract. This is the first of a series of three papers exploring the connection between the multiwavelength properties of AGNs in nearby early-type galaxies and the characteristics of their hosts. We selected two samples, both with high resolution 5 GHz VLA observations available and providing measurements down to 1 mJy level, − reaching radio-luminosities as low as 1019 W Hz 1. We focus on the 116 radio-detected galaxies as to boost the fraction of AGN with respect to a purely optically selected sample. Here we present the analysis of the optical brightness profiles based on archival HST images, available for 65 objects. We separate early-type galaxies on the basis of the slope of their nuclear brightness profiles, into core and power-law galaxies following the Nuker’s scheme, rather than on the traditional morphological classification (i.e. into E and S0 galaxies). Our sample of AGN candidates is indistinguishable, when their brightness profiles are concerned, from galaxies of similar optical luminosity but hosting weaker (or no) radio-sources. We confirm previous findings that relatively bright 21.5 −1 radio-sources (Lr > 10 W Hz ) are uniquely associated to core galaxies. -

Processing of Interstellar Dust Grains in Galaxies
Publications of the Korean Astronomical Society ISSN 1225-1534 (Print) 27: 237 » 242, 2012 September http://dx.doi.org/10.5303/PKAS.2012.27.4.237 °c 2012. The Korean Astronomical Society. All Rights Reserved. PROCESSING OF INTERSTELLAR DUST GRAINS IN GALAXIES H. Kaneda1, D. Ishihara1, T. Onaka2, I. Sakon2, T. Suzuki3, K. Kobata1, T. Kondo1, M. Yamagishi1, and A. Yasuda1 1Graduate School of Science, Nagoya University, Chikusa-ku, Nagoya 464-8602, Japan 2Department of Astronomy, Graduate School of Science, University of Tokyo, Bunkyo-ku, Tokyo 113-0033, Japan 3Institute of Space and Astronautical Science, Japan Aerospace Exploration Agency, Sagamihara, Kanagawa 252-5210, Japan E-mail: [email protected] (Received June 29, 2012; Accepted August 12, 2012) ABSTRACT We have performed a systematic study of interstellar dust grains in various environments of galaxies. AKARI has revealed the detailed properties of dust grains not only in star-forming regions but also in regions not relevant to star formation, some of which are found not to follow our old empirical knowledge. Because of its unique capabilities, AKARI has provided new knowledge on the processing of large grains and polycyclic aromatic hydrocarbons (PAHs). For example, we detect PAHs from elliptical galaxies, which show unusual spectral features and spatial distributions, demonstrating importance of material processing in the interstellar space. We find that copious amounts of large grains and PAHs are flowing out of starburst galaxies by galactic superwinds, which are being shattered and destroyed in galactic haloes. We discover evidence for graphitization of carbonaceous grains near the center of our Galaxy, providing a clue to understanding the activity of the Galactic center. -

Radio Sources in Low-Luminosity Active Galactic Nuclei
A&A 435, 521–543 (2005) Astronomy DOI: 10.1051/0004-6361:20042277 & c ESO 2005 Astrophysics Radio sources in low-luminosity active galactic nuclei IV. Radio luminosity function, importance of jet power, and radio properties of the complete Palomar sample N. M. Nagar1,2, H. Falcke3, and A. S. Wilson4 1 Kapteyn Institute, Landleven 12, 9747 AD Groningen, The Netherlands 2 Astronomy Group, Departamento de Física, Universidad de Concepción, Casilla 160-C, Concepción, Chile e-mail: [email protected] 3 ASTRON, PO Box 2, 7990 AA Dwingeloo, The Netherlands Department of Astronomy, Radboud University Nijmegen, Postbus 9010, 6500 GL Nijmegen, The Netherlands e-mail: [email protected] 4 Department of Astronomy, University of Maryland, College Park, MD 20742, USA Adjunct Astronomer, Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA e-mail: [email protected] Received 29 October 2004 / Accepted 5 February 2005 Abstract. We present the completed results of a high resolution radio imaging survey of all (∼200) low-luminosity active galactic nuclei (LLAGNs) and AGNs in the Palomar Spectroscopic Sample of all (∼488) bright northern galaxies. The high incidences of pc-scale radio nuclei, with implied brightness temperatures ∼>107 K, and sub-parsec jets argue for accreting black holes in ∼>50% of all LINERs and low-luminosity Seyferts; there is no evidence against all LLAGNs being mini-AGNs. The detected parsec-scale radio nuclei are preferentially found in massive ellipticals and in type 1 nuclei (i.e. nuclei with broad Hα emission). The radio luminosity function (RLF) of Palomar Sample LLAGNs and AGNs extends three orders of magnitude below, and is continuous with, that of “classical” AGNs. -
An X-Ray View of 82 Liners with Chandra and XMM-Newton Data O
CORE Metadata, citation and similar papers at core.ac.uk Provided by Digital.CSIC Astronomy & Astrophysics manuscript no. O.Gonzalez-Martin-LINERs˙xray c ESO 2009 May 13, 2009 An X-ray view of 82 LINERs with Chandra and XMM-Newton data O. Gonzalez-Mart´ ´ın1 ;?, J. Masegosa2, I. Marquez´ 2, M. Guainazzi3 and E. Jimenez-Bail´ on´ 4 1 X-ray Astronomy Group, Department of Physics and Astronomy, Leicester University, Leicester LE1 7RH, UK e-mail: [email protected] 2 Instituto de Astrof´ısica de Andaluc´ıa, CSIC, Granada, SPAIN 3 European Space Astronomy Centre of ESA, P.O. Box 78, Villanueva de la Canada, E-28691 Madrid, SPAIN 4 Instituto de Astronom´ıa, Universidad Nacional Autonoma´ de Mexico, Apartado Postal 70-264, 04510 Mexico DF, MEXICO ABSTRACT We present the results of an homogeneous X-ray analysis for 82 nearby LINERs selected from the catalogue of Carrillo et al. (1999). All sources have available Chandra (68 sources) and/or XMM-Newton (55 sources) observations. This is the largest sample of LINERs with X-ray spectral data (60 out of the 82 objects) and significantly improves our previous analysis based on Chandra data for 51 LINERs (Gonzalez-Martin et al. 2006). It increases both the sample size and adds XMM-Newton data. New models permit the inclusion of double absorbers in the spectral fits. Nuclear X-ray morphology is inferred from the compactness of detected nuclear sources in the hard band (4.5-8.0 keV). Sixty per cent of the sample shows a compact nuclear source and are classified as AGN candidates.